人教版数学九年级下册27.2.3相似三角形的性质(3)(共15张PPT)
文档属性
| 名称 | 人教版数学九年级下册27.2.3相似三角形的性质(3)(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
一、相似三角形的性质
①相似三角形的对应角相等,对应边成比例.
②相似三角形对应中线的比,对应角平分线的 比,对应高的比,对应周长的比都等于相似比.
③相似三角形面积的比等于相似比的平方.
二.相似三角形的判定方法
定理1 两角对应相等的两个三角形相似.
推论1 平行于三角形一边直线截其它两边(或其延长线),所截得的三角形与原三角形相似;
定理2 三边对应成比例的两个三角形相似.
定理3 两边对应成比例,且夹角相等的两个三角形相似;
定理4 斜边直角边对应成比例的两个直角三角形相似.
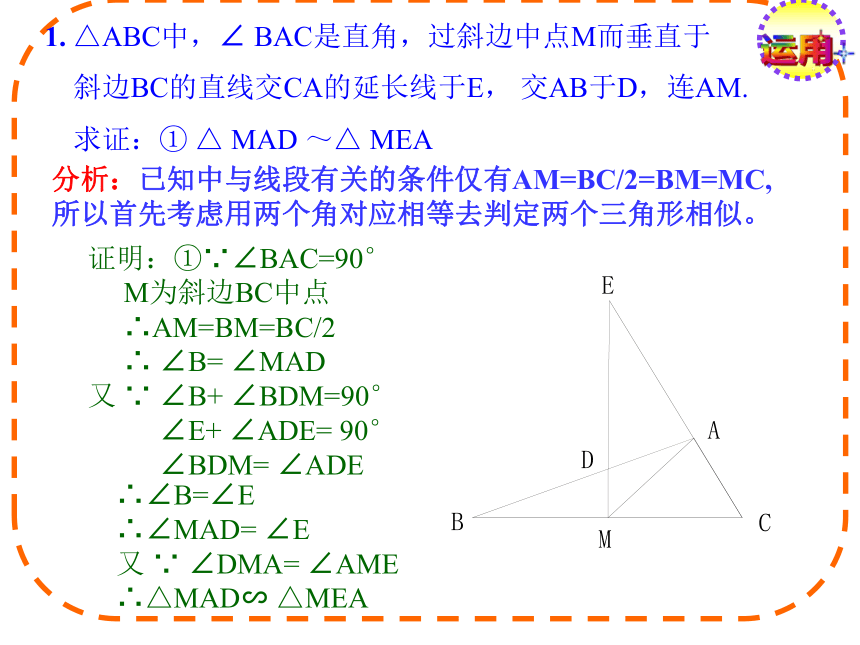
1. △ABC中,∠ BAC是直角,过斜边中点M而垂直于
斜边BC的直线交CA的延长线于E, 交AB于D,连AM.
求证:① △ MAD ~△ MEA
分析:已知中与线段有关的条件仅有AM=BC/2=BM=MC,所以首先考虑用两个角对应相等去判定两个三角形相似。
证明:①∵∠BAC=90°
M为斜边BC中点
∴AM=BM=BC/2
∴ ∠B= ∠MAD
又 ∵ ∠B+ ∠BDM=90°
∠E+ ∠ADE= 90°
∠BDM= ∠ADE
∴∠B=∠E
∴∠MAD= ∠E
又 ∵ ∠DMA= ∠AME
∴△MAD∽ △MEA
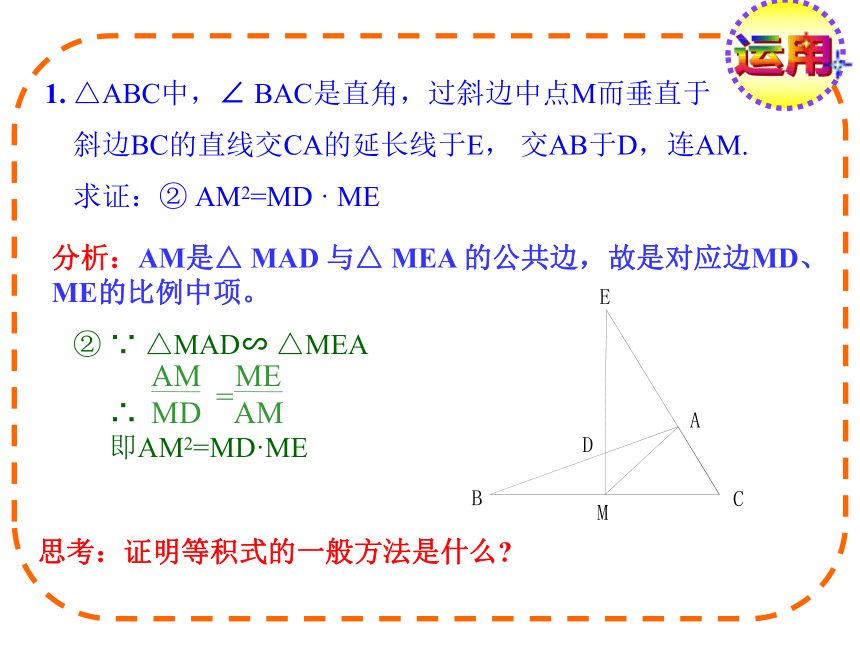
1. △ABC中,∠ BAC是直角,过斜边中点M而垂直于
斜边BC的直线交CA的延长线于E, 交AB于D,连AM.
求证:② AM2=MD · ME
分析:AM是△ MAD 与△ MEA 的公共边,故是对应边MD、ME的比例中项。
② ∵ △MAD∽ △MEA
∴
即AM2=MD·ME
AM
MD
=
ME
AM
思考:证明等积式的一般方法是什么
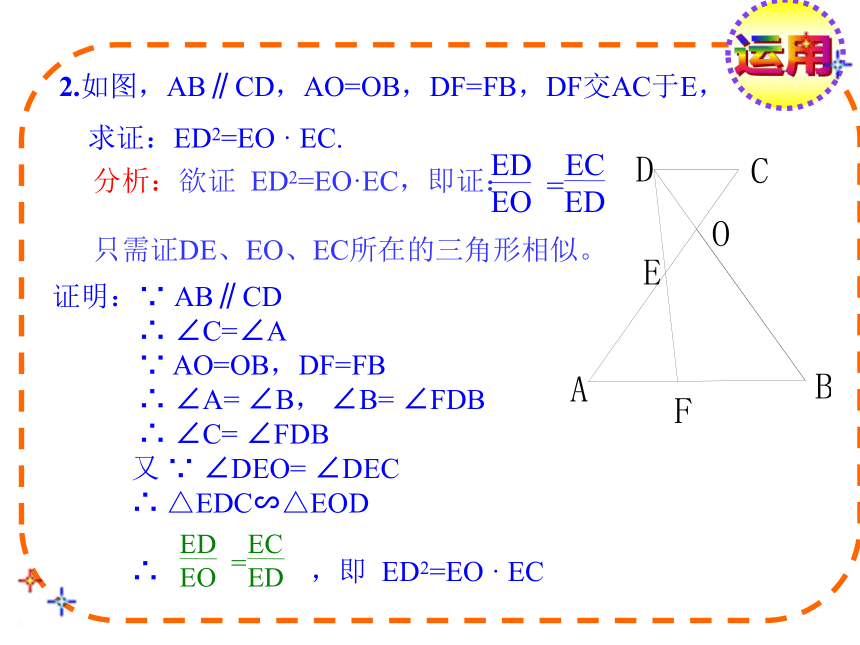
2.如图,AB∥CD,AO=OB,DF=FB,DF交AC于E,
求证:ED2=EO · EC.
分析:欲证 ED2=EO·EC,即证:
只需证DE、EO、EC所在的三角形相似。
ED
EO
=
EC
ED
证明:∵ AB∥CD
∴ ∠C=∠A
∵ AO=OB,DF=FB
∴ ∠A= ∠B, ∠B= ∠FDB
∴ ∠C= ∠FDB
又 ∵ ∠DEO= ∠DEC
∴ △EDC∽△EOD
∴ ,即 ED2=EO · EC
ED
EO
=
EC
ED
3.过◇ABCD的一个顶点A作一直线分别交对角线BD、边BC、边DC的延长线于E、F、G . 求证:EA2 = EF· EG .
分析:要证明
EA2 = EF· EG ,
即 证明 成
立,而EA、EG、EF三条线段在同一直线上,无法构成两个三角形,此时应采用换线段、换比例的方法。可证明:△AED∽△FEB, △AEB ∽ △GED.
证明:∵ AD∥BF AB∥BC
∴△AED ∽△FEB
△AEB ∽△GED
∴
∴
EA
EG
=
AB
DG
EF
EA
=
BE
ED
=
AB
DG
EA
EG
=
EF
EA
4.已知在△ABC中,∠BAC=90°,AD⊥BC,E是AC的
中点,ED交AB的延长线于F. 求证: AB:AC=DF:AF.
分析:因△ABC∽△ABD,所以
要证 即证 ,
需证△BDF∽△DAF.
证明:∵ ∠BAC=90°
AD⊥BC
∴ ∠ABC+∠C= 90°
∠ABC+∠BAD= 90°
∴ ∠BAD= ∠C
∵ ∠ADC= 90°
E是AC的中点,
∴ED=EC
∴ ∠EDC= ∠C
∵ ∠EDC = ∠BDF
∴ ∠BDF= ∠C= ∠BAD
又∵ ∠F =∠F
∴ △BDF∽△DAF.
∴
∵ ∠BAC=90°, AD⊥BC
∴ △ABC∽△ABD
∴
∴
5.D为△ABC的底边BC的延长线上一点,直线DF 交AC于E,且∠FEA=∠AFE .求证:BD·CE=CD·BF
F
E
D
C
B
A
由BD·CE=CD·BF,得
分析:
但△DBF与 △DCE不相似
因此,需作辅助线构造相似三角形
BD
BF
CE
CD
=
5.D为△ABC的底边BC的延长线上一点,直线DF 交AC于E,且∠FEA=∠AFE .求证:BD·CE=CD·BF
F
E
D
C
B
A
G
方法一:
过点C作CG∥AB,交DF于G
则△DCG∽ △DBF
故
再证CG=CE 即可
CD
CG
BF
BD
=
F
E
D
C
B
A
G
方法二:
过点C作CG∥DF,交AB于G
故
再证FG=CE 即可
5.D为△ABC的底边BC的延长线上一点,直线DF 交AC于E,且∠FEA=∠AFE .求证BD·CE=CD·BF
BD
BF
FG
CD
=
F
E
D
C
B
A
G
5.D为△ABC的底边BC的延长线上一点,直线DF 交AC于E,且∠FEA=∠AF.求证:BD·CE=CD·BF
方法三:
过点B作BG∥DF,
交DF的延长线于G
故
再证BG=BF 即可
则△DCE∽ △DBG
DC
CE
BG
DB
=
6.如图: 已知△ABC 中,AD平分∠BAC ,EF是AD的中垂线,EF 交BC的延长线于F .求证:FD2=FC·FB
F
E
D
C
B
A
分析:
由FD2=FC·FB,得
FD
FB
FD
FC
=
但FD、FC、FB都在同一直线上,无法利用相似三角形.
由于FD=FA,替换后可形成相似三角形.
FD
FB
FD
FC
=
FA
FB
FA
FC
=
只要证△FAB∽△FCA即可.
7.已知,AB∥CD∥EF,
(1)图中有几对相似的三角形?
(2)线段AB、CD与EF有怎样的等量关系?
F
A
B
C
D
E
⊿EDC∽⊿EBA
⊿ADC∽⊿AFE
⊿BDA∽⊿EDF
证比例式(或乘积式)的常用方法
证明乘积式时,可先将乘积式改为比例式
(1)找相似三角形(或平行线)
(2)没有相似三角形(或平行线),利用等比例转化,或利用等线段转化,或等积转化,或构造辅助线转化
不经历风雨,怎么见彩虹
没有人能随随便便成功!
一、相似三角形的性质
①相似三角形的对应角相等,对应边成比例.
②相似三角形对应中线的比,对应角平分线的 比,对应高的比,对应周长的比都等于相似比.
③相似三角形面积的比等于相似比的平方.
二.相似三角形的判定方法
定理1 两角对应相等的两个三角形相似.
推论1 平行于三角形一边直线截其它两边(或其延长线),所截得的三角形与原三角形相似;
定理2 三边对应成比例的两个三角形相似.
定理3 两边对应成比例,且夹角相等的两个三角形相似;
定理4 斜边直角边对应成比例的两个直角三角形相似.
1. △ABC中,∠ BAC是直角,过斜边中点M而垂直于
斜边BC的直线交CA的延长线于E, 交AB于D,连AM.
求证:① △ MAD ~△ MEA
分析:已知中与线段有关的条件仅有AM=BC/2=BM=MC,所以首先考虑用两个角对应相等去判定两个三角形相似。
证明:①∵∠BAC=90°
M为斜边BC中点
∴AM=BM=BC/2
∴ ∠B= ∠MAD
又 ∵ ∠B+ ∠BDM=90°
∠E+ ∠ADE= 90°
∠BDM= ∠ADE
∴∠B=∠E
∴∠MAD= ∠E
又 ∵ ∠DMA= ∠AME
∴△MAD∽ △MEA
1. △ABC中,∠ BAC是直角,过斜边中点M而垂直于
斜边BC的直线交CA的延长线于E, 交AB于D,连AM.
求证:② AM2=MD · ME
分析:AM是△ MAD 与△ MEA 的公共边,故是对应边MD、ME的比例中项。
② ∵ △MAD∽ △MEA
∴
即AM2=MD·ME
AM
MD
=
ME
AM
思考:证明等积式的一般方法是什么
2.如图,AB∥CD,AO=OB,DF=FB,DF交AC于E,
求证:ED2=EO · EC.
分析:欲证 ED2=EO·EC,即证:
只需证DE、EO、EC所在的三角形相似。
ED
EO
=
EC
ED
证明:∵ AB∥CD
∴ ∠C=∠A
∵ AO=OB,DF=FB
∴ ∠A= ∠B, ∠B= ∠FDB
∴ ∠C= ∠FDB
又 ∵ ∠DEO= ∠DEC
∴ △EDC∽△EOD
∴ ,即 ED2=EO · EC
ED
EO
=
EC
ED
3.过◇ABCD的一个顶点A作一直线分别交对角线BD、边BC、边DC的延长线于E、F、G . 求证:EA2 = EF· EG .
分析:要证明
EA2 = EF· EG ,
即 证明 成
立,而EA、EG、EF三条线段在同一直线上,无法构成两个三角形,此时应采用换线段、换比例的方法。可证明:△AED∽△FEB, △AEB ∽ △GED.
证明:∵ AD∥BF AB∥BC
∴△AED ∽△FEB
△AEB ∽△GED
∴
∴
EA
EG
=
AB
DG
EF
EA
=
BE
ED
=
AB
DG
EA
EG
=
EF
EA
4.已知在△ABC中,∠BAC=90°,AD⊥BC,E是AC的
中点,ED交AB的延长线于F. 求证: AB:AC=DF:AF.
分析:因△ABC∽△ABD,所以
要证 即证 ,
需证△BDF∽△DAF.
证明:∵ ∠BAC=90°
AD⊥BC
∴ ∠ABC+∠C= 90°
∠ABC+∠BAD= 90°
∴ ∠BAD= ∠C
∵ ∠ADC= 90°
E是AC的中点,
∴ED=EC
∴ ∠EDC= ∠C
∵ ∠EDC = ∠BDF
∴ ∠BDF= ∠C= ∠BAD
又∵ ∠F =∠F
∴ △BDF∽△DAF.
∴
∵ ∠BAC=90°, AD⊥BC
∴ △ABC∽△ABD
∴
∴
5.D为△ABC的底边BC的延长线上一点,直线DF 交AC于E,且∠FEA=∠AFE .求证:BD·CE=CD·BF
F
E
D
C
B
A
由BD·CE=CD·BF,得
分析:
但△DBF与 △DCE不相似
因此,需作辅助线构造相似三角形
BD
BF
CE
CD
=
5.D为△ABC的底边BC的延长线上一点,直线DF 交AC于E,且∠FEA=∠AFE .求证:BD·CE=CD·BF
F
E
D
C
B
A
G
方法一:
过点C作CG∥AB,交DF于G
则△DCG∽ △DBF
故
再证CG=CE 即可
CD
CG
BF
BD
=
F
E
D
C
B
A
G
方法二:
过点C作CG∥DF,交AB于G
故
再证FG=CE 即可
5.D为△ABC的底边BC的延长线上一点,直线DF 交AC于E,且∠FEA=∠AFE .求证BD·CE=CD·BF
BD
BF
FG
CD
=
F
E
D
C
B
A
G
5.D为△ABC的底边BC的延长线上一点,直线DF 交AC于E,且∠FEA=∠AF.求证:BD·CE=CD·BF
方法三:
过点B作BG∥DF,
交DF的延长线于G
故
再证BG=BF 即可
则△DCE∽ △DBG
DC
CE
BG
DB
=
6.如图: 已知△ABC 中,AD平分∠BAC ,EF是AD的中垂线,EF 交BC的延长线于F .求证:FD2=FC·FB
F
E
D
C
B
A
分析:
由FD2=FC·FB,得
FD
FB
FD
FC
=
但FD、FC、FB都在同一直线上,无法利用相似三角形.
由于FD=FA,替换后可形成相似三角形.
FD
FB
FD
FC
=
FA
FB
FA
FC
=
只要证△FAB∽△FCA即可.
7.已知,AB∥CD∥EF,
(1)图中有几对相似的三角形?
(2)线段AB、CD与EF有怎样的等量关系?
F
A
B
C
D
E
⊿EDC∽⊿EBA
⊿ADC∽⊿AFE
⊿BDA∽⊿EDF
证比例式(或乘积式)的常用方法
证明乘积式时,可先将乘积式改为比例式
(1)找相似三角形(或平行线)
(2)没有相似三角形(或平行线),利用等比例转化,或利用等线段转化,或等积转化,或构造辅助线转化
不经历风雨,怎么见彩虹
没有人能随随便便成功!
