高中数学人教A版2019必修第二册 《直线与平面平行---直线与平面平行的判定》名师课件(共26张PPT)
文档属性
| 名称 | 高中数学人教A版2019必修第二册 《直线与平面平行---直线与平面平行的判定》名师课件(共26张PPT) | 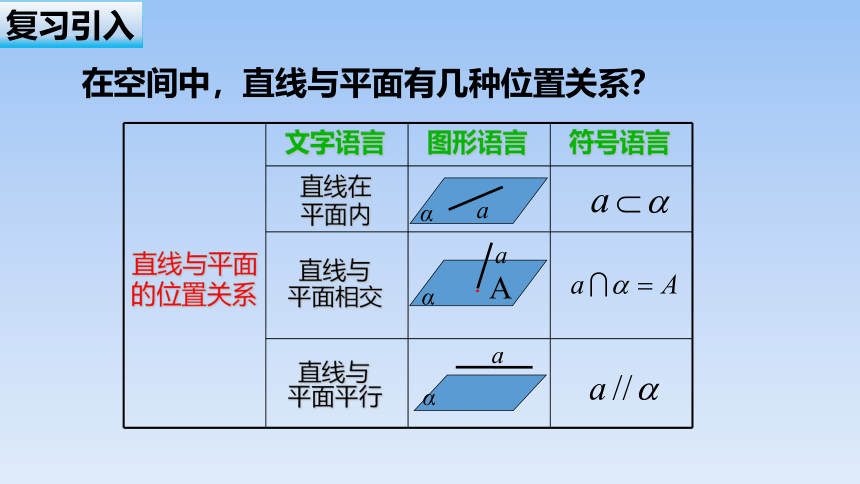 | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-28 10:40:39 | ||
图片预览








文档简介
(共26张PPT)
在空间中,直线与平面有几种位置关系?
文字语言 图形语言 符号语言
直线与平面
的位置关系
α
a
直线在平面内
α
a
直线与
平面平行
直线与
平面相交
复习引入
α
a
.
A
人教A版同步教材名师课件
直线与平面平行
---直线与平面平行的判定
学习目标
学 习 目 标 核心素养
了解平行线的传递性、空间等角定理. 数学抽象
理解直线与平面平行的判定定理、性质定理. 数学抽象
会证明线线平行、线面平行. 逻辑推理
学习目标
课程目标
1.理解直线和平面平行的判定定理并能运用其解决相关问题.
2.通过对判定定理的理解和应用,培养学生的空间转化能力和逻辑推理能力.
数学学科素养
1.逻辑推理:探究归纳直线和平面平行的判定定理,找平行关系;
2.直观想象:题中几何体的点、线、面的位置关系.
在日常生活中,哪些实例给我们以直线与平面平行的印象呢?
探究新知
你的感觉可靠吗?
a
α
怎样判定直线与平面平行呢?
探究新知
问题 1 怎样判断一条直线与平面平行?
定义
直线与平面无公共点
如何判定无公共点?
用定义去判断比较抽象
探究新知
活动:演示开门关门的过程
l
问题 2 门的两边是什么位置关系?
创设情境
问题 3 当门绕轴转动时,门转动的一边与门框所在的平面给人的感觉是什么位置关系?
追问1:不管门如何转动,门转动的一边都与门框所在的平面平行吗?
追问2:需要满足什么条件?
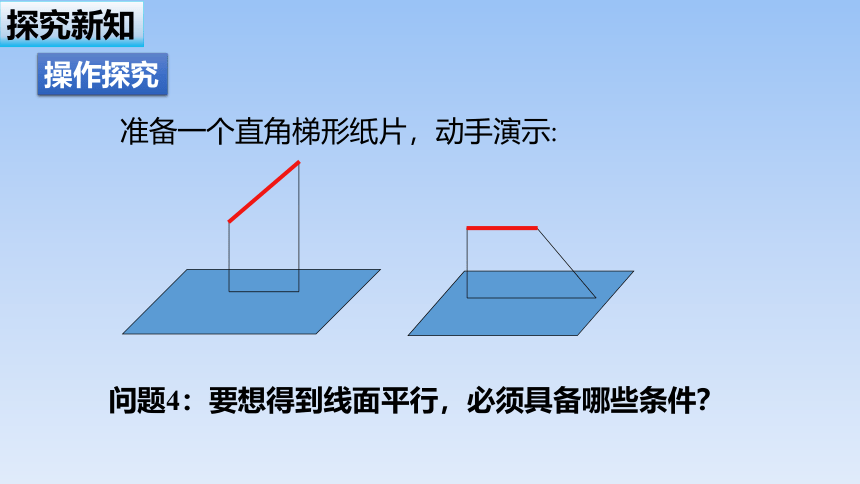
准备一个直角梯形纸片,动手演示:
问题4:要想得到线面平行,必须具备哪些条件?
探究新知
操作探究
共面
不相交
分析:过a、b作平面β,
β
假设a与α相交,设交点为P,
P
则P为α与β的公共点,
即P∈b
从而P 点为a、b的公共点,
这与a//b矛盾.
所以假设不成立,即a//α
为什么?
反证法
探究新知
如图,平面α外的直线a平行于平面α内的直线b
(1)这两条直线共面吗?
(2)直线a与平面α相交吗?
定理 若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
关键词有哪些呢?
线(平面外)线(平面内)平行 线面平行
化归
直线与平面平行(空间)
直线平行(平面)
探究新知
形成定理
判断下列说法是否正确:
①若一条直线不在平面内,则该直线与此平面平行( )
②若一条直线与平面内无数条直线平行,则该直线与此平
面平行( )
③如图,a 是平面α内一条给定的
直线,若平面α外的直线b不平行
于直线a,则直线b与平面α就不
平行( )
b
c
定理辨析
例1、已知P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出结论:
①OM∥PD;②OM∥平面PCD;③OM∥平面PDA;
④OM∥平面PBA;⑤OM∥平面PCB.
其中正确的是________(填序号).
由题意可知OM是△BPD的中位线,所以OM∥PD,①正确;由线面平行的判定定理可知②③都正确.OM与平面PBA及平面PCB都相交,故④⑤不正确.
①②③
典例讲解
解析
例2、如图所示的几何体中,△ABC是任意三角形,AE∥CD,且AE=2a,CD=a,F为BE的中点,求证:DF∥平面ABC.
又CG 平面ABC,DF 平面ABC,
所以DF∥平面ABC.
证明:如图所示,取AB的中点G,连接FG,CG,
典例讲解
因为F、G分别是BE、AB的中点,所以,.
又因为AE=2a,CD=a,所以.
又AE//CD,所以//,
所以四边形为平行四边形,所以//.
(2)证线线平行的方法常用三角形中位线定理、平行四边形性质、平行线分线段成比例定理、平行公理等.
(1)利用直线与平面平行的判定定理证明线面平行,关键是寻找平面内与已知直线平行的直线.
方法归纳
1.(1)如图,四边形ABCD是平行四边形,S是平面ABCD外一点,M为SC的中点,求证:SA∥平面MDB.
(2)如图,在三棱柱ABC A1B1C1中,D,E,F分别是棱AB,BC,A1C1的中点.求证:EF∥平面A1CD.
因为M为SC的中点,O为AC的中点,所以OM∥SA.
因为OM 平面MDB,SA 平面MDB,
所以SA∥平面MDB.
证明:(1)连接AC交BD于点O,连接OM.
变式训练
1.(1)如图,四边形ABCD是平行四边形,S是平面ABCD外一点,M为SC的中点,求证:SA∥平面MDB.
(2)如图,在三棱柱ABC A1B1C1中,D,E,F分别是棱AB,BC,A1C1的中点.求证:EF∥平面A1CD.
变式训练
因为D,E分别是AB,BC的中点,所以DE∥AC且DE=AC.
因为ABC- A1B1C1是三棱柱,所以AA1∥CC1且AA1=CC1,
所以AA1C1C是平行四边形,所以AC∥A1C1且AC=A1C1.
又因为F是A1C1的中点,所以A1F∥AC且A1F= AC,
所以DE∥A1F且DE=A1F,所以四边形A1DEF是平行四边形,所以EF∥A1D,
又EF平面A1CD,A1D 平面A1CD,
所以EF∥平面A1CD.
(2)连接DE.
典例讲解
例3、如图所示,是平行四边形所在平面外一点,是的中点.
求证:∥平面.
解析
如图,连接交于点,易知是的中点,连接.
∵在中,分别为的中点
∴//
又∵ ,
∴//平面
方法归纳
1.应用判定定理证明线面平行的步骤
在平面内找到或作出一条与已知直线平行的直线
找证据
证明已知直线平行于找到(作出)的直线
由判定定理得出结论
上面的第一步“找”是证明的关键,其常用性质定理有:
①基本事实4(平行公理);
②三角形中位线定理;
③平行四边形的性质;
④平行线段成比例.
变式训练
2. 如图所示,已知公共边为的两个全等的矩形和矩形不在同一平面内,分别是对角线上的点,且.
求证://平面
解析
如图,过点P作交BE于点M,过点Q作 交于点,
连接.
又AB=CD,∴PM=QN,四边形PMNQ是平行四边形,
又PQ¢平面CBE,∴PQ //平面CBE.
例4、已知底面是平行四边形的四棱锥P ABCD,点E在PD上,且PE∶ED=2∶1.在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论,若存在,请说出点F的位置.
如图,连接AC、BD交于点O,连接OE,过B点作OE的平行线交PD于点G,过点G作GF∥CE,交PC于点F,连接BF.
因为BG∥OE,BG 平面AEC,OE 平面AEC.所以BG∥平面AEC.
同理GF∥平面AEC.
典例讲解
解析
又BG∩GF=G,所以平面BGF∥平面AEC,
又BF 平面BGF,所以BF与平面AEC无交点,所以BF∥平面AEC.
因为BG∥OE,O是BD的中点,所以E是GD的中点.
又因为PE∶ED=2∶1,所以G是PE的中点.而GF∥CE,所以F为PC的中点.
综上,当点F是PC的中点时,BF∥平面AEC.
方法归纳
立体几何中常见的平行关系是线线平行、线面平行和面面平行,这三种平行关系不是孤立的,而是相互联系、相互转化的,从判定的角度归纳为:
所以平行关系的综合问题的解决必须灵活运用三种平行关系的判定定理.
素养提炼
1.对直线与平面平行的判定定理的理解
(1)线面平行的判定定理具备三个条件:平面外的一条直线、平面内的一条直线、两直线平行,三个条件缺一不可.
(2)定理充分体现了“转化”的思想,它将“线面平行”问题转化为“线线平行”问题,此定理可简化为:线线平行 线面平行.
素养提炼
2.线面平行的判定方法
(1)定义法:证明直线和平面无公共点,一般直接证明较为困难,往往从其反面来证明.
(2)定理法:注意“内、外、平行”三个条件的叙述一定要完备,不可缺失,而应用判定定理的关键是在平面内找到与平面外已知直线平行的直线.常用的方法有:利用三角形的中位线、利用平行四边形的性质、利用平行线的传递性、利用平行线分线段成比例的推论等.
一、直线与平面平行的判定定理
二、运用判定定理时的几个要点
三、立体几何的基本思想:化归
归纳小结
作 业
课本P138练习:2
在空间中,直线与平面有几种位置关系?
文字语言 图形语言 符号语言
直线与平面
的位置关系
α
a
直线在平面内
α
a
直线与
平面平行
直线与
平面相交
复习引入
α
a
.
A
人教A版同步教材名师课件
直线与平面平行
---直线与平面平行的判定
学习目标
学 习 目 标 核心素养
了解平行线的传递性、空间等角定理. 数学抽象
理解直线与平面平行的判定定理、性质定理. 数学抽象
会证明线线平行、线面平行. 逻辑推理
学习目标
课程目标
1.理解直线和平面平行的判定定理并能运用其解决相关问题.
2.通过对判定定理的理解和应用,培养学生的空间转化能力和逻辑推理能力.
数学学科素养
1.逻辑推理:探究归纳直线和平面平行的判定定理,找平行关系;
2.直观想象:题中几何体的点、线、面的位置关系.
在日常生活中,哪些实例给我们以直线与平面平行的印象呢?
探究新知
你的感觉可靠吗?
a
α
怎样判定直线与平面平行呢?
探究新知
问题 1 怎样判断一条直线与平面平行?
定义
直线与平面无公共点
如何判定无公共点?
用定义去判断比较抽象
探究新知
活动:演示开门关门的过程
l
问题 2 门的两边是什么位置关系?
创设情境
问题 3 当门绕轴转动时,门转动的一边与门框所在的平面给人的感觉是什么位置关系?
追问1:不管门如何转动,门转动的一边都与门框所在的平面平行吗?
追问2:需要满足什么条件?
准备一个直角梯形纸片,动手演示:
问题4:要想得到线面平行,必须具备哪些条件?
探究新知
操作探究
共面
不相交
分析:过a、b作平面β,
β
假设a与α相交,设交点为P,
P
则P为α与β的公共点,
即P∈b
从而P 点为a、b的公共点,
这与a//b矛盾.
所以假设不成立,即a//α
为什么?
反证法
探究新知
如图,平面α外的直线a平行于平面α内的直线b
(1)这两条直线共面吗?
(2)直线a与平面α相交吗?
定理 若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
关键词有哪些呢?
线(平面外)线(平面内)平行 线面平行
化归
直线与平面平行(空间)
直线平行(平面)
探究新知
形成定理
判断下列说法是否正确:
①若一条直线不在平面内,则该直线与此平面平行( )
②若一条直线与平面内无数条直线平行,则该直线与此平
面平行( )
③如图,a 是平面α内一条给定的
直线,若平面α外的直线b不平行
于直线a,则直线b与平面α就不
平行( )
b
c
定理辨析
例1、已知P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出结论:
①OM∥PD;②OM∥平面PCD;③OM∥平面PDA;
④OM∥平面PBA;⑤OM∥平面PCB.
其中正确的是________(填序号).
由题意可知OM是△BPD的中位线,所以OM∥PD,①正确;由线面平行的判定定理可知②③都正确.OM与平面PBA及平面PCB都相交,故④⑤不正确.
①②③
典例讲解
解析
例2、如图所示的几何体中,△ABC是任意三角形,AE∥CD,且AE=2a,CD=a,F为BE的中点,求证:DF∥平面ABC.
又CG 平面ABC,DF 平面ABC,
所以DF∥平面ABC.
证明:如图所示,取AB的中点G,连接FG,CG,
典例讲解
因为F、G分别是BE、AB的中点,所以,.
又因为AE=2a,CD=a,所以.
又AE//CD,所以//,
所以四边形为平行四边形,所以//.
(2)证线线平行的方法常用三角形中位线定理、平行四边形性质、平行线分线段成比例定理、平行公理等.
(1)利用直线与平面平行的判定定理证明线面平行,关键是寻找平面内与已知直线平行的直线.
方法归纳
1.(1)如图,四边形ABCD是平行四边形,S是平面ABCD外一点,M为SC的中点,求证:SA∥平面MDB.
(2)如图,在三棱柱ABC A1B1C1中,D,E,F分别是棱AB,BC,A1C1的中点.求证:EF∥平面A1CD.
因为M为SC的中点,O为AC的中点,所以OM∥SA.
因为OM 平面MDB,SA 平面MDB,
所以SA∥平面MDB.
证明:(1)连接AC交BD于点O,连接OM.
变式训练
1.(1)如图,四边形ABCD是平行四边形,S是平面ABCD外一点,M为SC的中点,求证:SA∥平面MDB.
(2)如图,在三棱柱ABC A1B1C1中,D,E,F分别是棱AB,BC,A1C1的中点.求证:EF∥平面A1CD.
变式训练
因为D,E分别是AB,BC的中点,所以DE∥AC且DE=AC.
因为ABC- A1B1C1是三棱柱,所以AA1∥CC1且AA1=CC1,
所以AA1C1C是平行四边形,所以AC∥A1C1且AC=A1C1.
又因为F是A1C1的中点,所以A1F∥AC且A1F= AC,
所以DE∥A1F且DE=A1F,所以四边形A1DEF是平行四边形,所以EF∥A1D,
又EF平面A1CD,A1D 平面A1CD,
所以EF∥平面A1CD.
(2)连接DE.
典例讲解
例3、如图所示,是平行四边形所在平面外一点,是的中点.
求证:∥平面.
解析
如图,连接交于点,易知是的中点,连接.
∵在中,分别为的中点
∴//
又∵ ,
∴//平面
方法归纳
1.应用判定定理证明线面平行的步骤
在平面内找到或作出一条与已知直线平行的直线
找证据
证明已知直线平行于找到(作出)的直线
由判定定理得出结论
上面的第一步“找”是证明的关键,其常用性质定理有:
①基本事实4(平行公理);
②三角形中位线定理;
③平行四边形的性质;
④平行线段成比例.
变式训练
2. 如图所示,已知公共边为的两个全等的矩形和矩形不在同一平面内,分别是对角线上的点,且.
求证://平面
解析
如图,过点P作交BE于点M,过点Q作 交于点,
连接.
又AB=CD,∴PM=QN,四边形PMNQ是平行四边形,
又PQ¢平面CBE,∴PQ //平面CBE.
例4、已知底面是平行四边形的四棱锥P ABCD,点E在PD上,且PE∶ED=2∶1.在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论,若存在,请说出点F的位置.
如图,连接AC、BD交于点O,连接OE,过B点作OE的平行线交PD于点G,过点G作GF∥CE,交PC于点F,连接BF.
因为BG∥OE,BG 平面AEC,OE 平面AEC.所以BG∥平面AEC.
同理GF∥平面AEC.
典例讲解
解析
又BG∩GF=G,所以平面BGF∥平面AEC,
又BF 平面BGF,所以BF与平面AEC无交点,所以BF∥平面AEC.
因为BG∥OE,O是BD的中点,所以E是GD的中点.
又因为PE∶ED=2∶1,所以G是PE的中点.而GF∥CE,所以F为PC的中点.
综上,当点F是PC的中点时,BF∥平面AEC.
方法归纳
立体几何中常见的平行关系是线线平行、线面平行和面面平行,这三种平行关系不是孤立的,而是相互联系、相互转化的,从判定的角度归纳为:
所以平行关系的综合问题的解决必须灵活运用三种平行关系的判定定理.
素养提炼
1.对直线与平面平行的判定定理的理解
(1)线面平行的判定定理具备三个条件:平面外的一条直线、平面内的一条直线、两直线平行,三个条件缺一不可.
(2)定理充分体现了“转化”的思想,它将“线面平行”问题转化为“线线平行”问题,此定理可简化为:线线平行 线面平行.
素养提炼
2.线面平行的判定方法
(1)定义法:证明直线和平面无公共点,一般直接证明较为困难,往往从其反面来证明.
(2)定理法:注意“内、外、平行”三个条件的叙述一定要完备,不可缺失,而应用判定定理的关键是在平面内找到与平面外已知直线平行的直线.常用的方法有:利用三角形的中位线、利用平行四边形的性质、利用平行线的传递性、利用平行线分线段成比例的推论等.
一、直线与平面平行的判定定理
二、运用判定定理时的几个要点
三、立体几何的基本思想:化归
归纳小结
作 业
课本P138练习:2
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
