高中数学人教A版2019必修第二册 《平面与平面平行---平面与平面平行的性质》名师课件(共23张PPT)
文档属性
| 名称 | 高中数学人教A版2019必修第二册 《平面与平面平行---平面与平面平行的性质》名师课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 897.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-28 10:44:00 | ||
图片预览







文档简介
(共23张PPT)
复习:如何判断平面和平面平行
答:有三种方法,一是用定义法,须判断两个平面没有公共点;二是用平面和平面平行的判定定理,须判断一个平面内有两条相交直线都和另一个平面平行.三是平行于同一平面的两平面平行.
思考:如果两个平面平行,会有哪些结论呢
复习引入
人教A版同步教材名师课件
平面与平面平行
---平面与平面平行的性质
学习目标
学 习 目 标 核心素养
掌握平面与平面平行的判定定理,明确由线面平行可推出面面平行. 逻辑推理
掌握平面与平面平行的性质定理,明确由面面平行也可推出线线平行. 逻辑推理
体会线线平行、线面平行、面面平行之间的相互转化关系. 数学抽象
学习目标
课程目标
1.理解平面和平面平行的性质定理并能运用其解决相关问题.
2.通过对性质定理的理解和应用,培养学生的空间转化能力和逻辑推理能力.
数学学科素养
1.逻辑推理:探究归纳平面和平面平行的性质定理,线线平行、线面平行、面面平行之间的转化;
2.直观想象:题中几何体的点、线、面的位置关系.
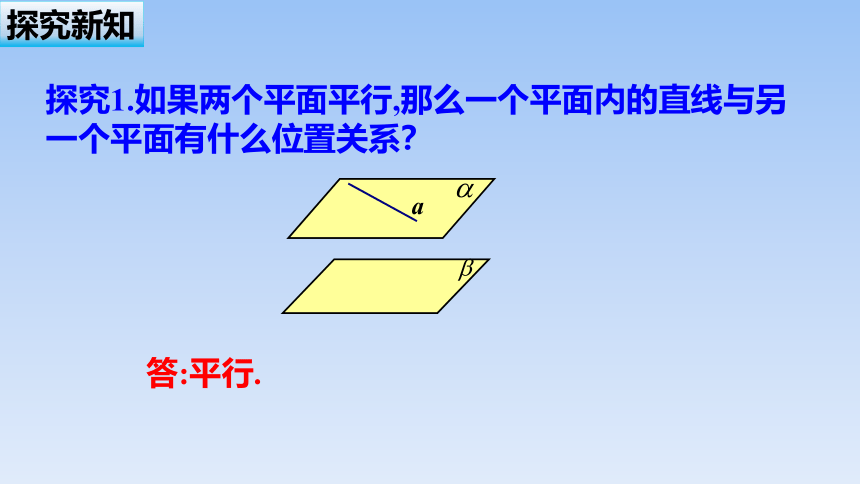
探究1.如果两个平面平行,那么一个平面内的直线与另一个平面有什么位置关系?
a
答:平行.
探究新知
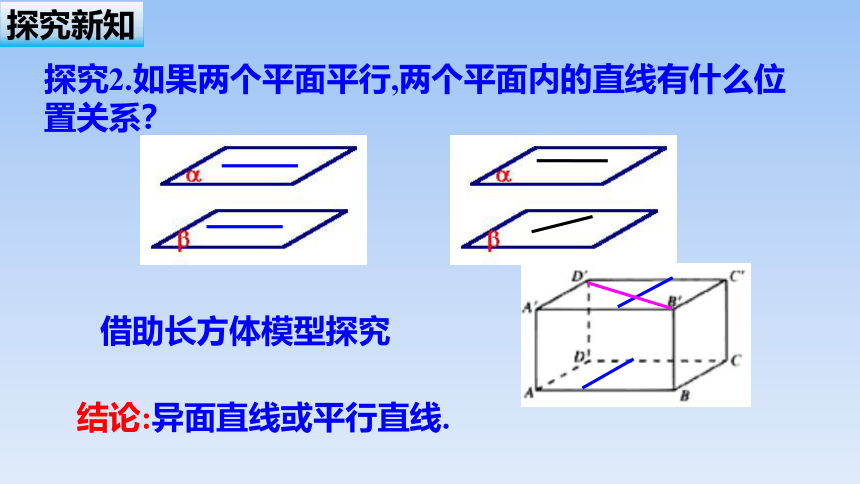
借助长方体模型探究
结论:异面直线或平行直线.
探究2.如果两个平面平行,两个平面内的直线有什么位置关系?
探究新知
探究3:当第三个平面和两个平行平面都相交时,两条交线有什么关系?为什么?
答:两条交线平行.
下面我们来证明这个结论
a
b
α
β
探究新知
如图,平面满足求证:.
证明:∵,∴.
∵,∴没有公共点.
又因为同在平面内,所以.
结论:当第三个平面和两个平行平面都相交时,两条交线平行
探究新知
定理 如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
用符号语言表示性质定理:
想一想:这个定理的作用是什么
答:可以由平面与平面平行得出直线与直线平行
探究新知
例1、 求证:夹在两个平行平面间的平行线段相等.
分析:首先是画出图形,再结合图形将文字语言转化为符号语言,书写出证明过程
如图,
求证:
证明:因为,所以过可作平面且平面与平面和分别相交于和
因为,所以.
因此,四边形是平行四边形. 所以 .
典例讲解
例2、如图,已知α∥β,点P是平面α、β外的一点(不在α与β之间),直线PB、PD分别与α、β相交于点A、B和C、D.
(1)求证:AC∥BD;
(2)已知PA=4 cm,AB=5 cm,PC=3 cm,求PD的长.
典例讲解
(1)证明:因为PB∩PD=P,所以直线PB和PD确定一个平面γ,则α∩γ=AC,β∩γ=BD.又α∥β,所以AC∥BD.
(2)由(1)得AC∥BD,所以= ,所以= ,
所以CD= (cm),所以PD=PC+CD= (cm).
解析
(2)面面平行 线线平行,体现了转化思想与性质定理的交替使用,可实现线线、线面及面面平行的相互转化.
(1)利用面面平行的性质定理证明线线平行的关键是把要证明的直线看作是平面的交线,往往需要有三个平面,即有两平面平行,再构造第三个面与两平行平面都相交.
方法归纳
1.(1)如图所示,P是三角形ABC所在平面外一点,平面α∥平面ABC,α分别交线段PA,PB,PC于A′,B′,C′.若PA′∶AA′=2∶5,则△A′B′C′与△ABC的面积比为( )
A.2∶5 B.2∶7 C.4∶49 D.9∶25
(2)如图,在三棱柱ABC A1B1C1中,M是A1C1的中点,平面AB1M∥平面BC1N,AC∩平面BC1N=N.
求证:N为AC的中点.
变式训练
C
证明:因为平面AB1M∥平面BC1N,平面ACC1A1∩平面AB1M=AM,平面BC1N∩平面ACC1A1=C1N,所以C1N∥AM.
又AC∥A1C1,所以四边形ANC1M为平行四边形,所以AN∥C1M且AN=C1M,
又C1M=A1C1,A1C1=AC,所以AN=AC,所以N为AC的中点.
例3、已知正三棱柱ABC A′B′C′中,D是AA′上的点,E是B′C′的中点,且A′E∥平面DBC′.试判断D点在AA′上的位置,并给出证明.
D点为AA′的中点.
证明如下:
取BC的中点F,连接AF,EF,
设EF与BC′交于点O,连接OD,易证A′E∥AF,A′E=AF.
易知A′,E,F,A共面于平面A′EFA,因为A′E∥平面DBC′,
A′E 平面A′EFA,
且平面DBC′∩平面A′EFA=DO,所以A′E∥DO.
在平行四边形A′EFA中,
因为O是EF的中点(因为EC′∥BF,且EC′=BF),
所以D点为AA′的中点.
典例讲解
解析
解答平行问题探索性题目的注意事项
(1)有中点这一条件时,一般试探性的以中点为基础作辅助线或面,然后再证明是否满足条件.
(2)关于平行的性质定理是作证算的理论依据.
(3)一般步骤:取点、连线、成形→探索论证→计算(作答).
方法归纳
2.如图所示,已知P是 平行四边形 ABCD所在平面外一点,M、N分别是AB、PC的中点,平面PAD∩平面PBC=l.
(1)求证:l∥BC;
(2)MN与平面PAD是否平行?试证明你的结论.
(2)平行.
证明如下:取PD的中点E,连接AE,NE,可以证得NE∥AM且NE=AM.可知四边形AMNE为平行四边形.所以MN∥AE,又因为MN 平面APD,AE 平面APD,所以MN∥平面APD.
解:法一:(1)证明:因为BC∥AD,BC 平面PAD,AD 平面PAD,所以BC∥平面PAD.
又因为平面PBC∩平面PAD=l,所以BC∥l.
变式训练
法二:(1)证明:由于AD∥BC,AD 平面PBC,BC 平面PBC,所以AD∥平面PBC.
又因为平面PBC∩平面PAD=l,所以 l ∥AD ,l∥BC.
(2)平行.证明如下:设Q是CD的中点,连接NQ,MQ,则MQ∥AD,NQ∥PD,而MQ∩NQ=Q,AD∩PD=D,所以平面MNQ∥平面PAD.又MN 平面MNQ,所以MN∥平面PAD.
1.面面平行的性质定理给出了证明线线平行的一种方法,同时该定理还可推出:“两个平面平行,其中一个平面内的直线必平行于另一个平面”,即“面面平行 线面平行”.
2.三种平行关系的转化
三种平行关系是紧密相连的,可以任意转化,其相互转化关系如图所示:
素养提炼
3.证明线线、线面、面面平行的一般思路
“见了已知想性质,见了求证想判定”,也就是说“发现已知,转化结论,沟通已知与未知的关系”.这是分析问题和解决问题的一般思维方法,而作辅助线和辅助面往往是沟通已知和未知的有效手段.
素养提炼
当堂练习
1.已知平面 ,则下列命题正确的是( )
A. 内所有直线平行
B. 内的无数条直线平行
C. 内的任何一条直线都不平行
D. 内的一条直线平行
2.在正方体中,相互平行的面不会是( )
A.前后相对侧面 B.上下相对底面 C.左右相对侧面 D.相邻的侧面
B
D
当堂练习
4.过正方体 ABDC-A1B1C1D1的三顶点A1,C1,B的平面与底面ABCD所在平面的交线为,则与A1C1的位置关系是___________.
平行
3.如图,在正方体中,下列四对截面彼此平行的一对是( )
A.平面E1FG1与平面EGH1
B.平面FHG1与平面F1H1G
C.平面F1H1H与平面FHE1
D.平面E1HG1与平面EH1G
A
1、两个平面平行具有如下的一些性质:
(1)如果两个平面平行,那么在一个平面内的所有直线都与另一个平面平行.
(2)如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
(3)如果一条直线和两个平行平面中的一个相交,那么它也和另一个平面相交.
(4)夹在两个平行平面间的所有平行线段相等.
归纳小结
2、线线平行、线面平行、面面平行,要注意这里平行关系的互相转化.
3、在应用相关定理时要注意辅助线、辅助面的作法.
归纳小结
G
H
作 业
复习:如何判断平面和平面平行
答:有三种方法,一是用定义法,须判断两个平面没有公共点;二是用平面和平面平行的判定定理,须判断一个平面内有两条相交直线都和另一个平面平行.三是平行于同一平面的两平面平行.
思考:如果两个平面平行,会有哪些结论呢
复习引入
人教A版同步教材名师课件
平面与平面平行
---平面与平面平行的性质
学习目标
学 习 目 标 核心素养
掌握平面与平面平行的判定定理,明确由线面平行可推出面面平行. 逻辑推理
掌握平面与平面平行的性质定理,明确由面面平行也可推出线线平行. 逻辑推理
体会线线平行、线面平行、面面平行之间的相互转化关系. 数学抽象
学习目标
课程目标
1.理解平面和平面平行的性质定理并能运用其解决相关问题.
2.通过对性质定理的理解和应用,培养学生的空间转化能力和逻辑推理能力.
数学学科素养
1.逻辑推理:探究归纳平面和平面平行的性质定理,线线平行、线面平行、面面平行之间的转化;
2.直观想象:题中几何体的点、线、面的位置关系.
探究1.如果两个平面平行,那么一个平面内的直线与另一个平面有什么位置关系?
a
答:平行.
探究新知
借助长方体模型探究
结论:异面直线或平行直线.
探究2.如果两个平面平行,两个平面内的直线有什么位置关系?
探究新知
探究3:当第三个平面和两个平行平面都相交时,两条交线有什么关系?为什么?
答:两条交线平行.
下面我们来证明这个结论
a
b
α
β
探究新知
如图,平面满足求证:.
证明:∵,∴.
∵,∴没有公共点.
又因为同在平面内,所以.
结论:当第三个平面和两个平行平面都相交时,两条交线平行
探究新知
定理 如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
用符号语言表示性质定理:
想一想:这个定理的作用是什么
答:可以由平面与平面平行得出直线与直线平行
探究新知
例1、 求证:夹在两个平行平面间的平行线段相等.
分析:首先是画出图形,再结合图形将文字语言转化为符号语言,书写出证明过程
如图,
求证:
证明:因为,所以过可作平面且平面与平面和分别相交于和
因为,所以.
因此,四边形是平行四边形. 所以 .
典例讲解
例2、如图,已知α∥β,点P是平面α、β外的一点(不在α与β之间),直线PB、PD分别与α、β相交于点A、B和C、D.
(1)求证:AC∥BD;
(2)已知PA=4 cm,AB=5 cm,PC=3 cm,求PD的长.
典例讲解
(1)证明:因为PB∩PD=P,所以直线PB和PD确定一个平面γ,则α∩γ=AC,β∩γ=BD.又α∥β,所以AC∥BD.
(2)由(1)得AC∥BD,所以= ,所以= ,
所以CD= (cm),所以PD=PC+CD= (cm).
解析
(2)面面平行 线线平行,体现了转化思想与性质定理的交替使用,可实现线线、线面及面面平行的相互转化.
(1)利用面面平行的性质定理证明线线平行的关键是把要证明的直线看作是平面的交线,往往需要有三个平面,即有两平面平行,再构造第三个面与两平行平面都相交.
方法归纳
1.(1)如图所示,P是三角形ABC所在平面外一点,平面α∥平面ABC,α分别交线段PA,PB,PC于A′,B′,C′.若PA′∶AA′=2∶5,则△A′B′C′与△ABC的面积比为( )
A.2∶5 B.2∶7 C.4∶49 D.9∶25
(2)如图,在三棱柱ABC A1B1C1中,M是A1C1的中点,平面AB1M∥平面BC1N,AC∩平面BC1N=N.
求证:N为AC的中点.
变式训练
C
证明:因为平面AB1M∥平面BC1N,平面ACC1A1∩平面AB1M=AM,平面BC1N∩平面ACC1A1=C1N,所以C1N∥AM.
又AC∥A1C1,所以四边形ANC1M为平行四边形,所以AN∥C1M且AN=C1M,
又C1M=A1C1,A1C1=AC,所以AN=AC,所以N为AC的中点.
例3、已知正三棱柱ABC A′B′C′中,D是AA′上的点,E是B′C′的中点,且A′E∥平面DBC′.试判断D点在AA′上的位置,并给出证明.
D点为AA′的中点.
证明如下:
取BC的中点F,连接AF,EF,
设EF与BC′交于点O,连接OD,易证A′E∥AF,A′E=AF.
易知A′,E,F,A共面于平面A′EFA,因为A′E∥平面DBC′,
A′E 平面A′EFA,
且平面DBC′∩平面A′EFA=DO,所以A′E∥DO.
在平行四边形A′EFA中,
因为O是EF的中点(因为EC′∥BF,且EC′=BF),
所以D点为AA′的中点.
典例讲解
解析
解答平行问题探索性题目的注意事项
(1)有中点这一条件时,一般试探性的以中点为基础作辅助线或面,然后再证明是否满足条件.
(2)关于平行的性质定理是作证算的理论依据.
(3)一般步骤:取点、连线、成形→探索论证→计算(作答).
方法归纳
2.如图所示,已知P是 平行四边形 ABCD所在平面外一点,M、N分别是AB、PC的中点,平面PAD∩平面PBC=l.
(1)求证:l∥BC;
(2)MN与平面PAD是否平行?试证明你的结论.
(2)平行.
证明如下:取PD的中点E,连接AE,NE,可以证得NE∥AM且NE=AM.可知四边形AMNE为平行四边形.所以MN∥AE,又因为MN 平面APD,AE 平面APD,所以MN∥平面APD.
解:法一:(1)证明:因为BC∥AD,BC 平面PAD,AD 平面PAD,所以BC∥平面PAD.
又因为平面PBC∩平面PAD=l,所以BC∥l.
变式训练
法二:(1)证明:由于AD∥BC,AD 平面PBC,BC 平面PBC,所以AD∥平面PBC.
又因为平面PBC∩平面PAD=l,所以 l ∥AD ,l∥BC.
(2)平行.证明如下:设Q是CD的中点,连接NQ,MQ,则MQ∥AD,NQ∥PD,而MQ∩NQ=Q,AD∩PD=D,所以平面MNQ∥平面PAD.又MN 平面MNQ,所以MN∥平面PAD.
1.面面平行的性质定理给出了证明线线平行的一种方法,同时该定理还可推出:“两个平面平行,其中一个平面内的直线必平行于另一个平面”,即“面面平行 线面平行”.
2.三种平行关系的转化
三种平行关系是紧密相连的,可以任意转化,其相互转化关系如图所示:
素养提炼
3.证明线线、线面、面面平行的一般思路
“见了已知想性质,见了求证想判定”,也就是说“发现已知,转化结论,沟通已知与未知的关系”.这是分析问题和解决问题的一般思维方法,而作辅助线和辅助面往往是沟通已知和未知的有效手段.
素养提炼
当堂练习
1.已知平面 ,则下列命题正确的是( )
A. 内所有直线平行
B. 内的无数条直线平行
C. 内的任何一条直线都不平行
D. 内的一条直线平行
2.在正方体中,相互平行的面不会是( )
A.前后相对侧面 B.上下相对底面 C.左右相对侧面 D.相邻的侧面
B
D
当堂练习
4.过正方体 ABDC-A1B1C1D1的三顶点A1,C1,B的平面与底面ABCD所在平面的交线为,则与A1C1的位置关系是___________.
平行
3.如图,在正方体中,下列四对截面彼此平行的一对是( )
A.平面E1FG1与平面EGH1
B.平面FHG1与平面F1H1G
C.平面F1H1H与平面FHE1
D.平面E1HG1与平面EH1G
A
1、两个平面平行具有如下的一些性质:
(1)如果两个平面平行,那么在一个平面内的所有直线都与另一个平面平行.
(2)如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
(3)如果一条直线和两个平行平面中的一个相交,那么它也和另一个平面相交.
(4)夹在两个平行平面间的所有平行线段相等.
归纳小结
2、线线平行、线面平行、面面平行,要注意这里平行关系的互相转化.
3、在应用相关定理时要注意辅助线、辅助面的作法.
归纳小结
G
H
作 业
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
