高中数学人教A版2019必修第二册8.5.2直线与直线平行_导学案(含答案)
文档属性
| 名称 | 高中数学人教A版2019必修第二册8.5.2直线与直线平行_导学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 279.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-28 12:11:15 | ||
图片预览


文档简介
8.5.1 直线与直线平行
1.正确理解基本事实4和等角定理;
2.能用基本事实4和等角定理解决一些简单的相关问题.
1.直观想象:基本事实4及等角定理的理解;
2.逻辑推理:基本事实4及等角定理的应用.
重点:能用基本事实4和等角定理解决一些简单的相关问题.
难点:能用基本事实4和等角定理解决一些简单的相关问题.
预习导入
阅读课本133-135页,填写。
1.平行线的传递性
基本事实4:平行于同一条直线的两条直线___________.
符号表示:a∥b,b∥c a∥c.
2.定理
空间中如果两个角的两边分别对应平行,那么这两个角_____________.
1.已知∠BAC=30°,AB∥A′B′,AC∥A′C′,则∠B′A′C′等于( )
(A)30° (B)150°
(C)30°或150° (D)大小无法确定
2.下列四个结论中假命题的个数是( )
①垂直于同一直线的两条直线互相平行;
②平行于同一直线的两直线平行;
③若直线a,b,c满足a∥b,b⊥c,则a⊥c;
④若直线l1,l2是异面直线,则与l1,l2都相交的两条直线是异面直线.
(A)1 (B)2 (C)3 (D)4
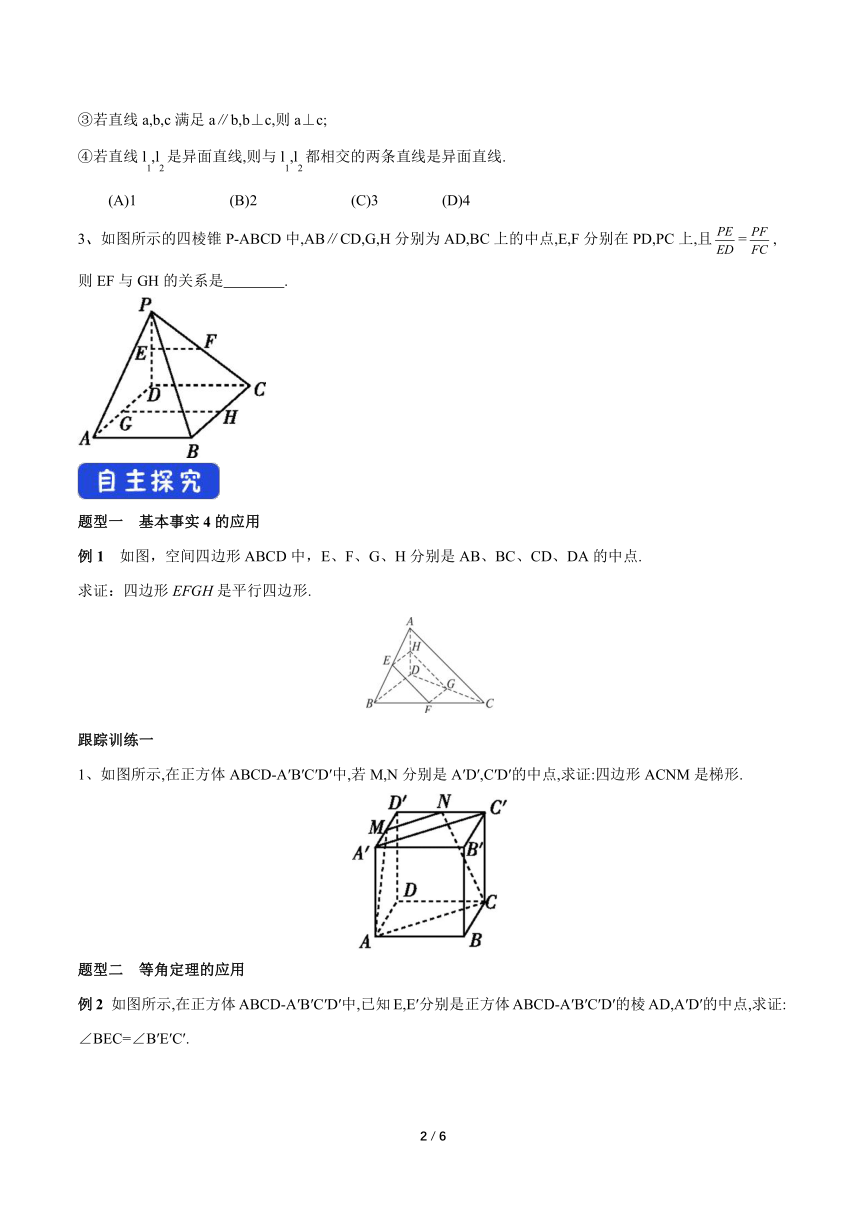
3、如图所示的四棱锥P-ABCD中,AB∥CD,G,H分别为AD,BC上的中点,E,F分别在PD,PC上,且=,则EF与GH的关系是 .
题型一 基本事实4的应用
例1 如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
跟踪训练一
1、如图所示,在正方体ABCD-A′B′C′D′中,若M,N分别是A′D′,C′D′的中点,求证:四边形ACNM是梯形.
题型二 等角定理的应用
例2 如图所示,在正方体ABCD-A′B′C′D′中,已知E,E′分别是正方体ABCD-A′B′C′D′的棱AD,A′D′的中点,求证:∠BEC=∠B′E′C′.
跟踪训练二
1、在正方体ABCD-A1B1C1D1中,E,F分别为AD,AB的中点,M,N分别为B1C1,C1D1的中点.
求证:(1)MC∥A1E,A1F∥CN; (2)∠EA1F=∠NCM.
1.空间四边形的两条对角线相互垂直,顺次连接四边中点的四边形一定是( )
(A)空间四边形
(B)矩形
(C)菱形
(D)正方形
2.在三棱锥P ABC中,PC与AB所成的角为70°,E,F,G分别为PA,PB,AC的中点,则∠FEG等于( )
(A)20° (B)70°
(C)110° (D)70°或110°
3.平面内直线上有两个不同点到直线的距离相等,则两直线的位置关系是______.
4.已知,,,则等于______.
5.如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点且AC=BD.
求证:四边形EFGH是菱形.
答案
小试牛刀
1. C
2.B
3.平行
自主探究
例1 【答案】证明见解析.
【解析】证明:连接EH,因为EH是△ABD的中位线,
所以EH∥BD,且EH=.
同理,FG∥BD,且FG=.
所以EH∥FG,且EH=FG.
所以四边形EFGH为平行四边形.
跟踪训练一
1、【答案】证明见解析.
【解析】如图所示,连接A′C′,
因为M,N分别是A′D′,C′D′的中点,
所以MN∥A′C′,且MN=A′C′.
由正方体的性质可知
A′C′∥AC,且A′C′=AC.
所以MN∥AC,且MN=AC, 所以四边形ACNM是梯形.
例2 【答案】证明见解析.
【解析】证明:如图所示,连接EE′.
因为E,E′分别是AD,A′D′的中点,
所以AE∥A′E′,且AE=A′E′.
所以四边形AEE′A′是平行四边形.
所以AA′∥EE′,且AA′=EE′.
又因为AA′∥BB′,且AA′=BB′,所以EE′∥BB′,且EE′=BB′.
所以四边形BEE′B′是平行四边形.
所以BE∥B′E′.
同理可证CE∥C′E′.
又∠BEC与∠B′E′C′的两边方向相同,
所以∠BEC=∠B′E′C′.
跟踪训练二
1、【答案】D.
【解析】证明 (1)取A1D1的中点I,连接DI,MI,
因为M为B1C1的中点,ABCD-A1B1C1D1为正方体,
所以C1D1CD,MIC1D1,
根据基本事实4知CDMI,
故IDCM为平行四边形,
所以MC∥ID,
又I,E分别为A1D1,AD的中点,
所以A1IED,
所以A1IDE为平行四边形,
所以A1E∥ID.
故MC∥A1E.
同理可证A1F∥CN.
(2)由(1)知A1F∥CN,MC∥A1E,
又A1E,A1F与CM,CN的方向分别相反,
所以∠EA1F=∠NCM.
当堂检测
1-2. BD
3. 平行或相交或重合
4. 或
5.【答案】证明见解析
【解析】证明:连接EH,因为EH是△ABD的中位线,所以EH∥BD,且EH=.
同理,FG∥BD,EF∥AC,且FG=,EF=.
所以EH∥FG,且EH=FG.所以四边形EFGH为平行四边形.
因为AC=BD,所以EF=EH.
所以四边形EFGH为菱形.
2 / 2
1.正确理解基本事实4和等角定理;
2.能用基本事实4和等角定理解决一些简单的相关问题.
1.直观想象:基本事实4及等角定理的理解;
2.逻辑推理:基本事实4及等角定理的应用.
重点:能用基本事实4和等角定理解决一些简单的相关问题.
难点:能用基本事实4和等角定理解决一些简单的相关问题.
预习导入
阅读课本133-135页,填写。
1.平行线的传递性
基本事实4:平行于同一条直线的两条直线___________.
符号表示:a∥b,b∥c a∥c.
2.定理
空间中如果两个角的两边分别对应平行,那么这两个角_____________.
1.已知∠BAC=30°,AB∥A′B′,AC∥A′C′,则∠B′A′C′等于( )
(A)30° (B)150°
(C)30°或150° (D)大小无法确定
2.下列四个结论中假命题的个数是( )
①垂直于同一直线的两条直线互相平行;
②平行于同一直线的两直线平行;
③若直线a,b,c满足a∥b,b⊥c,则a⊥c;
④若直线l1,l2是异面直线,则与l1,l2都相交的两条直线是异面直线.
(A)1 (B)2 (C)3 (D)4
3、如图所示的四棱锥P-ABCD中,AB∥CD,G,H分别为AD,BC上的中点,E,F分别在PD,PC上,且=,则EF与GH的关系是 .
题型一 基本事实4的应用
例1 如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
跟踪训练一
1、如图所示,在正方体ABCD-A′B′C′D′中,若M,N分别是A′D′,C′D′的中点,求证:四边形ACNM是梯形.
题型二 等角定理的应用
例2 如图所示,在正方体ABCD-A′B′C′D′中,已知E,E′分别是正方体ABCD-A′B′C′D′的棱AD,A′D′的中点,求证:∠BEC=∠B′E′C′.
跟踪训练二
1、在正方体ABCD-A1B1C1D1中,E,F分别为AD,AB的中点,M,N分别为B1C1,C1D1的中点.
求证:(1)MC∥A1E,A1F∥CN; (2)∠EA1F=∠NCM.
1.空间四边形的两条对角线相互垂直,顺次连接四边中点的四边形一定是( )
(A)空间四边形
(B)矩形
(C)菱形
(D)正方形
2.在三棱锥P ABC中,PC与AB所成的角为70°,E,F,G分别为PA,PB,AC的中点,则∠FEG等于( )
(A)20° (B)70°
(C)110° (D)70°或110°
3.平面内直线上有两个不同点到直线的距离相等,则两直线的位置关系是______.
4.已知,,,则等于______.
5.如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点且AC=BD.
求证:四边形EFGH是菱形.
答案
小试牛刀
1. C
2.B
3.平行
自主探究
例1 【答案】证明见解析.
【解析】证明:连接EH,因为EH是△ABD的中位线,
所以EH∥BD,且EH=.
同理,FG∥BD,且FG=.
所以EH∥FG,且EH=FG.
所以四边形EFGH为平行四边形.
跟踪训练一
1、【答案】证明见解析.
【解析】如图所示,连接A′C′,
因为M,N分别是A′D′,C′D′的中点,
所以MN∥A′C′,且MN=A′C′.
由正方体的性质可知
A′C′∥AC,且A′C′=AC.
所以MN∥AC,且MN=AC, 所以四边形ACNM是梯形.
例2 【答案】证明见解析.
【解析】证明:如图所示,连接EE′.
因为E,E′分别是AD,A′D′的中点,
所以AE∥A′E′,且AE=A′E′.
所以四边形AEE′A′是平行四边形.
所以AA′∥EE′,且AA′=EE′.
又因为AA′∥BB′,且AA′=BB′,所以EE′∥BB′,且EE′=BB′.
所以四边形BEE′B′是平行四边形.
所以BE∥B′E′.
同理可证CE∥C′E′.
又∠BEC与∠B′E′C′的两边方向相同,
所以∠BEC=∠B′E′C′.
跟踪训练二
1、【答案】D.
【解析】证明 (1)取A1D1的中点I,连接DI,MI,
因为M为B1C1的中点,ABCD-A1B1C1D1为正方体,
所以C1D1CD,MIC1D1,
根据基本事实4知CDMI,
故IDCM为平行四边形,
所以MC∥ID,
又I,E分别为A1D1,AD的中点,
所以A1IED,
所以A1IDE为平行四边形,
所以A1E∥ID.
故MC∥A1E.
同理可证A1F∥CN.
(2)由(1)知A1F∥CN,MC∥A1E,
又A1E,A1F与CM,CN的方向分别相反,
所以∠EA1F=∠NCM.
当堂检测
1-2. BD
3. 平行或相交或重合
4. 或
5.【答案】证明见解析
【解析】证明:连接EH,因为EH是△ABD的中位线,所以EH∥BD,且EH=.
同理,FG∥BD,EF∥AC,且FG=,EF=.
所以EH∥FG,且EH=FG.所以四边形EFGH为平行四边形.
因为AC=BD,所以EF=EH.
所以四边形EFGH为菱形.
2 / 2
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
