4.4.3不同增长函数的差异 课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共32张PPT)
文档属性
| 名称 | 4.4.3不同增长函数的差异 课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 21.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-28 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
人教2019A版必修 第一册
4.4.3 不同增长函数的差异
第四章 指数函数与对数函数
1.了解指数函数、对数函数、线性函数 (一次函数) 的增长差异.
2.理解对数增长、直线上升、指数爆炸。
3.了解函数的建模过程。
学习目标
我们看到,一次函数与指数函数的增长方式存在很大差异.事实上,这种差异正是不同类型现实问题具有不同增长规律的反映.因此,如果把握了不同函数增长方式的差异,那么就可以根据现实问题的增长情况,选择合适的函数模型刻画其变化规律.下面就来研究一次函数、指数函数和对数函数增长方式的差异.
问题导入
我们仍然采用由特殊到一般,由具体到抽象的研究方法.
下面就来研究一次函数 f(x)=kx+b,k>0 ,指数函数g(x)=ax(a>1) ,
对数函数 在定义域内增长方式的差异.
问题探究
方法
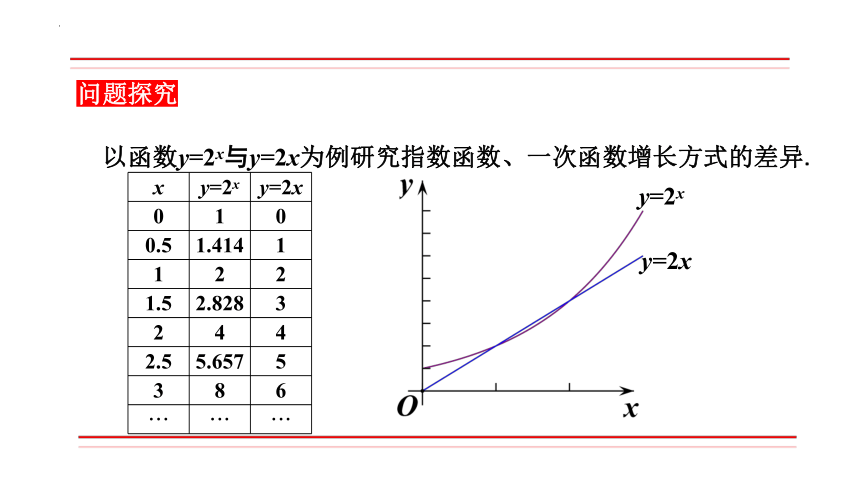
以函数y=2x与y=2x为例研究指数函数、一次函数增长方式的差异.
分析:
(1) 在区间(-∞,0)上,指数函数y=2x值恒大于0,一次函数y=2x值恒小于0,
所以我们重点研究在区间(0,+∞)上它们的增长差异.
(2) 借助信息技术,在同一直角坐标系内列表、描点作图如下:
问题探究
以函数y=2x与y=2x为例研究指数函数、一次函数增长方式的差异.
问题探究
x y=2x y=2x
0 1 0
0.5 1.414 1
1 2 2
1.5 2.828 3
2 4 4
2.5 5.657 5
3 8 6
··· ··· ···
y=2x
y=2x
以函数y=2x与y=2x为例研究指数函数、一次函数增长方式的差异.
问题探究
(3) 观察两个函数图象及其增长方式:
结论1:函数y=2x与y=2x有两个交点(1,2)和(2,4)
结论2:在区间(0,1)上,函数y=2x的图象位于y=2x之上
结论3:在区间(1,2)上,函数y=2x的图象位于y=2x之下
结论4:在区间(2,3)上,函数y=2x的图象位于y=2x之上
以函数y=2x与y=2x为例研究指数函数、一次函数增长方式的差异.
问题探究
综上:虽然函数y=2x与y=2x都是增函数,但是它们的增长速度不同,函数y=2x的增长速度不变,但是y=2x的增长速度改变,先慢后快.
问题探究
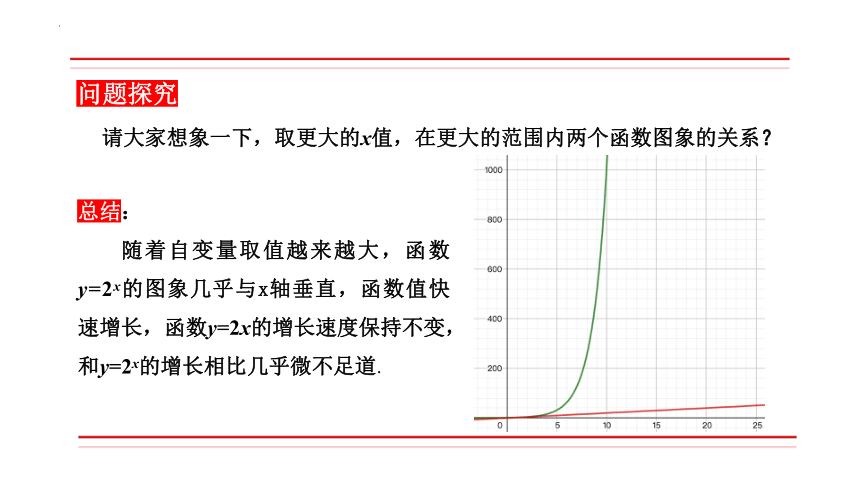
总结:
随着自变量取值越来越大,函数y=2x的图象几乎与x轴垂直,函数值快速增长,函数y=2x的增长速度保持不变,和y=2x的增长相比几乎微不足道.
请大家想象一下,取更大的x值,在更大的范围内两个函数图象的关系?
函数y=2x与y=2x在[0,+∞)上增长快慢的不同如下:
虽然函数y=2x与y=2x在[0,+∞)上都是单调递增,但它们的增长速度不同.
随着x的增大,y=2x的增长速度越来越快,会超过并远远大于y=2x的增长速度.
尽管在x的一定范围内,2x<2x,但由于y=2x的增长最终会快于y=2x的增长,
因此,总会存在一个x0,当x>x0时,恒有2x>2x.
归纳总结
一般地指数函数y=ax(a>1)与一次函数y=kx(k>0)的增长差异都与上述情况类似.
即使k值远远大于a值,指数函数y=ax(a>1)虽然有一段区间会小于y=kx(k>0),但总会存在一个x0,当x>x0时, y=ax(a>1)的增长速度会大大超过y=kx(k>0)的增长速度.
归纳总结
概括:
练习
2.已知三个变量y1,y2,y3随着变量x的变化情况如下表:
则关于x分别呈对数型函数、指数型函数、幂函数型函数变化的变量依次为( )
A.y1,y2,y3 B.y2,y1,y3 C.y3,y2,y1 D.y1,y3,y2
解析:通过指数型函数、对数型函数、幂函数型函数的增长规律比较可知,对数型函数的增长速度越来越慢,变量y3随x的变化符合此规律;指数型函数的增长是爆炸式增长,y2随x的变化符合此规律;幂函数型函数的增长速度越来越快,y1随x的变化符合此规律,故选C.
分析:
(1) 在区间(-∞,0)上,对数函数y=lgx没意义,一次函数值恒小于0,
所以研究在区间(0,+∞)上它们的增长差异.
(2) 借助信息技术,在同一直角坐标系内列表、描点作图如下:
以函数y=lgx与 为例研究对数函数、一次函数增长方式的差异.
问题探究
以函数y=lgx与 为例研究对数函数、一次函数增长方式的差异.
问题探究
x y=lgx
0 不存在 0
10 1 1
20 1.301 2
30 1.477 3
40 1.602 4
50 1.699 5
60 1.778 6
··· ··· ···
y=lgx
以函数y=lgx与 为例研究对数函数、一次函数增长方式的差异.
问题探究
(3) 观察两个函数图象及其增长方式:
总结一:虽然函数y=lgx与 在(0,+∞)上都是单调递增,但它们的增长速度存在明显差异.
在(0,+∞)上增长速度不变,y=lgx在(0,+∞)上的增长速度在变化.
随着x的增大, 的图象离x轴越来越远,而函数y=lgx的图象越来越平缓,就像与x轴平行一样.
以函数y=lgx与 为例研究对数函数、一次函数增长方式的差异.
问题探究
例如:lg10=1,lg100=2,lg1000=3,lg10000=4;
这表明,当x>10,即y>1,y=lgx比 相比增长得就很慢了.
y=lgx
思考:将y=lgx放大1000倍,将函数y=1000lgx与 比较,仍有上面规律吗?先想象一下,仍然有.
一般地,虽然对数函数 与一次函数y=kx(k>0)在(0,+∞)上都是单调递增,但它们的增长速度不同.
随着x的增大,一次函数y=kx(k>0)保持固定的增长速度,而对数函数
的增长速度越来越慢.
不论a值比k值大多少,在一定范围内, 可能会大于kx,但由于
的增长最值会慢于kx的增长,因此总存在一个x0,当x>x0时,恒有 . 。
归纳总结
3.函数f(x)=2x和g(x)=x3的图象如图所示.设两函数的图象交于点A(x1,y1),B(x2,y2),且x1(1)指出图中曲线C1,C2分别对应的函数;
(2)结合函数图象,判断f(6),g(6),f(2 019),g(2 019)的大小.
解:(1)C1对应的函数为g(x)=x3,C2对应的函数为f(x)=2x.
(2)因为f(1)>g(1),f(2)g(10),
所以1所以x1<6x2,
从图象上可以看出,
当x1当x>x2时,f(x)>g(x),所以f(2 019)>g(2 019).
因为g(2 019)>g(6),所以f(2 019)>g(2 019)>g(6)>f(6).
6.某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资的函数模型为y=k1x,B产品的利润与投资的函数模型为y=k2xα(利润和投资的单位为百万元),其关系分别如图①,图②所示.
(1)分别求出A,B两种产品的利润与投资的函数关系式;
(2)该企业已筹集到资金1千万元,并准备全部投入到A,B两种产品的生产中,问怎样分配这1千万元,才能使企业获得最大利润,其最大利润为多少 (精确到万元)
故投资A产品844万元,投资B产品156万元时,总利润最大,最大值约为578万元.
解题方法(由图象判断指数函数、对数函数和幂函数的方法)
根据图象判断增长型的指数函数、对数函数和幂函数时,
通常是观察函数图象上升得快慢,
即随着自变量的增长,图象最“陡”的函数是指数函数,
图象趋于平缓的函数是对数函数.
人教2019A版必修 第一册
4.4.3 不同增长函数的差异
第四章 指数函数与对数函数
1.了解指数函数、对数函数、线性函数 (一次函数) 的增长差异.
2.理解对数增长、直线上升、指数爆炸。
3.了解函数的建模过程。
学习目标
我们看到,一次函数与指数函数的增长方式存在很大差异.事实上,这种差异正是不同类型现实问题具有不同增长规律的反映.因此,如果把握了不同函数增长方式的差异,那么就可以根据现实问题的增长情况,选择合适的函数模型刻画其变化规律.下面就来研究一次函数、指数函数和对数函数增长方式的差异.
问题导入
我们仍然采用由特殊到一般,由具体到抽象的研究方法.
下面就来研究一次函数 f(x)=kx+b,k>0 ,指数函数g(x)=ax(a>1) ,
对数函数 在定义域内增长方式的差异.
问题探究
方法
以函数y=2x与y=2x为例研究指数函数、一次函数增长方式的差异.
分析:
(1) 在区间(-∞,0)上,指数函数y=2x值恒大于0,一次函数y=2x值恒小于0,
所以我们重点研究在区间(0,+∞)上它们的增长差异.
(2) 借助信息技术,在同一直角坐标系内列表、描点作图如下:
问题探究
以函数y=2x与y=2x为例研究指数函数、一次函数增长方式的差异.
问题探究
x y=2x y=2x
0 1 0
0.5 1.414 1
1 2 2
1.5 2.828 3
2 4 4
2.5 5.657 5
3 8 6
··· ··· ···
y=2x
y=2x
以函数y=2x与y=2x为例研究指数函数、一次函数增长方式的差异.
问题探究
(3) 观察两个函数图象及其增长方式:
结论1:函数y=2x与y=2x有两个交点(1,2)和(2,4)
结论2:在区间(0,1)上,函数y=2x的图象位于y=2x之上
结论3:在区间(1,2)上,函数y=2x的图象位于y=2x之下
结论4:在区间(2,3)上,函数y=2x的图象位于y=2x之上
以函数y=2x与y=2x为例研究指数函数、一次函数增长方式的差异.
问题探究
综上:虽然函数y=2x与y=2x都是增函数,但是它们的增长速度不同,函数y=2x的增长速度不变,但是y=2x的增长速度改变,先慢后快.
问题探究
总结:
随着自变量取值越来越大,函数y=2x的图象几乎与x轴垂直,函数值快速增长,函数y=2x的增长速度保持不变,和y=2x的增长相比几乎微不足道.
请大家想象一下,取更大的x值,在更大的范围内两个函数图象的关系?
函数y=2x与y=2x在[0,+∞)上增长快慢的不同如下:
虽然函数y=2x与y=2x在[0,+∞)上都是单调递增,但它们的增长速度不同.
随着x的增大,y=2x的增长速度越来越快,会超过并远远大于y=2x的增长速度.
尽管在x的一定范围内,2x<2x,但由于y=2x的增长最终会快于y=2x的增长,
因此,总会存在一个x0,当x>x0时,恒有2x>2x.
归纳总结
一般地指数函数y=ax(a>1)与一次函数y=kx(k>0)的增长差异都与上述情况类似.
即使k值远远大于a值,指数函数y=ax(a>1)虽然有一段区间会小于y=kx(k>0),但总会存在一个x0,当x>x0时, y=ax(a>1)的增长速度会大大超过y=kx(k>0)的增长速度.
归纳总结
概括:
练习
2.已知三个变量y1,y2,y3随着变量x的变化情况如下表:
则关于x分别呈对数型函数、指数型函数、幂函数型函数变化的变量依次为( )
A.y1,y2,y3 B.y2,y1,y3 C.y3,y2,y1 D.y1,y3,y2
解析:通过指数型函数、对数型函数、幂函数型函数的增长规律比较可知,对数型函数的增长速度越来越慢,变量y3随x的变化符合此规律;指数型函数的增长是爆炸式增长,y2随x的变化符合此规律;幂函数型函数的增长速度越来越快,y1随x的变化符合此规律,故选C.
分析:
(1) 在区间(-∞,0)上,对数函数y=lgx没意义,一次函数值恒小于0,
所以研究在区间(0,+∞)上它们的增长差异.
(2) 借助信息技术,在同一直角坐标系内列表、描点作图如下:
以函数y=lgx与 为例研究对数函数、一次函数增长方式的差异.
问题探究
以函数y=lgx与 为例研究对数函数、一次函数增长方式的差异.
问题探究
x y=lgx
0 不存在 0
10 1 1
20 1.301 2
30 1.477 3
40 1.602 4
50 1.699 5
60 1.778 6
··· ··· ···
y=lgx
以函数y=lgx与 为例研究对数函数、一次函数增长方式的差异.
问题探究
(3) 观察两个函数图象及其增长方式:
总结一:虽然函数y=lgx与 在(0,+∞)上都是单调递增,但它们的增长速度存在明显差异.
在(0,+∞)上增长速度不变,y=lgx在(0,+∞)上的增长速度在变化.
随着x的增大, 的图象离x轴越来越远,而函数y=lgx的图象越来越平缓,就像与x轴平行一样.
以函数y=lgx与 为例研究对数函数、一次函数增长方式的差异.
问题探究
例如:lg10=1,lg100=2,lg1000=3,lg10000=4;
这表明,当x>10,即y>1,y=lgx比 相比增长得就很慢了.
y=lgx
思考:将y=lgx放大1000倍,将函数y=1000lgx与 比较,仍有上面规律吗?先想象一下,仍然有.
一般地,虽然对数函数 与一次函数y=kx(k>0)在(0,+∞)上都是单调递增,但它们的增长速度不同.
随着x的增大,一次函数y=kx(k>0)保持固定的增长速度,而对数函数
的增长速度越来越慢.
不论a值比k值大多少,在一定范围内, 可能会大于kx,但由于
的增长最值会慢于kx的增长,因此总存在一个x0,当x>x0时,恒有 . 。
归纳总结
3.函数f(x)=2x和g(x)=x3的图象如图所示.设两函数的图象交于点A(x1,y1),B(x2,y2),且x1
(2)结合函数图象,判断f(6),g(6),f(2 019),g(2 019)的大小.
解:(1)C1对应的函数为g(x)=x3,C2对应的函数为f(x)=2x.
(2)因为f(1)>g(1),f(2)
所以1
从图象上可以看出,
当x1
因为g(2 019)>g(6),所以f(2 019)>g(2 019)>g(6)>f(6).
6.某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资的函数模型为y=k1x,B产品的利润与投资的函数模型为y=k2xα(利润和投资的单位为百万元),其关系分别如图①,图②所示.
(1)分别求出A,B两种产品的利润与投资的函数关系式;
(2)该企业已筹集到资金1千万元,并准备全部投入到A,B两种产品的生产中,问怎样分配这1千万元,才能使企业获得最大利润,其最大利润为多少 (精确到万元)
故投资A产品844万元,投资B产品156万元时,总利润最大,最大值约为578万元.
解题方法(由图象判断指数函数、对数函数和幂函数的方法)
根据图象判断增长型的指数函数、对数函数和幂函数时,
通常是观察函数图象上升得快慢,
即随着自变量的增长,图象最“陡”的函数是指数函数,
图象趋于平缓的函数是对数函数.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
