4.3.1等比数列的概念(第2课时) 课件-2022-2023学年高二上学期数学人教A版(2019)选择性必修第二册(共19张PPT)
文档属性
| 名称 | 4.3.1等比数列的概念(第2课时) 课件-2022-2023学年高二上学期数学人教A版(2019)选择性必修第二册(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 947.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-28 00:00:00 | ||
图片预览





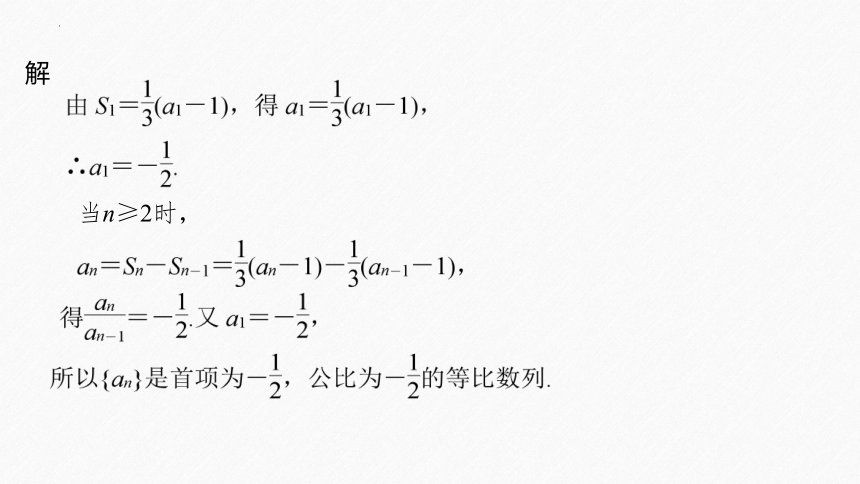

文档简介
(共19张PPT)
等比数列的概念
第2课时
学习目标
1.掌握等比数列的判断及证明方法.
2.能根据等比数列的定义推出等比数列的性质,并能运用这些性质简化运算.
1.等比数列的定义
复习回顾
2.等比数列的通项公式
思想方法:累乘法 迭代法
an=a1qn-1
新课探究一
判定与证明方法
1.定义法:
2.等比中项法:
3.通项公式法:
如何判定与证明一个数列是等比数列
an=A·qn(A≠0).
例1
例题讲解
已知数列{an}的前n项和为Sn,Sn= (n∈N*).
求证:数列{an}是等比数列.
解
当n≥2时,
已知数列{an}的前n项和为Sn,且对任意的n∈N*有an+Sn=n.
设bn=an-1,求证:数列{bn}是等比数列;
解:由a1+S1=1及a1=S1,得a1=2
由 an+Sn=n
得 an+1+Sn+1=n+1,
相减得 an+1-an+an+1=1,
∴2an+1=an+1. ∴2(an+1-1)=an-1,即2bn+1=bn.∴数列{bn}是以b1=a1-1=-2为首项,2为公比的等比数列.
试一试
判断一个数列是等比数列的常用方法
(2)通项公式法:若数列{an}的通项公式为an=a1qn-1(a1≠0,q≠0),则数列{an}是等比数列.
(3)等比中项法:若 =anan+2(n∈N*且an≠0),则数列{an}为等比数列.
小结
类比等差数列通项公式的性质,你能得到等比数列中相似的性质吗?
an=amqn-m.
新知探究二
(1)由等比数列的定义可知
=qn-m
(2)若m+n=k+l,m,n,k,l∈N*.
aman=akal.
例2.
例题讲解
①已知a5=8,a7=2,an>0,求an.
②若an>0,a5a7+2a6a8+a6a10=49,求a6+a8;
解:(1)
由等比中项,化简条件得
即(a6+a8)2=49,
∵an>0,
∴a6+a8=7.
(2)
有四个实数,前三个数成等比数列,且它们的乘积为216,后三个数成等差数列,且它们的和为12,求这四个数.
试一试
所以a3=216.
所以a=6.
由题意知第4个数为12q-6.
所以6+6q+12q-6=12,
故所求的四个数为9,6,4,2.
方法二 设后三个数为4-d,4,4+d,
解得4-d=6.
所以d=-2.
故所求得的四个数为9,6,4,2.
1.已知数列{an}是等比数列,a3+a7=20,a1a9=64,求a11的值.
课堂练习
解1∵{an}为等比数列,
∴a1·a9=a3·a7=64.
又∵a3+a7=20,
∴a3=4,a7=16或a3=16,a7=4.
此时a11=a3q8=4×42=64.
∵a7·a14=a4·a17=6,a4+a17=5,
∴a4与a17为方程x2-5x+6=0的两个根,
解得a4=2,a17=3或a4=3,a17=2,
∵an>an+1,∴a4=3,a17=2,
解2
课堂小结
1. 等比数列的证明
2.等比数列通项公式的性质及其应用
等比数列的概念
第2课时
学习目标
1.掌握等比数列的判断及证明方法.
2.能根据等比数列的定义推出等比数列的性质,并能运用这些性质简化运算.
1.等比数列的定义
复习回顾
2.等比数列的通项公式
思想方法:累乘法 迭代法
an=a1qn-1
新课探究一
判定与证明方法
1.定义法:
2.等比中项法:
3.通项公式法:
如何判定与证明一个数列是等比数列
an=A·qn(A≠0).
例1
例题讲解
已知数列{an}的前n项和为Sn,Sn= (n∈N*).
求证:数列{an}是等比数列.
解
当n≥2时,
已知数列{an}的前n项和为Sn,且对任意的n∈N*有an+Sn=n.
设bn=an-1,求证:数列{bn}是等比数列;
解:由a1+S1=1及a1=S1,得a1=2
由 an+Sn=n
得 an+1+Sn+1=n+1,
相减得 an+1-an+an+1=1,
∴2an+1=an+1. ∴2(an+1-1)=an-1,即2bn+1=bn.∴数列{bn}是以b1=a1-1=-2为首项,2为公比的等比数列.
试一试
判断一个数列是等比数列的常用方法
(2)通项公式法:若数列{an}的通项公式为an=a1qn-1(a1≠0,q≠0),则数列{an}是等比数列.
(3)等比中项法:若 =anan+2(n∈N*且an≠0),则数列{an}为等比数列.
小结
类比等差数列通项公式的性质,你能得到等比数列中相似的性质吗?
an=amqn-m.
新知探究二
(1)由等比数列的定义可知
=qn-m
(2)若m+n=k+l,m,n,k,l∈N*.
aman=akal.
例2.
例题讲解
①已知a5=8,a7=2,an>0,求an.
②若an>0,a5a7+2a6a8+a6a10=49,求a6+a8;
解:(1)
由等比中项,化简条件得
即(a6+a8)2=49,
∵an>0,
∴a6+a8=7.
(2)
有四个实数,前三个数成等比数列,且它们的乘积为216,后三个数成等差数列,且它们的和为12,求这四个数.
试一试
所以a3=216.
所以a=6.
由题意知第4个数为12q-6.
所以6+6q+12q-6=12,
故所求的四个数为9,6,4,2.
方法二 设后三个数为4-d,4,4+d,
解得4-d=6.
所以d=-2.
故所求得的四个数为9,6,4,2.
1.已知数列{an}是等比数列,a3+a7=20,a1a9=64,求a11的值.
课堂练习
解1∵{an}为等比数列,
∴a1·a9=a3·a7=64.
又∵a3+a7=20,
∴a3=4,a7=16或a3=16,a7=4.
此时a11=a3q8=4×42=64.
∵a7·a14=a4·a17=6,a4+a17=5,
∴a4与a17为方程x2-5x+6=0的两个根,
解得a4=2,a17=3或a4=3,a17=2,
∵an>an+1,∴a4=3,a17=2,
解2
课堂小结
1. 等比数列的证明
2.等比数列通项公式的性质及其应用
