5.1 任意角和弧度制 课时练习-2022-2023学年高一上学期数学人教A版(2019)必修第一册(含答案)
文档属性
| 名称 | 5.1 任意角和弧度制 课时练习-2022-2023学年高一上学期数学人教A版(2019)必修第一册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-28 16:07:28 | ||
图片预览




文档简介
5.1任意角和弧度制课时练习
一、单选题
1.与角终边相同的角可以表示为( )
A. B.
C. D.
2.早在两千年前,古人就通过观测发现地面是球面,并会运用巧妙的方法对地球半径进行估算.如图所示,把太阳光视为平行光线,O为地球球心,A,B为北半球上同一经度的两点,且A,B之间的经线长度为L,于同一时刻在A,B两点分别竖立一根长杆和,通过测量得到两根长杆与太阳光的夹角和(和的单位为弧度),由此可计算地球的半径为( )
A. B. C. D.
3.圆心在原点,半径为10的圆上的两个动点M,N同时从点出发,沿圆周运动,点M按逆时针方向旋转,速度为弧度/秒,点N按顺时针方向旋转,速度为弧度/秒,则它们第三次相遇时点M转过的弧度数为( )
A. B. C. D.
4.若是锐角,则,是( )
A.第一象限角 B.第三象限角
C.第一象限角或第三象限角 D.第二象限角或第四象限角
5.“角a与β的终边关于直线对称”是“”的( )
A.充分必要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
6.一个扇形的弧长与面积的数值都是3,则该扇形圆心角的弧度数为( )
A. B. C. D.2
7.已知扇形的面积为8,且圆心角弧度数为2,则扇形的周长为( )
A.32 B.24 C. D.
8.如今我们在测量视力的时候,常用对数视力表(如图),视力值从4.0到5.3,每行相差0.1,这种计算视力的方法称为五分记录法,“对数视力表”和“五分记录法”是由我国著名眼科专家缪天荣(1914—2005)在1959年研制发明的,这种独创的视力表的核心在于:将视力和视角设定为对数关系,因此被认为是一种最符合视力生理的,而又便于统计和计算的视力检测系统,这使中国的眼科研究一下子站到了世界的巅峰,1986年,《对数视力表》在第25届国际眼科大会(罗马)宣读,引起轰动,1990年《标准对数视力表》被制定为国家标准(GB11533—89),并在全国实施.已知在五分记录法中,规定视力值,其中为人眼的视角,单位为分(1度=60分),视角的大小,决定了人眼能看到的最小物体的长度,这个长度约等于以眼球为圆心(眼球大小忽略不计),视角为圆心角,眼球与物体之间的距离为半径的扇形的弧长.如果某人的一只眼睛的视力值为4.7,那么这只眼睛能看到距离5米外的最小物体的长度约为(参考数据:,)( )
A.1.5毫米 B.2.9毫米 C.4.4毫米 D.5.8毫米
9.已知扇形的周长是6cm,面积是,则扇形的中心角的弧度数是( )
A.1 B.4 C.1或4 D.2或4
10.如图所示的时钟显示的时刻为4:30,设半个小时后时针与分针的夹角为,则( )
A. B. C. D.
11.已知集合,则下列选项正确的是( )
A. B. C. D.
12.折扇是我国传统文化的延续,在我国已有四千年左右的历史,“扇”与“善”谐音,折扇也寓意“善良”“善行”.它常以字画的形式体现我国的传统文化,也是运筹帷幄、决胜千里、大智大勇的象征(如图1),图2为其结构简化图,设扇面A,B间的圆弧长为l,AB间的弦长为d,圆弧所对的圆心角为(为弧度角),则l、d和所满足的恒等关系为( ).
A. B.
C. D.
13.已知点,则角的终边在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
14.若={α|,B={第一或第四象限角},则A、B关系为( )
A.A=B B.AB C.AB D.非A、B、C结论
15.如图是一个近似扇形的湖面,其中,弧的长为.为了方便观光,欲在两点之间修建一条笔直的走廊.若当时,,扇形的面积记为,则的值约为( )
A. B.
C. D.
二、填空题
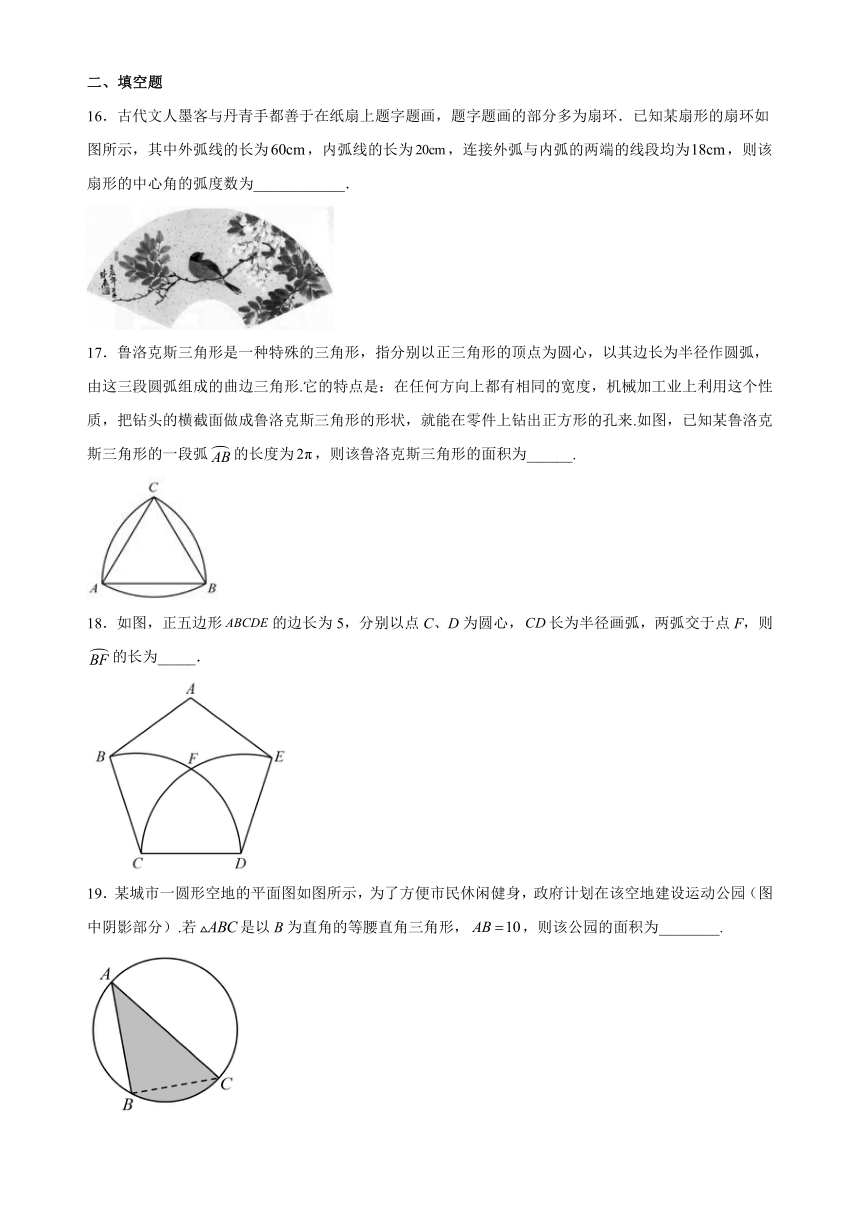
16.古代文人墨客与丹青手都善于在纸扇上题字题画,题字题画的部分多为扇环.已知某扇形的扇环如图所示,其中外弧线的长为,内弧线的长为,连接外弧与内弧的两端的线段均为,则该扇形的中心角的弧度数为____________.
17.鲁洛克斯三角形是一种特殊的三角形,指分别以正三角形的顶点为圆心,以其边长为半径作圆弧,由这三段圆弧组成的曲边三角形.它的特点是:在任何方向上都有相同的宽度,机械加工业上利用这个性质,把钻头的横截面做成鲁洛克斯三角形的形状,就能在零件上钻出正方形的孔来.如图,已知某鲁洛克斯三角形的一段弧的长度为,则该鲁洛克斯三角形的面积为______.
18.如图,正五边形的边长为5,分别以点C、D为圆心,长为半径画弧,两弧交于点F,则的长为_____.
19.某城市一圆形空地的平面图如图所示,为了方便市民休闲健身,政府计划在该空地建设运动公园(图中阴影部分).若是以B为直角的等腰直角三角形,,则该公园的面积为________.
20.已知圆锥的底面半径为2,其侧面展开扇形的圆心角大小为,则这个圆锥的母线长为______.
三、解答题
21.(1)写出与终边相同的角的集合S,并把S中适合不等式的元素α写出来:
(2)已知扇形AOB的周长为8,面积为3,求圆心角的大小;
22.有一个圆锥形漏斗,其底面直径是10cm,母线长为20cm,在漏斗口的点处用一根绳子将漏斗挂在墙面上,当绳子的长度最短时,可以紧紧地箍住漏斗,不会上下滑动,求此时绳子的长度.
23.如图,一图形由一个扇形与两个正三角形组成,其中扇形的周长为,圆心角的弧度数为,半径为.
(1)若,求;
(2)设该图形的面积为,写出关于的函数表达式.
参考答案:
1.A
【分析】先求出相近的终边相同的角,即可判断.
【详解】与角终边相同的角为,故与角终边相同的角可以表示为.
故选:A
2.A
【分析】过点B作太阳光的平行线,与 的延长线交于点C,可求出,利用弧长公式即可求得地球的半径.
【详解】如图所示,过点B作太阳光的平行线,与 的延长线交于点C,
则 , ,所以,
设地球半径为R,则根据弧长公式得 ,所以 ,
故选:A.
3.C
【分析】根据两点相遇一次转过弧度之和为即可求解.
【详解】由题意,动点第三次相遇,则两个动点转过的弧度之和为:,
设从点出发秒后点第三次相遇,则,解得秒,
此时点转过的弧度数为弧度
故选:C
4.C
【分析】根据取奇数和偶数分类讨论即可求解.
【详解】是锐角,,,当k为奇数时,为第三象限角;当k为偶数时,为第一象限角.所以为第一象限角或第三象限角.
故选:C.
5.C
【分析】根据终边关于对称,得两角的关系,再由,得两角满足的关系,根据充分必要条件的定义即可求解.
【详解】角与的终边关于直线对称,则,
.
反之,当时,则,从而角a与β的终边不一定关于直线对称.
故“角与的终边关于直线对称”是“”的充分不必要条件.
故选:C
6.C
【分析】由扇形的弧长公式和面积公式列方程组求解.
【详解】设扇形的圆心角的弧度数为α,半径为r,则解得
故选:C.
7.D
【分析】根据扇形面积和弧长公式即可求解.
【详解】圆心角,扇形面积,
即,得半径,
所以弧长,
故扇形的周长.
故选:D
8.B
【分析】由视力值求出视角,再由计算出弧长即得.
【详解】由题意得,解得分,则圆心角为2分,半径为5米的扇形的弧长等于米=2.9毫米.
故选:B.
9.C
【分析】根据给定条件,利用扇形面积公式求出扇形所在圆半径,再借助弧长公式求解作答.
【详解】设扇形所在圆半径为r,则扇形弧长为,依题意,,解得或,
所以扇形的中心角的弧度数是或.
故选:C
10.B
【分析】由题意,根据时钟的特性,结合弧度制的写法,可得答案.
【详解】半小时后是5:00整,时针指向5,分针指向12,.
故选:B.
11.B
【分析】可确定在上集合和集合的关系,然后结合角的周期性得结论.
【详解】在范围,集合含有,集合含有,
由角的周期性变化可知:,
故选:B.
12.A
【分析】利用弧长公式及直角三角形中的正弦公式,化简即可得到答案.
【详解】解:设扇形的半径为R,如图,由弧长公式,得,在直角三角形中,
化简得.
故选:A.
13.B
【分析】根据象限角概念求解即可.
【详解】因为,所以的终边在第二象限.
故选:B
14.D
【分析】在集合与中举例说明即可判断.
【详解】集合中,若,不属于第一或第四象限角,即.
集合中,若,是第一象限角,但.
综上,集合与没有关系.
故选:D
15.B
【分析】由题可得,再根据扇形面积公式可得,结合条件即得.
【详解】设扇形的圆心角为,则,
在中,,
又,
∴,又,
∴.
故选:B.
16.
【分析】根据扇形弧长与扇形的中心角的弧度数为的关系,可求得,进而可得该扇形的中心角的弧度数.
【详解】解:如图,
依题意可得弧的长为,弧的长为,设扇形的中心角的弧度数为
则,则,即.
因为,所以,所以该扇形的中心角的弧度数.
故答案为:.
17.
【分析】由弧长公式可求得等边的边长,再根据该鲁洛克斯三角形的面积等于三个扇形的面积减去2个的面积,结合扇形和三角形的面积公式即可得解.
【详解】解:由题意可知,
设,
则弧的长度为,所以,
设弧所对的扇形的面积为,
,
则该鲁洛克斯三角形的面积为.
故答案为:.
18.
【分析】本题关键在于如何得到所对圆心角,利用圆半径得到为等边三角形得出,再利用正多变形内角,从而得出,然后代入公式即可得出答案.
【详解】连接,,由题可得,
则是等边三角形,
,
在正五边形中,,
,
的长,
故答案为:.
19.
【分析】利用扇形面积公式即可得到结果.
【详解】由题可知圆心为的中点,,连接,
该公园的面积
故答案为:
20.12
【分析】设母线长为,由弧长公式计算可得;
【详解】解:设母线长为,则侧面展开的扇形的弧长为,
由题意,即,因为,故.
故答案为:
21.(1),;(2)6或.
【分析】(1)由终边相同的角的表示直接得,对取值得符合条件得角;
(2)由扇形面积公式与弧长公式求解即可
【详解】(1)与角终边相同的角的集合为,
当时,时,时,;
中适合不等式的元素为:;
(2)设扇形的半径为,中心角为,则.
由题意可得:,
又.
联立解得或.
22.cm
【分析】由圆锥的展开图可知,绳子是线段时,绳子长度最短,根据扇形弧长公式可求圆心角,从而可求弦的长度.
【详解】底面直径是10,则底面圆周长,
即圆锥的展开图(如下图所示)中,弧的长度为,
母线cm,故圆心角,
当绳子是线段时,绳子长度最短,
在Rt中,.
故绳子的长度为cm.
23.(1)
(2)
【分析】(1)利用扇形弧长公式列等式,代入即可得到;
(2)利用扇形的面积公式和三角形面积公式求面积即可.
(1)
依题意可得,,若,则.
(2)
因为扇形的面积为()
所以两个正三角形的面积之和为(),
故.
一、单选题
1.与角终边相同的角可以表示为( )
A. B.
C. D.
2.早在两千年前,古人就通过观测发现地面是球面,并会运用巧妙的方法对地球半径进行估算.如图所示,把太阳光视为平行光线,O为地球球心,A,B为北半球上同一经度的两点,且A,B之间的经线长度为L,于同一时刻在A,B两点分别竖立一根长杆和,通过测量得到两根长杆与太阳光的夹角和(和的单位为弧度),由此可计算地球的半径为( )
A. B. C. D.
3.圆心在原点,半径为10的圆上的两个动点M,N同时从点出发,沿圆周运动,点M按逆时针方向旋转,速度为弧度/秒,点N按顺时针方向旋转,速度为弧度/秒,则它们第三次相遇时点M转过的弧度数为( )
A. B. C. D.
4.若是锐角,则,是( )
A.第一象限角 B.第三象限角
C.第一象限角或第三象限角 D.第二象限角或第四象限角
5.“角a与β的终边关于直线对称”是“”的( )
A.充分必要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
6.一个扇形的弧长与面积的数值都是3,则该扇形圆心角的弧度数为( )
A. B. C. D.2
7.已知扇形的面积为8,且圆心角弧度数为2,则扇形的周长为( )
A.32 B.24 C. D.
8.如今我们在测量视力的时候,常用对数视力表(如图),视力值从4.0到5.3,每行相差0.1,这种计算视力的方法称为五分记录法,“对数视力表”和“五分记录法”是由我国著名眼科专家缪天荣(1914—2005)在1959年研制发明的,这种独创的视力表的核心在于:将视力和视角设定为对数关系,因此被认为是一种最符合视力生理的,而又便于统计和计算的视力检测系统,这使中国的眼科研究一下子站到了世界的巅峰,1986年,《对数视力表》在第25届国际眼科大会(罗马)宣读,引起轰动,1990年《标准对数视力表》被制定为国家标准(GB11533—89),并在全国实施.已知在五分记录法中,规定视力值,其中为人眼的视角,单位为分(1度=60分),视角的大小,决定了人眼能看到的最小物体的长度,这个长度约等于以眼球为圆心(眼球大小忽略不计),视角为圆心角,眼球与物体之间的距离为半径的扇形的弧长.如果某人的一只眼睛的视力值为4.7,那么这只眼睛能看到距离5米外的最小物体的长度约为(参考数据:,)( )
A.1.5毫米 B.2.9毫米 C.4.4毫米 D.5.8毫米
9.已知扇形的周长是6cm,面积是,则扇形的中心角的弧度数是( )
A.1 B.4 C.1或4 D.2或4
10.如图所示的时钟显示的时刻为4:30,设半个小时后时针与分针的夹角为,则( )
A. B. C. D.
11.已知集合,则下列选项正确的是( )
A. B. C. D.
12.折扇是我国传统文化的延续,在我国已有四千年左右的历史,“扇”与“善”谐音,折扇也寓意“善良”“善行”.它常以字画的形式体现我国的传统文化,也是运筹帷幄、决胜千里、大智大勇的象征(如图1),图2为其结构简化图,设扇面A,B间的圆弧长为l,AB间的弦长为d,圆弧所对的圆心角为(为弧度角),则l、d和所满足的恒等关系为( ).
A. B.
C. D.
13.已知点,则角的终边在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
14.若={α|,B={第一或第四象限角},则A、B关系为( )
A.A=B B.AB C.AB D.非A、B、C结论
15.如图是一个近似扇形的湖面,其中,弧的长为.为了方便观光,欲在两点之间修建一条笔直的走廊.若当时,,扇形的面积记为,则的值约为( )
A. B.
C. D.
二、填空题
16.古代文人墨客与丹青手都善于在纸扇上题字题画,题字题画的部分多为扇环.已知某扇形的扇环如图所示,其中外弧线的长为,内弧线的长为,连接外弧与内弧的两端的线段均为,则该扇形的中心角的弧度数为____________.
17.鲁洛克斯三角形是一种特殊的三角形,指分别以正三角形的顶点为圆心,以其边长为半径作圆弧,由这三段圆弧组成的曲边三角形.它的特点是:在任何方向上都有相同的宽度,机械加工业上利用这个性质,把钻头的横截面做成鲁洛克斯三角形的形状,就能在零件上钻出正方形的孔来.如图,已知某鲁洛克斯三角形的一段弧的长度为,则该鲁洛克斯三角形的面积为______.
18.如图,正五边形的边长为5,分别以点C、D为圆心,长为半径画弧,两弧交于点F,则的长为_____.
19.某城市一圆形空地的平面图如图所示,为了方便市民休闲健身,政府计划在该空地建设运动公园(图中阴影部分).若是以B为直角的等腰直角三角形,,则该公园的面积为________.
20.已知圆锥的底面半径为2,其侧面展开扇形的圆心角大小为,则这个圆锥的母线长为______.
三、解答题
21.(1)写出与终边相同的角的集合S,并把S中适合不等式的元素α写出来:
(2)已知扇形AOB的周长为8,面积为3,求圆心角的大小;
22.有一个圆锥形漏斗,其底面直径是10cm,母线长为20cm,在漏斗口的点处用一根绳子将漏斗挂在墙面上,当绳子的长度最短时,可以紧紧地箍住漏斗,不会上下滑动,求此时绳子的长度.
23.如图,一图形由一个扇形与两个正三角形组成,其中扇形的周长为,圆心角的弧度数为,半径为.
(1)若,求;
(2)设该图形的面积为,写出关于的函数表达式.
参考答案:
1.A
【分析】先求出相近的终边相同的角,即可判断.
【详解】与角终边相同的角为,故与角终边相同的角可以表示为.
故选:A
2.A
【分析】过点B作太阳光的平行线,与 的延长线交于点C,可求出,利用弧长公式即可求得地球的半径.
【详解】如图所示,过点B作太阳光的平行线,与 的延长线交于点C,
则 , ,所以,
设地球半径为R,则根据弧长公式得 ,所以 ,
故选:A.
3.C
【分析】根据两点相遇一次转过弧度之和为即可求解.
【详解】由题意,动点第三次相遇,则两个动点转过的弧度之和为:,
设从点出发秒后点第三次相遇,则,解得秒,
此时点转过的弧度数为弧度
故选:C
4.C
【分析】根据取奇数和偶数分类讨论即可求解.
【详解】是锐角,,,当k为奇数时,为第三象限角;当k为偶数时,为第一象限角.所以为第一象限角或第三象限角.
故选:C.
5.C
【分析】根据终边关于对称,得两角的关系,再由,得两角满足的关系,根据充分必要条件的定义即可求解.
【详解】角与的终边关于直线对称,则,
.
反之,当时,则,从而角a与β的终边不一定关于直线对称.
故“角与的终边关于直线对称”是“”的充分不必要条件.
故选:C
6.C
【分析】由扇形的弧长公式和面积公式列方程组求解.
【详解】设扇形的圆心角的弧度数为α,半径为r,则解得
故选:C.
7.D
【分析】根据扇形面积和弧长公式即可求解.
【详解】圆心角,扇形面积,
即,得半径,
所以弧长,
故扇形的周长.
故选:D
8.B
【分析】由视力值求出视角,再由计算出弧长即得.
【详解】由题意得,解得分,则圆心角为2分,半径为5米的扇形的弧长等于米=2.9毫米.
故选:B.
9.C
【分析】根据给定条件,利用扇形面积公式求出扇形所在圆半径,再借助弧长公式求解作答.
【详解】设扇形所在圆半径为r,则扇形弧长为,依题意,,解得或,
所以扇形的中心角的弧度数是或.
故选:C
10.B
【分析】由题意,根据时钟的特性,结合弧度制的写法,可得答案.
【详解】半小时后是5:00整,时针指向5,分针指向12,.
故选:B.
11.B
【分析】可确定在上集合和集合的关系,然后结合角的周期性得结论.
【详解】在范围,集合含有,集合含有,
由角的周期性变化可知:,
故选:B.
12.A
【分析】利用弧长公式及直角三角形中的正弦公式,化简即可得到答案.
【详解】解:设扇形的半径为R,如图,由弧长公式,得,在直角三角形中,
化简得.
故选:A.
13.B
【分析】根据象限角概念求解即可.
【详解】因为,所以的终边在第二象限.
故选:B
14.D
【分析】在集合与中举例说明即可判断.
【详解】集合中,若,不属于第一或第四象限角,即.
集合中,若,是第一象限角,但.
综上,集合与没有关系.
故选:D
15.B
【分析】由题可得,再根据扇形面积公式可得,结合条件即得.
【详解】设扇形的圆心角为,则,
在中,,
又,
∴,又,
∴.
故选:B.
16.
【分析】根据扇形弧长与扇形的中心角的弧度数为的关系,可求得,进而可得该扇形的中心角的弧度数.
【详解】解:如图,
依题意可得弧的长为,弧的长为,设扇形的中心角的弧度数为
则,则,即.
因为,所以,所以该扇形的中心角的弧度数.
故答案为:.
17.
【分析】由弧长公式可求得等边的边长,再根据该鲁洛克斯三角形的面积等于三个扇形的面积减去2个的面积,结合扇形和三角形的面积公式即可得解.
【详解】解:由题意可知,
设,
则弧的长度为,所以,
设弧所对的扇形的面积为,
,
则该鲁洛克斯三角形的面积为.
故答案为:.
18.
【分析】本题关键在于如何得到所对圆心角,利用圆半径得到为等边三角形得出,再利用正多变形内角,从而得出,然后代入公式即可得出答案.
【详解】连接,,由题可得,
则是等边三角形,
,
在正五边形中,,
,
的长,
故答案为:.
19.
【分析】利用扇形面积公式即可得到结果.
【详解】由题可知圆心为的中点,,连接,
该公园的面积
故答案为:
20.12
【分析】设母线长为,由弧长公式计算可得;
【详解】解:设母线长为,则侧面展开的扇形的弧长为,
由题意,即,因为,故.
故答案为:
21.(1),;(2)6或.
【分析】(1)由终边相同的角的表示直接得,对取值得符合条件得角;
(2)由扇形面积公式与弧长公式求解即可
【详解】(1)与角终边相同的角的集合为,
当时,时,时,;
中适合不等式的元素为:;
(2)设扇形的半径为,中心角为,则.
由题意可得:,
又.
联立解得或.
22.cm
【分析】由圆锥的展开图可知,绳子是线段时,绳子长度最短,根据扇形弧长公式可求圆心角,从而可求弦的长度.
【详解】底面直径是10,则底面圆周长,
即圆锥的展开图(如下图所示)中,弧的长度为,
母线cm,故圆心角,
当绳子是线段时,绳子长度最短,
在Rt中,.
故绳子的长度为cm.
23.(1)
(2)
【分析】(1)利用扇形弧长公式列等式,代入即可得到;
(2)利用扇形的面积公式和三角形面积公式求面积即可.
(1)
依题意可得,,若,则.
(2)
因为扇形的面积为()
所以两个正三角形的面积之和为(),
故.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
