15.3 分式方程(2)课件(共25张PPT)
文档属性
| 名称 | 15.3 分式方程(2)课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
人教版 八年级上册
15. 3分式方程 (2)
教学目标:
1.能够列分式方程解决简单的实际问题.
2.通过学习分式方程的解法,体会转化的数学思想.
教学重点:分式方程的解法.
课件说明
(1)去分母,将分式方程转化为整式方程;
(2)解转化所得的整式方程;
(3)检验.
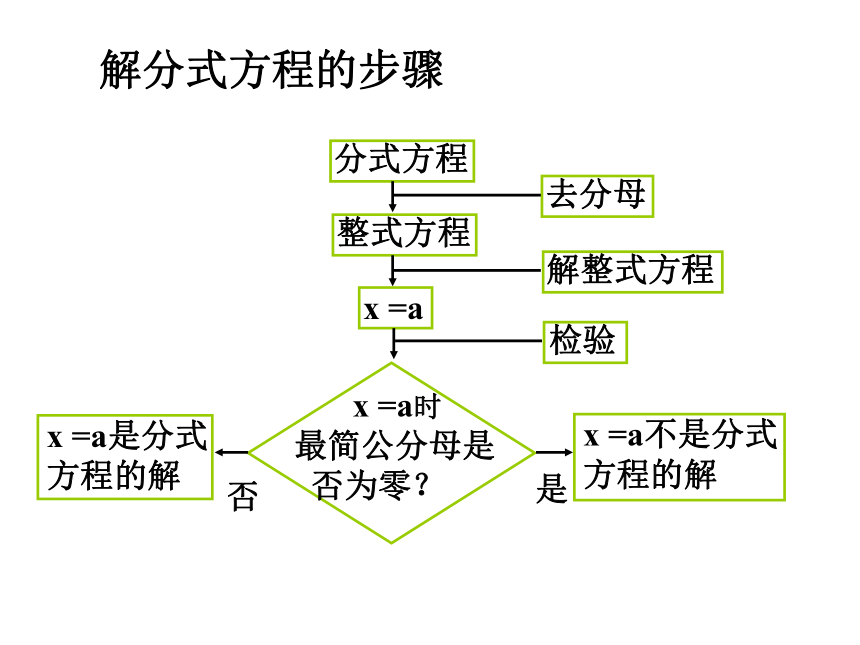
解分式方程的步骤:
复习旧知
分式方程
整式方程
去分母
解整式方程
x =a
检验
x =a是分式
方程的解
x =a不是分式
方程的解
x =a时
最简公分母是
否为零?
否
是
解分式方程的步骤
1.分式方程 的解为( ).
A.x=2 B.x=-2 C.x=1 D.x=-1
2.已知关于x的分式方程 的解
为x=2,则k的值为 ( ).
A. -2 B.2 C1 D. -1
复习旧知
1
x+2
=1
x
x- 1
-
A
A
1
3-x
=1
k
x- 3
-
3.当x= 时,
1
x-2
=1.
3
4.分式方程 的解为 .
1
2x-2
x
x- 1
=
x=
1
2
移项,合并同类项,得
解:方程两边乘以(x+1)(x-1) ,约去分母,得
2(x+1)
去括号,得
2x+2=.
系数化为1,得
x=1 .
2x=2.
检验:
当x=1 时,
(x+1)(x-1)=0.
x=1不是原分式方程的解.
∴
5.解方程:
x-1
2
=
x2-1
4
原分式方程无解.
∴
=4.
移项,合并同类项,得
解:方程两边乘以 x(x+1)(x-1),约去分母,得
5(x-1)
去括号,得
5x-5-x-1=0.
系数化为1,得
x=
4x=6.
检验:
当x= 时,
x(x+1)(x-1)≠0.
∴x= 是原分式方程的解.
6.解方程:
x2+x
5
=0
x2-x
1
-
-
(x+1)
=0.
3
2
3
2
3
2
设乙队单独施工1个月能完成总工程的 , 则乙队半个月完成总工程的 , 两队半个月完成总工程的 .
例 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
(1)甲队1个月完成总工程的___,那么甲队半个月
完成总工程的 ;
1
3
1
x
1
6
1
2x
1
6
+
1
2x
例题解析
问题中的哪个等量关系可以用来列方程?
例 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
甲队单独施工1个月完成总工程的三分之一,甲乙两队又共同工作了半个月,总工程全部完成.
解:设乙队单独施工1个月能完成总工程的 ,
记总工程量为1,根据工程的实际进度,得
例 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
1
x
1
3
+
1
6
+
1
2x
=
1
解:设乙队单独施工1个月能完成总工程的 ,
记总工程量为1,根据工程的实际进度,得
方程两边同乘6x,约去分母得
1
x
1
3
+
1
6
+
1
2x
=
1
2x
解这个方程得
检验:当x =1时6x ≠0,
由上可知,若乙队单独工作1个月可以完成全部任务,对比甲队1个月完成任务的 ,可知乙队施工速度快.
x =1
x =1是原分式方程的解.
1
3
+x
+ 3
=
6x
某车间有甲、乙两个小组,甲组的工作效率比乙组工作效率高25%,因此甲组加工2 000个零件所用的时间比乙组加工1 800个零件所用的时间少半小时,问甲、乙两组每小时各加工多少个零件
设乙组每小时加工x个零件,
则甲组每小时加工零件
1.25x个,
根据题意,得
1800
x
2000
1.25x
=
-
1
2
解:
练习巩固
1800
x
2000
1.25x
=
-
1
2
1800
x
1600
x
=
-
1
2
=
1
2
200
x
x=
400
方程求解过程
练习 某车间有甲、乙两个小组,甲组的工作效
率比乙组工作效率高25%,因此甲组加工2 000个零件
所用的时间比乙组加工1 800个零件所用的时间少半小
时,问甲、乙两组每小时各加工多少个零件?
设乙组每小时加工x个零件,
则甲组每小时加工零件,
1.25x个,
根据题意,得
1800
x
2000
1.25x
=
-
1
2
解这个方程得
当x =400时,1.25x =500.
x =400
经检验x =400是原分式方程的解.
答:甲组每小时加工500个零件,
乙组每小时加工400个零件.
解:
(1) 本节课学习了哪些主要内容?
(2) 解分式方程的一般步骤有哪些?关键是什么?
解方程的过程中要注意的问题有哪些?
(3)列分式方程解应用题的步骤是什么?与列整式
方程解应用题的过程有什么区别和联系?
课堂小结
列分式方程解决实际问题的一般步骤:
(1)审:弄清题目中的已知量和未知量,并能找出表示
问题含义的全部等量关系;
(2)设:直接或间接设未知数,并用所设的未知数表示
有关的量;
(3)列:找出相等关系,列出分式方程.
(4)解:解所列分式方程;
(5)验:既要检验未知数值是否为原分式方程的根,还要
检验是否符合实际意义.
(6)答:给出问题的最后答案,注意不要忘记答案的单位.
1.“爱劳动,劳动美.”甲、乙两同学同时从家里出发,分别到距家6km和10 km 的实践基地参 加劳动.若甲、乙的速度比是3:4,结果甲比乙提前 20 min到达基地,求甲、乙的速度,设甲的速度为3x km/h,则依题意可列方程为 ( ).
巩固提高
A. B.
C. D.
6
3x
+
1
3
=
10
4x
6
3x
+
20
=
10
4x
6
3x
-
1
3
=
10
4x
6
3x
-
20
=
10
4x
A
2.甲、乙两人做某种机械零件,已知每小时甲比乙多做6个,甲做90个所用的时间和乙做60个所用的时间相等,设乙每小时做x个零件,以下所列方程正确的是 ( ).
A. B.
C. D.
60
x+6
x
90
=
60
x+6
x
90
=
60
x-6
x
90
=
60
x-6
x
90
=
C
3.某市工业试验区投资50760万元开发了多个项目,今后还将投资106960万元开发多个新项目,每个新项目平均投资比今年每个项目平均投资多500万元,并且新增项目数量比今年多20个,假设今年每个项目平均投资是x万元,那么下列方程符合题意的是( ).
x+20
106960
-
x
50760
=500
C.
x+500
106960
-
x
50760
=500
D.
x+500
106960
-
x
50760
=20
A.
x+500
106960
-
x
50760
=20
B.
A
4.已知购买足球的数量是篮球的2倍,购买足球用了5000元,购买篮球用了4000元,篮球单价比足球贵30元.
根据题意可列方程
则方程中x表示( ).
A.足球的单价 B.篮球的单价
C.足球的数量 D.篮球的数量
4000
x
=
2x
5000
-
30.
D
5.对某款电动汽车和某款燃油车的对比调查发现,电动汽车平均每公里的充电费比燃油车平均每公里的加油费少0.6元.若充电费和加油费均为200元时,电动汽车可行驶的总路程是燃油车的4倍,求这款电动汽车平均每公里的充电费.
解:设这款电动汽车平均每公里的充电费为x元, 根据题意,得
经检验,x=0.2 是原方程的根,且符合题意.
答:这款电动汽车平均每公里的充电费为0.2 元.
200
x+0.6
x
200
=
解得 x=0.2,
●4
今天作业
课本P154页第3题
课本P154页第1题(5)~(8)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八年级上册
15. 3分式方程 (2)
教学目标:
1.能够列分式方程解决简单的实际问题.
2.通过学习分式方程的解法,体会转化的数学思想.
教学重点:分式方程的解法.
课件说明
(1)去分母,将分式方程转化为整式方程;
(2)解转化所得的整式方程;
(3)检验.
解分式方程的步骤:
复习旧知
分式方程
整式方程
去分母
解整式方程
x =a
检验
x =a是分式
方程的解
x =a不是分式
方程的解
x =a时
最简公分母是
否为零?
否
是
解分式方程的步骤
1.分式方程 的解为( ).
A.x=2 B.x=-2 C.x=1 D.x=-1
2.已知关于x的分式方程 的解
为x=2,则k的值为 ( ).
A. -2 B.2 C1 D. -1
复习旧知
1
x+2
=1
x
x- 1
-
A
A
1
3-x
=1
k
x- 3
-
3.当x= 时,
1
x-2
=1.
3
4.分式方程 的解为 .
1
2x-2
x
x- 1
=
x=
1
2
移项,合并同类项,得
解:方程两边乘以(x+1)(x-1) ,约去分母,得
2(x+1)
去括号,得
2x+2=.
系数化为1,得
x=1 .
2x=2.
检验:
当x=1 时,
(x+1)(x-1)=0.
x=1不是原分式方程的解.
∴
5.解方程:
x-1
2
=
x2-1
4
原分式方程无解.
∴
=4.
移项,合并同类项,得
解:方程两边乘以 x(x+1)(x-1),约去分母,得
5(x-1)
去括号,得
5x-5-x-1=0.
系数化为1,得
x=
4x=6.
检验:
当x= 时,
x(x+1)(x-1)≠0.
∴x= 是原分式方程的解.
6.解方程:
x2+x
5
=0
x2-x
1
-
-
(x+1)
=0.
3
2
3
2
3
2
设乙队单独施工1个月能完成总工程的 , 则乙队半个月完成总工程的 , 两队半个月完成总工程的 .
例 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
(1)甲队1个月完成总工程的___,那么甲队半个月
完成总工程的 ;
1
3
1
x
1
6
1
2x
1
6
+
1
2x
例题解析
问题中的哪个等量关系可以用来列方程?
例 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
甲队单独施工1个月完成总工程的三分之一,甲乙两队又共同工作了半个月,总工程全部完成.
解:设乙队单独施工1个月能完成总工程的 ,
记总工程量为1,根据工程的实际进度,得
例 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
1
x
1
3
+
1
6
+
1
2x
=
1
解:设乙队单独施工1个月能完成总工程的 ,
记总工程量为1,根据工程的实际进度,得
方程两边同乘6x,约去分母得
1
x
1
3
+
1
6
+
1
2x
=
1
2x
解这个方程得
检验:当x =1时6x ≠0,
由上可知,若乙队单独工作1个月可以完成全部任务,对比甲队1个月完成任务的 ,可知乙队施工速度快.
x =1
x =1是原分式方程的解.
1
3
+x
+ 3
=
6x
某车间有甲、乙两个小组,甲组的工作效率比乙组工作效率高25%,因此甲组加工2 000个零件所用的时间比乙组加工1 800个零件所用的时间少半小时,问甲、乙两组每小时各加工多少个零件
设乙组每小时加工x个零件,
则甲组每小时加工零件
1.25x个,
根据题意,得
1800
x
2000
1.25x
=
-
1
2
解:
练习巩固
1800
x
2000
1.25x
=
-
1
2
1800
x
1600
x
=
-
1
2
=
1
2
200
x
x=
400
方程求解过程
练习 某车间有甲、乙两个小组,甲组的工作效
率比乙组工作效率高25%,因此甲组加工2 000个零件
所用的时间比乙组加工1 800个零件所用的时间少半小
时,问甲、乙两组每小时各加工多少个零件?
设乙组每小时加工x个零件,
则甲组每小时加工零件,
1.25x个,
根据题意,得
1800
x
2000
1.25x
=
-
1
2
解这个方程得
当x =400时,1.25x =500.
x =400
经检验x =400是原分式方程的解.
答:甲组每小时加工500个零件,
乙组每小时加工400个零件.
解:
(1) 本节课学习了哪些主要内容?
(2) 解分式方程的一般步骤有哪些?关键是什么?
解方程的过程中要注意的问题有哪些?
(3)列分式方程解应用题的步骤是什么?与列整式
方程解应用题的过程有什么区别和联系?
课堂小结
列分式方程解决实际问题的一般步骤:
(1)审:弄清题目中的已知量和未知量,并能找出表示
问题含义的全部等量关系;
(2)设:直接或间接设未知数,并用所设的未知数表示
有关的量;
(3)列:找出相等关系,列出分式方程.
(4)解:解所列分式方程;
(5)验:既要检验未知数值是否为原分式方程的根,还要
检验是否符合实际意义.
(6)答:给出问题的最后答案,注意不要忘记答案的单位.
1.“爱劳动,劳动美.”甲、乙两同学同时从家里出发,分别到距家6km和10 km 的实践基地参 加劳动.若甲、乙的速度比是3:4,结果甲比乙提前 20 min到达基地,求甲、乙的速度,设甲的速度为3x km/h,则依题意可列方程为 ( ).
巩固提高
A. B.
C. D.
6
3x
+
1
3
=
10
4x
6
3x
+
20
=
10
4x
6
3x
-
1
3
=
10
4x
6
3x
-
20
=
10
4x
A
2.甲、乙两人做某种机械零件,已知每小时甲比乙多做6个,甲做90个所用的时间和乙做60个所用的时间相等,设乙每小时做x个零件,以下所列方程正确的是 ( ).
A. B.
C. D.
60
x+6
x
90
=
60
x+6
x
90
=
60
x-6
x
90
=
60
x-6
x
90
=
C
3.某市工业试验区投资50760万元开发了多个项目,今后还将投资106960万元开发多个新项目,每个新项目平均投资比今年每个项目平均投资多500万元,并且新增项目数量比今年多20个,假设今年每个项目平均投资是x万元,那么下列方程符合题意的是( ).
x+20
106960
-
x
50760
=500
C.
x+500
106960
-
x
50760
=500
D.
x+500
106960
-
x
50760
=20
A.
x+500
106960
-
x
50760
=20
B.
A
4.已知购买足球的数量是篮球的2倍,购买足球用了5000元,购买篮球用了4000元,篮球单价比足球贵30元.
根据题意可列方程
则方程中x表示( ).
A.足球的单价 B.篮球的单价
C.足球的数量 D.篮球的数量
4000
x
=
2x
5000
-
30.
D
5.对某款电动汽车和某款燃油车的对比调查发现,电动汽车平均每公里的充电费比燃油车平均每公里的加油费少0.6元.若充电费和加油费均为200元时,电动汽车可行驶的总路程是燃油车的4倍,求这款电动汽车平均每公里的充电费.
解:设这款电动汽车平均每公里的充电费为x元, 根据题意,得
经检验,x=0.2 是原方程的根,且符合题意.
答:这款电动汽车平均每公里的充电费为0.2 元.
200
x+0.6
x
200
=
解得 x=0.2,
●4
今天作业
课本P154页第3题
课本P154页第1题(5)~(8)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
