21.6 综合与实践 获取最大利润 课件(共25张PPT)
文档属性
| 名称 | 21.6 综合与实践 获取最大利润 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 939.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 08:41:16 | ||
图片预览








文档简介
(共25张PPT)
沪科版 九年级上册
21.6综合与实践获取最大利润
教学目标:
1.会结合实际问题建立二次函数模型解决简单的实际问题.
2.学会分析问题、解决问题的一般方法.
教学重点:
会结合实际问题建立二次函数模型,知道函数建模的一般步骤和方法.
教学难点:
应用二次函数模型解决最大利润问题.
复习旧知
1.利润的基本公式
(1)利润=收入-成本
(2)利润=每件的利润×总件数
每件的利润=
售价-进价
2.二次函数y=ax2+bx+c(a ≠ 0)的最值确定
若(1)a>0,
b
2a
-
y最小值= .
4ac-b2
4a
当x= 时,
若(1)a<0,
y最大值= .
4ac-b2
4a
当x= 时,
b
2a
-
3.二次函数y=a(x+h)2+k (a ≠ 0)的最值确定
若(1)a>0,
当x=-h 时,
y最小值=k .
若(2)a<0,
当x=-h 时,
y最大值=k .
函数建模过程一般步骤
函数模型的建立建立两个变量之间的函数模型可以通过以下几个步骤来完成:
(1)建立适当的平面直角坐标系,以问题中自变量的值为横坐标,对应的函数值为纵坐标,在平面直角坐标系内描出相应的点若干个.
(2)观察描出的点在平面直角坐标系内的分布情况,从而推测函数图象的大致形状,结合已学函数知识进一步猜想y与工之间的函数关系的类型.
(3)根据猜想及已知条件,用待定系数法求出函数表达式并检验必要时可对所求表达式作适当修正.
(4)运用求得的函数表达式解决相关问题.
1.某商品现在的售价为每件60 元,每星期可卖
出300件.市场 调查反映,如果调整商品售价,
每降价1元,每星期可多卖出20件.设每件商品
降价x元后,每星期售出商品的总销售额为 y元,
则y与x之间的函数关系式为 ( ).
A.y=60(300+20x) B.y=(60-x)(300+20x)
C.y=300(60 -20x) D.y=(60-x)(300-20x)
B
2.学校商店销售一种练习本所获得的总利润
y(元)与销售单价x(元)之间的函数关系式为
y=-2(x-2)2+48,则下列叙述正确的是( ).
A.当x=2时,利润取最大值48元
B.当x=-2时,利润取最大值48元
C.当x=2时,利润取最小值48元
D.当x=-2时,利润取最小值48元
A
3.一件工艺品的进价为100元,标价135元出售,
每天可售出100件,根据销售统计,一件工艺
品每降价1元,则每天可多售出4件,要使每天
获得的利润最大,则每件需降价( ).
A.3.6元 B.5元 C.10元 D.12元
B
列出关于利润的二次函数关系式和求出顶点
坐标是解题的关键,要注意自变量的取值范围.
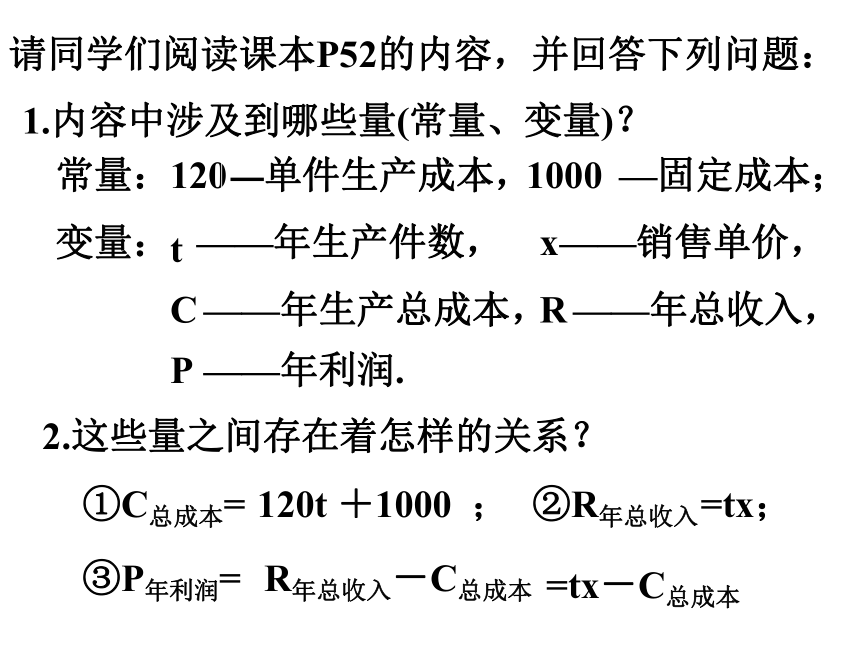
请同学们阅读课本P52的内容,并回答下列问题:
1.内容中涉及到哪些量(常量、变量)?
常量:
120
—单件生产成本,
1000
—固定成本;
变量:
t
——年生产件数,
x
——销售单价,
C
——年生产总成本,
R
——年总收入,
P
——年利润.
2.这些量之间存在着怎样的关系?
③P年利润=
①C总成本=
②R年总收入
=tx;
=tx-C总成本
R年总收入-C总成本
120t +1000 ;
当一个工厂在决定是否要生产某种产品时,往往向市场分析专家咨询该产品的销路,一种产品的销售量通常与销售单价有关,当单价上涨时,销售量就下降.假设某市场分析专家提供了下列数据:
设生产t件该产品的成本为:
销售单价x/元 50 100 150 300
年销售量t/件 5000 4000 3000 0
课本P52~53问题①
完成下列要求:
(1)在下图中,描出上述表格中的各组数据对应的点;
例题解析
C=50t+1000
O
t/件
x/元
50
100
150
200
250
300
1000
2000
3000
4000
5000
(2)描出的这些点在一条直线上吗?
销售单价x/元 50 100 150 300
年销售量t/件 5000 4000 3000 0
·
·
·
·
∴ t=-20x+6000
设t=kx+b,
50k+b=5000
100k+b=4000
∴k=-20,
b=6000
则有
求t和x之间的函数表达式;
(3)问当销售单价x和年销售量t各为多少时,年利润最大?
=-20x +6000x-50t-1000
解:∵R年总收入=t ·x,
∴P年利润=(-20x+6000)·x -(50t+1000)
=-20x +6000x-50(-20x+6000)-1000
=-20x +6000x+1000x-300000-1000
=-20x +7000x-301000
C成本=50t+1000,
t=-20x+6000,
此时年销售量t=-20×175+6000=2500.
P年利润=
=tx-C总成本
R年收入-C总成本
∵a= -20<0,
∴P年利润有最大值,
b
2a
-
且当x= =-
7000
2×(-20)
P值最大.
=175时,
年销售量t/件 750 3000 5096 8500 9417
销售单价x/元 3850 3400 3000 2300 2100
问题②设生产t件某种电子产品的成本(单位:元)可以近似地表示为:
C=1000t+2 000 000.
制造商为了获得最大利润,进行了市场调查,取得了该种电子产品销售单价x和年销售量t之间的一组数据:
(1)在下图中,描出上述表格中的各组数据对应的点;
请你帮助制造商分析,当年销售量t和销售单价x
分别是多少时,年利润P最大?
年销售量t/件 750 3000 5096 8500 9417
销售单价x/元 3850 3400 3000 2300 2100
·
·
·
·
·
O
t/件
x/元
1000
2000
3000
4000
5000
6000
2000
2500
3000
3500
4000
7000
8000
9000
10000
请你帮助制造商分析,当年销售量t和销售单价x
分别是多少时,年利润P最大?
年销售量t/件 750 3000 5096 8500 9417
销售单价x/元 3850 3400 3000 2300 2100
∴ t=-5x+20000
设t=kx+b,
3850k+b=750
3400k+b=3000
∴k=-5,
b=20000
则有
O
t/件
x/元
1000
2000
3000
4000
5000
6000
2000
2500
3000
3500
4000
7000
8000
9000
10000
(2)当销售单价x和年销售量t各为多少时,年利润最大?
=-5x +20000x-1000t-2000000
解:∵R年总收入=t ·x,
∴P年利润=(-5x+20000)·x -(1000t+2000000)
=-5x +20000x-1000(-5x+20000)-2000000
=-5x +20000x+5000x-30000000-2000000
=-5x +25000x-32000000
C成本=1000t+2000000,
t=-5x+20000,
此时年销售量t=-5×2500+20000=7500.
P年利润=
=tx-C总成本
R年收入-C总成本
∵a= -5<0,
∴P年利润有最大值,
b
2a
-
且当x= =-
25000
2×(-5)
P值最大.
=2500时,
课堂小结
运用二次函数解决实际问题的方法和步骤:
①首先判断问题中的两个变量之间是否满足二次函数关系;
②当确定两个变量是二次函数关系时,用含自变量的代数式表示相关的量;
③根据给出的数据确定函数的表达式和自变量的取值范围
④运用二次函数的有关性质结合自变量的实际意义计算最大(或最小)利润.
九(1)班数学兴趣小组经过市场调查,整理出某商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表
已知该商品的进价为每件30元,设销售该商品每天的 利润为y元.(1)求出y与x的函数表达式;(2)问销售该商品第几天时,当天销售利润最大 最大利润是多少 (3)该商品在销售过程中,共有多少天每天销售利润不低于4800元
请直接写出结果.
巩固提高
时间
每天销量/件
200-2x
售价(元/件)
x+40
1≤x<50
50≤x≤90
时间 x/天
90
九(1)班数学兴趣小组经过市场调查,整理出某商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表
时间
每天销量/件
200-2x
售价(元/件)
x+40
1≤x≤50
50≤x≤90
时间 x/天
90
(1)根据每件利润乘每天销量可得每天利润;
(2)根据分段函数和二次函数、一次函数的性质,
分别得出最值,再比较可得出答案;
(3)根据函数值大于或等于4800可得不等式,
解不等式即可.
分析:
解:(1)当1≤x<50时,
y=(200-2x)(x+40-30)
=-2x2+180x+2000
当50≤x≤90时,
y=(200-2x)(90-30)
=-120x+12000
∴y=
-2x2+180x+2000
-120x+12000
(1≤x<50)
(50≤x≤90)
b
2a
-
且当x= =-
180
2×(-2)
y值最大.
=45时,
y最大值=-2×452+180×45+2000=6050;
∴此二次函数有最大值,
∵一次函数y=-120x+12000的k=-120<0,
(2) 当1≤x<50时,
∵ 二次函数y=-2x2+180x+2000的a=-2<0,
当50≤x≤90时,
∴y随x的增大而减小,
∴当x=50时,y最大值=6000.
综上所述,销售该商品第45天时,当天销售利润最大,最大利润是 6050 元.
(3)当1≤x<50时,
-2x2 +180x+2000≥4800,解得20≤x<30;
当50≤x≤90时,
-120x+12000≥4800,解得 50≤x≤60.
综上所述,当20≤x≤60时,即共有41天每天销售利润不低于4800元.
经验总结:
对于二次函数的应用,先利用“每件利润x每天销量
=每天利润”求函数表达式,再利用函数的性质求最值.
今天作业
课本P58页第11题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
21.6综合与实践获取最大利润
教学目标:
1.会结合实际问题建立二次函数模型解决简单的实际问题.
2.学会分析问题、解决问题的一般方法.
教学重点:
会结合实际问题建立二次函数模型,知道函数建模的一般步骤和方法.
教学难点:
应用二次函数模型解决最大利润问题.
复习旧知
1.利润的基本公式
(1)利润=收入-成本
(2)利润=每件的利润×总件数
每件的利润=
售价-进价
2.二次函数y=ax2+bx+c(a ≠ 0)的最值确定
若(1)a>0,
b
2a
-
y最小值= .
4ac-b2
4a
当x= 时,
若(1)a<0,
y最大值= .
4ac-b2
4a
当x= 时,
b
2a
-
3.二次函数y=a(x+h)2+k (a ≠ 0)的最值确定
若(1)a>0,
当x=-h 时,
y最小值=k .
若(2)a<0,
当x=-h 时,
y最大值=k .
函数建模过程一般步骤
函数模型的建立建立两个变量之间的函数模型可以通过以下几个步骤来完成:
(1)建立适当的平面直角坐标系,以问题中自变量的值为横坐标,对应的函数值为纵坐标,在平面直角坐标系内描出相应的点若干个.
(2)观察描出的点在平面直角坐标系内的分布情况,从而推测函数图象的大致形状,结合已学函数知识进一步猜想y与工之间的函数关系的类型.
(3)根据猜想及已知条件,用待定系数法求出函数表达式并检验必要时可对所求表达式作适当修正.
(4)运用求得的函数表达式解决相关问题.
1.某商品现在的售价为每件60 元,每星期可卖
出300件.市场 调查反映,如果调整商品售价,
每降价1元,每星期可多卖出20件.设每件商品
降价x元后,每星期售出商品的总销售额为 y元,
则y与x之间的函数关系式为 ( ).
A.y=60(300+20x) B.y=(60-x)(300+20x)
C.y=300(60 -20x) D.y=(60-x)(300-20x)
B
2.学校商店销售一种练习本所获得的总利润
y(元)与销售单价x(元)之间的函数关系式为
y=-2(x-2)2+48,则下列叙述正确的是( ).
A.当x=2时,利润取最大值48元
B.当x=-2时,利润取最大值48元
C.当x=2时,利润取最小值48元
D.当x=-2时,利润取最小值48元
A
3.一件工艺品的进价为100元,标价135元出售,
每天可售出100件,根据销售统计,一件工艺
品每降价1元,则每天可多售出4件,要使每天
获得的利润最大,则每件需降价( ).
A.3.6元 B.5元 C.10元 D.12元
B
列出关于利润的二次函数关系式和求出顶点
坐标是解题的关键,要注意自变量的取值范围.
请同学们阅读课本P52的内容,并回答下列问题:
1.内容中涉及到哪些量(常量、变量)?
常量:
120
—单件生产成本,
1000
—固定成本;
变量:
t
——年生产件数,
x
——销售单价,
C
——年生产总成本,
R
——年总收入,
P
——年利润.
2.这些量之间存在着怎样的关系?
③P年利润=
①C总成本=
②R年总收入
=tx;
=tx-C总成本
R年总收入-C总成本
120t +1000 ;
当一个工厂在决定是否要生产某种产品时,往往向市场分析专家咨询该产品的销路,一种产品的销售量通常与销售单价有关,当单价上涨时,销售量就下降.假设某市场分析专家提供了下列数据:
设生产t件该产品的成本为:
销售单价x/元 50 100 150 300
年销售量t/件 5000 4000 3000 0
课本P52~53问题①
完成下列要求:
(1)在下图中,描出上述表格中的各组数据对应的点;
例题解析
C=50t+1000
O
t/件
x/元
50
100
150
200
250
300
1000
2000
3000
4000
5000
(2)描出的这些点在一条直线上吗?
销售单价x/元 50 100 150 300
年销售量t/件 5000 4000 3000 0
·
·
·
·
∴ t=-20x+6000
设t=kx+b,
50k+b=5000
100k+b=4000
∴k=-20,
b=6000
则有
求t和x之间的函数表达式;
(3)问当销售单价x和年销售量t各为多少时,年利润最大?
=-20x +6000x-50t-1000
解:∵R年总收入=t ·x,
∴P年利润=(-20x+6000)·x -(50t+1000)
=-20x +6000x-50(-20x+6000)-1000
=-20x +6000x+1000x-300000-1000
=-20x +7000x-301000
C成本=50t+1000,
t=-20x+6000,
此时年销售量t=-20×175+6000=2500.
P年利润=
=tx-C总成本
R年收入-C总成本
∵a= -20<0,
∴P年利润有最大值,
b
2a
-
且当x= =-
7000
2×(-20)
P值最大.
=175时,
年销售量t/件 750 3000 5096 8500 9417
销售单价x/元 3850 3400 3000 2300 2100
问题②设生产t件某种电子产品的成本(单位:元)可以近似地表示为:
C=1000t+2 000 000.
制造商为了获得最大利润,进行了市场调查,取得了该种电子产品销售单价x和年销售量t之间的一组数据:
(1)在下图中,描出上述表格中的各组数据对应的点;
请你帮助制造商分析,当年销售量t和销售单价x
分别是多少时,年利润P最大?
年销售量t/件 750 3000 5096 8500 9417
销售单价x/元 3850 3400 3000 2300 2100
·
·
·
·
·
O
t/件
x/元
1000
2000
3000
4000
5000
6000
2000
2500
3000
3500
4000
7000
8000
9000
10000
请你帮助制造商分析,当年销售量t和销售单价x
分别是多少时,年利润P最大?
年销售量t/件 750 3000 5096 8500 9417
销售单价x/元 3850 3400 3000 2300 2100
∴ t=-5x+20000
设t=kx+b,
3850k+b=750
3400k+b=3000
∴k=-5,
b=20000
则有
O
t/件
x/元
1000
2000
3000
4000
5000
6000
2000
2500
3000
3500
4000
7000
8000
9000
10000
(2)当销售单价x和年销售量t各为多少时,年利润最大?
=-5x +20000x-1000t-2000000
解:∵R年总收入=t ·x,
∴P年利润=(-5x+20000)·x -(1000t+2000000)
=-5x +20000x-1000(-5x+20000)-2000000
=-5x +20000x+5000x-30000000-2000000
=-5x +25000x-32000000
C成本=1000t+2000000,
t=-5x+20000,
此时年销售量t=-5×2500+20000=7500.
P年利润=
=tx-C总成本
R年收入-C总成本
∵a= -5<0,
∴P年利润有最大值,
b
2a
-
且当x= =-
25000
2×(-5)
P值最大.
=2500时,
课堂小结
运用二次函数解决实际问题的方法和步骤:
①首先判断问题中的两个变量之间是否满足二次函数关系;
②当确定两个变量是二次函数关系时,用含自变量的代数式表示相关的量;
③根据给出的数据确定函数的表达式和自变量的取值范围
④运用二次函数的有关性质结合自变量的实际意义计算最大(或最小)利润.
九(1)班数学兴趣小组经过市场调查,整理出某商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表
已知该商品的进价为每件30元,设销售该商品每天的 利润为y元.(1)求出y与x的函数表达式;(2)问销售该商品第几天时,当天销售利润最大 最大利润是多少 (3)该商品在销售过程中,共有多少天每天销售利润不低于4800元
请直接写出结果.
巩固提高
时间
每天销量/件
200-2x
售价(元/件)
x+40
1≤x<50
50≤x≤90
时间 x/天
90
九(1)班数学兴趣小组经过市场调查,整理出某商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表
时间
每天销量/件
200-2x
售价(元/件)
x+40
1≤x≤50
50≤x≤90
时间 x/天
90
(1)根据每件利润乘每天销量可得每天利润;
(2)根据分段函数和二次函数、一次函数的性质,
分别得出最值,再比较可得出答案;
(3)根据函数值大于或等于4800可得不等式,
解不等式即可.
分析:
解:(1)当1≤x<50时,
y=(200-2x)(x+40-30)
=-2x2+180x+2000
当50≤x≤90时,
y=(200-2x)(90-30)
=-120x+12000
∴y=
-2x2+180x+2000
-120x+12000
(1≤x<50)
(50≤x≤90)
b
2a
-
且当x= =-
180
2×(-2)
y值最大.
=45时,
y最大值=-2×452+180×45+2000=6050;
∴此二次函数有最大值,
∵一次函数y=-120x+12000的k=-120<0,
(2) 当1≤x<50时,
∵ 二次函数y=-2x2+180x+2000的a=-2<0,
当50≤x≤90时,
∴y随x的增大而减小,
∴当x=50时,y最大值=6000.
综上所述,销售该商品第45天时,当天销售利润最大,最大利润是 6050 元.
(3)当1≤x<50时,
-2x2 +180x+2000≥4800,解得20≤x<30;
当50≤x≤90时,
-120x+12000≥4800,解得 50≤x≤60.
综上所述,当20≤x≤60时,即共有41天每天销售利润不低于4800元.
经验总结:
对于二次函数的应用,先利用“每件利润x每天销量
=每天利润”求函数表达式,再利用函数的性质求最值.
今天作业
课本P58页第11题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
