【精选备课】2022-2023学年沪教版(上海)数学九年级第一学期 24.3三角形一边的平行线 课件(共17张PPT)
文档属性
| 名称 | 【精选备课】2022-2023学年沪教版(上海)数学九年级第一学期 24.3三角形一边的平行线 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 547.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-28 00:00:00 | ||
图片预览

文档简介
(共17张PPT)
24.3三角形一边的平行线
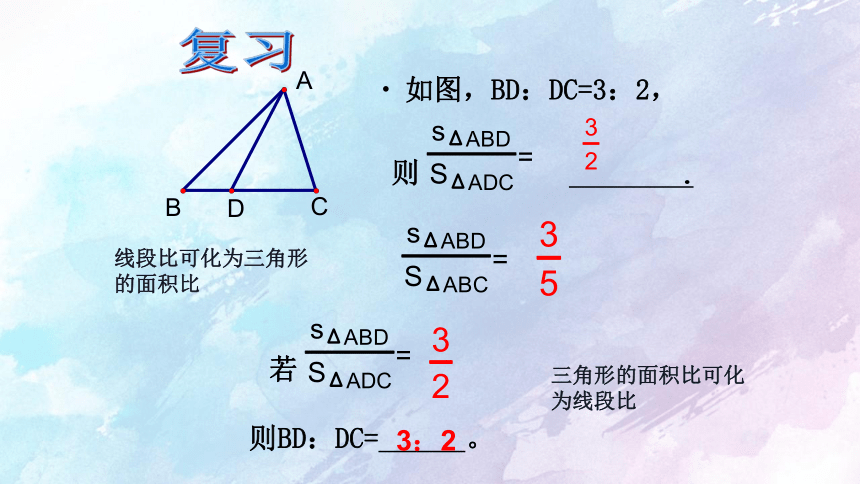
如图,BD:DC=3:2,
则 .
若
则BD:DC= 。
3:2
线段比可化为三角形的面积比
三角形的面积比可化为线段比
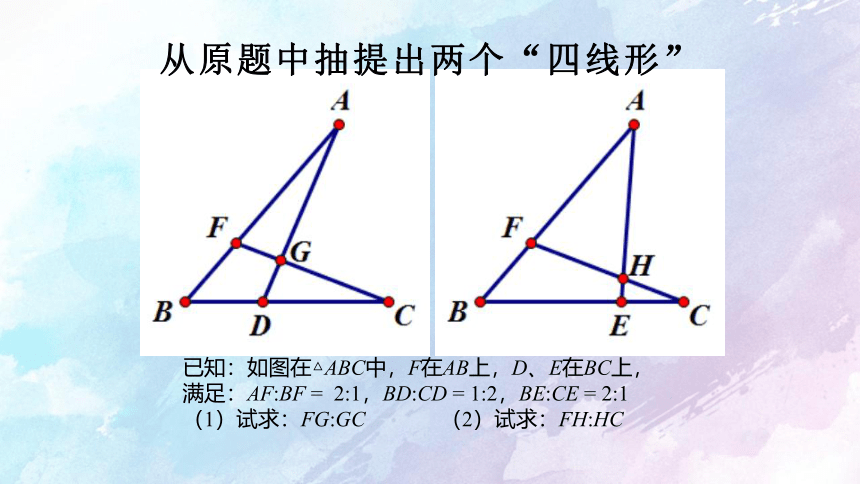
从原题中抽提出两个“四线形”
已知:如图在△ABC中,F在AB上,D、E在BC上,
满足:AF:BF = 2:1,BD:CD = 1:2,BE:CE = 2:1
(1)试求:FG:GC (2)试求:FH:HC
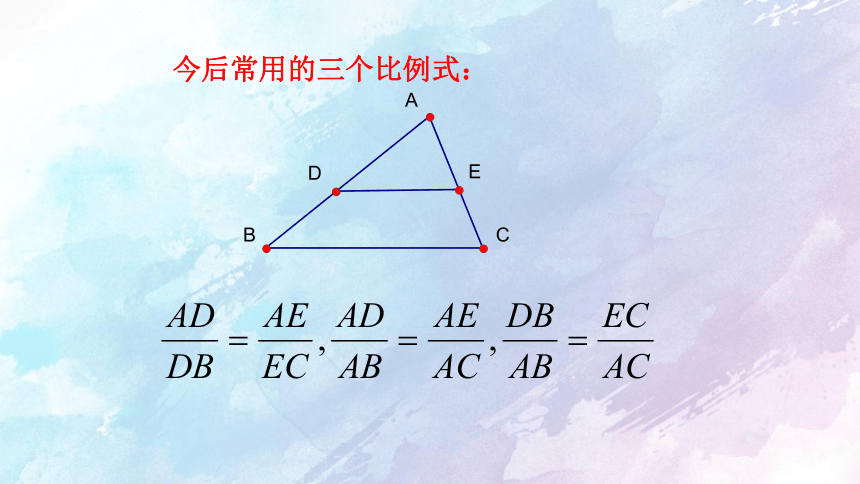
今后常用的三个比例式:
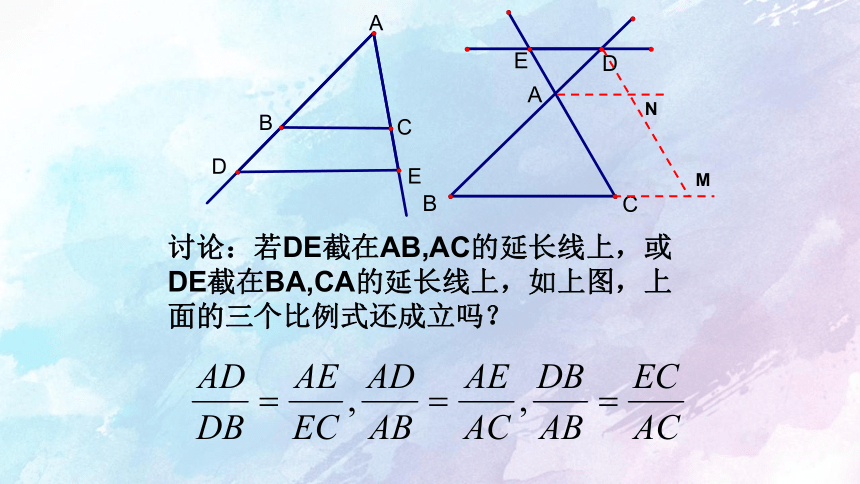
讨论:若DE截在AB,AC的延长线上,或DE截在BA,CA的延长线上,如上图,上面的三个比例式还成立吗?
M
N
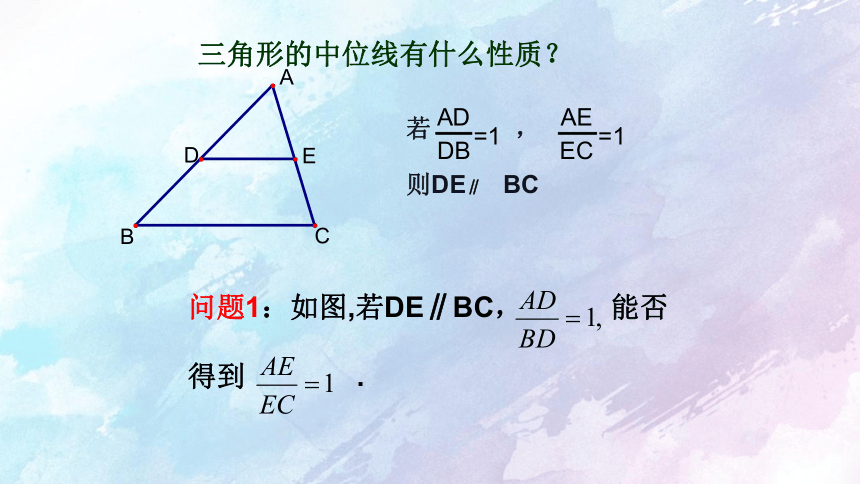
三角形的中位线有什么性质?
若 ,
则DE∥ BC
问题1:如图,若DE∥BC, 能否
得到 .
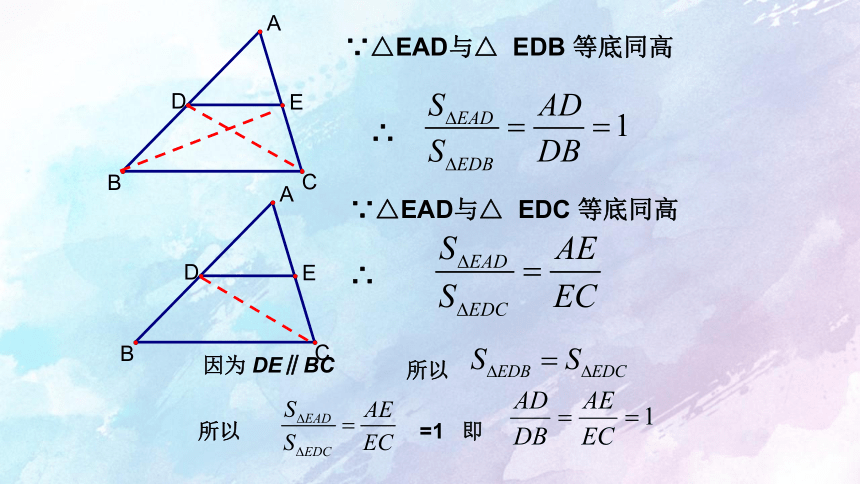
∵△EAD与△ EDB 等底同高
因为 DE∥BC
所以
所以 =1 即
∴
∵△EAD与△ EDC 等底同高
∴
问题2:若将 向下平行移动,
议一议:利用比例的性质,还可以得到哪些成比例线段
D
E
是否仍成立?
,
三角形一边的平行线性质定理:平行于三角形一边的直线截其他两边所在的直线,截得的对应线段成比例.
符号语言:∵DE∥BC
(或
)
强调在同一条线段上的比例关系
例题分析
如图:已知DE∥BC,
AB=15,AC=10,BD=6.
求CE.
解∵DE∥BC,
∴
由AB=15,AC=10,BD=6,得
∴CE=4.
如图BE、CF是△ ABC的中线,交于
点G,求证:
A
B
C
G
E
F
三角形的三条中线交于同一点,这一点叫做三角形的重心
A
B
C
G
●
∵G为 △ABC的重心(已知)
D
∴AD是△ABC的中线
( )
三角形的重心的定义
三角形的重心到一个顶点的距离等于它到这个顶点对边中点的距离的2倍
∵G为 △ABC的重心(已知)
A
B
C
●
G
D
∴AG=2GD
看书P15
检查课本P14练习2
总结
四线形问题的添线规律和解题步骤
首先标记已有条件和所求条件的边
经过这三条边的交点做平行线
构造复合的A型和X型的模型
借助三角形一边平行线的性质定理的推论来解决问题
变式:
1、在ABC中,DE∥BC,
DE与AB相交于D,与AC相交于E.
(1)已知,AD=5,DB=3,AE=4 ,求 EC 的长.
(2)已知,AC=12,EC=4,DB=5 ,则 AB = .
(3)已知,AD:BD=3:2,AC=10则 AE = .
变式:
2、如图,DE∥BC,
DE分别交BA,CA的处长线于E,D
(1)已知,AB=18,AD=5,AE=9 ,则 AC = .
(2)已知,AB=18,CD=15,AE=6则 AC = .
24.3三角形一边的平行线
如图,BD:DC=3:2,
则 .
若
则BD:DC= 。
3:2
线段比可化为三角形的面积比
三角形的面积比可化为线段比
从原题中抽提出两个“四线形”
已知:如图在△ABC中,F在AB上,D、E在BC上,
满足:AF:BF = 2:1,BD:CD = 1:2,BE:CE = 2:1
(1)试求:FG:GC (2)试求:FH:HC
今后常用的三个比例式:
讨论:若DE截在AB,AC的延长线上,或DE截在BA,CA的延长线上,如上图,上面的三个比例式还成立吗?
M
N
三角形的中位线有什么性质?
若 ,
则DE∥ BC
问题1:如图,若DE∥BC, 能否
得到 .
∵△EAD与△ EDB 等底同高
因为 DE∥BC
所以
所以 =1 即
∴
∵△EAD与△ EDC 等底同高
∴
问题2:若将 向下平行移动,
议一议:利用比例的性质,还可以得到哪些成比例线段
D
E
是否仍成立?
,
三角形一边的平行线性质定理:平行于三角形一边的直线截其他两边所在的直线,截得的对应线段成比例.
符号语言:∵DE∥BC
(或
)
强调在同一条线段上的比例关系
例题分析
如图:已知DE∥BC,
AB=15,AC=10,BD=6.
求CE.
解∵DE∥BC,
∴
由AB=15,AC=10,BD=6,得
∴CE=4.
如图BE、CF是△ ABC的中线,交于
点G,求证:
A
B
C
G
E
F
三角形的三条中线交于同一点,这一点叫做三角形的重心
A
B
C
G
●
∵G为 △ABC的重心(已知)
D
∴AD是△ABC的中线
( )
三角形的重心的定义
三角形的重心到一个顶点的距离等于它到这个顶点对边中点的距离的2倍
∵G为 △ABC的重心(已知)
A
B
C
●
G
D
∴AG=2GD
看书P15
检查课本P14练习2
总结
四线形问题的添线规律和解题步骤
首先标记已有条件和所求条件的边
经过这三条边的交点做平行线
构造复合的A型和X型的模型
借助三角形一边平行线的性质定理的推论来解决问题
变式:
1、在ABC中,DE∥BC,
DE与AB相交于D,与AC相交于E.
(1)已知,AD=5,DB=3,AE=4 ,求 EC 的长.
(2)已知,AC=12,EC=4,DB=5 ,则 AB = .
(3)已知,AD:BD=3:2,AC=10则 AE = .
变式:
2、如图,DE∥BC,
DE分别交BA,CA的处长线于E,D
(1)已知,AB=18,AD=5,AE=9 ,则 AC = .
(2)已知,AB=18,CD=15,AE=6则 AC = .
