【精选备课】2022-2023学年沪教版(上海)数学九年级第一学期 25.3解直角三角形 同步练习(含解析)
文档属性
| 名称 | 【精选备课】2022-2023学年沪教版(上海)数学九年级第一学期 25.3解直角三角形 同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-28 00:00:00 | ||
图片预览


文档简介
25.3解直角三角形
一、单选题
1.如图,四边形ABCD中∠DAB=60°,∠B=∠D=90°,BC=1,CD=2,则对角线AC的长为( )
A. B. C. D.
2.如图,电线杆的高度为,两根拉线与相互垂直,,则拉线的长度为(、、在同一条直线上)( )
A. B. C. D.
3.如图,△ABC中,∠A=30°,∠ACB=90°,BC=2,D是AB上的动点,将线段CD绕点C逆时针旋转90°,得到线段CE,连接BE,则BE的最小值是( )
A.-1 B. C. D.2
4.如图,甲、乙为两座建筑物,它们之间的水平距离为,在A点测得D点的仰角为,在B点测得D点的仰角为,则乙建筑物的高度为( )
A. B. C. D.
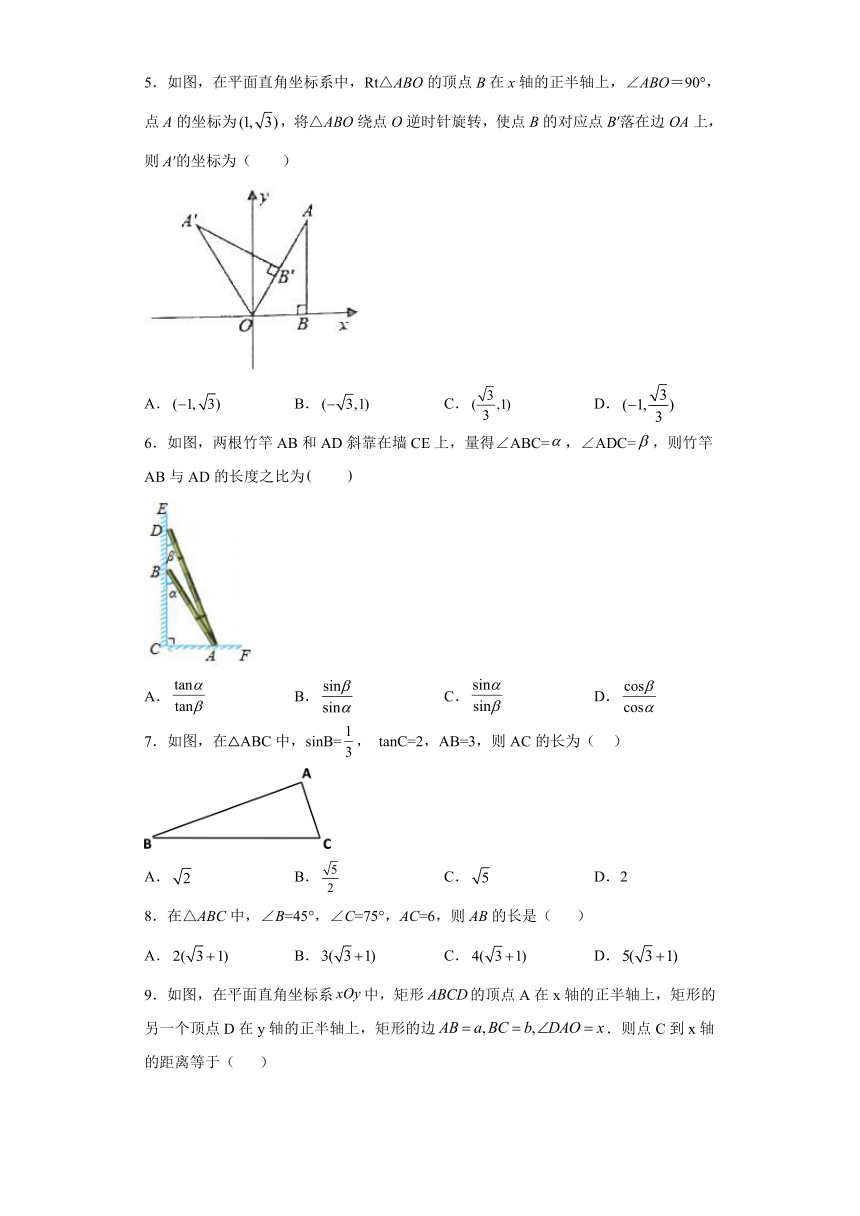
5.如图,在平面直角坐标系中,Rt△ABO的顶点B在x轴的正半轴上,∠ABO=90°,点A的坐标为,将△ABO绕点O逆时针旋转,使点B的对应点B′落在边OA上,则A′的坐标为( )
A. B. C. D.
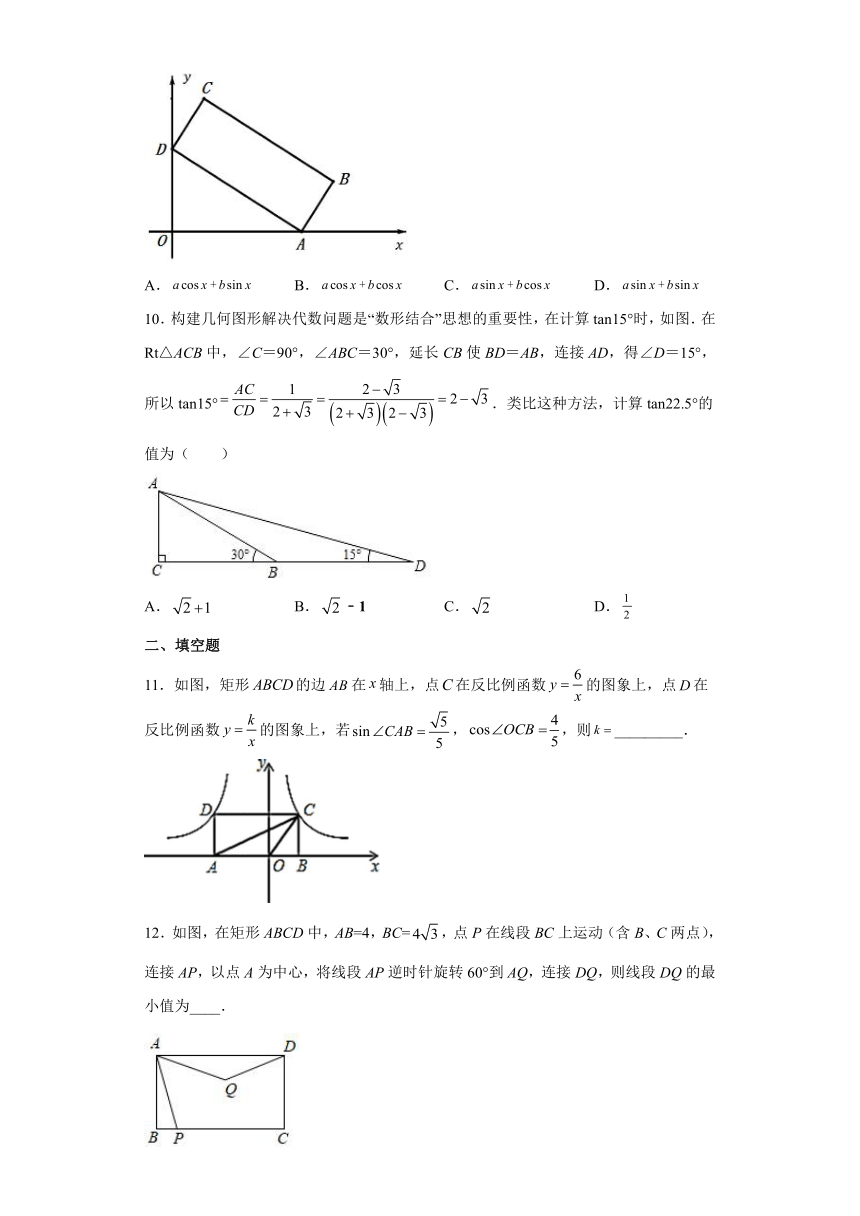
6.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=,∠ADC=,则竹竿AB与AD的长度之比为
A. B. C. D.
7.如图,在△ABC中,sinB=, tanC=2,AB=3,则AC的长为( )
A. B. C. D.2
8.在△ABC中,∠B=45°,∠C=75°,AC=6,则AB的长是( )
A. B. C. D.
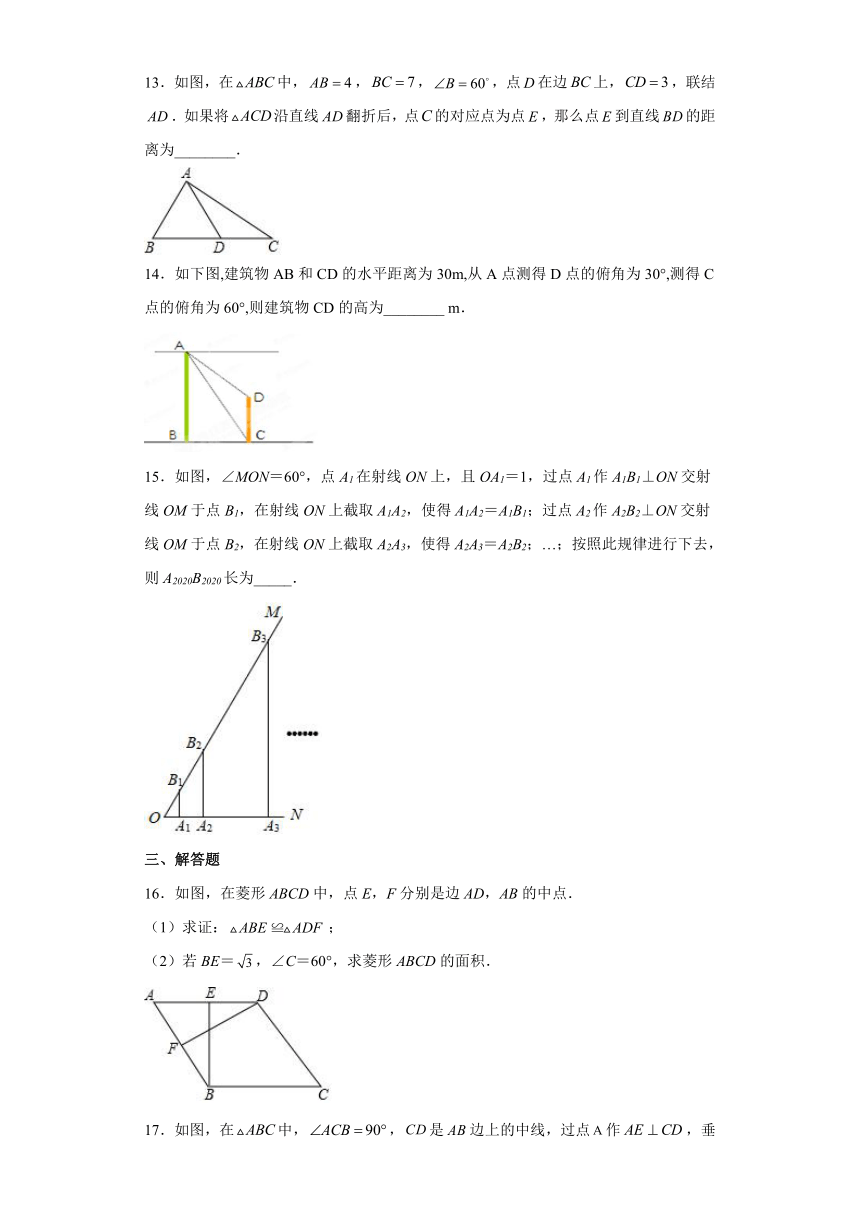
9.如图,在平面直角坐标系中,矩形的顶点A在x轴的正半轴上,矩形的另一个顶点D在y轴的正半轴上,矩形的边.则点C到x轴的距离等于( )
A. B. C. D.
10.构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°.类比这种方法,计算tan22.5°的值为( )
A. B.﹣1 C. D.
二、填空题
11.如图,矩形的边在轴上,点在反比例函数的图象上,点在反比例函数的图象上,若,,则_________.
12.如图,在矩形ABCD中,AB=4,BC=,点P在线段BC上运动(含B、C两点),连接AP,以点A为中心,将线段AP逆时针旋转60°到AQ,连接DQ,则线段DQ的最小值为____.
13.如图,在中,,,,点在边上,,联结.如果将沿直线翻折后,点的对应点为点,那么点到直线的距离为________.
14.如下图,建筑物AB和CD的水平距离为30m,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为________ m.
15.如图,∠MON=60°,点A1在射线ON上,且OA1=1,过点A1作A1B1⊥ON交射线OM于点B1,在射线ON上截取A1A2,使得A1A2=A1B1;过点A2作A2B2⊥ON交射线OM于点B2,在射线ON上截取A2A3,使得A2A3=A2B2;…;按照此规律进行下去,则A2020B2020长为_____.
三、解答题
16.如图,在菱形ABCD中,点E,F分别是边AD,AB的中点.
(1)求证:;
(2)若BE=,∠C=60°,求菱形ABCD的面积.
17.如图,在中,,是边上的中线,过点作,垂足为,交于点,.
(1)求的值:
(2)若,求的长.
18.如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,求∠A的正弦值、余弦值和正切值.
19.如图,两楼地面距离BC为米,楼AB高30米,从楼AB的顶部点A测得楼CD顶部点D的仰角为45度.
(1)求的大小;
(2)求楼CD的高度(结果保留根号).
20.如图,矩形在平面直角坐标系中, 交 轴于点,动点 从原点出发,以每秒 1 个单位长度的速度沿 轴正方向移动,移动时间为秒,过点 P 作垂直于 轴的直线,交 于点 M ,交 或 于点 N ,直线扫过矩形 的面积为.
(1)求点 的坐标;
(2)求直线 移动过程中到点之前的 关于 的函数关系式;
(3)在直线 移动过程中,第一象限的直线上是否存在一点 ,使 是等腰直角三角形 若存在,直接写出点 的坐标;若不存在,说明理由
参考答案:
1.C
【解析】
【分析】
延长DC与AB交于一点K.解直角三角形求出DK,再求出AD,再在△Rt△ADC中利用勾股定理求出AC.
【详解】
解:延长DC交AB的延长线于点K;
在Rt△ADK中,∠DAK=60°∠AKD=30°,BC=1,
∴CK=2,BK=,
∴DK=CD+CK=4,
∴AD==
在△Rt△ADC中,
AC==
故选C.
【点睛】
考查了解直角三角形的应用,解题关键在于构造RtADK,然后再解直角三角形即可.
2.B
【解析】
【分析】
先通过等量代换得出,然后利用余弦的定义即可得出结论.
【详解】
故选:B.
【点睛】
本题主要考查解直角三角形,掌握余弦的定义是解题的关键.
3.A
【解析】
【分析】
过点C作CK⊥AB于点K,将线段CK绕点C逆时针旋转90° 得到CH,连接HE,延长HE交AB的延长线于点J;通过证明△CKD≌△CHE (ASA),进而证明所构建的四边形CKJH是正方形,所以当点E与点J重合时,BE的值最小,再通过在Rt△CBK中已知的边角条件,即可求出答案.
【详解】
解:如图,过点C作CK⊥AB于点K,将线段CK绕点C逆时针旋转90° 得到CH,连接HE,延长HE交AB的延长线于点J
∵将线段CD绕点C逆时针旋转90° ,得到线段CE
∴∠DCE=∠KCH = 90°
∵∠ECH=∠KCH - ∠KCE,∠DCK =∠DCE-∠KCE
∴∠ECH =∠DCK
又∵CD= CE,CK = CH
∴在△CKD和△CHE中
∴△CKD≌△CHE (ASA)
∴∠CKD=∠H=90°,CH=CK
∴∠CKJ =∠KCH =∠H=90°
∴四边形CKJH是正方形
∴CH=HJ=KJ=C'K
∴点E在直线HJ上运动,当点E与点J重合时,BE的值最小
∵∠A= 30°
∴∠ABC=60°
在Rt△CBK中,BC= 2
∴CK = BCsin60°=,BK=BCcos60° = 1
∴KJ = CK =
所以BJ = KJ-BK=
BE的最小值为
故选A.
【点睛】
本题主要考查了以线段旋转为载体的求线段最短问题,正方形的构建是快速解答本题的关键.
4.B
【解析】
【分析】
在中,解直角三角形,可求得CD的长,即求得甲的高度,过A作AF⊥CD于点F,在中解直角三角形可求得DF,则可求得CF的长,即可求得乙的高度.
【详解】
如图,过点A作于点F,在中,
,,
∴,
在中,,
∴,
∴,
即乙建筑物的高度为.
故答案选:B.
【点睛】
本题主要考查解直角三角形的应用-仰角俯角问题,构造直角三角形,利用特殊角求得相应线段的长是解题的关键.
5.A
【解析】
【分析】
过点作C⊥x轴于C,勾股定理求出OA,根据正切公式求出,由此得到∠OC=60°,根据三角函数求出OC,C,即可得到的坐标.
【详解】
解:过点作C⊥x轴于C,
∵点A的坐标为,∠ABO=90°,
∴,
∴
∴
∴,
由旋转的性质可得,
∴∠OC=60°,
∴OC=Ocos60°=1,C=Osin60°=,
∴(-1,),
故选:A.
.
【点睛】
此题考查了旋转的性质,勾股定理,三角函数,求坐标系中点的坐标的方法:从该点向坐标轴作垂线,求对应线段的长度即可.
6.B
【解析】
【分析】
在两个直角三角形中,分别求出AB、AD即可解决问题;
【详解】
在Rt△ABC中,AB=,
在Rt△ACD中,AD=,
∴AB:AD=:=,
故选B.
【点睛】
本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是学会利用参数解决问题.
7.B
【解析】
【分析】
过A点作AH⊥BC于H点,先由sin∠B及AB=3算出AH的长,再由tan∠C算出CH的长,最后在Rt△ACH中由勾股定理即可算出AC的长.
【详解】
解:过A点作AH⊥BC于H点,如下图所示:
由,且可知,,
由,且可知,,
∴在中,由勾股定理有:.
故选:B.
【点睛】
本题考查了解直角三角形及勾股定理等知识,如果图形中无直角三角形时,可以通过作垂线构造直角三角形进而求解.
8.B
【解析】
【分析】
作CD⊥AB于D,则△BCD是等腰直角三角形,得BD=CD,∠BCD=45°,求出∠ACD=30°,由直角三角形的性质得AD=AC=3,BD=CD=AD=3,即可得出答案.
【详解】
解:作CD⊥AB于D,如图所示:
则∠BDC=∠ADC=90°,
∵∠B=45°,
∴△BCD是等腰直角三角形,
∴BD=CD,∠BCD=45°,
∵∠ACB=75°,
∴∠ACD=∠ACB-∠BCD=30°,
∴AD=AC=×6=3,CD= =3,
∴BD=CD=3,
∴AB=BD+AD=3+3=3(+1);
故选:B.
【点睛】
本题考查了解直角三角形、等腰直角三角形的判定与性质、含30°角的直角三角形的性质等知识;正确作出辅助线构造直角三角形是解题的关键.
9.A
【解析】
【分析】
作CE⊥y轴于E.解直角三角形求出OD,DE即可解决问题.
【详解】
作CE⊥y轴于E.
在Rt△OAD中,
∵∠AOD=90°,AD=BC=,∠OAD=,
∴OD=,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴∠CDE+∠ADO=90°,
又∵∠OAD+∠ADO=90°,
∴∠CDE=∠OAD=,
∴在Rt△CDE中,
∵CD=AB=,∠CDE=,
∴DE=,
∴点C到轴的距离=EO=DE+OD=,
故选:A.
【点睛】
本题考查了解直角三角形的应用,矩形的性质,正确作出辅助线是解题的关键.
10.B
【解析】
【分析】
作Rt△ABC,使∠C=90°,∠ABC=45°,延长CB到D,使BD=AB,连接AD,根据构造的直角三角形,设AC=x,再用x表示出CD,即可求出tan22.5°的值.
【详解】
解:作Rt△ABC,使∠C=90°,∠ABC=90°,∠ABC=45°,延长CB到D,使BD=AB,连接AD,设AC=x,则:BC=x,AB=,CD=,
故选:B.
【点睛】
本题考查解直角三角形,解题的关键是根据阅读构造含45°的直角三角形,再作辅助线得到22.5°的直角三角形.
11.-10
【解析】
【分析】
设C(x,),根据求出OB,BC,再根据求出AC,由勾股定理求出AB,从而得出AO,得到D的坐标,进而求出k的值.
【详解】
解:设C(x,)(x>0),
,,
∵四边形ABCD是矩形,
,,
,
,
,即,
解得,,(舍去),
,,
,
,即,
,
,
,
,
∵D在函数的图象上,
.
故答案为:-10.
【点睛】
此题是一道综合性较强的题目,将解直角三角形和用待定系数法求函数解析式结合起来,有一定难度.
12.2
【解析】
【分析】
以AB为边向右作等边,作射线FQ交AD于点E,过点D作DH⊥QE于点H,证明△BAP △FAQ,由全等性质可以得到∠ABP=∠AFQ,进一步解三角形求得AE的值,判断出点Q的运动轨迹是射线FE,在△DHE中,当点Q与点H重合时,DH的值最小,利用特殊角的锐角三角函数值求解即可.
【详解】
解:以AB为边向右作等边,作射线FQ交AD于点E,过点D作DH⊥QE于点H,如下图:
∵四边形ABCD是矩形
∴∠ABP=∠BAE=
∵△ABF和△APQ是等边三角形
∴∠BAF=∠PAQ=,BA=FA,PA=QA
∴∠BAP+∠PAF=∠PAF+∠FAQ
∴∠BAP=∠FAQ
在△BAP和△FAQ中,
∴
∴∠ABP=∠AFQ=
∵∠FAE=
∴∠AEF=
∵AB=AF=4
∴
∴点Q的运动轨迹是射线FE
∵AD=BC=
∴DE=AD-AE=
∵DH⊥EF,∠DEH=∠AEF=
∴
由垂线段最短可知,当点Q与点H重合时,DH的值最小,最小值为
故答案为:2
【点睛】
本题考查三角形全等的性质和证明,等边三角形的性质,特殊角的三角函数值计算等相关知识点,能够根据已知条件作出相关的辅助线是解题重点.
13.
【解析】
【分析】
如图,过点 E作 EH⊥BC于H.首先证明 是等边三角形,解直角三角形求出 即可
【详解】
解:如图,过点作于.
∵ ,,
∴ .
∵ ,,
∴ 是等边三角形,
∴ ,
∴ ,
∴ .
∵ ,
∴ .
∵ ,
∴ ,
∴ 到直线的距离为.
【点睛】
本题考查三角形翻折问题和等边三角形性质、有角为60°直角三角形性质运用,掌握这些知识点是解题关键.
14.20m
【解析】
【分析】
延长CD交AM于点E.在Rt△ACE中,可求出CE;在Rt△ADE中,可求出DE.CD=CE-DE.
【详解】
解:延长CD交AM于点E,则AE=30.
∴
同理可得
∴(米)
故答案为
【点睛】
考查利用解直角三角形知识解决实际问题的能力.
15.(1+)2019
【解析】
【分析】
解直角三角形求出A1B1,A2B2,A3B3,…,探究规律利用规律即可解决问题.
【详解】
解:在Rt△OA1B1中,
∵∠OA1B1=90°,∠MON=60°,OA1=1,
∴A1B1=A1A2=OA1 tan60°=,
∵A1B1∥A2B2,
∴,
∴,
∴A2B2=(1+),
同法可得,A3B3=(1+)2,
……
由此规律可知,A2020B2020=(1+)2019,
故答案为:(1+)2019.
【点睛】
本题考查解直角三角形,规律型问题,解题的关键是学会探究规律的方法,属于中考常考题型.
16.(1)详见解析;(2)2.
【解析】
【分析】
(1)利用菱形的性质,由SAS证明即可;
(2)证是等边三角形,得出BE⊥AD,求出AD即可.
【详解】
(1)证明:∵四边形ABCD是菱形,
∴AB=AD,
∵点E,F分别是边AD,AB的中点,
∴AF=AE,
在和中,
,
∴(SAS);
(2)解:连接BD,如图:
∵四边形ABCD是菱形,
∴AB=AD,∠A=∠C=60°,
∴是等边三角形,
∵点E是边AD的中点,
∴BE⊥AD,
∴∠ABE=30°,
∴AE=BE=1,AB=2AE=2,
∴AD=AB=2,
∴菱形ABCD的面积=AD×BE=2×=2.
【点睛】
本题考查的是菱形的性质,等边三角形的判定与性质,菱形的面积的计算,掌握以上知识是解题的关键.
17.(1);(2)4
【解析】
【分析】
(1)根据∠ACB=90°,CD是斜边AB上的中线,可得出CD=BD,则∠B=∠BCD,再由AE⊥CD,可证明∠B=∠CAM,由AM=2CM,可得出CM:AC=1:,即可得出sinB的值;
(2)根据sinB的值,可得出AC:AB=1:,再由AB=,得AC=2,根据勾股定理即可得出结论.
【详解】
(1)∵,是斜边的中线,
∴,
∴,
∵,
∴.
∵,
∴.
∴.
在中,∵,
∴.
∴.
(2)∵,
∴.
由(1)知,
∴.
∴.
【点睛】
本题主要考查了勾股定理和锐角三角比,熟练掌握根据锐角三角比解直角三角形是解题的关键.
18.sinA=,cosA=,tanA=.
【解析】
【分析】
根据勾股定理求出AB,根据锐角三角函数的定义解答即可.
【详解】
由勾股定理得,,
则,,.
【点睛】
本题考查解直角三角形,解题的关键是利用勾股定理求出AB的长.
19.(1)75°;(2)
【解析】
【分析】
(1)如图:过点A作于点E,在Rt△ABC中运用三角函数可得,即、进一步可得∠EAC=30°,再结合即可解答;
(2)先根据题意求得DE=AE=,然后在Rt△ACE中解直角三角形求得CE,最后利用CD=CE+DE进行计算即可.
【详解】
(1)如图:过点A作于点E,
∵在Rt△ABC中,
∵AE//BC
;
(2)∵在RtAED中,AE=BC=,∠DAE=45°
∴DE=AE=
∵在Rt△ACE中,∠CAE=30°
∴CE=tan30°·AE=30
.
【点睛】
本题主要考查了运用三角函数值求角的大小和解直角三角形,灵活应用三角函数知识是解答本题的关键.
20.(1);(2);(3)存在.
【解析】
【分析】
(1)由 ,且AB=6即可求出AO的长,再由勾股定理即可求出BO的长,即可求出A和B点坐标.
(2)P点从原点出发,在到达终点前,直线l扫过的面积始终为平行四边形BMNE,故求该平行四边的底BE和高OP,相乘即得到面积S;由,且AB=6,可求出AC=10,过D点作DF⊥x轴,易证,求出CF=AO,进而求出OF的长;由,故,求出OE的长,进而求出OB+OE=BE.
(3)分类讨论,当B为直角顶角时,过Q1点作QH⊥y轴,此时△Q1HB≌△BOC,即可求出Q1的坐标;当Q2为直角顶角时,过Q2点作QM⊥y轴,QN⊥x轴,此时Q2MB≌Q2NC,即可求出Q2的坐标.
【详解】
解:(1)由题意可得
故答案为:
(2)过点作轴,垂足为 F ,则
∴
∵
∴,故,求得
.
当时,直线 扫过的图形是平行四边形,
故答案为:.
存在,.如下图所示:
情况一:当B为直角顶角时,此时BQ1=BC,过Q1点作Q1H1⊥y轴于H1,
∴∠Q1H1B=∠BOC=90°,且BQ1=BC,
∵∠Q1BC=90°
∴∠H1BQ1+∠OBC=90°
又∠BCO+∠OBC=90°
∴∠H1BO1=∠BCO
在△Q1H1B和△BOC中:
,∴△△Q1H1B≌△BOC(AAS)
∴Q1H1=BO=,BH1=OC=,∴OH1=
∴
情况二:当Q2为直角顶角时,此时有Q2B=Q2C,
过Q2点分别作Q2M⊥y轴,Q2N⊥x轴
∴∠MQ2B+∠BQ2N=90°
又∴∠NQ2C+∠BQ2N=90°
∴∠MQ2B =∠NQ2C
在△MQ2B和△NQ2C中
,∴△MQ2B≌△NQ2C(AAS)
∴MQ2= NQ2=OM=ON,且∠MON=90°
∴四边形Q2MON为正方形,设MB=NC=a
则OC-a=ON=OB=,且OC=
∴求得a=,∴ON=OM=OB+a=
∴
故答案为:和
【点睛】
本题考查了三角函数求值、平行四边形的面积公式、三角形全等、等腰直角三角形等相关知识,利用锐角相等,其对应的三角函数值相同,可列出比例求解未知线段长.
一、单选题
1.如图,四边形ABCD中∠DAB=60°,∠B=∠D=90°,BC=1,CD=2,则对角线AC的长为( )
A. B. C. D.
2.如图,电线杆的高度为,两根拉线与相互垂直,,则拉线的长度为(、、在同一条直线上)( )
A. B. C. D.
3.如图,△ABC中,∠A=30°,∠ACB=90°,BC=2,D是AB上的动点,将线段CD绕点C逆时针旋转90°,得到线段CE,连接BE,则BE的最小值是( )
A.-1 B. C. D.2
4.如图,甲、乙为两座建筑物,它们之间的水平距离为,在A点测得D点的仰角为,在B点测得D点的仰角为,则乙建筑物的高度为( )
A. B. C. D.
5.如图,在平面直角坐标系中,Rt△ABO的顶点B在x轴的正半轴上,∠ABO=90°,点A的坐标为,将△ABO绕点O逆时针旋转,使点B的对应点B′落在边OA上,则A′的坐标为( )
A. B. C. D.
6.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=,∠ADC=,则竹竿AB与AD的长度之比为
A. B. C. D.
7.如图,在△ABC中,sinB=, tanC=2,AB=3,则AC的长为( )
A. B. C. D.2
8.在△ABC中,∠B=45°,∠C=75°,AC=6,则AB的长是( )
A. B. C. D.
9.如图,在平面直角坐标系中,矩形的顶点A在x轴的正半轴上,矩形的另一个顶点D在y轴的正半轴上,矩形的边.则点C到x轴的距离等于( )
A. B. C. D.
10.构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°.类比这种方法,计算tan22.5°的值为( )
A. B.﹣1 C. D.
二、填空题
11.如图,矩形的边在轴上,点在反比例函数的图象上,点在反比例函数的图象上,若,,则_________.
12.如图,在矩形ABCD中,AB=4,BC=,点P在线段BC上运动(含B、C两点),连接AP,以点A为中心,将线段AP逆时针旋转60°到AQ,连接DQ,则线段DQ的最小值为____.
13.如图,在中,,,,点在边上,,联结.如果将沿直线翻折后,点的对应点为点,那么点到直线的距离为________.
14.如下图,建筑物AB和CD的水平距离为30m,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为________ m.
15.如图,∠MON=60°,点A1在射线ON上,且OA1=1,过点A1作A1B1⊥ON交射线OM于点B1,在射线ON上截取A1A2,使得A1A2=A1B1;过点A2作A2B2⊥ON交射线OM于点B2,在射线ON上截取A2A3,使得A2A3=A2B2;…;按照此规律进行下去,则A2020B2020长为_____.
三、解答题
16.如图,在菱形ABCD中,点E,F分别是边AD,AB的中点.
(1)求证:;
(2)若BE=,∠C=60°,求菱形ABCD的面积.
17.如图,在中,,是边上的中线,过点作,垂足为,交于点,.
(1)求的值:
(2)若,求的长.
18.如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,求∠A的正弦值、余弦值和正切值.
19.如图,两楼地面距离BC为米,楼AB高30米,从楼AB的顶部点A测得楼CD顶部点D的仰角为45度.
(1)求的大小;
(2)求楼CD的高度(结果保留根号).
20.如图,矩形在平面直角坐标系中, 交 轴于点,动点 从原点出发,以每秒 1 个单位长度的速度沿 轴正方向移动,移动时间为秒,过点 P 作垂直于 轴的直线,交 于点 M ,交 或 于点 N ,直线扫过矩形 的面积为.
(1)求点 的坐标;
(2)求直线 移动过程中到点之前的 关于 的函数关系式;
(3)在直线 移动过程中,第一象限的直线上是否存在一点 ,使 是等腰直角三角形 若存在,直接写出点 的坐标;若不存在,说明理由
参考答案:
1.C
【解析】
【分析】
延长DC与AB交于一点K.解直角三角形求出DK,再求出AD,再在△Rt△ADC中利用勾股定理求出AC.
【详解】
解:延长DC交AB的延长线于点K;
在Rt△ADK中,∠DAK=60°∠AKD=30°,BC=1,
∴CK=2,BK=,
∴DK=CD+CK=4,
∴AD==
在△Rt△ADC中,
AC==
故选C.
【点睛】
考查了解直角三角形的应用,解题关键在于构造RtADK,然后再解直角三角形即可.
2.B
【解析】
【分析】
先通过等量代换得出,然后利用余弦的定义即可得出结论.
【详解】
故选:B.
【点睛】
本题主要考查解直角三角形,掌握余弦的定义是解题的关键.
3.A
【解析】
【分析】
过点C作CK⊥AB于点K,将线段CK绕点C逆时针旋转90° 得到CH,连接HE,延长HE交AB的延长线于点J;通过证明△CKD≌△CHE (ASA),进而证明所构建的四边形CKJH是正方形,所以当点E与点J重合时,BE的值最小,再通过在Rt△CBK中已知的边角条件,即可求出答案.
【详解】
解:如图,过点C作CK⊥AB于点K,将线段CK绕点C逆时针旋转90° 得到CH,连接HE,延长HE交AB的延长线于点J
∵将线段CD绕点C逆时针旋转90° ,得到线段CE
∴∠DCE=∠KCH = 90°
∵∠ECH=∠KCH - ∠KCE,∠DCK =∠DCE-∠KCE
∴∠ECH =∠DCK
又∵CD= CE,CK = CH
∴在△CKD和△CHE中
∴△CKD≌△CHE (ASA)
∴∠CKD=∠H=90°,CH=CK
∴∠CKJ =∠KCH =∠H=90°
∴四边形CKJH是正方形
∴CH=HJ=KJ=C'K
∴点E在直线HJ上运动,当点E与点J重合时,BE的值最小
∵∠A= 30°
∴∠ABC=60°
在Rt△CBK中,BC= 2
∴CK = BCsin60°=,BK=BCcos60° = 1
∴KJ = CK =
所以BJ = KJ-BK=
BE的最小值为
故选A.
【点睛】
本题主要考查了以线段旋转为载体的求线段最短问题,正方形的构建是快速解答本题的关键.
4.B
【解析】
【分析】
在中,解直角三角形,可求得CD的长,即求得甲的高度,过A作AF⊥CD于点F,在中解直角三角形可求得DF,则可求得CF的长,即可求得乙的高度.
【详解】
如图,过点A作于点F,在中,
,,
∴,
在中,,
∴,
∴,
即乙建筑物的高度为.
故答案选:B.
【点睛】
本题主要考查解直角三角形的应用-仰角俯角问题,构造直角三角形,利用特殊角求得相应线段的长是解题的关键.
5.A
【解析】
【分析】
过点作C⊥x轴于C,勾股定理求出OA,根据正切公式求出,由此得到∠OC=60°,根据三角函数求出OC,C,即可得到的坐标.
【详解】
解:过点作C⊥x轴于C,
∵点A的坐标为,∠ABO=90°,
∴,
∴
∴
∴,
由旋转的性质可得,
∴∠OC=60°,
∴OC=Ocos60°=1,C=Osin60°=,
∴(-1,),
故选:A.
.
【点睛】
此题考查了旋转的性质,勾股定理,三角函数,求坐标系中点的坐标的方法:从该点向坐标轴作垂线,求对应线段的长度即可.
6.B
【解析】
【分析】
在两个直角三角形中,分别求出AB、AD即可解决问题;
【详解】
在Rt△ABC中,AB=,
在Rt△ACD中,AD=,
∴AB:AD=:=,
故选B.
【点睛】
本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是学会利用参数解决问题.
7.B
【解析】
【分析】
过A点作AH⊥BC于H点,先由sin∠B及AB=3算出AH的长,再由tan∠C算出CH的长,最后在Rt△ACH中由勾股定理即可算出AC的长.
【详解】
解:过A点作AH⊥BC于H点,如下图所示:
由,且可知,,
由,且可知,,
∴在中,由勾股定理有:.
故选:B.
【点睛】
本题考查了解直角三角形及勾股定理等知识,如果图形中无直角三角形时,可以通过作垂线构造直角三角形进而求解.
8.B
【解析】
【分析】
作CD⊥AB于D,则△BCD是等腰直角三角形,得BD=CD,∠BCD=45°,求出∠ACD=30°,由直角三角形的性质得AD=AC=3,BD=CD=AD=3,即可得出答案.
【详解】
解:作CD⊥AB于D,如图所示:
则∠BDC=∠ADC=90°,
∵∠B=45°,
∴△BCD是等腰直角三角形,
∴BD=CD,∠BCD=45°,
∵∠ACB=75°,
∴∠ACD=∠ACB-∠BCD=30°,
∴AD=AC=×6=3,CD= =3,
∴BD=CD=3,
∴AB=BD+AD=3+3=3(+1);
故选:B.
【点睛】
本题考查了解直角三角形、等腰直角三角形的判定与性质、含30°角的直角三角形的性质等知识;正确作出辅助线构造直角三角形是解题的关键.
9.A
【解析】
【分析】
作CE⊥y轴于E.解直角三角形求出OD,DE即可解决问题.
【详解】
作CE⊥y轴于E.
在Rt△OAD中,
∵∠AOD=90°,AD=BC=,∠OAD=,
∴OD=,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴∠CDE+∠ADO=90°,
又∵∠OAD+∠ADO=90°,
∴∠CDE=∠OAD=,
∴在Rt△CDE中,
∵CD=AB=,∠CDE=,
∴DE=,
∴点C到轴的距离=EO=DE+OD=,
故选:A.
【点睛】
本题考查了解直角三角形的应用,矩形的性质,正确作出辅助线是解题的关键.
10.B
【解析】
【分析】
作Rt△ABC,使∠C=90°,∠ABC=45°,延长CB到D,使BD=AB,连接AD,根据构造的直角三角形,设AC=x,再用x表示出CD,即可求出tan22.5°的值.
【详解】
解:作Rt△ABC,使∠C=90°,∠ABC=90°,∠ABC=45°,延长CB到D,使BD=AB,连接AD,设AC=x,则:BC=x,AB=,CD=,
故选:B.
【点睛】
本题考查解直角三角形,解题的关键是根据阅读构造含45°的直角三角形,再作辅助线得到22.5°的直角三角形.
11.-10
【解析】
【分析】
设C(x,),根据求出OB,BC,再根据求出AC,由勾股定理求出AB,从而得出AO,得到D的坐标,进而求出k的值.
【详解】
解:设C(x,)(x>0),
,,
∵四边形ABCD是矩形,
,,
,
,
,即,
解得,,(舍去),
,,
,
,即,
,
,
,
,
∵D在函数的图象上,
.
故答案为:-10.
【点睛】
此题是一道综合性较强的题目,将解直角三角形和用待定系数法求函数解析式结合起来,有一定难度.
12.2
【解析】
【分析】
以AB为边向右作等边,作射线FQ交AD于点E,过点D作DH⊥QE于点H,证明△BAP △FAQ,由全等性质可以得到∠ABP=∠AFQ,进一步解三角形求得AE的值,判断出点Q的运动轨迹是射线FE,在△DHE中,当点Q与点H重合时,DH的值最小,利用特殊角的锐角三角函数值求解即可.
【详解】
解:以AB为边向右作等边,作射线FQ交AD于点E,过点D作DH⊥QE于点H,如下图:
∵四边形ABCD是矩形
∴∠ABP=∠BAE=
∵△ABF和△APQ是等边三角形
∴∠BAF=∠PAQ=,BA=FA,PA=QA
∴∠BAP+∠PAF=∠PAF+∠FAQ
∴∠BAP=∠FAQ
在△BAP和△FAQ中,
∴
∴∠ABP=∠AFQ=
∵∠FAE=
∴∠AEF=
∵AB=AF=4
∴
∴点Q的运动轨迹是射线FE
∵AD=BC=
∴DE=AD-AE=
∵DH⊥EF,∠DEH=∠AEF=
∴
由垂线段最短可知,当点Q与点H重合时,DH的值最小,最小值为
故答案为:2
【点睛】
本题考查三角形全等的性质和证明,等边三角形的性质,特殊角的三角函数值计算等相关知识点,能够根据已知条件作出相关的辅助线是解题重点.
13.
【解析】
【分析】
如图,过点 E作 EH⊥BC于H.首先证明 是等边三角形,解直角三角形求出 即可
【详解】
解:如图,过点作于.
∵ ,,
∴ .
∵ ,,
∴ 是等边三角形,
∴ ,
∴ ,
∴ .
∵ ,
∴ .
∵ ,
∴ ,
∴ 到直线的距离为.
【点睛】
本题考查三角形翻折问题和等边三角形性质、有角为60°直角三角形性质运用,掌握这些知识点是解题关键.
14.20m
【解析】
【分析】
延长CD交AM于点E.在Rt△ACE中,可求出CE;在Rt△ADE中,可求出DE.CD=CE-DE.
【详解】
解:延长CD交AM于点E,则AE=30.
∴
同理可得
∴(米)
故答案为
【点睛】
考查利用解直角三角形知识解决实际问题的能力.
15.(1+)2019
【解析】
【分析】
解直角三角形求出A1B1,A2B2,A3B3,…,探究规律利用规律即可解决问题.
【详解】
解:在Rt△OA1B1中,
∵∠OA1B1=90°,∠MON=60°,OA1=1,
∴A1B1=A1A2=OA1 tan60°=,
∵A1B1∥A2B2,
∴,
∴,
∴A2B2=(1+),
同法可得,A3B3=(1+)2,
……
由此规律可知,A2020B2020=(1+)2019,
故答案为:(1+)2019.
【点睛】
本题考查解直角三角形,规律型问题,解题的关键是学会探究规律的方法,属于中考常考题型.
16.(1)详见解析;(2)2.
【解析】
【分析】
(1)利用菱形的性质,由SAS证明即可;
(2)证是等边三角形,得出BE⊥AD,求出AD即可.
【详解】
(1)证明:∵四边形ABCD是菱形,
∴AB=AD,
∵点E,F分别是边AD,AB的中点,
∴AF=AE,
在和中,
,
∴(SAS);
(2)解:连接BD,如图:
∵四边形ABCD是菱形,
∴AB=AD,∠A=∠C=60°,
∴是等边三角形,
∵点E是边AD的中点,
∴BE⊥AD,
∴∠ABE=30°,
∴AE=BE=1,AB=2AE=2,
∴AD=AB=2,
∴菱形ABCD的面积=AD×BE=2×=2.
【点睛】
本题考查的是菱形的性质,等边三角形的判定与性质,菱形的面积的计算,掌握以上知识是解题的关键.
17.(1);(2)4
【解析】
【分析】
(1)根据∠ACB=90°,CD是斜边AB上的中线,可得出CD=BD,则∠B=∠BCD,再由AE⊥CD,可证明∠B=∠CAM,由AM=2CM,可得出CM:AC=1:,即可得出sinB的值;
(2)根据sinB的值,可得出AC:AB=1:,再由AB=,得AC=2,根据勾股定理即可得出结论.
【详解】
(1)∵,是斜边的中线,
∴,
∴,
∵,
∴.
∵,
∴.
∴.
在中,∵,
∴.
∴.
(2)∵,
∴.
由(1)知,
∴.
∴.
【点睛】
本题主要考查了勾股定理和锐角三角比,熟练掌握根据锐角三角比解直角三角形是解题的关键.
18.sinA=,cosA=,tanA=.
【解析】
【分析】
根据勾股定理求出AB,根据锐角三角函数的定义解答即可.
【详解】
由勾股定理得,,
则,,.
【点睛】
本题考查解直角三角形,解题的关键是利用勾股定理求出AB的长.
19.(1)75°;(2)
【解析】
【分析】
(1)如图:过点A作于点E,在Rt△ABC中运用三角函数可得,即、进一步可得∠EAC=30°,再结合即可解答;
(2)先根据题意求得DE=AE=,然后在Rt△ACE中解直角三角形求得CE,最后利用CD=CE+DE进行计算即可.
【详解】
(1)如图:过点A作于点E,
∵在Rt△ABC中,
∵AE//BC
;
(2)∵在RtAED中,AE=BC=,∠DAE=45°
∴DE=AE=
∵在Rt△ACE中,∠CAE=30°
∴CE=tan30°·AE=30
.
【点睛】
本题主要考查了运用三角函数值求角的大小和解直角三角形,灵活应用三角函数知识是解答本题的关键.
20.(1);(2);(3)存在.
【解析】
【分析】
(1)由 ,且AB=6即可求出AO的长,再由勾股定理即可求出BO的长,即可求出A和B点坐标.
(2)P点从原点出发,在到达终点前,直线l扫过的面积始终为平行四边形BMNE,故求该平行四边的底BE和高OP,相乘即得到面积S;由,且AB=6,可求出AC=10,过D点作DF⊥x轴,易证,求出CF=AO,进而求出OF的长;由,故,求出OE的长,进而求出OB+OE=BE.
(3)分类讨论,当B为直角顶角时,过Q1点作QH⊥y轴,此时△Q1HB≌△BOC,即可求出Q1的坐标;当Q2为直角顶角时,过Q2点作QM⊥y轴,QN⊥x轴,此时Q2MB≌Q2NC,即可求出Q2的坐标.
【详解】
解:(1)由题意可得
故答案为:
(2)过点作轴,垂足为 F ,则
∴
∵
∴,故,求得
.
当时,直线 扫过的图形是平行四边形,
故答案为:.
存在,.如下图所示:
情况一:当B为直角顶角时,此时BQ1=BC,过Q1点作Q1H1⊥y轴于H1,
∴∠Q1H1B=∠BOC=90°,且BQ1=BC,
∵∠Q1BC=90°
∴∠H1BQ1+∠OBC=90°
又∠BCO+∠OBC=90°
∴∠H1BO1=∠BCO
在△Q1H1B和△BOC中:
,∴△△Q1H1B≌△BOC(AAS)
∴Q1H1=BO=,BH1=OC=,∴OH1=
∴
情况二:当Q2为直角顶角时,此时有Q2B=Q2C,
过Q2点分别作Q2M⊥y轴,Q2N⊥x轴
∴∠MQ2B+∠BQ2N=90°
又∴∠NQ2C+∠BQ2N=90°
∴∠MQ2B =∠NQ2C
在△MQ2B和△NQ2C中
,∴△MQ2B≌△NQ2C(AAS)
∴MQ2= NQ2=OM=ON,且∠MON=90°
∴四边形Q2MON为正方形,设MB=NC=a
则OC-a=ON=OB=,且OC=
∴求得a=,∴ON=OM=OB+a=
∴
故答案为:和
【点睛】
本题考查了三角函数求值、平行四边形的面积公式、三角形全等、等腰直角三角形等相关知识,利用锐角相等,其对应的三角函数值相同,可列出比例求解未知线段长.
