【精选备课】2022-2023学年沪教版(上海)数学九年级第一学期 25.4解直角三角形的应用 学案(无答案)
文档属性
| 名称 | 【精选备课】2022-2023学年沪教版(上海)数学九年级第一学期 25.4解直角三角形的应用 学案(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 51.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-28 13:04:19 | ||
图片预览

文档简介
25.4解直角三角形的应用
学习目标
1.理解坡度有关的概念,学会利用已学过的知识解决有关坡度的实际问题;
2.形成分析问题、解决问题的能力和运用数学的意识,感悟数学来于实践又作用于实践.体验数学的价值.
教学过程设计
有关仰角、俯角的实际应用问题
(一)典例分析、学一学
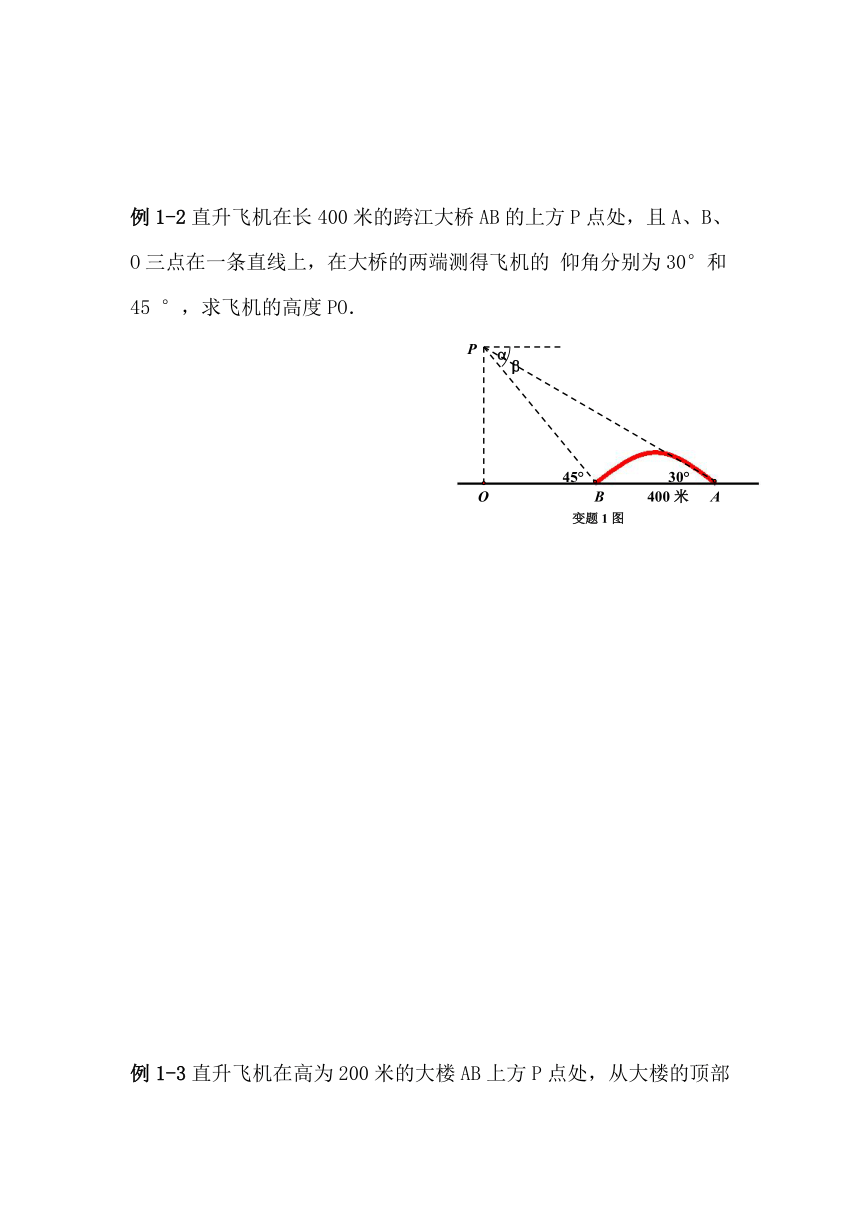
例1-1直升飞机在跨江大桥AB的上方P点处,此时飞机离地面的高度PO=450米,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为α=30°,β=45°,求大桥的长AB.
例1-2直升飞机在长400米的跨江大桥AB的上方P点处,且A、B、O三点在一条直线上,在大桥的两端测得飞机的 仰角分别为30°和45 °,求飞机的高度PO.
例1-3直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机的高度PO.
问题拓展
有一段防洪大堤, 其横断面为梯形ABCD,AB∥CD, 斜坡AD的坡度i1=1∶1.2,斜坡BC的坡度i2=1∶0.8, 大堤顶宽DC为6米, 为了增强抗洪能力, 现将大堤加高, 加高部分的横断面为梯形DCFE, EF∥DC, 点E、F分别在AD、BC的延长线上(如图).当新大堤顶宽EF为3.8米时,大堤加高了几米
巩固练习
1.如图,防洪大堤的横断面是梯形,坝高AC等于6米,背水坡AB的坡度i=1:2,则斜坡AB的长为_______米(精确到0.1米).
2.如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度i=1:,斜坡BD的长是50米,在山坡的坡底处测得铁架顶端A的仰角为45°,在山坡的坡项D处测得铁架顶端A的仰角为60°.
(1)求小山的高度;
(2)求铁架的高度.(≈1.73,精确到0.1米)
P
O
B
A
450米
例1图
P
O
B
A
45°
30°
400米
变题1图
30°
45°
200米
P
O
B
A
变题2图
学习目标
1.理解坡度有关的概念,学会利用已学过的知识解决有关坡度的实际问题;
2.形成分析问题、解决问题的能力和运用数学的意识,感悟数学来于实践又作用于实践.体验数学的价值.
教学过程设计
有关仰角、俯角的实际应用问题
(一)典例分析、学一学
例1-1直升飞机在跨江大桥AB的上方P点处,此时飞机离地面的高度PO=450米,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为α=30°,β=45°,求大桥的长AB.
例1-2直升飞机在长400米的跨江大桥AB的上方P点处,且A、B、O三点在一条直线上,在大桥的两端测得飞机的 仰角分别为30°和45 °,求飞机的高度PO.
例1-3直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机的高度PO.
问题拓展
有一段防洪大堤, 其横断面为梯形ABCD,AB∥CD, 斜坡AD的坡度i1=1∶1.2,斜坡BC的坡度i2=1∶0.8, 大堤顶宽DC为6米, 为了增强抗洪能力, 现将大堤加高, 加高部分的横断面为梯形DCFE, EF∥DC, 点E、F分别在AD、BC的延长线上(如图).当新大堤顶宽EF为3.8米时,大堤加高了几米
巩固练习
1.如图,防洪大堤的横断面是梯形,坝高AC等于6米,背水坡AB的坡度i=1:2,则斜坡AB的长为_______米(精确到0.1米).
2.如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度i=1:,斜坡BD的长是50米,在山坡的坡底处测得铁架顶端A的仰角为45°,在山坡的坡项D处测得铁架顶端A的仰角为60°.
(1)求小山的高度;
(2)求铁架的高度.(≈1.73,精确到0.1米)
P
O
B
A
450米
例1图
P
O
B
A
45°
30°
400米
变题1图
30°
45°
200米
P
O
B
A
变题2图
