人教A版(2019)数学必修第二册8_4_1平面课件(共35张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第二册8_4_1平面课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-28 18:40:10 | ||
图片预览






文档简介
(共35张PPT)
平 面
本节目标
学 习 目 标 核 心 素 养
1.了解平面的概念,掌握平面的画法及表示方法.(难点) 2.能用符号语言描述空间点、直线、平面之间的位置关系.(重点) 3.能用图形、文字、符号三种语言描述三个公理,理解三个公理的地位与作用.(难点、易错点) 1.通过对平面有关概念的学习,培养直观想象的数学素养.
2.通过平面基本性质的应用,培养逻辑推理、直观想象的数学素养.
课前预习
预习课本P124~127,思考并完成下列问题
1.平面的表示方法有哪些?
2.基本事实1、基本事实2、基本事实3的内容是什么?
3.推论1、推论2、推论3各自的作用是什么?
课前小测
1.用符号表示“点A在直线l上,l在平面α外”,正确的是( )
A.A∈l,l α B.A∈l,l α
C.A l,l α D.A l,l α
B
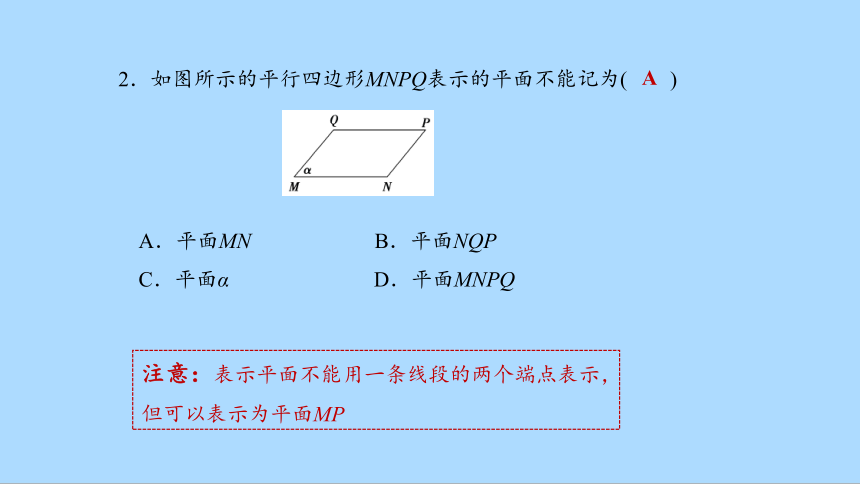
2.如图所示的平行四边形MNPQ表示的平面不能记为( )
A.平面MN B.平面NQP
C.平面α D.平面MNPQ
A
注意:表示平面不能用一条线段的两个端点表示,但可以表示为平面MP
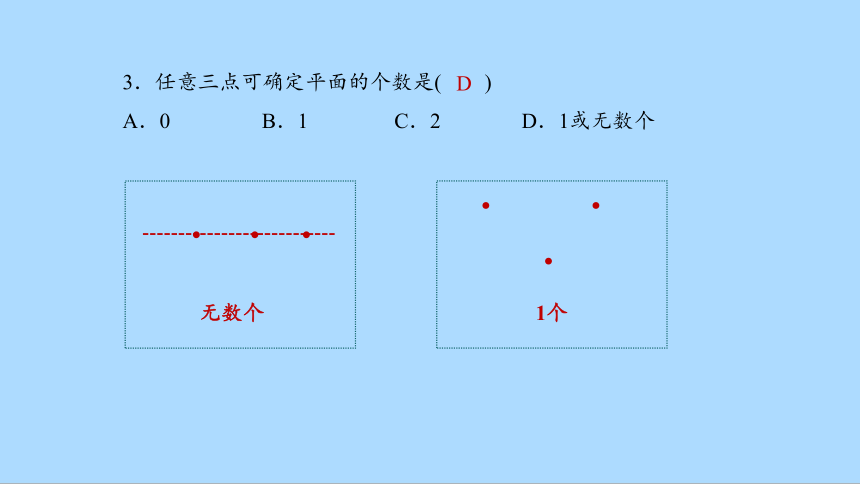
3.任意三点可确定平面的个数是( )
A.0 B.1 C.2 D.1或无数个
D
无数个
1个
考点精讲
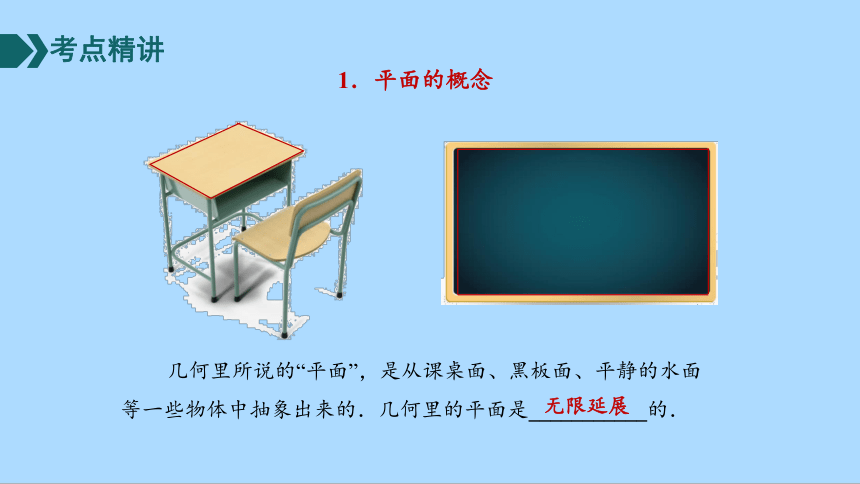
1.平面的概念
几何里所说的“平面”,是从课桌面、黑板面、平静的水面等一些物体中抽象出来的.几何里的平面是___________的.
无限延展
思考1:一个平面能否把空间分成两部分?
提示: 因为平面是无限延展的,一个平面可以把空间分成两部分.
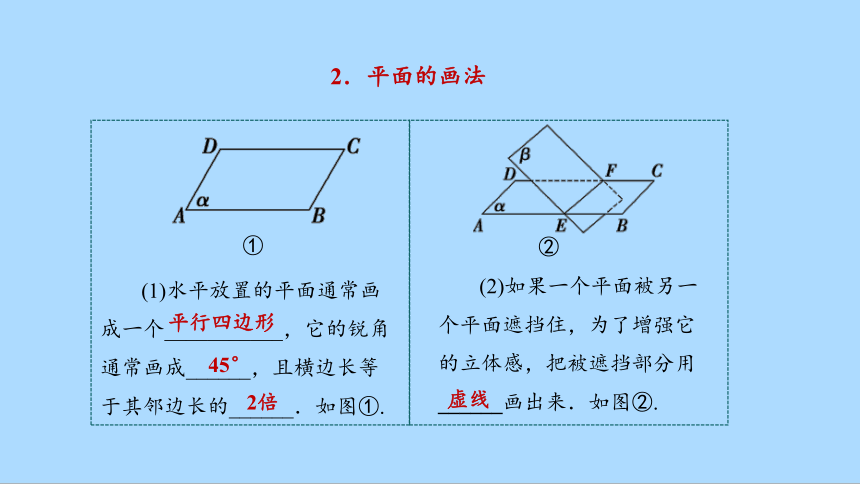
2.平面的画法
(1)水平放置的平面通常画成一个___________,它的锐角通常画成______,且横边长等于其邻边长的______.如图①.
①
②
(2)如果一个平面被另一个平面遮挡住,为了增强它的立体感,把被遮挡部分用______画出来.如图②.
平行四边形
45°
2倍
虚线
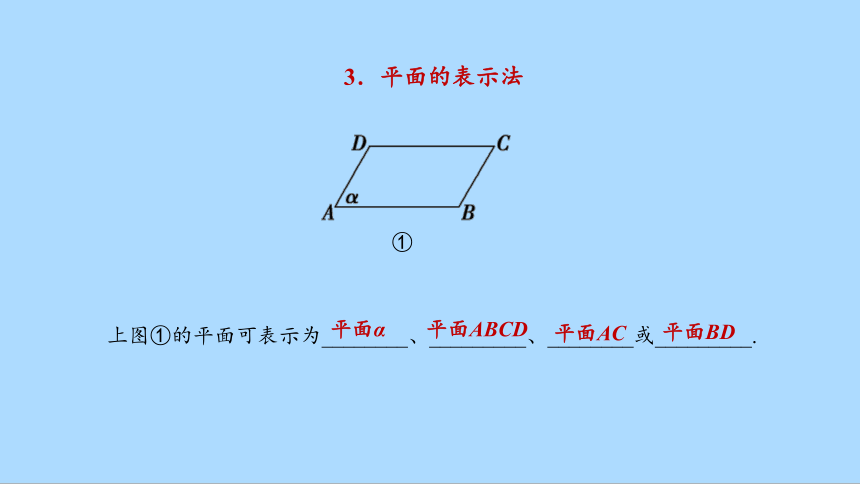
3.平面的表示法
上图①的平面可表示为________、_________、________或_________.
①
平面α
平面ABCD
平面AC
平面BD
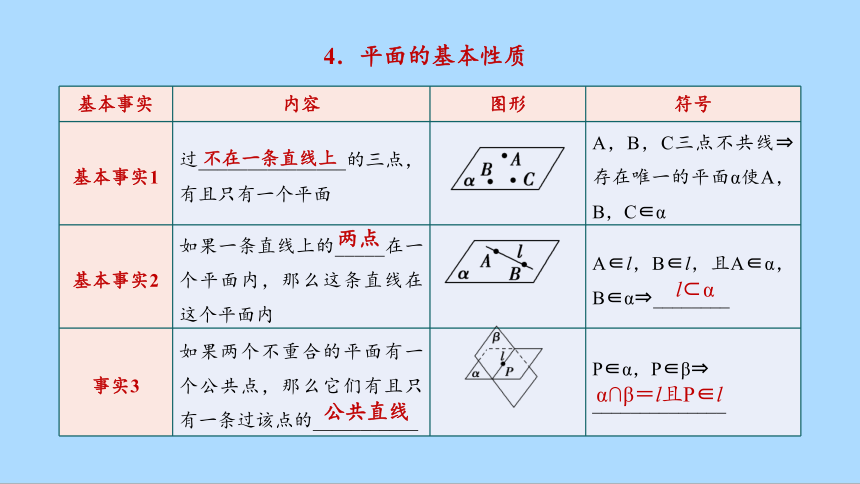
4.平面的基本性质
基本事实 内容 图形 符号
基本事实1 过_______________的三点,有且只有一个平面 A,B,C三点不共线 存在唯一的平面α使A,B,C∈α
基本事实2 如果一条直线上的_____在一个平面内,那么这条直线在这个平面内 A∈l,B∈l,且A∈α,B∈α ________
事实3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的___________ P∈α,P∈β
______________
不在一条直线上
两点
l α
公共直线
α∩β=l且P∈l
思考2:经过空间任意三点能确定一个平面吗?
提示: 不一定,只有经过空间不共线的三点才能确定一个平面.
推论1:经过一条直线和_____________,有且只有一个平面.
推论2:经过两条_______直线,有且只有一个平面.
推论3:经过两条_______直线,有且只有一个平面.
相交
直线外一点
5.推论
平行
题型一 立体几何三种语言的相互转化
典例剖析
【例1】 用符号表示下列语句,并画出图形.
(1)平面α与β相交于直线l,直线a与α,β分别相交于点A,B;
用符号表示:α∩β=l,a∩α=A,a∩β=B
【例1】 用符号表示下列语句,并画出图形.
(2)点A,B在平面α内,直线a与平面α交于点C,点C不在直线AB上.
用符号表示:A∈α,B∈α,a∩α=C,C AB,如图.
方法技巧
(1)用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何,试着用文字语言表示,再用符号语言表示.
(2)要注意符号语言的意义. 如点与直线的位置关系只能用“∈”或“ ”,直线与平面的位置关系只能用“ ”或“ ”.
(3)由符号语言或文字语言画相应的图形时,要注意实线和虚线的区别.
三种语言的转换方法
活学活用
1.用符号语言表示下列语句,并画出图形:
(1)三个平面α,β,γ相交于一点P,且平面α与平面β相交于PA,平面α与平面γ相交于PB,平面β与平面γ相交于PC;
符号语言表示:α∩β∩γ=P,α∩β=PA,α∩γ=PB,β∩γ=PC,图形表示:如图①.
1.用符号语言表示下列语句,并画出图形:
(2)平面ABD与平面BDC相交于BD,平面ABC与平面ADC相交于AC.
平面ABD∩平面BDC=BD,平面ABC∩平面ADC=AC,图形表示:如图②.
题型二 点线共面问题
【例2】 如图,已知:a α,b α,a∩b=A,P∈b,PQ∥a,求证:PQ α.
PQ∥a
PQ 与 a 确定一个平面β
直线a β,点 P∈β
P∈b,b α
P∈α
a α
α与β重合
PQ α
方法技巧
解决点线共面问题的基本方法
活学活用
2.求证:两两相交且不过同一点的三条直线必在同一个平面内.
已知:AB∩AC=A,AB∩BC=B,AC∩BC=C.
求证:直线AB,BC,AC共面.
因为AC∩AB=A,所以直线AB,AC可确定一个平面α.
因为B∈AB,C∈AC,所以B∈α,C∈α,故BC α.
因此直线AB,BC,AC都在平面α内,
所以直线AB,BC,AC共面.
法一
2.求证:两两相交且不过同一点的三条直线必在同一个平面内.
已知:AB∩AC=A,AB∩BC=B,AC∩BC=C.
求证:直线AB,BC,AC共面.
法二
因为A不在直线BC上,
所以点A和直线BC可确定一个平面α.
因为B∈BC,所以B∈α,又A∈α,所以AB α.
同理AC α,故直线AB,BC,AC共面.
2.求证:两两相交且不过同一点的三条直线必在同一个平面内.
已知:AB∩AC=A,AB∩BC=B,AC∩BC=C.
求证:直线AB,BC,AC共面.
法三
因为A,B,C三点不在同一条直线上,
所以A,B,C三点可以确定一个平面α.
因为A∈α,B∈α,所以AB α,
同理BC α,AC α,
故直线AB,BC,AC共面.
题型三 点共线、线共点问题
[探究问题]
1.如图,在正方体ABCD- A1B1C1D1中,设A1C∩平面ABC1D1=E.能否判断点E在平面A1BCD1内?
[提示] 如图,连接BD1,
∵A1C∩平面ABC1D1=E,
∴E∈A1C,E∈平面ABC1D1.
∵A1C 平面A1BCD1,
∴E∈平面A1BCD1.
2.上述问题中,你能证明B,E,D1三点共线吗?
[提示] 由于平面A1BCD1与平面ABC1D1交于直线BD1,又E∈BD1,根据基本事实3可知B,E,D1三点共线.
【例3】 如图,已知平面α, β, 且α∩β=l. 设梯形ABCD中,AD∥BC,且AB α,CD β.
求证:AB,CD,l共点(相交于一点).
梯形的两腰
找交点
探究交点与面α、 β的位置关系
得结论
【例3】 如图,已知平面α, β, 且α∩β=l. 设梯形ABCD中,AD∥BC,且AB α,CD β.
求证:AB,CD,l共点(相交于一点).
因为梯形ABCD中,AD∥BC,
所以AB,CD是梯形ABCD的两腰.
所以AB,CD必定相交于一点. 设AB∩CD=M.
又因为AB α,CD β,所以M∈α,M∈β. 所以M∈α∩β.
又因为α∩β=l,所以M∈l.
即AB,CD,l共点(相交于一点).
活学活用
3、本例变为:如图所示,在空间四边形各边AD、AB、BC、CD上分别取E、F、G、H四点,如果EF、GH交于一点P,求证:点P在直线BD上.
若EF、GH交于一点P,
则E,F,G,H四点共面,
又因为EF 平面ABD,GH 平面CBD,
平面ABD∩平面CBD=BD,
所以P∈平面ABD,且P∈平面CBD,
由基本事实3可得P∈BD.
方法技巧
选择其中两点确定一条直线
1.证明三点共线的方法
方法一
找出两个平面
证明这三点都是这两个平面的公共点
这些点都在两个平面的交线上
基本事实3
方法二
证明另一点也在此直线上
方法技巧
2.证明三线共点的步骤
得到交线也过此点,从而得到三线共点.
1
2
3
首先说明两条直线共面且交于一点;
说明这个点在另两个平面上,并且这两个平面相交;
随堂检测
1.判断正误
(1)平面是处处平的面.( )
(2)平面是无限延展的.( )
(3)平面的形状是平行四边形.( )
(4)一个平面的厚度可以是0.001 cm.( )
√
√
×
×
2.下列空间图形画法错误的是( )
A
B
C
D
√
√
√
×
遮挡部分应画成虚线
D
3.如果点A在直线a上,而直线a在平面α内,点B在平面α内,则可以表示为( )
A.A a,a α,B∈α
B.A∈a,a α,B∈α
C.A a,a∈α,B α
D.A∈a,a∈α,B∈α
B
4.如图,已知D,E是△ABC的边AC,BC上的点,平面α经过D,E两点,若直线AB与平面α的交点是P,求证:点P在直线DE上.
P∈AB
AB 平面ABC
P∈平面ABC
P∈α
平面ABC∩平面α=DE
P∈直线DE
本课小结
1.立体几何的三种语言
图形语言、符号语言、文字语言是立体几何的三大语言,要准确实现这三种语言的相互转换.
2.三个基本事实的作用
基本事实1——判定点共面、线共面的依据;
基本事实2——判定直线在平面内的依据;
基本事实3——判定点共线、线共点的依据.
首先考虑两个平面的交线,再证有关的点都是这两个平面的公共点. 或先由某两点作一条直线,再证明其他点也在这条直线上.
3.证明几点共线的方法
平 面
本节目标
学 习 目 标 核 心 素 养
1.了解平面的概念,掌握平面的画法及表示方法.(难点) 2.能用符号语言描述空间点、直线、平面之间的位置关系.(重点) 3.能用图形、文字、符号三种语言描述三个公理,理解三个公理的地位与作用.(难点、易错点) 1.通过对平面有关概念的学习,培养直观想象的数学素养.
2.通过平面基本性质的应用,培养逻辑推理、直观想象的数学素养.
课前预习
预习课本P124~127,思考并完成下列问题
1.平面的表示方法有哪些?
2.基本事实1、基本事实2、基本事实3的内容是什么?
3.推论1、推论2、推论3各自的作用是什么?
课前小测
1.用符号表示“点A在直线l上,l在平面α外”,正确的是( )
A.A∈l,l α B.A∈l,l α
C.A l,l α D.A l,l α
B
2.如图所示的平行四边形MNPQ表示的平面不能记为( )
A.平面MN B.平面NQP
C.平面α D.平面MNPQ
A
注意:表示平面不能用一条线段的两个端点表示,但可以表示为平面MP
3.任意三点可确定平面的个数是( )
A.0 B.1 C.2 D.1或无数个
D
无数个
1个
考点精讲
1.平面的概念
几何里所说的“平面”,是从课桌面、黑板面、平静的水面等一些物体中抽象出来的.几何里的平面是___________的.
无限延展
思考1:一个平面能否把空间分成两部分?
提示: 因为平面是无限延展的,一个平面可以把空间分成两部分.
2.平面的画法
(1)水平放置的平面通常画成一个___________,它的锐角通常画成______,且横边长等于其邻边长的______.如图①.
①
②
(2)如果一个平面被另一个平面遮挡住,为了增强它的立体感,把被遮挡部分用______画出来.如图②.
平行四边形
45°
2倍
虚线
3.平面的表示法
上图①的平面可表示为________、_________、________或_________.
①
平面α
平面ABCD
平面AC
平面BD
4.平面的基本性质
基本事实 内容 图形 符号
基本事实1 过_______________的三点,有且只有一个平面 A,B,C三点不共线 存在唯一的平面α使A,B,C∈α
基本事实2 如果一条直线上的_____在一个平面内,那么这条直线在这个平面内 A∈l,B∈l,且A∈α,B∈α ________
事实3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的___________ P∈α,P∈β
______________
不在一条直线上
两点
l α
公共直线
α∩β=l且P∈l
思考2:经过空间任意三点能确定一个平面吗?
提示: 不一定,只有经过空间不共线的三点才能确定一个平面.
推论1:经过一条直线和_____________,有且只有一个平面.
推论2:经过两条_______直线,有且只有一个平面.
推论3:经过两条_______直线,有且只有一个平面.
相交
直线外一点
5.推论
平行
题型一 立体几何三种语言的相互转化
典例剖析
【例1】 用符号表示下列语句,并画出图形.
(1)平面α与β相交于直线l,直线a与α,β分别相交于点A,B;
用符号表示:α∩β=l,a∩α=A,a∩β=B
【例1】 用符号表示下列语句,并画出图形.
(2)点A,B在平面α内,直线a与平面α交于点C,点C不在直线AB上.
用符号表示:A∈α,B∈α,a∩α=C,C AB,如图.
方法技巧
(1)用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何,试着用文字语言表示,再用符号语言表示.
(2)要注意符号语言的意义. 如点与直线的位置关系只能用“∈”或“ ”,直线与平面的位置关系只能用“ ”或“ ”.
(3)由符号语言或文字语言画相应的图形时,要注意实线和虚线的区别.
三种语言的转换方法
活学活用
1.用符号语言表示下列语句,并画出图形:
(1)三个平面α,β,γ相交于一点P,且平面α与平面β相交于PA,平面α与平面γ相交于PB,平面β与平面γ相交于PC;
符号语言表示:α∩β∩γ=P,α∩β=PA,α∩γ=PB,β∩γ=PC,图形表示:如图①.
1.用符号语言表示下列语句,并画出图形:
(2)平面ABD与平面BDC相交于BD,平面ABC与平面ADC相交于AC.
平面ABD∩平面BDC=BD,平面ABC∩平面ADC=AC,图形表示:如图②.
题型二 点线共面问题
【例2】 如图,已知:a α,b α,a∩b=A,P∈b,PQ∥a,求证:PQ α.
PQ∥a
PQ 与 a 确定一个平面β
直线a β,点 P∈β
P∈b,b α
P∈α
a α
α与β重合
PQ α
方法技巧
解决点线共面问题的基本方法
活学活用
2.求证:两两相交且不过同一点的三条直线必在同一个平面内.
已知:AB∩AC=A,AB∩BC=B,AC∩BC=C.
求证:直线AB,BC,AC共面.
因为AC∩AB=A,所以直线AB,AC可确定一个平面α.
因为B∈AB,C∈AC,所以B∈α,C∈α,故BC α.
因此直线AB,BC,AC都在平面α内,
所以直线AB,BC,AC共面.
法一
2.求证:两两相交且不过同一点的三条直线必在同一个平面内.
已知:AB∩AC=A,AB∩BC=B,AC∩BC=C.
求证:直线AB,BC,AC共面.
法二
因为A不在直线BC上,
所以点A和直线BC可确定一个平面α.
因为B∈BC,所以B∈α,又A∈α,所以AB α.
同理AC α,故直线AB,BC,AC共面.
2.求证:两两相交且不过同一点的三条直线必在同一个平面内.
已知:AB∩AC=A,AB∩BC=B,AC∩BC=C.
求证:直线AB,BC,AC共面.
法三
因为A,B,C三点不在同一条直线上,
所以A,B,C三点可以确定一个平面α.
因为A∈α,B∈α,所以AB α,
同理BC α,AC α,
故直线AB,BC,AC共面.
题型三 点共线、线共点问题
[探究问题]
1.如图,在正方体ABCD- A1B1C1D1中,设A1C∩平面ABC1D1=E.能否判断点E在平面A1BCD1内?
[提示] 如图,连接BD1,
∵A1C∩平面ABC1D1=E,
∴E∈A1C,E∈平面ABC1D1.
∵A1C 平面A1BCD1,
∴E∈平面A1BCD1.
2.上述问题中,你能证明B,E,D1三点共线吗?
[提示] 由于平面A1BCD1与平面ABC1D1交于直线BD1,又E∈BD1,根据基本事实3可知B,E,D1三点共线.
【例3】 如图,已知平面α, β, 且α∩β=l. 设梯形ABCD中,AD∥BC,且AB α,CD β.
求证:AB,CD,l共点(相交于一点).
梯形的两腰
找交点
探究交点与面α、 β的位置关系
得结论
【例3】 如图,已知平面α, β, 且α∩β=l. 设梯形ABCD中,AD∥BC,且AB α,CD β.
求证:AB,CD,l共点(相交于一点).
因为梯形ABCD中,AD∥BC,
所以AB,CD是梯形ABCD的两腰.
所以AB,CD必定相交于一点. 设AB∩CD=M.
又因为AB α,CD β,所以M∈α,M∈β. 所以M∈α∩β.
又因为α∩β=l,所以M∈l.
即AB,CD,l共点(相交于一点).
活学活用
3、本例变为:如图所示,在空间四边形各边AD、AB、BC、CD上分别取E、F、G、H四点,如果EF、GH交于一点P,求证:点P在直线BD上.
若EF、GH交于一点P,
则E,F,G,H四点共面,
又因为EF 平面ABD,GH 平面CBD,
平面ABD∩平面CBD=BD,
所以P∈平面ABD,且P∈平面CBD,
由基本事实3可得P∈BD.
方法技巧
选择其中两点确定一条直线
1.证明三点共线的方法
方法一
找出两个平面
证明这三点都是这两个平面的公共点
这些点都在两个平面的交线上
基本事实3
方法二
证明另一点也在此直线上
方法技巧
2.证明三线共点的步骤
得到交线也过此点,从而得到三线共点.
1
2
3
首先说明两条直线共面且交于一点;
说明这个点在另两个平面上,并且这两个平面相交;
随堂检测
1.判断正误
(1)平面是处处平的面.( )
(2)平面是无限延展的.( )
(3)平面的形状是平行四边形.( )
(4)一个平面的厚度可以是0.001 cm.( )
√
√
×
×
2.下列空间图形画法错误的是( )
A
B
C
D
√
√
√
×
遮挡部分应画成虚线
D
3.如果点A在直线a上,而直线a在平面α内,点B在平面α内,则可以表示为( )
A.A a,a α,B∈α
B.A∈a,a α,B∈α
C.A a,a∈α,B α
D.A∈a,a∈α,B∈α
B
4.如图,已知D,E是△ABC的边AC,BC上的点,平面α经过D,E两点,若直线AB与平面α的交点是P,求证:点P在直线DE上.
P∈AB
AB 平面ABC
P∈平面ABC
P∈α
平面ABC∩平面α=DE
P∈直线DE
本课小结
1.立体几何的三种语言
图形语言、符号语言、文字语言是立体几何的三大语言,要准确实现这三种语言的相互转换.
2.三个基本事实的作用
基本事实1——判定点共面、线共面的依据;
基本事实2——判定直线在平面内的依据;
基本事实3——判定点共线、线共点的依据.
首先考虑两个平面的交线,再证有关的点都是这两个平面的公共点. 或先由某两点作一条直线,再证明其他点也在这条直线上.
3.证明几点共线的方法
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
