人教A版(2019)数学必修第二册8_6_2直线与平面垂直课件(共33张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第二册8_6_2直线与平面垂直课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 726.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-28 18:42:29 | ||
图片预览









文档简介
(共33张PPT)
直线与平面垂直
本节目标
学 习 目 标 核 心 素 养
1.了解线面垂直的定义.(重点) 2.理解线面垂直的判定定理,并会运用.(难点) 3.理解直线与平面所成角的概念,并能解决简单的线面角问题.(易错点) 4.能利用线面垂直的判定定理和性质定理进行证明.(重点) 1.通过学习线面垂直的判定定理和性质定理,提升直观想象、逻辑推理的数学素养.
2.通过学习直线与平面所成的角,提升直观想象、数学运算的数学素养.
课前预习
预习课本P149~155,思考并完成以下问题
1.直线与平面垂直的定义是怎样的?
2.直线与平面垂直的判定定理是什么?
3.直线与平面所成的角是怎样定义的?直线与平面所成的角的范围是什么?
4.直线与平面垂直的性质定理是什么?
课前小测
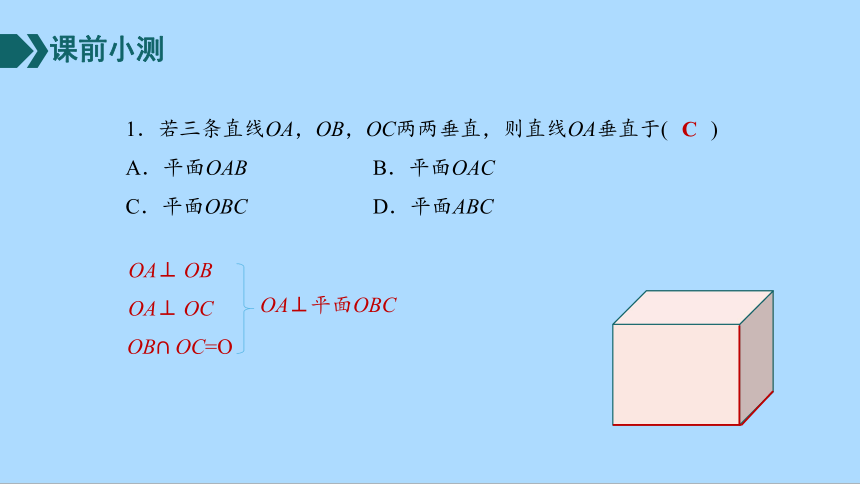
1.若三条直线OA,OB,OC两两垂直,则直线OA垂直于( )
A.平面OAB B.平面OAC
C.平面OBC D.平面ABC
C
OA⊥ OB
OA⊥ OC
OA⊥平面OBC
OB=O
2.已知直线a,b,平面α,且a⊥α,下列条件中,能推出a∥b的是( )
A.b∥α B.b α
C.b⊥α D.b与α相交
C
当b⊥α,a⊥α时,a∥b.
3.一条直线和三角形的两边同时垂直,则这条直线和三角形的第三边的位置关系是( )
A.平行 B.垂直
C .相交不垂直 D .不确定
B
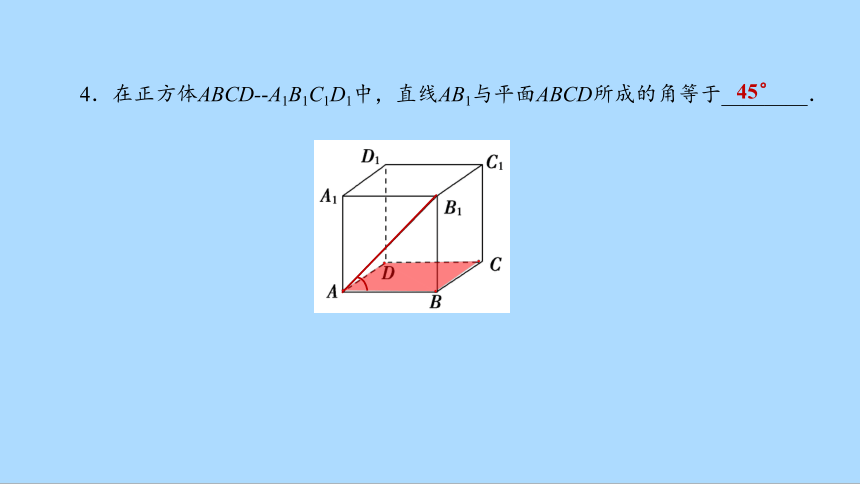
4.在正方体ABCD- A1B1C1D1中,直线AB1与平面ABCD所成的角等于________.
45°
考点精讲
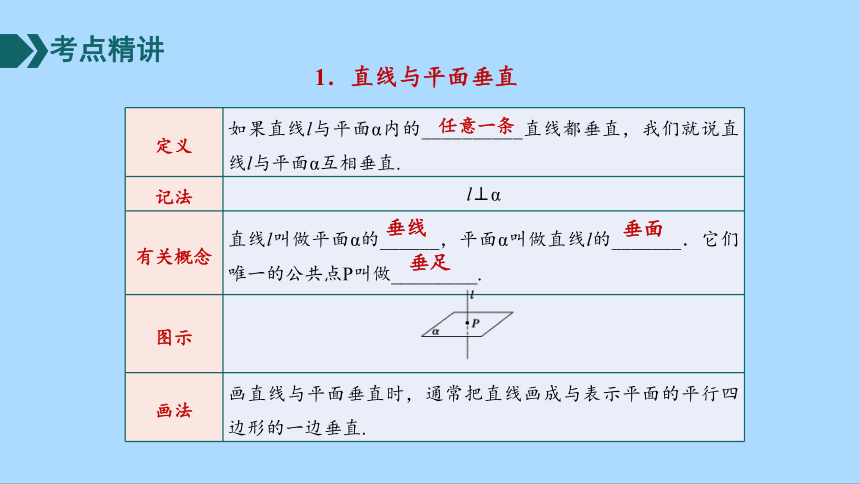
1.直线与平面垂直
定义 如果直线l与平面α内的__________直线都垂直,我们就说直线l与平面α互相垂直.
记法 l⊥α
有关概念 直线l叫做平面α的______,平面α叫做直线l的_______.它们唯一的公共点P叫做_________.
图示
画法 画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.
任意一条
垂线
垂面
垂足
2.直线与平面垂直的判定定理
文字语言 如果一条直线与一个平面内的_____________垂直,那么该直线与此平面垂直.
符号语言 l⊥a,l⊥b,a α,b α,_________ l⊥α
图形语言
两条相交直线
a∩b=P
3.直线和平面所成的角
有关概念 对应图形
斜线 一条直线l与一个平面α_____,但不与这个平面α_____,图中__________.
斜足 斜线和平面的_______,图中点A 射影 过斜线上斜足以外的一点P向平面α引_____PO,过____O和_____A的直线AO叫做斜线在这个平面内的射影 直线与平面所成的角 定义:平面的一条斜线和它在平面上的射影所成的角 规定:一条直线垂直于平面,它们所成的角是直角; 一条直线和平面平行或在平面内,它们所成的角是0°的角 取值范围 [0°,90°] 相交
垂直
直线PA
交点
垂线
垂足
斜足
思考1:直线与平面垂直定义中的关键词“任意一条直线”是否可以换成“所有直线”“无数条直线”?
提示:定义中的“任意一条直线”与“所有直线”是等效的,但是不可说成“无数条直线”,因为一条直线与某平面内无数条平行直线垂直,该直线与这个平面不一定垂直.
4.直线与平面垂直的性质定理
文字语言 垂直于同一个平面的两条直线________
符号语言 _______
图形语言
作用 ①线面垂直 线线平行
②作平行线
平行
a∥b
思考2:过一点有几条直线与已知平面垂直?
提示:有且仅有一条.假设过一点有两条直线与已知平面垂直,由直线与平面垂直的性质定理可得这两条直线平行,即无公共点,这与过同一点相矛盾,故只有一条直线.
题型一 直线与平面垂直的判定
典例剖析
【例1】 如图,在三棱锥S -ABC中,∠ABC=90°,D是AC的中点,且SA=SB=SC.
(1)求证:SD⊥平面ABC;
因为SA=SC,D是AC的中点,
所以SD⊥AC.在Rt△ABC中,AD=BD,
由已知SA=SB,
所以△ADS≌△BDS,
所以SD⊥BD.又AC∩BD=D,AC,BD 平面ABC,
所以SD⊥平面ABC.
题型一 直线与平面垂直的判定
典例剖析
【例1】 如图,在三棱锥S -ABC中,∠ABC=90°,D是AC的中点,且SA=SB=SC.
(2)若AB=BC,求证:BD⊥平面SAC.
因为AB=BC,D为AC的中点,
所以BD⊥AC.由(1)知SD⊥BD.
又因为SD∩AC=D,SD,AC 平面SAC,
所以BD⊥平面SAC.
方法技巧
证线面垂直的方法
(1)线线垂直证明线面垂直
①定义法 (不常用,但由线面垂直可得出线线垂直);
②判定定理最常用:
要着力寻找平面内哪两条相交直线(有时作辅助线);
结合平面图形的性质(如勾股定理逆定理、等腰三角形底边中线等)及一条直线与平行线中一条垂直,也与另一条垂直等结论来论证线线垂直.
方法技巧
证线面垂直的方法
(2)平行转化法(利用推论):
①a∥b,a⊥α b⊥α;
②α∥β,a⊥α a⊥β.
活学活用
1.如图,AB是圆O的直径,PA垂直于圆O所在的平面,M是圆周上任意一点,AN⊥PM,垂足为N. 求证:AN⊥平面PBM.
设圆O所在的平面为α,∵PA⊥α,且BM α,
∴PA⊥BM.
又∵AB为⊙O的直径,点M为圆周上一点,
∴AM⊥BM. 由于直线PA∩AM=A,
∴BM⊥平面PAM,而AN 平面PAM,∴BM⊥AN.
∴AN与PM、BM两条相交直线互相垂直.
故AN⊥平面PBM.
题型二 直线与平面所成的角
1.若图中的∠POA是斜线PO与平面α所成的角,则需具备哪些条件?
[探究问题]
[提示] 需要PA⊥α,A为垂足,OA为斜线PO的射影,这样∠POA就是斜线PO与平面α所成的角.
2.空间几何体中,确定线面角的关键是什么?
[探究问题]
[提示] 在空间几何体中确定线面角时,过斜线上一点向平面作垂线,确定垂足位置是关键,垂足确定,则射影确定,线面角确定.
【例2】 在正方体ABCD -A1B1C1D1中,
(1)求直线A1C与平面ABCD所成的角的正切值;
∵直线A1A⊥平面ABCD,
∴∠A1CA为直线A1C与平面ABCD所成的角,
设A1A=1,则AC= ,
∴tan∠A1CA= .
【例2】 在正方体ABCD -A1B1C1D1中,
(2)求直线A1B与平面BDD1B1所成的角.
在正方形A1B1C1D1中,A1C1⊥B1D1,
∵BB1⊥平面A1B1C1D1,A1C1 平面A1B1C1D1,
∴BB1⊥A1C1,又BB1∩B1D1=B1,
∴A1C1⊥平面BDD1B1,垂足为O.
∴∠A1BO为直线A1B与平面BDD1B1所成的角,
在Rt△A1BO中,A1O=A1C1= A1B,∠A1BO=30°,
即A1B与平面BDD1B1所成的角为30°.
活学活用
2. 在本例正方体中,若E为棱AB的中点,求直线B1E与平面BB1D1D所成角的正切值.
O
O1
过E作EO1∥AC交BD于点O1,易证AC⊥平面BB1D1D,
∴EO1⊥平面BB1D1D,∴B1O1是B1E在平面BB1D1D内的射影,
∴∠EB1O1为B1E与平面BB1D1D所成的角.
设正方体的棱长为a,∵E是AB的中点,EO1∥AC,
∴O1是BO的中点,
方法技巧
求斜线与平面所成角的步骤
作图
证明
计算
作(或找)出斜线在平面内的射影,作射影要过斜线上一点作平面的垂线,再过垂足和斜足作直线,注意斜线上点的选取以及垂足的位置要与问题中已知量有关,才能便于计算.
证明某平面角就是斜线与平面所成的角.
通常在垂线段、斜线和射影所组成的直角三角形中计算.
题型三 线面垂直性质定理的应用
【例3】 如图所示,在正方体ABCD- A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC. 求证:MN∥AD1.
因为四边形ADD1A1为正方形,
所以AD1⊥A1D.
又因为CD⊥平面ADD1A1,
所以CD⊥AD1.
因为A1D∩CD=D,
所以AD1⊥平面A1DC.
又因为MN⊥平面A1DC,所以MN∥AD1.
方法技巧
(1)利用线线平行定义:证共面且无公共点;
(2)利用三线平行公理:证两线同时平行于第三条直线;
(3)利用线面平行的性质定理:把证线线平行转化为证线面平行;
(4)利用线面垂直的性质定理:把证线线平行转化为证线面垂直;
(5)利用面面平行的性质定理:把证线线平行转化为证面面平行.
证明线线平行常用方法
活学活用
3.如图,已知平面α∩平面β=l,EA⊥α,垂足为A,EB⊥β,直线a β,a⊥AB. 求证:a∥l.
因为EA⊥α,α∩β=l,即l α,所以l⊥EA.
同理 l⊥EB. 又EA∩EB=E,所以 l⊥平面EAB.
因为EB⊥β,a β,所以 EB⊥a,
又a⊥AB,EB∩AB=B,
所以 a⊥平面EAB.
由线面垂直的性质定理,得a∥l.
随堂检测
1.直线l⊥平面α,直线m α,则l与m不可能( )
A.平行 B.相交 C.异面 D.垂直
A
若l∥m,l α,m α,则l∥α,这与已知l⊥α矛盾.
所以直线l与m不可能平行.
2.垂直于梯形两腰的直线与梯形所在平面的位置关系是( )
A.垂直 B.相交但不垂直
C.平行 D.不确定
A
因为梯形两腰所在直线为两条相交直线,
所以由线面垂直的判定定理知,直线与平面垂直.
3.如图所示,若斜线段AB是它在平面α上的射影BO的2倍,则AB与平面α所成的角是( )
A.60° B.45°
C.30° D.120°
A
1
2
60°
4.在正方体ABCD- A1B1C1D1中,求证:A1C⊥平面BC1D.
如图,连接AC,∴ AC⊥BD,
又∵BD⊥A1A,AC∩AA1=A,AC,A1A 平面A1AC,
∴BD⊥平面A1AC,∵A1C 平面A1AC,
∴ BD⊥A1C.
同理可证 BC1⊥A1C.
又∵BD∩BC1=B,BD,BC1 平面BC1D,
∴A1C⊥平面BC1D.
本课小结
1.线线垂直和线面垂直的相互转化
(1)线面垂直的定义.
(2)线面垂直的判定定理.
(3)如果两条平行直线的一条直线垂直于一个平面,那么另一条直线也垂直于这个平面.
(4)如果一条直线垂直于两个平行平面中的一个平面,那么它也垂直于另一个平面.
2.证明线面垂直的方法
直线与平面垂直
本节目标
学 习 目 标 核 心 素 养
1.了解线面垂直的定义.(重点) 2.理解线面垂直的判定定理,并会运用.(难点) 3.理解直线与平面所成角的概念,并能解决简单的线面角问题.(易错点) 4.能利用线面垂直的判定定理和性质定理进行证明.(重点) 1.通过学习线面垂直的判定定理和性质定理,提升直观想象、逻辑推理的数学素养.
2.通过学习直线与平面所成的角,提升直观想象、数学运算的数学素养.
课前预习
预习课本P149~155,思考并完成以下问题
1.直线与平面垂直的定义是怎样的?
2.直线与平面垂直的判定定理是什么?
3.直线与平面所成的角是怎样定义的?直线与平面所成的角的范围是什么?
4.直线与平面垂直的性质定理是什么?
课前小测
1.若三条直线OA,OB,OC两两垂直,则直线OA垂直于( )
A.平面OAB B.平面OAC
C.平面OBC D.平面ABC
C
OA⊥ OB
OA⊥ OC
OA⊥平面OBC
OB=O
2.已知直线a,b,平面α,且a⊥α,下列条件中,能推出a∥b的是( )
A.b∥α B.b α
C.b⊥α D.b与α相交
C
当b⊥α,a⊥α时,a∥b.
3.一条直线和三角形的两边同时垂直,则这条直线和三角形的第三边的位置关系是( )
A.平行 B.垂直
C .相交不垂直 D .不确定
B
4.在正方体ABCD- A1B1C1D1中,直线AB1与平面ABCD所成的角等于________.
45°
考点精讲
1.直线与平面垂直
定义 如果直线l与平面α内的__________直线都垂直,我们就说直线l与平面α互相垂直.
记法 l⊥α
有关概念 直线l叫做平面α的______,平面α叫做直线l的_______.它们唯一的公共点P叫做_________.
图示
画法 画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.
任意一条
垂线
垂面
垂足
2.直线与平面垂直的判定定理
文字语言 如果一条直线与一个平面内的_____________垂直,那么该直线与此平面垂直.
符号语言 l⊥a,l⊥b,a α,b α,_________ l⊥α
图形语言
两条相交直线
a∩b=P
3.直线和平面所成的角
有关概念 对应图形
斜线 一条直线l与一个平面α_____,但不与这个平面α_____,图中__________.
斜足 斜线和平面的_______,图中点A 射影 过斜线上斜足以外的一点P向平面α引_____PO,过____O和_____A的直线AO叫做斜线在这个平面内的射影 直线与平面所成的角 定义:平面的一条斜线和它在平面上的射影所成的角 规定:一条直线垂直于平面,它们所成的角是直角; 一条直线和平面平行或在平面内,它们所成的角是0°的角 取值范围 [0°,90°] 相交
垂直
直线PA
交点
垂线
垂足
斜足
思考1:直线与平面垂直定义中的关键词“任意一条直线”是否可以换成“所有直线”“无数条直线”?
提示:定义中的“任意一条直线”与“所有直线”是等效的,但是不可说成“无数条直线”,因为一条直线与某平面内无数条平行直线垂直,该直线与这个平面不一定垂直.
4.直线与平面垂直的性质定理
文字语言 垂直于同一个平面的两条直线________
符号语言 _______
图形语言
作用 ①线面垂直 线线平行
②作平行线
平行
a∥b
思考2:过一点有几条直线与已知平面垂直?
提示:有且仅有一条.假设过一点有两条直线与已知平面垂直,由直线与平面垂直的性质定理可得这两条直线平行,即无公共点,这与过同一点相矛盾,故只有一条直线.
题型一 直线与平面垂直的判定
典例剖析
【例1】 如图,在三棱锥S -ABC中,∠ABC=90°,D是AC的中点,且SA=SB=SC.
(1)求证:SD⊥平面ABC;
因为SA=SC,D是AC的中点,
所以SD⊥AC.在Rt△ABC中,AD=BD,
由已知SA=SB,
所以△ADS≌△BDS,
所以SD⊥BD.又AC∩BD=D,AC,BD 平面ABC,
所以SD⊥平面ABC.
题型一 直线与平面垂直的判定
典例剖析
【例1】 如图,在三棱锥S -ABC中,∠ABC=90°,D是AC的中点,且SA=SB=SC.
(2)若AB=BC,求证:BD⊥平面SAC.
因为AB=BC,D为AC的中点,
所以BD⊥AC.由(1)知SD⊥BD.
又因为SD∩AC=D,SD,AC 平面SAC,
所以BD⊥平面SAC.
方法技巧
证线面垂直的方法
(1)线线垂直证明线面垂直
①定义法 (不常用,但由线面垂直可得出线线垂直);
②判定定理最常用:
要着力寻找平面内哪两条相交直线(有时作辅助线);
结合平面图形的性质(如勾股定理逆定理、等腰三角形底边中线等)及一条直线与平行线中一条垂直,也与另一条垂直等结论来论证线线垂直.
方法技巧
证线面垂直的方法
(2)平行转化法(利用推论):
①a∥b,a⊥α b⊥α;
②α∥β,a⊥α a⊥β.
活学活用
1.如图,AB是圆O的直径,PA垂直于圆O所在的平面,M是圆周上任意一点,AN⊥PM,垂足为N. 求证:AN⊥平面PBM.
设圆O所在的平面为α,∵PA⊥α,且BM α,
∴PA⊥BM.
又∵AB为⊙O的直径,点M为圆周上一点,
∴AM⊥BM. 由于直线PA∩AM=A,
∴BM⊥平面PAM,而AN 平面PAM,∴BM⊥AN.
∴AN与PM、BM两条相交直线互相垂直.
故AN⊥平面PBM.
题型二 直线与平面所成的角
1.若图中的∠POA是斜线PO与平面α所成的角,则需具备哪些条件?
[探究问题]
[提示] 需要PA⊥α,A为垂足,OA为斜线PO的射影,这样∠POA就是斜线PO与平面α所成的角.
2.空间几何体中,确定线面角的关键是什么?
[探究问题]
[提示] 在空间几何体中确定线面角时,过斜线上一点向平面作垂线,确定垂足位置是关键,垂足确定,则射影确定,线面角确定.
【例2】 在正方体ABCD -A1B1C1D1中,
(1)求直线A1C与平面ABCD所成的角的正切值;
∵直线A1A⊥平面ABCD,
∴∠A1CA为直线A1C与平面ABCD所成的角,
设A1A=1,则AC= ,
∴tan∠A1CA= .
【例2】 在正方体ABCD -A1B1C1D1中,
(2)求直线A1B与平面BDD1B1所成的角.
在正方形A1B1C1D1中,A1C1⊥B1D1,
∵BB1⊥平面A1B1C1D1,A1C1 平面A1B1C1D1,
∴BB1⊥A1C1,又BB1∩B1D1=B1,
∴A1C1⊥平面BDD1B1,垂足为O.
∴∠A1BO为直线A1B与平面BDD1B1所成的角,
在Rt△A1BO中,A1O=A1C1= A1B,∠A1BO=30°,
即A1B与平面BDD1B1所成的角为30°.
活学活用
2. 在本例正方体中,若E为棱AB的中点,求直线B1E与平面BB1D1D所成角的正切值.
O
O1
过E作EO1∥AC交BD于点O1,易证AC⊥平面BB1D1D,
∴EO1⊥平面BB1D1D,∴B1O1是B1E在平面BB1D1D内的射影,
∴∠EB1O1为B1E与平面BB1D1D所成的角.
设正方体的棱长为a,∵E是AB的中点,EO1∥AC,
∴O1是BO的中点,
方法技巧
求斜线与平面所成角的步骤
作图
证明
计算
作(或找)出斜线在平面内的射影,作射影要过斜线上一点作平面的垂线,再过垂足和斜足作直线,注意斜线上点的选取以及垂足的位置要与问题中已知量有关,才能便于计算.
证明某平面角就是斜线与平面所成的角.
通常在垂线段、斜线和射影所组成的直角三角形中计算.
题型三 线面垂直性质定理的应用
【例3】 如图所示,在正方体ABCD- A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC. 求证:MN∥AD1.
因为四边形ADD1A1为正方形,
所以AD1⊥A1D.
又因为CD⊥平面ADD1A1,
所以CD⊥AD1.
因为A1D∩CD=D,
所以AD1⊥平面A1DC.
又因为MN⊥平面A1DC,所以MN∥AD1.
方法技巧
(1)利用线线平行定义:证共面且无公共点;
(2)利用三线平行公理:证两线同时平行于第三条直线;
(3)利用线面平行的性质定理:把证线线平行转化为证线面平行;
(4)利用线面垂直的性质定理:把证线线平行转化为证线面垂直;
(5)利用面面平行的性质定理:把证线线平行转化为证面面平行.
证明线线平行常用方法
活学活用
3.如图,已知平面α∩平面β=l,EA⊥α,垂足为A,EB⊥β,直线a β,a⊥AB. 求证:a∥l.
因为EA⊥α,α∩β=l,即l α,所以l⊥EA.
同理 l⊥EB. 又EA∩EB=E,所以 l⊥平面EAB.
因为EB⊥β,a β,所以 EB⊥a,
又a⊥AB,EB∩AB=B,
所以 a⊥平面EAB.
由线面垂直的性质定理,得a∥l.
随堂检测
1.直线l⊥平面α,直线m α,则l与m不可能( )
A.平行 B.相交 C.异面 D.垂直
A
若l∥m,l α,m α,则l∥α,这与已知l⊥α矛盾.
所以直线l与m不可能平行.
2.垂直于梯形两腰的直线与梯形所在平面的位置关系是( )
A.垂直 B.相交但不垂直
C.平行 D.不确定
A
因为梯形两腰所在直线为两条相交直线,
所以由线面垂直的判定定理知,直线与平面垂直.
3.如图所示,若斜线段AB是它在平面α上的射影BO的2倍,则AB与平面α所成的角是( )
A.60° B.45°
C.30° D.120°
A
1
2
60°
4.在正方体ABCD- A1B1C1D1中,求证:A1C⊥平面BC1D.
如图,连接AC,∴ AC⊥BD,
又∵BD⊥A1A,AC∩AA1=A,AC,A1A 平面A1AC,
∴BD⊥平面A1AC,∵A1C 平面A1AC,
∴ BD⊥A1C.
同理可证 BC1⊥A1C.
又∵BD∩BC1=B,BD,BC1 平面BC1D,
∴A1C⊥平面BC1D.
本课小结
1.线线垂直和线面垂直的相互转化
(1)线面垂直的定义.
(2)线面垂直的判定定理.
(3)如果两条平行直线的一条直线垂直于一个平面,那么另一条直线也垂直于这个平面.
(4)如果一条直线垂直于两个平行平面中的一个平面,那么它也垂直于另一个平面.
2.证明线面垂直的方法
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
