16.1 二次根式的概念和性质(练习巩固)(含解析)
文档属性
| 名称 | 16.1 二次根式的概念和性质(练习巩固)(含解析) |
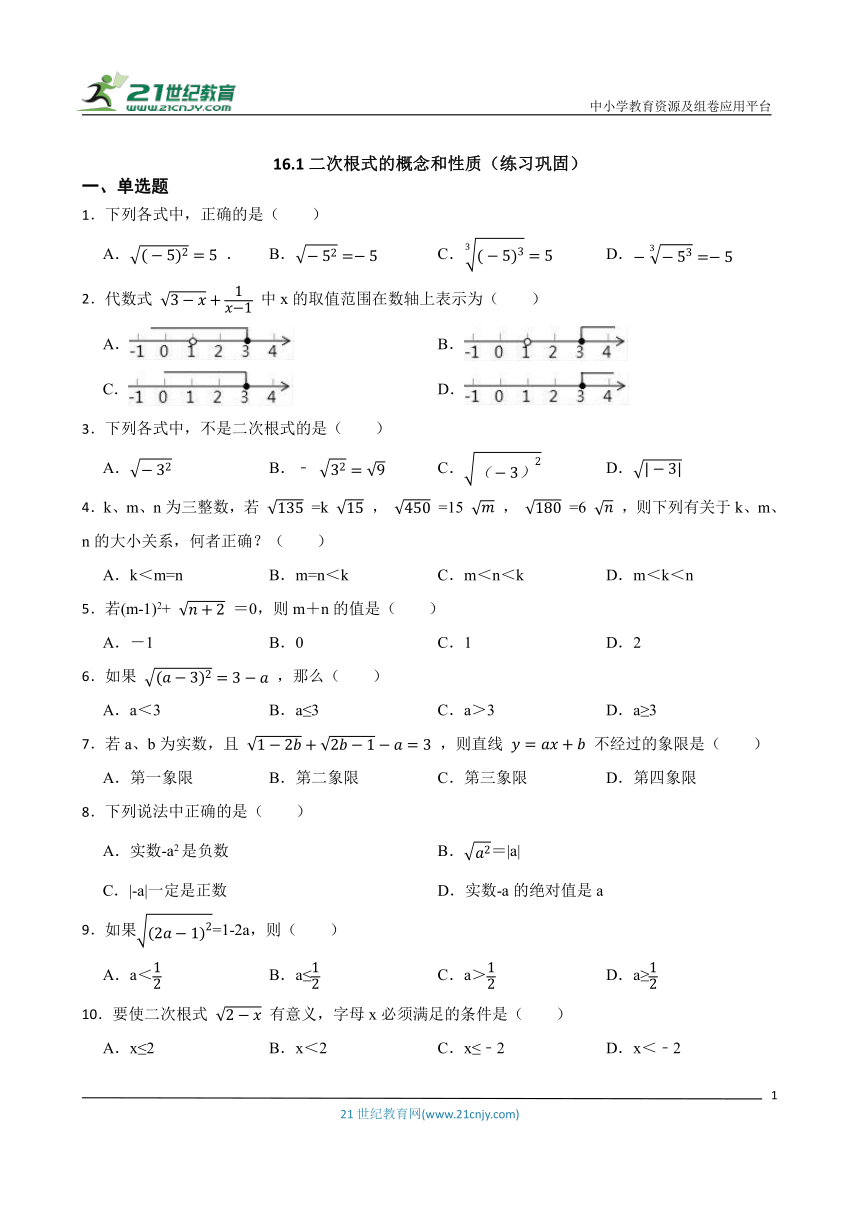
|
|
| 格式 | docx | ||
| 文件大小 | 992.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-16 00:00:00 | ||
图片预览
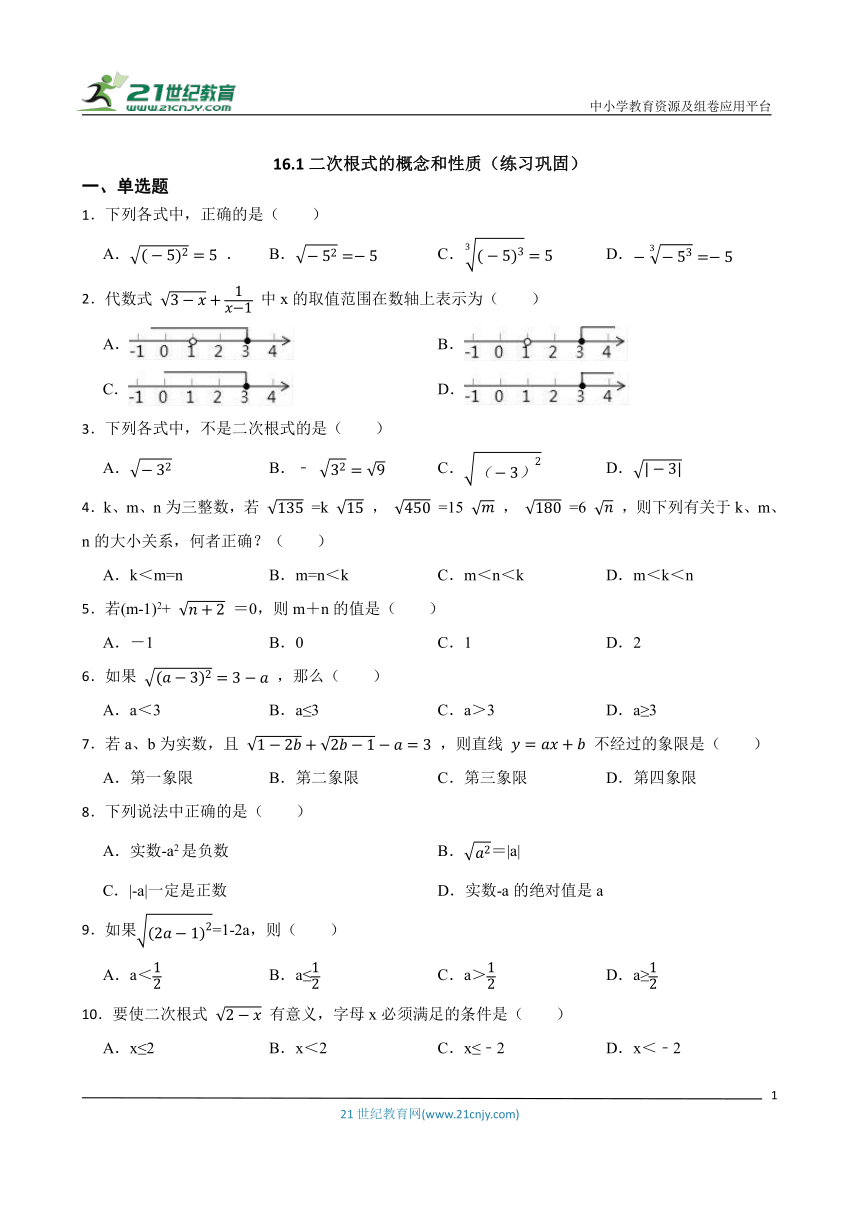



文档简介
中小学教育资源及组卷应用平台
16.1二次根式的概念和性质(练习巩固)
一、单选题
1.下列各式中,正确的是( )
A. . B. C. D.
2.代数式 中x的取值范围在数轴上表示为( )
A. B.
C. D.
3.下列各式中,不是二次根式的是( )
A. B.﹣ C. D.
4.k、m、n为三整数,若 =k , =15 , =6 ,则下列有关于k、m、n的大小关系,何者正确?( )
A.k<m=n B.m=n<k C.m<n<k D.m<k<n
5.若(m-1)2+ =0,则m+n的值是( )
A.-1 B.0 C.1 D.2
6.如果 ,那么( )
A.a<3 B.a≤3 C.a>3 D.a≥3
7.若a、b为实数,且 ,则直线 不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.下列说法中正确的是( )
A.实数-a2是负数 B.=|a|
C.|-a|一定是正数 D.实数-a的绝对值是a
9.如果=1-2a,则( )
A.a< B.a≤ C.a> D.a≥
10.要使二次根式 有意义,字母x必须满足的条件是( )
A.x≤2 B.x<2 C.x≤﹣2 D.x<﹣2
二、填空题
11.使代数式 有意义的x的取值范围是 .
12.已知则ab= .
13. 是整数,则正整数n的最小值是 .
14.a、b为实数,在数轴上的位置如图所示,则 + 的值是 .
15.若代数式 有意义,则a的取值范围是 .
三、解答题
16.若x,y都是实数,且y=++1,求+3y的值.
17.已知 =﹣a,求 ﹣|1﹣2a|的值.
18.已知数a,b,c在数轴上的位置如图所示:
化简:
19.(1)已知y=﹣+8x,求的平方根.
(2)当﹣4<x<1时,化简﹣2.
20.已知实数x、y满足x2﹣12x+ +36=0,求 的值.
参考答案
1.【答案】A
【解析】解:A、 ,故此选项符合题意;
B、 ,无意义,故此选项不符合题意;
C、 ,故此选项不符合题意;
D、 ,故此选项不符合题意;
故答案为:A.
2.【答案】A
【解析】由题意,得:3﹣x≥0且x﹣1≠0,解得:x≤3且x≠1,在数轴上表示如图:
.
故答案为:A.
3.【答案】A
【解析】解:A、 ,不是二次根式;
B、﹣ ,是二次根式;
C、 ,是二次根式;
D、 ,是二次根式;
故选:A.
4.【答案】D
【解析】解: =3 , =15 , =6 ,
可得:k=3,m=2,n=5,
则m<k<n.
故选:D
5.【答案】A
【解析】∵(m-1)2+ =0
∴m 1=0,n+2=0;
∴m=1,n= 2,
∴m+n=1+( 2)= 1
故答案为:A.
6.【答案】B
【解析】解:∵ ,
∴3-a≥0,
∴a≤3,
故答案为:B.
7.【答案】C
【解析】解: 、 为实数,且 ,
,
解得, ,
,
,
直线 可以写成 ,
直线 经过第一、二、四象限,不经过第三象限,
直线 不经过的象限是第三象限,
故答案为:C.
8.【答案】B
【解析】A、实数-a2是负数,a=0时不成立,故选项错误;
B、=|a|,符合二次根式的意义,故选项正确,
C、|-a|一定不一定是正数,a=0时不成立,故选项错误;
D、实数-a的绝对值不一定是a,a为负数时不成立,故选项错误.
故选B.
9.【答案】B
【解析】=|2a 1|=1 2a
∴2a-1≤0
∴a≤
故选B
10.【答案】A
【解析】解:∵二次根式 有意义,
∴2﹣x≥0,解得x≤2.
故选A.
11.【答案】 且x≠3
【解析】解:要使 在实数范围内有意义,必须
解得 且x≠3.
故答案为: 且x≠3
12.【答案】6
【解析】解:∵
∴
解得:
∴
∴
故答案为:6
13.【答案】2
【解析】解:∵ = ,
∴当n=2时, = =8,
∴n的最小值为2.
故填:2.
14.【答案】b﹣2a
【解析】解:观察数轴可知:a<0,b>0,
∴a﹣b<0,
则 +
故答案为:b﹣2a.
15.【答案】a≥﹣2且a≠﹣1
【解析】解:原式可化为: ,
∴ ,
解得a≥﹣2且a≠﹣1.
故答案为a≥﹣2且a≠﹣1.
16.【答案】解:由题意得: ,
解得:x=4,
则y=1,
+3y=2+3=5.
17.【答案】解:∵ =﹣a,
∴a≤0,
∴ ﹣|1﹣2a|
=﹣a+1﹣(1﹣2a)
=a
18.【答案】解:由数轴知:
∴,
∴
=-b-(a-b)-(c-a)-(-c)
=-b-a+b+a-c+c
=0
【答案】解:
∵y=﹣+8x,
∴2x﹣1=0,解得x=,
∴y=4,∴==4,
4的平方根是±2.
故的平方根是±2.
(2)∵﹣4<x<1,∴﹣2=|x+4|﹣2|x﹣1|=x+4+2(x﹣1)=x+4+2x﹣2=3x+2.
20.【答案】解:∵x2﹣12x+ +36=0,
∴x2﹣12x+36+ =0,
∴(x﹣6)2+ =0,
∴x﹣6=0,y+4=0,
解得:x=6,y=﹣4,
∴
21世纪教育网(www.21cnjy.com)
16.1二次根式的概念和性质(练习巩固)
一、单选题
1.下列各式中,正确的是( )
A. . B. C. D.
2.代数式 中x的取值范围在数轴上表示为( )
A. B.
C. D.
3.下列各式中,不是二次根式的是( )
A. B.﹣ C. D.
4.k、m、n为三整数,若 =k , =15 , =6 ,则下列有关于k、m、n的大小关系,何者正确?( )
A.k<m=n B.m=n<k C.m<n<k D.m<k<n
5.若(m-1)2+ =0,则m+n的值是( )
A.-1 B.0 C.1 D.2
6.如果 ,那么( )
A.a<3 B.a≤3 C.a>3 D.a≥3
7.若a、b为实数,且 ,则直线 不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.下列说法中正确的是( )
A.实数-a2是负数 B.=|a|
C.|-a|一定是正数 D.实数-a的绝对值是a
9.如果=1-2a,则( )
A.a< B.a≤ C.a> D.a≥
10.要使二次根式 有意义,字母x必须满足的条件是( )
A.x≤2 B.x<2 C.x≤﹣2 D.x<﹣2
二、填空题
11.使代数式 有意义的x的取值范围是 .
12.已知则ab= .
13. 是整数,则正整数n的最小值是 .
14.a、b为实数,在数轴上的位置如图所示,则 + 的值是 .
15.若代数式 有意义,则a的取值范围是 .
三、解答题
16.若x,y都是实数,且y=++1,求+3y的值.
17.已知 =﹣a,求 ﹣|1﹣2a|的值.
18.已知数a,b,c在数轴上的位置如图所示:
化简:
19.(1)已知y=﹣+8x,求的平方根.
(2)当﹣4<x<1时,化简﹣2.
20.已知实数x、y满足x2﹣12x+ +36=0,求 的值.
参考答案
1.【答案】A
【解析】解:A、 ,故此选项符合题意;
B、 ,无意义,故此选项不符合题意;
C、 ,故此选项不符合题意;
D、 ,故此选项不符合题意;
故答案为:A.
2.【答案】A
【解析】由题意,得:3﹣x≥0且x﹣1≠0,解得:x≤3且x≠1,在数轴上表示如图:
.
故答案为:A.
3.【答案】A
【解析】解:A、 ,不是二次根式;
B、﹣ ,是二次根式;
C、 ,是二次根式;
D、 ,是二次根式;
故选:A.
4.【答案】D
【解析】解: =3 , =15 , =6 ,
可得:k=3,m=2,n=5,
则m<k<n.
故选:D
5.【答案】A
【解析】∵(m-1)2+ =0
∴m 1=0,n+2=0;
∴m=1,n= 2,
∴m+n=1+( 2)= 1
故答案为:A.
6.【答案】B
【解析】解:∵ ,
∴3-a≥0,
∴a≤3,
故答案为:B.
7.【答案】C
【解析】解: 、 为实数,且 ,
,
解得, ,
,
,
直线 可以写成 ,
直线 经过第一、二、四象限,不经过第三象限,
直线 不经过的象限是第三象限,
故答案为:C.
8.【答案】B
【解析】A、实数-a2是负数,a=0时不成立,故选项错误;
B、=|a|,符合二次根式的意义,故选项正确,
C、|-a|一定不一定是正数,a=0时不成立,故选项错误;
D、实数-a的绝对值不一定是a,a为负数时不成立,故选项错误.
故选B.
9.【答案】B
【解析】=|2a 1|=1 2a
∴2a-1≤0
∴a≤
故选B
10.【答案】A
【解析】解:∵二次根式 有意义,
∴2﹣x≥0,解得x≤2.
故选A.
11.【答案】 且x≠3
【解析】解:要使 在实数范围内有意义,必须
解得 且x≠3.
故答案为: 且x≠3
12.【答案】6
【解析】解:∵
∴
解得:
∴
∴
故答案为:6
13.【答案】2
【解析】解:∵ = ,
∴当n=2时, = =8,
∴n的最小值为2.
故填:2.
14.【答案】b﹣2a
【解析】解:观察数轴可知:a<0,b>0,
∴a﹣b<0,
则 +
故答案为:b﹣2a.
15.【答案】a≥﹣2且a≠﹣1
【解析】解:原式可化为: ,
∴ ,
解得a≥﹣2且a≠﹣1.
故答案为a≥﹣2且a≠﹣1.
16.【答案】解:由题意得: ,
解得:x=4,
则y=1,
+3y=2+3=5.
17.【答案】解:∵ =﹣a,
∴a≤0,
∴ ﹣|1﹣2a|
=﹣a+1﹣(1﹣2a)
=a
18.【答案】解:由数轴知:
∴,
∴
=-b-(a-b)-(c-a)-(-c)
=-b-a+b+a-c+c
=0
【答案】解:
∵y=﹣+8x,
∴2x﹣1=0,解得x=,
∴y=4,∴==4,
4的平方根是±2.
故的平方根是±2.
(2)∵﹣4<x<1,∴﹣2=|x+4|﹣2|x﹣1|=x+4+2(x﹣1)=x+4+2x﹣2=3x+2.
20.【答案】解:∵x2﹣12x+ +36=0,
∴x2﹣12x+36+ =0,
∴(x﹣6)2+ =0,
∴x﹣6=0,y+4=0,
解得:x=6,y=﹣4,
∴
21世纪教育网(www.21cnjy.com)
