3.4.2 工程问题 课件(共19张PPT)
文档属性
| 名称 | 3.4.2 工程问题 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 832.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 16:26:35 | ||
图片预览





文档简介
(共19张PPT)
第2课时
3.4 实际问题与一元一次方程
知识回顾
用一元一次方程解决实际问题的基本过程:
审
设
列
解
验
答
1. 理解工程问题的背景,分清有关数量关系,能正确找出作为列方程依据的主要等量关系.
2. 进一步掌握用一元一次方程解决实际问题的基本过程.
学习目标
一项工作甲单独做 a 天完成,乙单独做 b 天完成,那么甲每天的工作效率是 ,乙每天的工作效率是 ,两人合作3天完成的工作量是 ,此时剩余的工作量是 .
课堂导入
例1 整理一批图书,由一个人做要 40 h 完成. 现计划由一部分人先做 4 h,然后增加 2人与他们一起做8 h,完成这项工作. 假设这些人的工作效率相同,具体应先安排多少人工作?
知识点 工程问题
新知探究
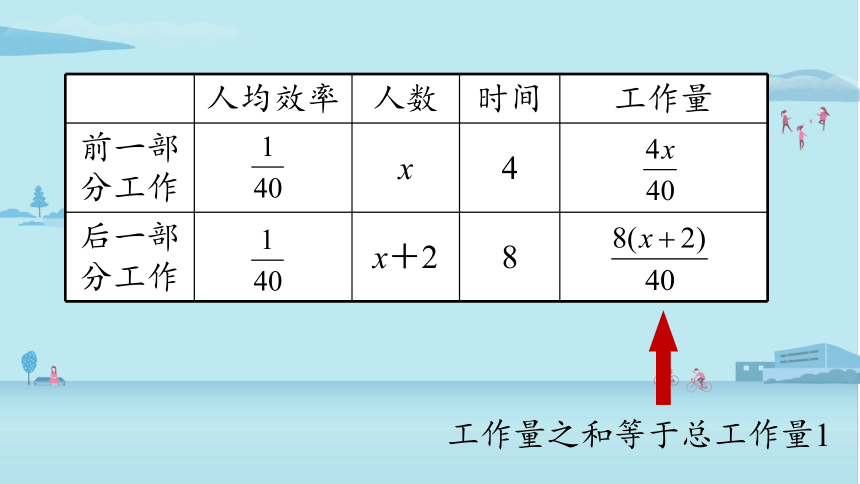
这类问题常常把总工作量看作1,并利用“工作量=人均效率×人数×时间”
人均效率 人数 时间 工作量
前一部分工作 x 4
后一部分工作 x+2 8
工作量之和等于总工作量1
解:设先安排 x 人做4 h,
根据前部分工作量+后部分工作量=总工作量1,
可列方程 .
解方程,得4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2.
答:应先安排 2人做4 小时.
工程问题中的基本量:工作量、工作效率、工作时间.
工程问题中的基本数量关系:
工作量=工作效率×工作时间;
合作的效率=各单独做的效率和;
总工作量=各部分工作量之和.
1. 我们常把总工作量看作1,此时工作效率可以用工作时间的倒数来表示,即工作效率 .
2. 多人合作时,合作效率=多人效率之和.
3. 有时会利用“工作量=人均效率×时间×人数”的关系列方程.
例2 加工某种工件,甲单独做要20天完成,乙只要10天就能完成任务,现在要求二人在12天内完成任务.
(1)乙需工作几天后甲再继续加工才可以正好按期完成任务?
(2)若要求二人在8天内完成任务,乙先加工几天后,甲加入合作加工,恰好能如期完成任务?
解:(1)设乙需工作x天后甲再继续加工才可正好按期完成任务,则甲做了(12-x)天.
依题意,得 ,
解得 x=8.
答:乙需工作8天后甲再继续加工才可以正好按期完成任务.
(2)设甲加工y天,两人如期完成任务,
则在甲加入之前,乙先工作了(8- y)天.
依题意,得 ,
解得 y =4,则 8- y =4.
答:乙先加工4天后,甲加入合作加工才可正好按期完成任务.
为了保证机场按时通航,通往机场的高速公路需要及时翻修完工,已知甲队单独做需要10天完成,乙队单独做需要15天完成,若甲、乙两队合作5天后,再由乙队单独完成剩余的工作量,共需要多少天?
跟踪训练
新知探究
根据甲完成的工作量+乙完成的工作量=总工作量,可列方程
解:设共需 x 天.
根据甲、乙两队合作5天完成的工作量+乙队单独完成剩余的工作量=总工作量,
列出方程 ,
解得 x=7.5.
答:若甲、乙两队合作5天后,再由乙队单独完成剩余的工作量,共需要7.5天.
1.某市为打造引江枢纽风光带,将一段长为 1.2千米的河道整治任务交由甲、乙两个工程队接力完成,共用时60天. 已知甲队每天整治24米,乙队每天整治16米. 求甲、乙两队分别整治河道多少米.
随堂练习
甲队整治河道的长度+乙队整治河道的长度=1200;
甲队工作的天数+乙队工作的天数=60
解:设甲队整治河道 x 米,则乙队整治河道(1200-x)米.
根据题意列方程,得 ,
解方程,得 2x+3(1200-x)=2880,
2x+3600-3x=2880,
x=720.
1200-x=480.
答:甲队整治河道720米,乙队整治河道480米.
2.检查一处住宅区的自来水管,甲单独完成需14天,乙单独完成需18天,丙单独完成需12天,前7天由甲、乙两人合作,但乙中途离开了一段时间,后2天由乙、丙两人合作完成,则乙中途离开了几天?
甲7天完成的工作量+乙(7-x)天完成的工作量+乙、丙合作2天完成的工作量=1(设乙中途离开了x天)
解:设乙中途离开了 x 天.
根据题意,得 ,
即 ,
去分母,得 9+(7-x)+2+3=18,
解得 x=3.
答:乙中途离开了3天.
工程问题中的基本量:
工作量、工作效率、工作时间.
工程问题中的基本数量关系:
工作量=工作效率×工作时间;
合作的效率=各单独做的效率和;
总工作量=各部分工作量之和.
课堂小结
第2课时
3.4 实际问题与一元一次方程
知识回顾
用一元一次方程解决实际问题的基本过程:
审
设
列
解
验
答
1. 理解工程问题的背景,分清有关数量关系,能正确找出作为列方程依据的主要等量关系.
2. 进一步掌握用一元一次方程解决实际问题的基本过程.
学习目标
一项工作甲单独做 a 天完成,乙单独做 b 天完成,那么甲每天的工作效率是 ,乙每天的工作效率是 ,两人合作3天完成的工作量是 ,此时剩余的工作量是 .
课堂导入
例1 整理一批图书,由一个人做要 40 h 完成. 现计划由一部分人先做 4 h,然后增加 2人与他们一起做8 h,完成这项工作. 假设这些人的工作效率相同,具体应先安排多少人工作?
知识点 工程问题
新知探究
这类问题常常把总工作量看作1,并利用“工作量=人均效率×人数×时间”
人均效率 人数 时间 工作量
前一部分工作 x 4
后一部分工作 x+2 8
工作量之和等于总工作量1
解:设先安排 x 人做4 h,
根据前部分工作量+后部分工作量=总工作量1,
可列方程 .
解方程,得4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2.
答:应先安排 2人做4 小时.
工程问题中的基本量:工作量、工作效率、工作时间.
工程问题中的基本数量关系:
工作量=工作效率×工作时间;
合作的效率=各单独做的效率和;
总工作量=各部分工作量之和.
1. 我们常把总工作量看作1,此时工作效率可以用工作时间的倒数来表示,即工作效率 .
2. 多人合作时,合作效率=多人效率之和.
3. 有时会利用“工作量=人均效率×时间×人数”的关系列方程.
例2 加工某种工件,甲单独做要20天完成,乙只要10天就能完成任务,现在要求二人在12天内完成任务.
(1)乙需工作几天后甲再继续加工才可以正好按期完成任务?
(2)若要求二人在8天内完成任务,乙先加工几天后,甲加入合作加工,恰好能如期完成任务?
解:(1)设乙需工作x天后甲再继续加工才可正好按期完成任务,则甲做了(12-x)天.
依题意,得 ,
解得 x=8.
答:乙需工作8天后甲再继续加工才可以正好按期完成任务.
(2)设甲加工y天,两人如期完成任务,
则在甲加入之前,乙先工作了(8- y)天.
依题意,得 ,
解得 y =4,则 8- y =4.
答:乙先加工4天后,甲加入合作加工才可正好按期完成任务.
为了保证机场按时通航,通往机场的高速公路需要及时翻修完工,已知甲队单独做需要10天完成,乙队单独做需要15天完成,若甲、乙两队合作5天后,再由乙队单独完成剩余的工作量,共需要多少天?
跟踪训练
新知探究
根据甲完成的工作量+乙完成的工作量=总工作量,可列方程
解:设共需 x 天.
根据甲、乙两队合作5天完成的工作量+乙队单独完成剩余的工作量=总工作量,
列出方程 ,
解得 x=7.5.
答:若甲、乙两队合作5天后,再由乙队单独完成剩余的工作量,共需要7.5天.
1.某市为打造引江枢纽风光带,将一段长为 1.2千米的河道整治任务交由甲、乙两个工程队接力完成,共用时60天. 已知甲队每天整治24米,乙队每天整治16米. 求甲、乙两队分别整治河道多少米.
随堂练习
甲队整治河道的长度+乙队整治河道的长度=1200;
甲队工作的天数+乙队工作的天数=60
解:设甲队整治河道 x 米,则乙队整治河道(1200-x)米.
根据题意列方程,得 ,
解方程,得 2x+3(1200-x)=2880,
2x+3600-3x=2880,
x=720.
1200-x=480.
答:甲队整治河道720米,乙队整治河道480米.
2.检查一处住宅区的自来水管,甲单独完成需14天,乙单独完成需18天,丙单独完成需12天,前7天由甲、乙两人合作,但乙中途离开了一段时间,后2天由乙、丙两人合作完成,则乙中途离开了几天?
甲7天完成的工作量+乙(7-x)天完成的工作量+乙、丙合作2天完成的工作量=1(设乙中途离开了x天)
解:设乙中途离开了 x 天.
根据题意,得 ,
即 ,
去分母,得 9+(7-x)+2+3=18,
解得 x=3.
答:乙中途离开了3天.
工程问题中的基本量:
工作量、工作效率、工作时间.
工程问题中的基本数量关系:
工作量=工作效率×工作时间;
合作的效率=各单独做的效率和;
总工作量=各部分工作量之和.
课堂小结
