15.1.1 从分数到分式课件(共29张PPT)
文档属性
| 名称 | 15.1.1 从分数到分式课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 19:14:59 | ||
图片预览






文档简介
(共29张PPT)
从分数到分式
几个数或字母的积的式子是单项式,
整式包括单项式和多项式.
几个单项式的和是多项式.
整式包括什么?你能说明它们的特点吗?
思考
单独的一个数或一个字母也是单项式.
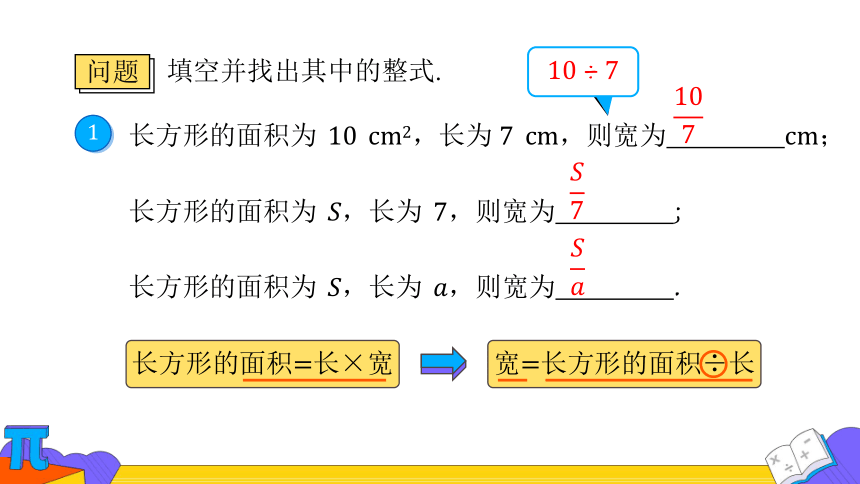
填空并找出其中的整式.
长方形的面积为 ,长为 ,则宽为 ;
长方形的面积为 ,长为 ,则宽为 ;
长方形的面积为 ,长为 ,则宽为 .
长方形的面积长宽
宽长方形的面积长
1
问题
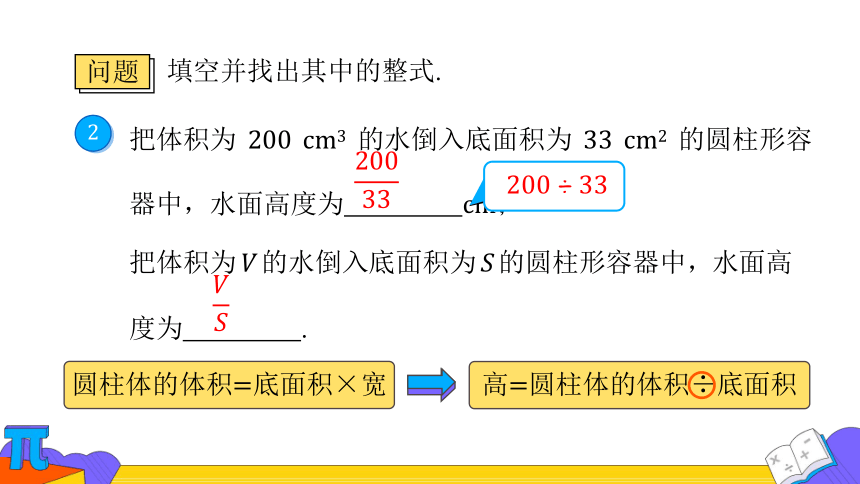
把体积为 的水倒入底面积为 的圆柱形容
器中,水面高度为 ;
把体积为的水倒入底面积为的圆柱形容器中,水面高
度为 .
圆柱体的体积底面积宽
高圆柱体的体积底面积
2
填空并找出其中的整式.
问题
请观察得到的式子,你能找出其中的整式吗?
,
,
,
,
那么 , 和上面三个整式相比有什么不同呢?
思考
.
整式:
,
,
.
归纳
一般地,如果 表示两个整式,并且 中
含有字母,那么式子 叫做分式.
在分式 中, 叫做分子, 叫做分母.
;
;
;
;
;
.
1
2
3
4
5
6
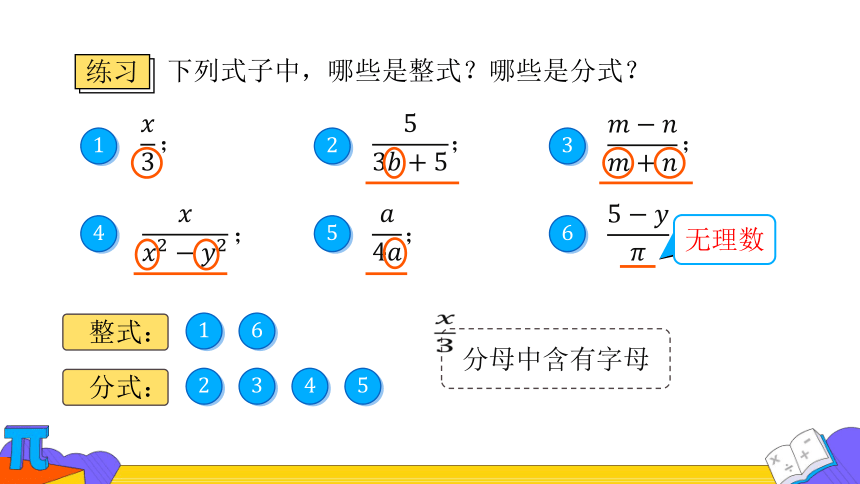
整式:
分式:
1
6
4
2
3
5
分母中含有字母
无理数
下列式子中,哪些是整式?哪些是分式?
练习
探究新知
分式是除法的表示形式,那么我们也可以利用除法来研究分式.
你还记得除法的相关知识吗?
回忆
不能作除数;
1
除以任何一个不等于 的数,都得 ;
2
两数相除,同号得正,异号得负,并把绝对值相除.
3
探究新知
类比分数有意义,我们可以得到当分式的分母不等于 时,
分式有意义.
不能作除数.
1
即 当 时,分式 才有意义.
解:
1
要使分式 有意义,则分母 ,
即 ;
下列分式中的字母满足什么条件时分式有意义?
例
1
2
3
;
;
;
即 ;
2
要使分式 有意义,则分母 ,
3
要使分式 有意义,则分母 ,
即 ;
;
下列分式中的字母满足什么条件时分式有意义?
4
5
;
;
解:
即 ;
4
要使分式 有意义,则分母 ,
即 且 ;
5
要使分式 有意义,则分母 ,
且 ,
例
下列分式中的字母满足什么条件时分式有意义?
6
解:
6
不论 取何值,分母 恒成立,
.
所以 取任意实数,分式 都有意义.
例
下列分式中的字母满足什么条件时分式有意义?
1
2
3
;
;
;
4
.
解:
1
要使分式 有意义,则分母 ;
2
要使分式 有意义,则分母 ,
即 ;
练习
下列分式中的字母满足什么条件时分式有意义?
1
2
3
4
解:
3
要使分式 有意义,则分母 ,
即 ;
4
要使分式 有意义,则分母 ,
即 且 .
练习
;
;
;
.
所以当 时,
.
探究新知
那么分式有没有值为的情况呢?如果分式的值为,分式字母取值有什么要求呢?
除以任何一个不等于 的数,都得 .
2
分式 中 是被除数, 是除数,
当 为何值时,分式的值为 0?
1
2
3
;
;
.
解:
1
要使分式 的值为 ,
则分子 ,分母 ,
且 ,
.
例
当 为何值时,分式的值为 0?
1
2
3
;
;
.
解:
2
要使分式 的值为 ,
则分子 ,分母 ,
且 ,
.
例
当 为何值时,分式的值为 0?
1
2
3
;
;
.
解:
3
要使分式 的值为 ,
则分子 ,分母 ,
, 且 ,
.
例
在什么条件下,下列分式的值为 ?
1
2
3
;
;
.
解:
1
要使分式 值为 ,则分子 ,分母 ,
且 ,
所以 ;
练习
在什么条件下,下列分式的值为 ?
1
2
3
;
;
.
2
要使分式 值为 ,则分子 ,分母 ,
且 ,
所以 ;
解:
练习
在什么条件下,下列分式的值为 ?
1
2
3
;
;
.
或 ,
所以 .
3
要使分式 值为 ,则分子 ,
或
分母 ,
且 ,
解:
练习
如果分式 的值为正数,那么 同为正数或负数;
探究新知
两数相除,同号得正,异号得负,并把绝对值相除.
3
如果分式 的值为负数,那么 为一正一负.
当 满足什么条件时,下列分式的值为正数?
1
2
;
.
解:
1
根据除法法则,若分式 的值为正数,则 与 的
符号相同,
例
所以 ;
2
根据除法法则,若分式 的值为正数,则 与
的符号相同,
解:
所以 .
1
2
;
.
,
思考
如果分式 的值为负数呢?
所以 .
,
例
当 满足什么条件时,下列分式的值为正数?
已知分式 ,
1
当 满足什么条件时,该分式有意义?
当 满足什么条件时,该分式的值大于零?
2
分母
解:
1
要使分式 有意义,则分母 ,
所以 ;
正
2
要使分式 的值大于 ,则 与 同号,
,
所以 .
练习
课
堂
小
结
1
分式的概念:一般地,如果 表示两个整式,
并且 中含有字母,那么式子 叫做分式. 在分
式 中, 叫做分子, 叫做分母.
课
堂
小
结
分式有意义,就是要分母不为 .
2
分式的值为 必须满足两个条件:
3
分子的值为 ;
分母的值不等于 .
分式的学习类比分数,从除法的角度考虑.
4
作业
甲每小时做 个零件,做 个零件所用的时间,可用式子表示成 小时.
公顷麦田共收小麦 吨,平均每公顷的产量可用式子表示成 吨.
轮船在静水中每小时走 千米,水流速度是 千米/时,轮船在逆流中航行 千米
所需要的时间可用式子表示成 小时.
式子 , , 中 ,是分式的有( ).
使得分式 有意义的 的取值范围是( ).
使分式 值为 的 值是( ).
若分式 的值是负数,则 满足( ).
1
2
3
4
5
6
7
再 见
从分数到分式
几个数或字母的积的式子是单项式,
整式包括单项式和多项式.
几个单项式的和是多项式.
整式包括什么?你能说明它们的特点吗?
思考
单独的一个数或一个字母也是单项式.
填空并找出其中的整式.
长方形的面积为 ,长为 ,则宽为 ;
长方形的面积为 ,长为 ,则宽为 ;
长方形的面积为 ,长为 ,则宽为 .
长方形的面积长宽
宽长方形的面积长
1
问题
把体积为 的水倒入底面积为 的圆柱形容
器中,水面高度为 ;
把体积为的水倒入底面积为的圆柱形容器中,水面高
度为 .
圆柱体的体积底面积宽
高圆柱体的体积底面积
2
填空并找出其中的整式.
问题
请观察得到的式子,你能找出其中的整式吗?
,
,
,
,
那么 , 和上面三个整式相比有什么不同呢?
思考
.
整式:
,
,
.
归纳
一般地,如果 表示两个整式,并且 中
含有字母,那么式子 叫做分式.
在分式 中, 叫做分子, 叫做分母.
;
;
;
;
;
.
1
2
3
4
5
6
整式:
分式:
1
6
4
2
3
5
分母中含有字母
无理数
下列式子中,哪些是整式?哪些是分式?
练习
探究新知
分式是除法的表示形式,那么我们也可以利用除法来研究分式.
你还记得除法的相关知识吗?
回忆
不能作除数;
1
除以任何一个不等于 的数,都得 ;
2
两数相除,同号得正,异号得负,并把绝对值相除.
3
探究新知
类比分数有意义,我们可以得到当分式的分母不等于 时,
分式有意义.
不能作除数.
1
即 当 时,分式 才有意义.
解:
1
要使分式 有意义,则分母 ,
即 ;
下列分式中的字母满足什么条件时分式有意义?
例
1
2
3
;
;
;
即 ;
2
要使分式 有意义,则分母 ,
3
要使分式 有意义,则分母 ,
即 ;
;
下列分式中的字母满足什么条件时分式有意义?
4
5
;
;
解:
即 ;
4
要使分式 有意义,则分母 ,
即 且 ;
5
要使分式 有意义,则分母 ,
且 ,
例
下列分式中的字母满足什么条件时分式有意义?
6
解:
6
不论 取何值,分母 恒成立,
.
所以 取任意实数,分式 都有意义.
例
下列分式中的字母满足什么条件时分式有意义?
1
2
3
;
;
;
4
.
解:
1
要使分式 有意义,则分母 ;
2
要使分式 有意义,则分母 ,
即 ;
练习
下列分式中的字母满足什么条件时分式有意义?
1
2
3
4
解:
3
要使分式 有意义,则分母 ,
即 ;
4
要使分式 有意义,则分母 ,
即 且 .
练习
;
;
;
.
所以当 时,
.
探究新知
那么分式有没有值为的情况呢?如果分式的值为,分式字母取值有什么要求呢?
除以任何一个不等于 的数,都得 .
2
分式 中 是被除数, 是除数,
当 为何值时,分式的值为 0?
1
2
3
;
;
.
解:
1
要使分式 的值为 ,
则分子 ,分母 ,
且 ,
.
例
当 为何值时,分式的值为 0?
1
2
3
;
;
.
解:
2
要使分式 的值为 ,
则分子 ,分母 ,
且 ,
.
例
当 为何值时,分式的值为 0?
1
2
3
;
;
.
解:
3
要使分式 的值为 ,
则分子 ,分母 ,
, 且 ,
.
例
在什么条件下,下列分式的值为 ?
1
2
3
;
;
.
解:
1
要使分式 值为 ,则分子 ,分母 ,
且 ,
所以 ;
练习
在什么条件下,下列分式的值为 ?
1
2
3
;
;
.
2
要使分式 值为 ,则分子 ,分母 ,
且 ,
所以 ;
解:
练习
在什么条件下,下列分式的值为 ?
1
2
3
;
;
.
或 ,
所以 .
3
要使分式 值为 ,则分子 ,
或
分母 ,
且 ,
解:
练习
如果分式 的值为正数,那么 同为正数或负数;
探究新知
两数相除,同号得正,异号得负,并把绝对值相除.
3
如果分式 的值为负数,那么 为一正一负.
当 满足什么条件时,下列分式的值为正数?
1
2
;
.
解:
1
根据除法法则,若分式 的值为正数,则 与 的
符号相同,
例
所以 ;
2
根据除法法则,若分式 的值为正数,则 与
的符号相同,
解:
所以 .
1
2
;
.
,
思考
如果分式 的值为负数呢?
所以 .
,
例
当 满足什么条件时,下列分式的值为正数?
已知分式 ,
1
当 满足什么条件时,该分式有意义?
当 满足什么条件时,该分式的值大于零?
2
分母
解:
1
要使分式 有意义,则分母 ,
所以 ;
正
2
要使分式 的值大于 ,则 与 同号,
,
所以 .
练习
课
堂
小
结
1
分式的概念:一般地,如果 表示两个整式,
并且 中含有字母,那么式子 叫做分式. 在分
式 中, 叫做分子, 叫做分母.
课
堂
小
结
分式有意义,就是要分母不为 .
2
分式的值为 必须满足两个条件:
3
分子的值为 ;
分母的值不等于 .
分式的学习类比分数,从除法的角度考虑.
4
作业
甲每小时做 个零件,做 个零件所用的时间,可用式子表示成 小时.
公顷麦田共收小麦 吨,平均每公顷的产量可用式子表示成 吨.
轮船在静水中每小时走 千米,水流速度是 千米/时,轮船在逆流中航行 千米
所需要的时间可用式子表示成 小时.
式子 , , 中 ,是分式的有( ).
使得分式 有意义的 的取值范围是( ).
使分式 值为 的 值是( ).
若分式 的值是负数,则 满足( ).
1
2
3
4
5
6
7
再 见
