15.1.2 分式的基本性质 课件(共36张PPT)
文档属性
| 名称 | 15.1.2 分式的基本性质 课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 21:04:32 | ||
图片预览






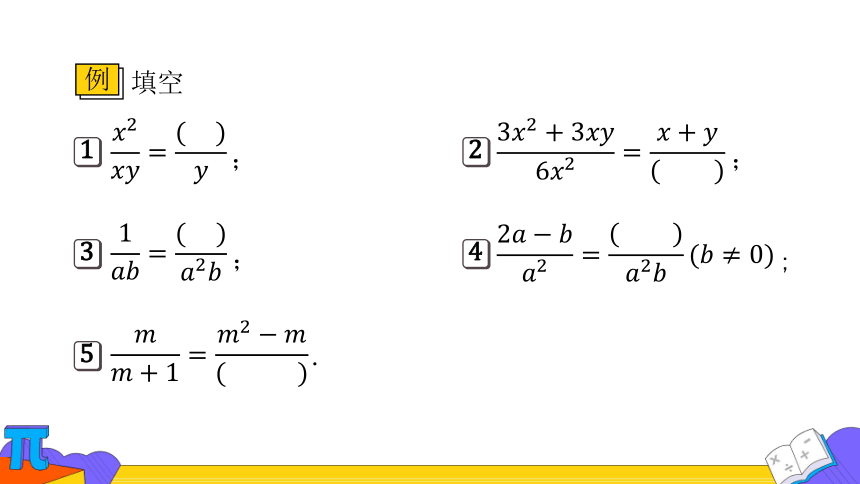



文档简介
(共36张PPT)
分式的基本性质
你能说出分式的概念吗?
一般地,如果,表示两个整式,并且中含有字母,那么式子叫做分式.
在分式中,叫做分子,叫做分母.
分式有意义时,分式中字母的取值范围.
你能叙述分数的基本性质吗?
一个分数的分子、分母乘(或除以)同一个不为的数,分数的值不变.,其中,
,其中, 数.
,
探究新知
类比分数的基本性质,你能猜想分式有什么性质吗?
分式的分子、分母乘以(或除以)同一个不是 的
数,分式的值不变.
探究新知
类比分数的基本性质,你能猜想分式有什么性质吗?
如图,三个完全相同的小长方形摆成一个大长方形,如果一个小长方形的面积为,长为,你能求出长方形的宽吗?
分式的分子、分母乘同一个不是的数,分式的值不变.
探究新知
类比分数的基本性质,你能猜想分式有什么性质吗?
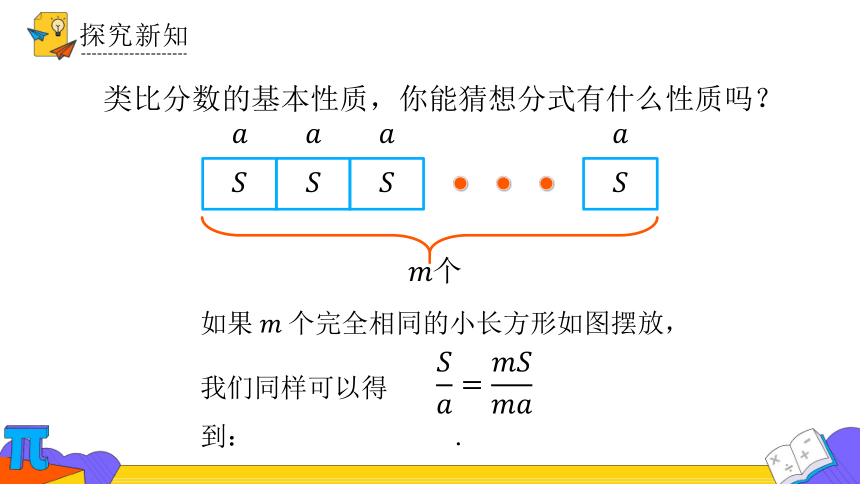
如果个完全相同的小长方形如图摆放,
我们同样可以得到: .
探究新知
类比分数的基本性质,你能猜想分式有什么性质吗?
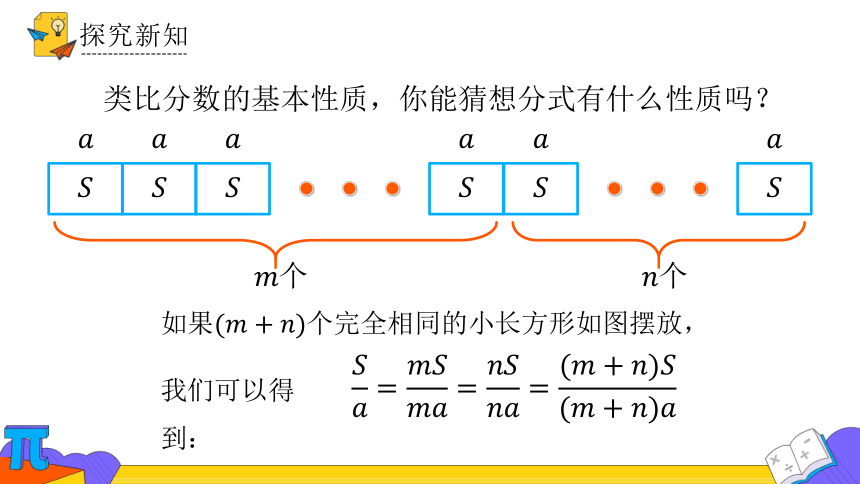
如果个完全相同的小长方形如图摆放,
我们可以得到: .
归纳
分式的分子、分母乘(或除以)同一个不等于的整式,分式的值不变.
分式的基本性质
即,
其中,是整式.
例
填空
1
3
5
2
4
.
;
例
1
解:
因为的分母除以才能化为,为了保证分式的值不变,根据分式的基本性质,分子也要除以.
即
例
2
解:
的分子,除以化为,所以分母也要除以,即
例
3
解:
的分母乘才能化为,根据分式的基本性质,分子也要乘. 即
例
4
解:
的分母乘化为,根据分式的基本性质,分子也要乘. 即
例
5
解:
的分子乘化为,根据分式的基本性质,分母也要乘,即
.
归纳
利用分式的基本性质对分式进行变形时要注意:
分子、分母进行相同的乘(除)运算;
1
分子(分母)是多项式时可以进行因式分解.
2
练习
填空
1
2
.
分子、分母除以
分子、分母乘
,
练习
下列各式中,正确的是( ).
.分子、分母减去,不符合分式的基本性质.
.分子、分母除以,结果为.
.分子、分母部分除以,不符合分式的基本性质.
分式的值,使分式的分子、分母中的字母系数都不含“”号.
例
解:
利用分式的性质,分子、分母都乘
1
2
.
3
;
;
.
分式的值,使分式的分子、分母中的字母系数都不含“”号.
例
1
2
.
3
;
;
解:
;
归纳
类比学习分数时符号的变化,利用分式的基本性质进行变形可得
分式本身及其分子、分母这三处的正负号中,同时改变两
处,分式的值不改变.
分式的变号法则
1
2
3
;
;
.
解:
1
2
3
不改变分式的值,使下列分式的分子、分母都不含负号.
练习
解:
1
2
3
;
不改变分式的值,使下列分式的分子、分母都不含负号.
练习
1
2
3
;
;
.
解:
1
2
3
;
;
不改变分式的值,使下列分式的分子、分母都不含负号.
练习
1
2
3
;
;
.
不改变分式的值,使下列分式的分子、分母都不含负号.
练习
解:
1
2
3
;
;
.
1
2
3
;
;
.
解:
,分子分母都除以得,所以分式的值不变;
1
把下列分式中的字母,同时扩大到原来的倍,分式的值会怎么变化?
例
1
2
;
.
1
2
.
解:
,分子分母都除以得,所以分式的值不变;
1
把下列分式中的字母,同时扩大到原来的倍,分式的值会怎么变化?
例
;
解:
,分子分母都除以得,所以分式的值不变;
2
把下列分式中的字母,同时扩大到原来的倍,分式的值会怎么变化?
例
1
2
;
.
解:
,分子分母都除以得,所以分式的值扩大到原来的倍;
2
把下列分式中的字母,同时扩大到原来的倍,分式的值会怎么变化?
例
1
2
;
.
解:
,分子分母都除以得,所以分式的值扩大到原来的倍.
2
把下列分式中的字母,同时扩大到原来的倍,分式的值会怎么变化?
例
1
2
;
.
练习
如果把分式中的和都扩大倍,那么分式的值( ).
A. 扩大倍
C. 是原来的
B. 缩小
D. 不变
练习
如果把分式中的和都扩大倍,那么分式的值( ).
A. 扩大倍
C. 是原来的
B. 缩小
D. 不变
分式的基本性质:
课
堂
小
结
1
应用分式的基本性质需要注意:
分子、分母应同时做乘、除法中的同一种运算;
所乘(或除以)的必须是同一个整式;
分式的分子与分母同乘(或除以)一个不等于的整式,分式的值不变.
1
2
3
所乘(或除以)的整式应该不等于.
课
堂
小
结
分式的学习类比分数的学习,可以借助图形来提升对于代数的理解.
3
分式本身及其分子、分母这三处的正负号中,同时改变两处,分式的值不改变.
分式的变号法则:
2
课后作业
写出等式中未知的分子或分母:
1
1
2
3
不改变分式的值,使分式的分子与分母都不含负号:
2
3
把分式中的和都扩大为原来的倍,那么这个分式的值( ).
A. 扩大为原来的倍
C. 缩小到原来的
B. 不变
D. 扩大为原来的倍
1
2
;
.
;
;
.
课后作业
不改变分式的值,使分式的分子、分母中的首项的系数都不含“”号:
4
1
2
不改变分式的值,把下列各式的分子与分母中各项的系数都化为整数:
5
1
2
.
;
;
.
再 见
分式的基本性质
你能说出分式的概念吗?
一般地,如果,表示两个整式,并且中含有字母,那么式子叫做分式.
在分式中,叫做分子,叫做分母.
分式有意义时,分式中字母的取值范围.
你能叙述分数的基本性质吗?
一个分数的分子、分母乘(或除以)同一个不为的数,分数的值不变.,其中,
,其中, 数.
,
探究新知
类比分数的基本性质,你能猜想分式有什么性质吗?
分式的分子、分母乘以(或除以)同一个不是 的
数,分式的值不变.
探究新知
类比分数的基本性质,你能猜想分式有什么性质吗?
如图,三个完全相同的小长方形摆成一个大长方形,如果一个小长方形的面积为,长为,你能求出长方形的宽吗?
分式的分子、分母乘同一个不是的数,分式的值不变.
探究新知
类比分数的基本性质,你能猜想分式有什么性质吗?
如果个完全相同的小长方形如图摆放,
我们同样可以得到: .
探究新知
类比分数的基本性质,你能猜想分式有什么性质吗?
如果个完全相同的小长方形如图摆放,
我们可以得到: .
归纳
分式的分子、分母乘(或除以)同一个不等于的整式,分式的值不变.
分式的基本性质
即,
其中,是整式.
例
填空
1
3
5
2
4
.
;
例
1
解:
因为的分母除以才能化为,为了保证分式的值不变,根据分式的基本性质,分子也要除以.
即
例
2
解:
的分子,除以化为,所以分母也要除以,即
例
3
解:
的分母乘才能化为,根据分式的基本性质,分子也要乘. 即
例
4
解:
的分母乘化为,根据分式的基本性质,分子也要乘. 即
例
5
解:
的分子乘化为,根据分式的基本性质,分母也要乘,即
.
归纳
利用分式的基本性质对分式进行变形时要注意:
分子、分母进行相同的乘(除)运算;
1
分子(分母)是多项式时可以进行因式分解.
2
练习
填空
1
2
.
分子、分母除以
分子、分母乘
,
练习
下列各式中,正确的是( ).
.分子、分母减去,不符合分式的基本性质.
.分子、分母除以,结果为.
.分子、分母部分除以,不符合分式的基本性质.
分式的值,使分式的分子、分母中的字母系数都不含“”号.
例
解:
利用分式的性质,分子、分母都乘
1
2
.
3
;
;
.
分式的值,使分式的分子、分母中的字母系数都不含“”号.
例
1
2
.
3
;
;
解:
;
归纳
类比学习分数时符号的变化,利用分式的基本性质进行变形可得
分式本身及其分子、分母这三处的正负号中,同时改变两
处,分式的值不改变.
分式的变号法则
1
2
3
;
;
.
解:
1
2
3
不改变分式的值,使下列分式的分子、分母都不含负号.
练习
解:
1
2
3
;
不改变分式的值,使下列分式的分子、分母都不含负号.
练习
1
2
3
;
;
.
解:
1
2
3
;
;
不改变分式的值,使下列分式的分子、分母都不含负号.
练习
1
2
3
;
;
.
不改变分式的值,使下列分式的分子、分母都不含负号.
练习
解:
1
2
3
;
;
.
1
2
3
;
;
.
解:
,分子分母都除以得,所以分式的值不变;
1
把下列分式中的字母,同时扩大到原来的倍,分式的值会怎么变化?
例
1
2
;
.
1
2
.
解:
,分子分母都除以得,所以分式的值不变;
1
把下列分式中的字母,同时扩大到原来的倍,分式的值会怎么变化?
例
;
解:
,分子分母都除以得,所以分式的值不变;
2
把下列分式中的字母,同时扩大到原来的倍,分式的值会怎么变化?
例
1
2
;
.
解:
,分子分母都除以得,所以分式的值扩大到原来的倍;
2
把下列分式中的字母,同时扩大到原来的倍,分式的值会怎么变化?
例
1
2
;
.
解:
,分子分母都除以得,所以分式的值扩大到原来的倍.
2
把下列分式中的字母,同时扩大到原来的倍,分式的值会怎么变化?
例
1
2
;
.
练习
如果把分式中的和都扩大倍,那么分式的值( ).
A. 扩大倍
C. 是原来的
B. 缩小
D. 不变
练习
如果把分式中的和都扩大倍,那么分式的值( ).
A. 扩大倍
C. 是原来的
B. 缩小
D. 不变
分式的基本性质:
课
堂
小
结
1
应用分式的基本性质需要注意:
分子、分母应同时做乘、除法中的同一种运算;
所乘(或除以)的必须是同一个整式;
分式的分子与分母同乘(或除以)一个不等于的整式,分式的值不变.
1
2
3
所乘(或除以)的整式应该不等于.
课
堂
小
结
分式的学习类比分数的学习,可以借助图形来提升对于代数的理解.
3
分式本身及其分子、分母这三处的正负号中,同时改变两处,分式的值不改变.
分式的变号法则:
2
课后作业
写出等式中未知的分子或分母:
1
1
2
3
不改变分式的值,使分式的分子与分母都不含负号:
2
3
把分式中的和都扩大为原来的倍,那么这个分式的值( ).
A. 扩大为原来的倍
C. 缩小到原来的
B. 不变
D. 扩大为原来的倍
1
2
;
.
;
;
.
课后作业
不改变分式的值,使分式的分子、分母中的首项的系数都不含“”号:
4
1
2
不改变分式的值,把下列各式的分子与分母中各项的系数都化为整数:
5
1
2
.
;
;
.
再 见
