15.3.1 分式方程 课件(共26张PPT)
文档属性
| 名称 | 15.3.1 分式方程 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 20:57:42 | ||
图片预览





文档简介
(共26张PPT)
分式方程
(第一课时)
情景引入
分析
,
顺
静
水流
.
逆
静
水流
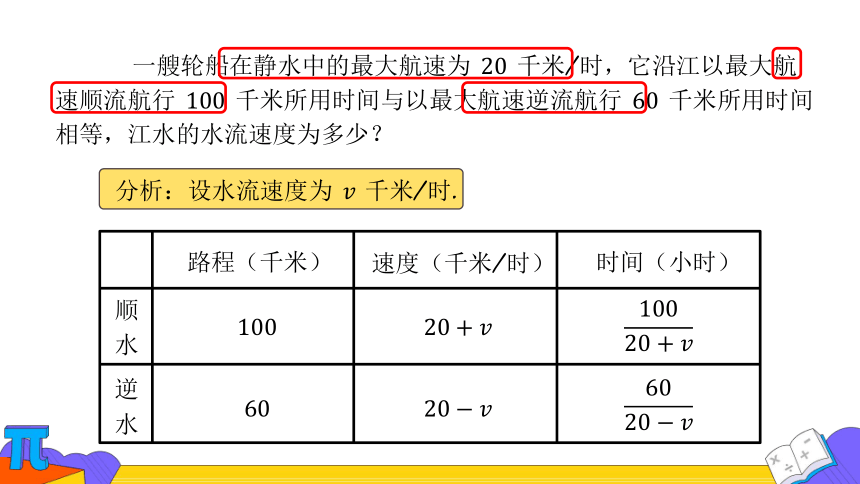
一艘轮船在静水中的最大航速为 千米/时,它沿江以最大航速顺流航行 千米所用时间与以最大航速逆流航行 千米所用时间相等,江水的水流速度为多少?
一艘轮船在静水中的最大航速为 千米/时,它沿江以最大航速顺流航行 千米所用时间与以最大航速逆流航行 千米所用时间相等,江水的水流速度为多少?
路程(千米)
速度(千米/时)
时间(小时)
顺水
逆水
分析:设水流速度为 千米/时.
路程(千米)
速度(千米/时)
时间(小时)
顺水
逆水
所用时间相等
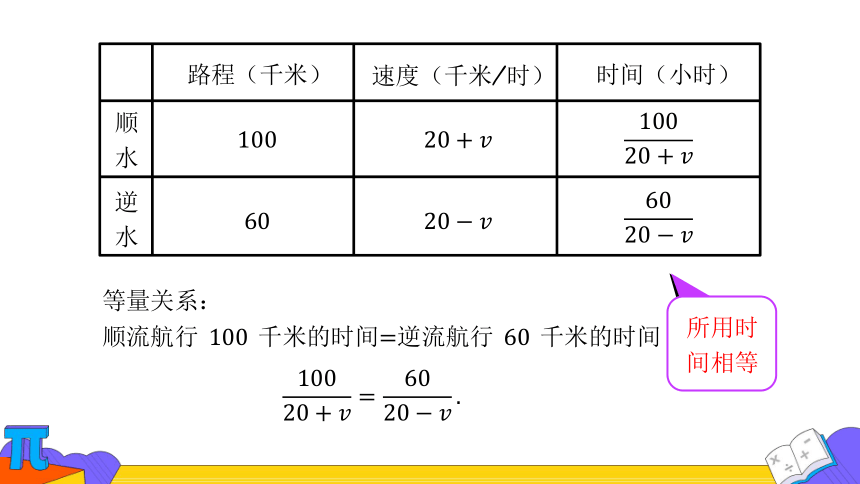
等量关系:
顺流航行 千米的时间逆流航行 千米的时间
温故知新
方程:含有未知数的等式叫方程.
一元一次方程
二元一次方程
含有一个未知数,且未知数项的次数为一的整式方程.
含有两个未知数,且含有未知数的项的次数为一的整式方程.
整式方程
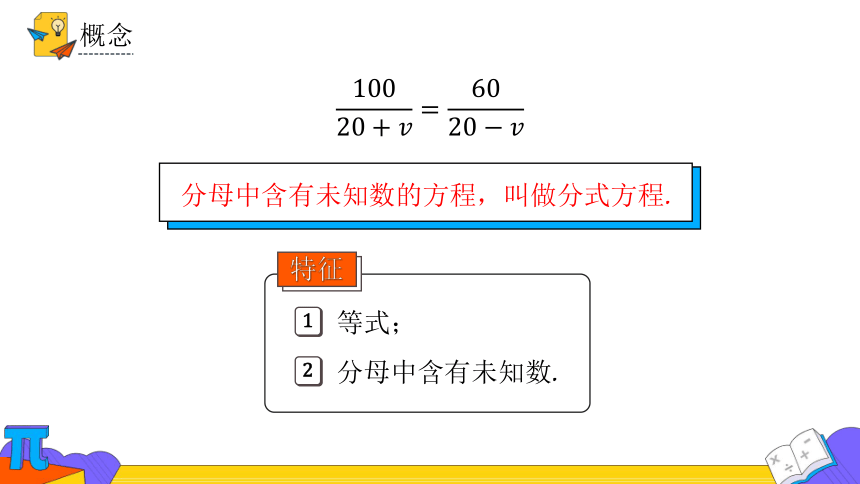
概念
分母中含有未知数的方程,叫做分式方程.
特征
1
等式;
2
分母中含有未知数.
巩固定义
下列关于 的方程中哪些是分式方程?为什么?
例
1
2
3
5
4
6
解方程
例
去分母,得 .
去括号,得 .
解:
移项,得
合并同类项,得
系数化为 ,得
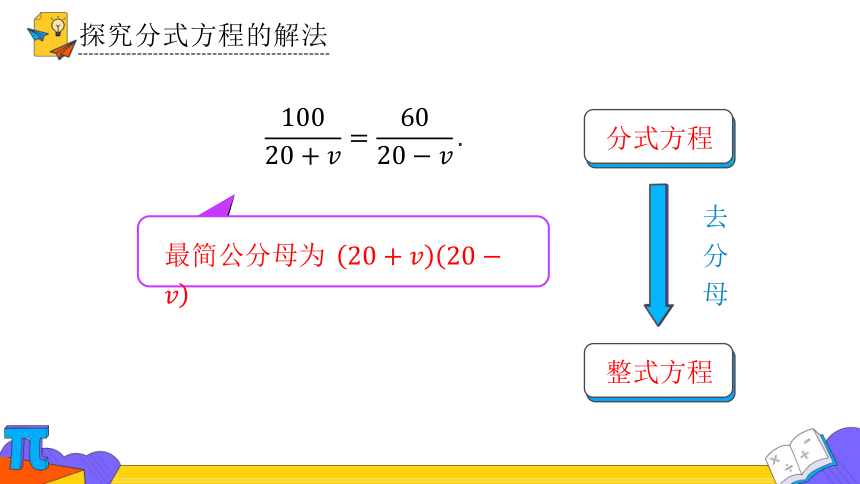
探究分式方程的解法
整式方程
分式方程
去分母
最简公分母为
.
去分母,两边同乘
.
去括号
.
移项
.
合并同类项
.
系数化为
解得 .
是原分式方程的解吗?
将 代入原方程,发现左边右边.
是原分式方程的解.
整式方程
分式方程
去分母
最简公分母为
.
去分母,两边同乘
.
移项
.
合并同类项
解得 .
是原分式方程的解吗?
当 时,左边和右边分式的分母都为 ,分式无意义.
不是原分式方程的解.
.
同乘
.
去括号
.
移项
.
合并同类项
.
系数化为
去分母
.
同乘
.
移项
.
合并同类项
去分母
.
同乘
去分母
.
同乘
去分母
解得 .
解得 .
检验是解分式方程的必要步骤
如何更简便地检验呢?
将整式方程的解代入最简公分母,如果最简公分母的值不为 ,则整式方程的解是原分式方程的解;如果最简公分母的值为 ,这个解不是原分式方程的解.
解下列分式方程:
例
1
2
1
最简公分母为
方程两边乘 ,得 .
解:
.
.
.
解得 .
检验:当 时,.
是原分式方程的解.
最简公分母为
方程两边乘 ,得
解:
.
.
.
解得 .
检验:当 时,.
原分式方程无解.
2
归纳
解分式方程的基本思路:
将分式方程化为整式方程.
具体做法:
去分母,方程左右两边同乘最简公分母.
归纳
解分式方程的步骤:
去分母(两边同乘最简公分母);
1
解整式方程;
2
检验(代入最简公分母);
3
写出原分式方程的解.
4
课
堂
小
结
分式方程的概念
分母中含有未知数的方程,叫做分式方程.
解分式方程的基本思路
将分式方程化为整式方程.
数学方法
将未知转化为已知,复杂转化为简单的化归思想.
课
堂
小
结
分式方程
去分母
解整式方程
检验
整式方程
不是分式方程的解
是分式方程的解
最简公分母不为
最简公分母为
目标
解分式方程的一般步骤
课后作业
解方程:
1
2
3
再 见
分式方程
(第一课时)
情景引入
分析
,
顺
静
水流
.
逆
静
水流
一艘轮船在静水中的最大航速为 千米/时,它沿江以最大航速顺流航行 千米所用时间与以最大航速逆流航行 千米所用时间相等,江水的水流速度为多少?
一艘轮船在静水中的最大航速为 千米/时,它沿江以最大航速顺流航行 千米所用时间与以最大航速逆流航行 千米所用时间相等,江水的水流速度为多少?
路程(千米)
速度(千米/时)
时间(小时)
顺水
逆水
分析:设水流速度为 千米/时.
路程(千米)
速度(千米/时)
时间(小时)
顺水
逆水
所用时间相等
等量关系:
顺流航行 千米的时间逆流航行 千米的时间
温故知新
方程:含有未知数的等式叫方程.
一元一次方程
二元一次方程
含有一个未知数,且未知数项的次数为一的整式方程.
含有两个未知数,且含有未知数的项的次数为一的整式方程.
整式方程
概念
分母中含有未知数的方程,叫做分式方程.
特征
1
等式;
2
分母中含有未知数.
巩固定义
下列关于 的方程中哪些是分式方程?为什么?
例
1
2
3
5
4
6
解方程
例
去分母,得 .
去括号,得 .
解:
移项,得
合并同类项,得
系数化为 ,得
探究分式方程的解法
整式方程
分式方程
去分母
最简公分母为
.
去分母,两边同乘
.
去括号
.
移项
.
合并同类项
.
系数化为
解得 .
是原分式方程的解吗?
将 代入原方程,发现左边右边.
是原分式方程的解.
整式方程
分式方程
去分母
最简公分母为
.
去分母,两边同乘
.
移项
.
合并同类项
解得 .
是原分式方程的解吗?
当 时,左边和右边分式的分母都为 ,分式无意义.
不是原分式方程的解.
.
同乘
.
去括号
.
移项
.
合并同类项
.
系数化为
去分母
.
同乘
.
移项
.
合并同类项
去分母
.
同乘
去分母
.
同乘
去分母
解得 .
解得 .
检验是解分式方程的必要步骤
如何更简便地检验呢?
将整式方程的解代入最简公分母,如果最简公分母的值不为 ,则整式方程的解是原分式方程的解;如果最简公分母的值为 ,这个解不是原分式方程的解.
解下列分式方程:
例
1
2
1
最简公分母为
方程两边乘 ,得 .
解:
.
.
.
解得 .
检验:当 时,.
是原分式方程的解.
最简公分母为
方程两边乘 ,得
解:
.
.
.
解得 .
检验:当 时,.
原分式方程无解.
2
归纳
解分式方程的基本思路:
将分式方程化为整式方程.
具体做法:
去分母,方程左右两边同乘最简公分母.
归纳
解分式方程的步骤:
去分母(两边同乘最简公分母);
1
解整式方程;
2
检验(代入最简公分母);
3
写出原分式方程的解.
4
课
堂
小
结
分式方程的概念
分母中含有未知数的方程,叫做分式方程.
解分式方程的基本思路
将分式方程化为整式方程.
数学方法
将未知转化为已知,复杂转化为简单的化归思想.
课
堂
小
结
分式方程
去分母
解整式方程
检验
整式方程
不是分式方程的解
是分式方程的解
最简公分母不为
最简公分母为
目标
解分式方程的一般步骤
课后作业
解方程:
1
2
3
再 见
