15.2.3 整数指数幂 课件(共23张PPT)
文档属性
| 名称 | 15.2.3 整数指数幂 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 21:17:59 | ||
图片预览






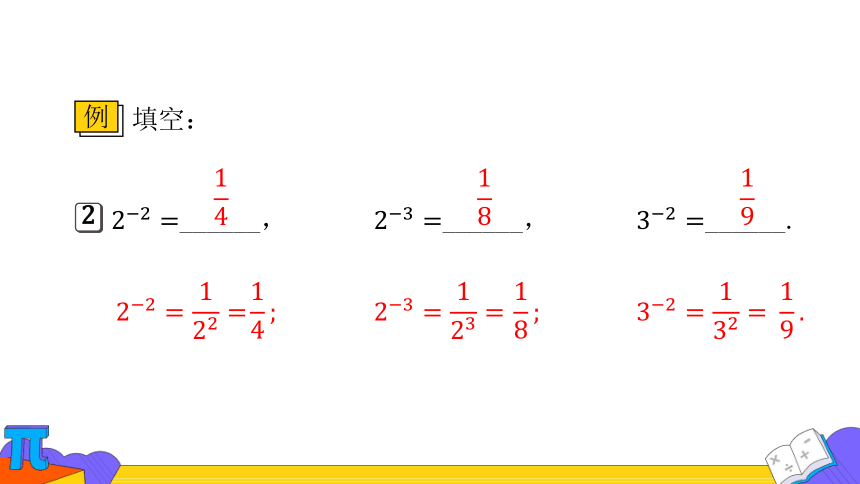
文档简介
(共23张PPT)
整数指数幂
复习回顾
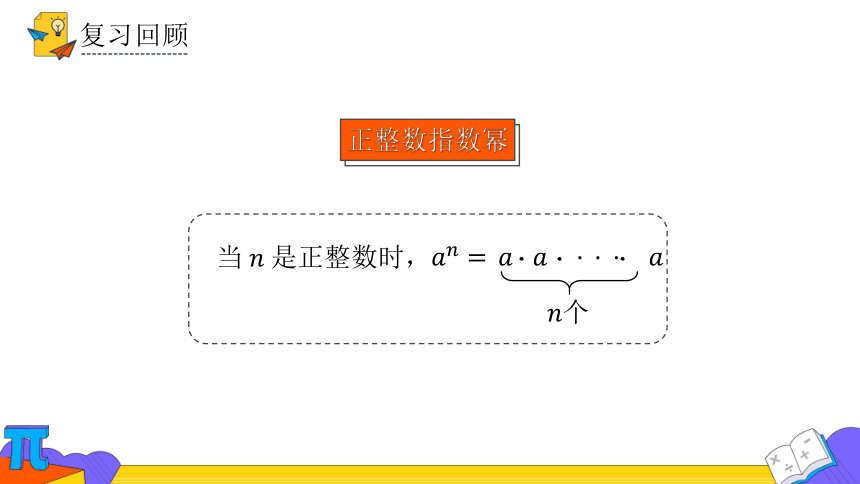
正整数指数幂
当是正整数时,
· ·
个
·
·
·
复习回顾
正整数指数幂的运算性质
;
1
;
2
;
3
;
4
5
.
复习回顾
指数幂
当时,.
指数可以是正整数,也可以是.
中的指数可以是负整数吗?
如果可以,那么负整数指数幂表示什么?
当时,
,
.
.
假设
在数学上,我们规定:
当是正整数时, .
在数学上,我们规定:
当是正整数时, .
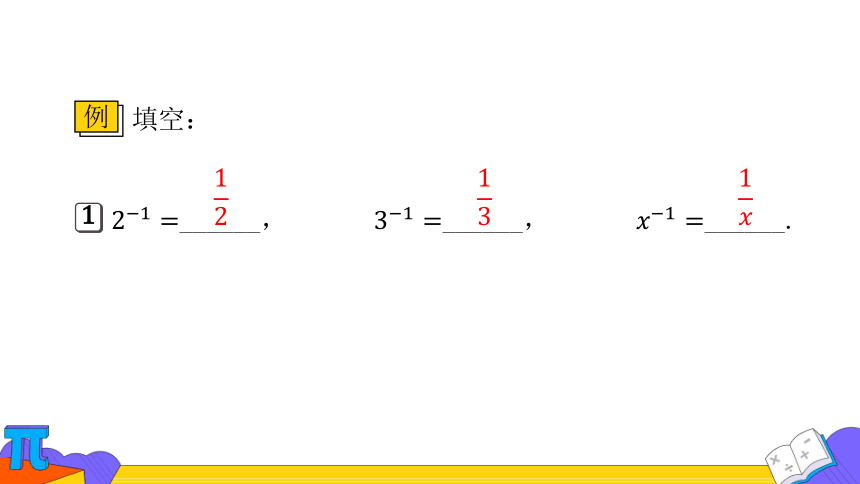
填空:
例
______,
1
______,
______.
填空:
例
______,
2
______,
______.
填空:
例
______,
3
______.
______,
填空:
例
3
指数的作用范围
注意
______.
以这条性质为例:
1
引入负数指数和指数后,正整数指数幂的其他几条运算性质能否推广到是任意整数的情形?
引入负数指数和指数后,正整数指数幂的其他几条运算性质能否推广到是任意整数的情形?
以这条性质为例:
1
;
2
以这条性质为例:
;
3
.
1
;
2
引入负数指数和指数后,正整数指数幂的其他几条运算性质能否推广到是任意整数的情形?
整数指数幂具有以下运算性质
;
1
;
2
;
3
;
4
5
;
6
填空:
例
;
1
解:
.
;
2
.
解:
;
3
.
解:
我们知道绝对值大于等于 1 的数都能用科学记数法表示,那么绝对值小于 1 的数,例如 0.0002 能否用科学记数法表示呢?
0.0002
= 20.0001
= 2
= 2
= 2.
绝对值小于的数可以用科学记数法表示为 的形式,其中,是正整数.
指数的确定
小数点从的后面向左移动了位.
.
方法
在确定了左起第一个不为的数字后,通过小数点向左移动了几位来确定指数.
指数的确定
用科学记数法表示下列数:
例
;
;
.
解:;
;
.
课
堂
小
结
负整数指数幂的意义:
1
整数指数幂的运算性质;
2
科学记数法的推广:
3
当是正整数时, .
绝对值小于的数可以用科学记数法表示为 的形式,其中,是正整数.
课后作业
填空:
,
1
计算:
2
;
1
;
2
3
.
.
,
用科学记数法表示下列数:
3
;
;
.
;
再 见
整数指数幂
复习回顾
正整数指数幂
当是正整数时,
· ·
个
·
·
·
复习回顾
正整数指数幂的运算性质
;
1
;
2
;
3
;
4
5
.
复习回顾
指数幂
当时,.
指数可以是正整数,也可以是.
中的指数可以是负整数吗?
如果可以,那么负整数指数幂表示什么?
当时,
,
.
.
假设
在数学上,我们规定:
当是正整数时, .
在数学上,我们规定:
当是正整数时, .
填空:
例
______,
1
______,
______.
填空:
例
______,
2
______,
______.
填空:
例
______,
3
______.
______,
填空:
例
3
指数的作用范围
注意
______.
以这条性质为例:
1
引入负数指数和指数后,正整数指数幂的其他几条运算性质能否推广到是任意整数的情形?
引入负数指数和指数后,正整数指数幂的其他几条运算性质能否推广到是任意整数的情形?
以这条性质为例:
1
;
2
以这条性质为例:
;
3
.
1
;
2
引入负数指数和指数后,正整数指数幂的其他几条运算性质能否推广到是任意整数的情形?
整数指数幂具有以下运算性质
;
1
;
2
;
3
;
4
5
;
6
填空:
例
;
1
解:
.
;
2
.
解:
;
3
.
解:
我们知道绝对值大于等于 1 的数都能用科学记数法表示,那么绝对值小于 1 的数,例如 0.0002 能否用科学记数法表示呢?
0.0002
= 20.0001
= 2
= 2
= 2.
绝对值小于的数可以用科学记数法表示为 的形式,其中,是正整数.
指数的确定
小数点从的后面向左移动了位.
.
方法
在确定了左起第一个不为的数字后,通过小数点向左移动了几位来确定指数.
指数的确定
用科学记数法表示下列数:
例
;
;
.
解:;
;
.
课
堂
小
结
负整数指数幂的意义:
1
整数指数幂的运算性质;
2
科学记数法的推广:
3
当是正整数时, .
绝对值小于的数可以用科学记数法表示为 的形式,其中,是正整数.
课后作业
填空:
,
1
计算:
2
;
1
;
2
3
.
.
,
用科学记数法表示下列数:
3
;
;
.
;
再 见
