15.3.2 分式方程 课件(共21张PPT)
文档属性
| 名称 | 15.3.2 分式方程 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
分式方程
(第二课时)
知识回顾
解分式方程时通过去分母将分式方程转化为整式方程,体会将未知转化为已知,复杂转化为简单的化归思想.
分式方程的概念
分母中含有未知数的方程,叫做分式方程.
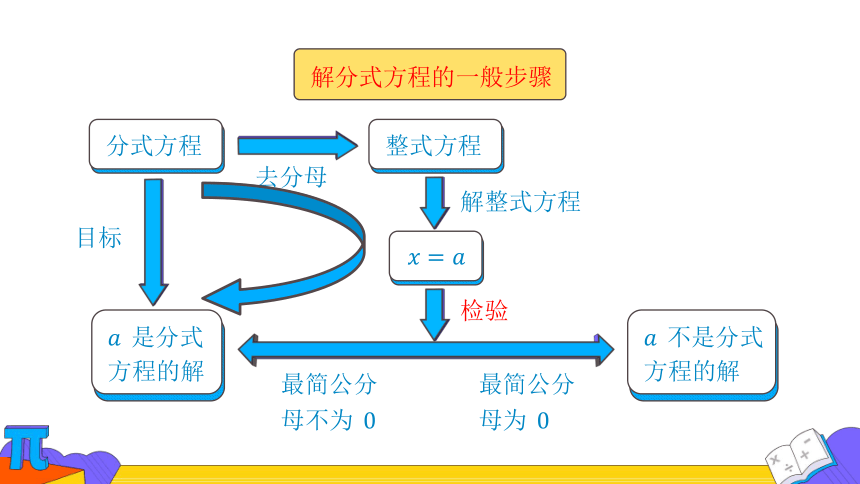
分式方程
去分母
解整式方程
检验
整式方程
不是分式方程的解
是分式方程的解
最简公分母不为
最简公分母为
目标
解分式方程的一般步骤
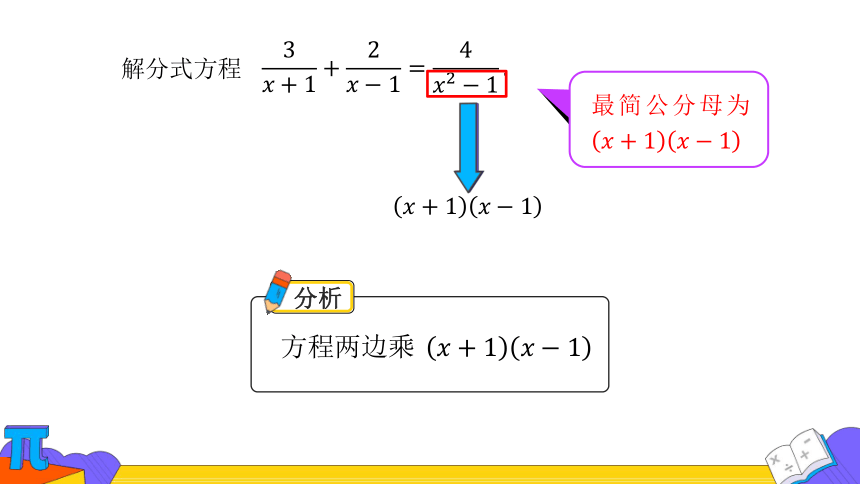
解分式方程
最简公分母为
方程两边乘
分析
解分式方程
方程两边乘 ,得
.
解:
.
.
最简公分母为
解得 .
检验:当 时,.
原分式方程无解.
解下列分式方程:
例
1
2
解下列分式方程:
例
1
分母是多项式
可以分解因式
原方程可化为
最简公分母为
分析
变形,得
解:
.
.
.
.
最简公分母为
方程两边乘 ,得
解得
检验:当 时,.
是原分式方程的解.
多项式加括号
乘任何数都为
解下列分式方程:
例
变形,得
最简公分母为
2
解:
整理,得
最简公分母为
整理,得
方程两边乘 ,得
.
.
.
.
解得 .
检验:当 时,.
是原分式方程的解.
小结
当分式方程中含有可分解因式的多项式时,先将其进行因式分解,可方便确定最简公分母;
1
分母因式分解后,观察分式的分子和分母,能约分的要先约分,可方便计算;
2
去分母后是多项式时,一定要加括号;
3
解分式方程一定要检验.
4
解下列分式方程:
练习
1
2
3
解下列分式方程:
练习
1
变形,得
最简公分母为
解:
最简公分母为
变形,得
方程两边乘 ,得
.
.
.
.
解得 .
检验:当 时,.
原分式方程无解.
不要漏乘不含分母的项
解下列分式方程:
练习
变形,得
最简公分母为
解:
2
最简公分母为
变形,得
方程两边乘 ,得
.
.
.
.
解得 .
检验:当 时,.
是原分式方程的解.
解下列分式方程:
练习
变形,得
最简公分母为
解:
3
互为相反数
变形,得
解:
.
.
.
.
最简公分母为
方程两边乘 ,得
解得
检验:当 时,.
是原分式方程的解.
课
堂
小
结
解较复杂分式方程时,先变形整理,能约分的先约分,可方便确定最简公分母;
1
注意每一步变形都要有依据,去分母时,不要漏乘不含分母的项;
2
互为相反数的多项式,可通过对其中一个提取负号实现统一;
3
解分式方程一定要检验.
4
课后作业
解方程:
1
2
3
再 见
分式方程
(第二课时)
知识回顾
解分式方程时通过去分母将分式方程转化为整式方程,体会将未知转化为已知,复杂转化为简单的化归思想.
分式方程的概念
分母中含有未知数的方程,叫做分式方程.
分式方程
去分母
解整式方程
检验
整式方程
不是分式方程的解
是分式方程的解
最简公分母不为
最简公分母为
目标
解分式方程的一般步骤
解分式方程
最简公分母为
方程两边乘
分析
解分式方程
方程两边乘 ,得
.
解:
.
.
最简公分母为
解得 .
检验:当 时,.
原分式方程无解.
解下列分式方程:
例
1
2
解下列分式方程:
例
1
分母是多项式
可以分解因式
原方程可化为
最简公分母为
分析
变形,得
解:
.
.
.
.
最简公分母为
方程两边乘 ,得
解得
检验:当 时,.
是原分式方程的解.
多项式加括号
乘任何数都为
解下列分式方程:
例
变形,得
最简公分母为
2
解:
整理,得
最简公分母为
整理,得
方程两边乘 ,得
.
.
.
.
解得 .
检验:当 时,.
是原分式方程的解.
小结
当分式方程中含有可分解因式的多项式时,先将其进行因式分解,可方便确定最简公分母;
1
分母因式分解后,观察分式的分子和分母,能约分的要先约分,可方便计算;
2
去分母后是多项式时,一定要加括号;
3
解分式方程一定要检验.
4
解下列分式方程:
练习
1
2
3
解下列分式方程:
练习
1
变形,得
最简公分母为
解:
最简公分母为
变形,得
方程两边乘 ,得
.
.
.
.
解得 .
检验:当 时,.
原分式方程无解.
不要漏乘不含分母的项
解下列分式方程:
练习
变形,得
最简公分母为
解:
2
最简公分母为
变形,得
方程两边乘 ,得
.
.
.
.
解得 .
检验:当 时,.
是原分式方程的解.
解下列分式方程:
练习
变形,得
最简公分母为
解:
3
互为相反数
变形,得
解:
.
.
.
.
最简公分母为
方程两边乘 ,得
解得
检验:当 时,.
是原分式方程的解.
课
堂
小
结
解较复杂分式方程时,先变形整理,能约分的先约分,可方便确定最简公分母;
1
注意每一步变形都要有依据,去分母时,不要漏乘不含分母的项;
2
互为相反数的多项式,可通过对其中一个提取负号实现统一;
3
解分式方程一定要检验.
4
课后作业
解方程:
1
2
3
再 见
