青岛版淄博市六年级上册数学期末经典题目练习卷1(含答案)
文档属性
| 名称 | 青岛版淄博市六年级上册数学期末经典题目练习卷1(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 15:51:20 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
淄博市六年级上册数学期末试卷训练经典题目(含答案)
一、填空题
1、填上合适的单位。
(1)一间教室的内部空间约是60( )。
(2)一只墨水瓶的容积约是60( )。
(3)一瓶酱油的质量约是500( )。
(4)一桶纯净水的体积约是20( )。
2、根据下图中的数据,手指和掌心长度的最简整数比是( ),比值是( )。
3、学校合唱队男生人数比女生少,女生人数比男生多_______,据统计合唱队人数有70多人,合唱队中男生有_______人。
4、一台拖拉机小时耕地公顷,这台拖拉机平均每小时耕地( )公顷,耕6公顷地需要( )小时。
5、如图,长方形长为10厘米,宽为6厘米,一个直径为2厘米的圆在长方形内部沿长方形四条边滚动一周,它所扫过的面积为______平方厘米。
6、一种药水是把药粉和水按1∶25配成。要配制这种药水624千克,需要水______千克;如果有80克水,配成这种药水需要加______克药粉。
7、◎+☆=48,◎=☆十☆十☆,◎=( ),☆=( )。
8、在( )里填上“<”“>”或“=”。
( ) ( )
( ) ( )
9、修一条2km长的公路,若每天修它的,要( )天修完;若每天修km,要( )天修完。
10、用小棒摆正六边形(如下图)。
(1)摆5个正六边形需要( )根小棒;用101根小棒能摆( )个正六边形。
(2)摆个正六边形需要( )根小棒。
二、选择题
11、下面说法正确的是( )。
A.以半圆为弧的扇形的圆心角是180°。
B.在同一个圆里,两条半径就组成一条直径。
C.一根绳子长1米,用去49厘米,还剩51%米。
D.要表示各部分数量与总数之间的关系,应选用折线统计图。
12、两根同样长的绳子,第一根用去米,第二根用去,两根绳子剩下的长度( )。
A.无法确定 B.第一根长 C.一样长
13、六二班男生人数比女生人数多20%,女生人数占全班的( )。
A. B. C.
14、甲加工3个零件用40分,乙加工4个零件用30分,甲、乙工作效率的比是( )。
A.3∶4 B.4∶3 C.9∶16
15、下面各组中的两个数互为倒数的是( )。
A.和7 B.和 C.1和 D.和0.5
16、在比例尺是1∶16的图纸上,甲、乙两个圆的半径比是3∶5,那么这两个圆的实际面积比是( )。
A.3∶5 B.1∶16 C.48∶80 D.9∶25
17、欢欢和乐乐是集邮爱好者,已知欢欢邮票张数的和乐乐邮票张数的相等,那么欢欢和乐乐邮票张数的比是( )。
A. B. C.28∶25 D.25∶28
18、下图中阴影部分占整个长方形面积的( )。
A. B. C. D.
三、解答题
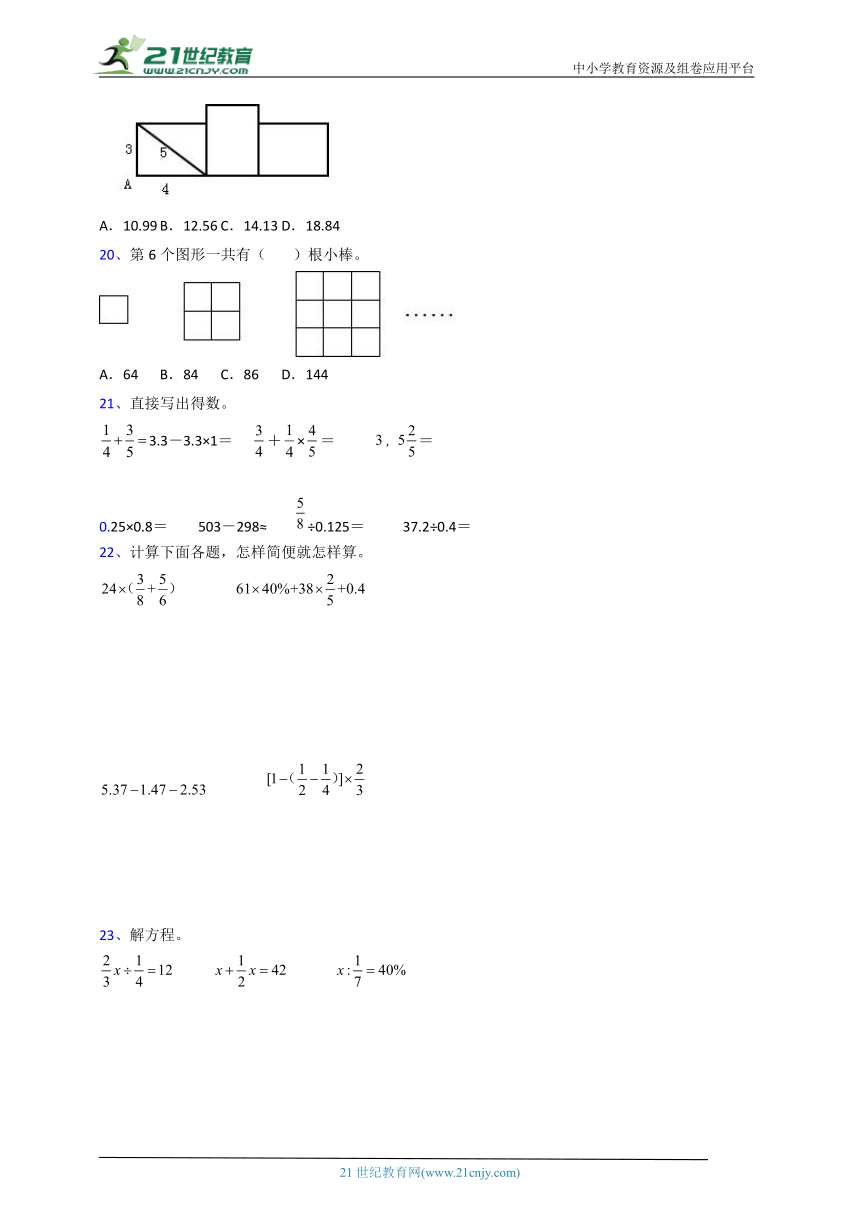
19、如图所示,一个长方形连续向右滚动2次,顶点滚动经过的路线全长( )厘米。(值取3.14)
A.10.99 B.12.56 C.14.13 D.18.84
20、第6个图形一共有( )根小棒。
A.64 B.84 C.86 D.144
21、直接写出得数。
3.3-3.3×1= +×= =
0.25×0.8= 503-298≈ ÷0.125= 37.2÷0.4=
22、计算下面各题,怎样简便就怎样算。
23、解方程。
24、计算图中阴影部分的面积。
25、一本童话书有160页,胡兵第一周读了这本书的,第二周读了余下的,第二周读了多少页?
26、超音速飞机的飞行速度可达到1500千米/时,磁悬浮列车的运行速度比它慢。磁悬浮列车的速度是多少?
27、如图,长方形的长AD与宽AB的比为5∶3,E、F为 AB边上的三等分点,某时刻,甲从A点出发沿长方形逆时针运动,与此同时,乙、丙分别从E、F出发沿长方形顺时针运动。甲、乙、丙三人的速度比为4∶3∶5,他们出发后12分钟,三人所在位置的点的连线第一次构成长方形中最大的三角形,那么再过多少分钟,三人所在位置的点的连线第二次构成最大三角形?
28、一个书架上下两层共有图书450本,如果将上层书增加它的,下层书增加它的,这时上、下两层图书的本数就一样多.这个书架原来上、下层各有图书多少本?
29、五年级学生举行“最爱吃的水果”投票活动(每人均有投票,且只能投1种水果),结果如图。
(1)如果从五年级学生中随意抽取一人,这人最爱吃的水果是( )的可能性最大;
(2)如果五年级学生中最爱吃香蕉和葡萄的同学共有78人,那么五年级一共有学生多少人?
30、一瓶洗衣液,第一周用了总量的,第二周用了总量的20%,还剩2.2升,这瓶洗衣液原有多少升?
31、有苹果、梨、桃、枣四种水果,已知苹果和梨占总重量的,梨和桃占总重量的45%,枣占总重量的30%,又知桃比苹果多42千克。枣有多少千克?
【参考答案】
一、填空题
1、 立方米 毫升 克
升
【解析】
根据生活经验、对体积单位、容积单位和质量单位的认识以及数据的大小,选择适当的计量单位即可。
(1)一间教室的内部空间约是60立方米。
(2)一只墨水瓶的容积约是60毫升。
(3)一瓶酱油的质量约是500克。
(4)一桶纯净水的体积约是20升。
【点睛】
此题考查了根据情境选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活选择。
2、 3∶4 0.75
【解析】
用手指长度比掌心长度,利用“比的基本性质”把比化简成最简整数比,即前项和后项都是整数,且互质。求比值是把比号转化成除号,进行除法运算,结果是一个数值。
7.5∶10
=(7.5×10)∶(10×10)
=75∶100
=(75÷25)∶(100÷25)
=3∶4
7.5∶10
=7.5÷10
=0.75
【点睛】
区分化简比和求比值的不同是解题的关键。
3、 32
【解析】
把女生人数看作单位“1”,则男生人数就是(1-),求女生人数比男生多几分之几,女生比男生多的部分除以男生人数;把女生人数看作5份,则男生人数就是4份,即女生与男生人数的比是5∶4,人数不能为分数或小数,合唱队人数在71到79之间,且是(5+4)的倍数,据此即可求出合唱队人数。把合唱人数除以(5+4)求出1份人数,再乘4,就是男生人数。
÷(1-)
=÷
=
把女生人数看作5份,则男生人数就是4份,即女生人数与男生人数的比是5∶4
5+4=9
……
9×7=63(人),不合题意
9×8=72(人),符合题意
9×9=81(人),不合题意
即合唱队有72人
72÷(5+4)×4
=72÷9×4
=32(人)
【点睛】
第一空:求一个数比另一个数多或少几分之几,用这两数之差除以另一个数;第二空:求出女生与男生人数的比是最简整数比,再根据按比例分配问题解答。
4、
【解析】
平均每小时耕地多少公顷,要用耕地的总面积除以时间,相当于是工作效率,然后用工作总量6公顷除以工作效率,得到工作时间。
÷=(公顷/小时)
6÷=(小时)
【点睛】
本题考查的是工程问题,工作效率=工作总量÷工作时间,工作时间=工作总量÷工作效率工作效率=工作总量÷工作时间,工作时间=工作总量÷工作效率。
5、14
【解析】
,如图所示,它所扫过的面积=大长方形的面积-中间空白长方形的面积-四个角的空白部分,其中四个角的空白部分=边长为2厘米的正方形的面积-直径为2厘米圆的面积,据此解答。
2÷1=1(厘米)
10×6-(10-2×2)×(6-2×2)-(2×2-3.14×12)
=60-6×2-0.86
=47.14(平方厘米)
它所扫过的面积为47.14平方厘米。
【点睛】
此题考查了有关圆的面积计算,明确所求面积包含哪些部分是解题关键。
6、 600 3.2
【解析】
根据药粉和水的比以及药水的总质量,按比例分配,先求出1份的质量,再乘水所占份数即可;已知水的质量,根据药粉和水的比,可先求出1份的质量,也就是需要药粉的质量。
624÷(25+1)×25
=24×25
=600(千克),需要水600千克;
80÷25×1=3.2(克),配成这种药水需要加3.2克药粉。
【点睛】
此题主要考查了比的应用,找出量对应的份数,先求出1份的量是解题关键。
7、 36 12
【解析】
由于◎+☆=48,◎=☆十☆十☆,则☆=48÷4=12, ◎是3个☆相加,则一个◎:12×3=36
☆=48÷(1+3)=48÷4=12
◎=12×3=36
【点睛】
正确理解等量代还的意义,是解答此题的关键。
8、 < > < >
【解析】
和根据积和乘数的关系,如果其中一个乘数大于1,则积大于另一个乘数,如果其中一个乘数小于1,则积小于另一个乘数,由此即可比较;
和根据商和被除数的关系,如果除数大于1,则商小于被除数,如果除数小于1,则商大于被除数,由于>12,<12;由此即可比较;
和根据商和被除数的关系即可比较;
和由于的除数小于1,则>6;中的<1,则<6,由此即可比较。
<
>
<
>
【点睛】
本题主要考查被除数和商的关系以及积和乘数的关系,熟练掌握它们之间的关系并灵活运用。
9、 10 20
【解析】
(1)把工作总量看作单位“1”, 需要的天数=1÷每天修的长度占全长的分率;
(2)这条公路总长度是2千米,每天修km,根据“工作时间=工作总量÷工作效率”即可求得。
(1)1÷=10(天)
(2)2÷=20(天)
【点睛】
掌握工作总量、工作时间、工作效率之间的关系是解答题目的关键。
10、(1) 26 20
(2)
【解析】
(1)观察可知:摆一个正六边形要5×1+1=6根小棒;摆2个正六边形要5×2+1=11根;摆3个正六边形要5×3+1=16根;摆5个正六边形要5×5+1=26根;101根小棒可以摆(101-1)÷5=20个。
(2)摆n个正六边形要5n+1根小棒。
(1)
摆5个正六边形需要(26)根小棒;用101根小棒能摆(20)个正六边形。
(2)
摆个正六边形需要(5n+1)根小棒。
【点睛】
本题考查了观察能力了推理归纳能力。从图形的摆放中发现规律,利用规律是解答本题的关键。
二、选择题
12.A
解析:A
【解析】
逐项分析:
A.经过圆心的两条半径所组成的角叫做圆心角,据此判断;
B.通过圆心且两端都在圆上的线段叫做直径,据此判断;
C.根据百分数的意义:表示一个数是另一个数的百分之几,是一个比,不带单位;
D.扇形统计图的特点:表示各部分数量与总数之间的关系,据此判断。
由分析得,
A.以半圆为弧的扇形的圆心角是180°正确;
B.在同一个圆里,通过圆心且两端都在圆上的线段叫做直径,故此题错误;
C.100-49=51(厘米),51÷100=51%,应剩下1米的51%,故此题错误;
D.要表示各部分数量与总数之间的关系,应选扇形统计图,故此题错误。
故选:A
【点睛】
此题考查的是基础知识的应用,熟练掌握基础知识是解题关键。
13.A
解析:A
【解析】
假设两根绳子的长度等于1米,大于1米,小于1米(大于米)时的长度,分别计算剩下部分的长度并比较大小即可。
情况1:假设两根绳子的长度为1米。
第一根绳子剩下的长度:1-=(米)
第二根绳子剩下的长度:1×(1-)=(米)
则两根绳子剩下的长度相等。
情况2:假设两根绳子的长度为2米。
第一根绳子剩下的长度:2-=(米)
第二根绳子剩下的长度:2×(1-)=(米)
米>米,则第一根绳子剩下的长度长。
情况3:假设两根绳子的长度为米。
第一根绳子剩下的长度:-=(米)
第二根绳子剩下的长度:×(1-)=(米)
米<米,则第二根绳子剩下的长度长。
所以两根绳子剩下的长度无法比较。
故答案为:A
【点睛】
题目中第一个是具体的量,第二个是分率,绳子的长度不确定时剩下的长度无法比较。
14.B
解析:B
【解析】
根据男生人数比女生人数多20%,女生人数是单位“1”,则男生人数占女生人数的1+20%,全班人数占女生人数的1+1+20%,求女生人数占全班的几分之几,用1÷全班对应百分率即可。
1÷(1+1+20%)
=1÷2.2
=
故答案为:B
【点睛】
关键是理解百分数的意义,此类问题一般用表示单位“1”的量作除数。
15.C
解析:C
【解析】
本题可先通过他们各自加工零件的个数及用时求出他们的工作效率,然后就能求出两者的效率比。
甲的工作效率为:3÷40=
乙的工作效率为:4÷30=
甲乙工作效率的比为∶=9∶16
故答案为:C
【点睛】
结果是比的问题一般要将结果根据比的基本性质化为最简整数比。
16.A
解析:A
【解析】
由倒数的定义可知,两个数乘积是1的数互为倒数。据此判断即可。
A.和7,,符合题意;
B.和,,不符合题意;
C.1和,,,不符合题意;
D.和0.5,,不符合题意;
故答案为:A
【点睛】
此题的解题关键是掌握倒数的概念和特点,得出正确的选项。
17.D
解析:D
【解析】
根据圆的面积公式:S=πr2,可得圆的面积比等于半径的平方比;也可以根据半径比3∶5,假设甲、乙两个圆的半径,根据比例尺求出两个圆的实际半径比,再用圆的面积公式求出面积比,据此解答。
3×3=9
5×5=25
所以这两个圆的实际面积比是9∶25。
故答案为:D
【点睛】
解答此题的关键是理解图上距离、实际距离、和比例尺的关系,以及圆的面积公式。
18.D
解析:D
【解析】
因为欢欢邮票张数的和乐乐邮票张数的相等,所以欢欢邮票张数×=乐乐邮票张数×,再逆用比例的基本性质作答,即在比例里,两个外项的积等于两个内项的积求出欢欢和乐乐邮票张数的比。
因为欢欢邮票张数×=乐乐邮票张数×
所以欢欢邮票张数∶乐乐邮票张数=∶=25∶28
故答案为:D
【点睛】
本题主要是根据题意得出数量关系式,再灵活利用比例的基本性质解决问题。
19.D
解析:D
【解析】
假设小正方形边长为1,求出整个长方形和阴影部分三角形的面积,阴影部分占整个长方形面积的分率=阴影部分的面积÷整个长方形的面积,结果化为最简分数,据此解答。
阴影部分的面积:4×1÷2=2
长方形的面积:5×1=5
2÷5=
故答案为:D
【点睛】
A占B的几分之几的计算方法:A÷B=,结果化为最简分数。
三、解答题
20.C
解析:C
【解析】
如图:
由A的位置到A1的位置时,所经过的路程是半径为4厘米的圆周长的,点A1的位置沿虚线到A2的位置时所经过的路程也是半径为5厘米的圆周长的,两次的路程之和就是顶点滚动经过的路线全长。
×3.14×2×4+×3.14×2×5
=6.28+7.85
=14.13(厘米)
故答案为:C
【点睛】
此题是考查图形的旋转、圆周长的计算等。图形旋转要注意四要素:即原位置、旋转中心、旋转方向、旋转角;圆的周长要弄清圆的半径。
21.B
解析:B
【解析】
由图可知,第1个图形每行1根小棒,一共2行,竖着每列有1根小棒,一共2列,一共有(2×2)根小棒;第2个图形横着每行有2根小棒,一共3行,竖着每列有2根小棒,一共有3列,一共有(2×3+3×2);第3个图形横着每行有3根小棒,一共4行,竖着每列有3根小棒,一共有4列,一共有(3×4+4×3)……第n个图形一共有n(n+1)+ n(n+1),化简计算当n=6时式子的值,据此解答。
分析可知,第n个图形小棒的总根数为:n(n+1)+ n(n+1)=2n(n+1)根
当n=6时,2n(n+1)=2×6×(6+1)=2×6×7=12×7=84(根)
所以,第6个图形一共有84根小棒。
故答案为:B
【点睛】
找出图形个数与小棒根数变化的规律是解答题目的关键。
21、;0;;;
0.2;200;5;93
【解析】
22、29;40
1.37;
【解析】
(1)运用乘法分配律进行简算;
(2)运用乘法分配律进行简算;
(3)运用减法性质进行简算;
(4)先算小括号里的减法,再算中括号里的减法,最后算括号外的乘法。
24×(+)
=24×+24×
=9+20
=29;
61×40%+38×+0.4
=(61+38+1)×40%
=100×40%
=40;
5.37-1.47-2.53
=5.37-(1.47+2.53)
=5.37-4
=1.37;
[1-(-)]×
=[1-]×
=×
=
23、;x=28;
【解析】
解:
解:
x=28
解:
24、75cm2;7.125平方厘米
【解析】
第一幅图,两个扇形可以拼成一个半圆,阴影部分的面积=长方形面积-半圆面积;
第二幅图,阴影部分的面积=圆的面积-正方形面积,其中正方形面积可以用对角线的平方÷2进行计算。
5×2×5-3.14×5 ÷2
=50-39.25
=10.75(平方厘米)
3.14×(5÷2) -5×5÷2
=3.14×6.25-12.5
=19.625-12.5
=7.125(平方厘米)
26.48页
【解析】
根据题意先把这本书的总页数看是单位“1”,则第一天读了全书的,就还剩下全书的(1-)用乘法可求出剩下的页数,再把剩下的页数看是单位“1”,第二天读了余下的,用乘法可求出第二天读的页
解析:48页
【解析】
根据题意先把这本书的总页数看是单位“1”,则第一天读了全书的,就还剩下全书的(1-)用乘法可求出剩下的页数,再把剩下的页数看是单位“1”,第二天读了余下的,用乘法可求出第二天读的页数,据此解答。
160×(1-)×
=160××
=48(页)
答:第二周读了48页。
【点睛】
此题考查的是分数乘法的应用,解答此题关键是依据分数乘法的意义,注意两次单位“1”的不同。
27.500千米/时
【解析】
磁悬浮列车的运行速度比超音速飞机的飞行速度少,把超音速飞机的飞行速度看作单位“1”, 磁悬浮列车的速度是它的(1-),用超音速飞机的飞行速度乘这个分率,可求出磁悬浮列车的运
解析:500千米/时
【解析】
磁悬浮列车的运行速度比超音速飞机的飞行速度少,把超音速飞机的飞行速度看作单位“1”, 磁悬浮列车的速度是它的(1-),用超音速飞机的飞行速度乘这个分率,可求出磁悬浮列车的运行速度。
磁悬浮列车的速度:
1500×(1-)
=1500×
=500(千米/时)
答:磁悬浮列车的速度是500千米/时。
【点睛】
找准单位“1”的量是解此题的关键。
28.28分
【解析】
长方形内最大的三角形等于长方形面积的一半,这样的三角形一定有一条边与长方形的某条边重合,且另一个顶点恰好在该长方形的对边上。所以只要讨论三人中有两个人在长方形的顶点上的情况,因为长
解析:28分
【解析】
长方形内最大的三角形等于长方形面积的一半,这样的三角形一定有一条边与长方形的某条边重合,且另一个顶点恰好在该长方形的对边上。所以只要讨论三人中有两个人在长方形的顶点上的情况,因为长方形的长AD与宽AB的比为5∶3,所以将长方形的长5等份,宽3等份,将其周长分为16段,又因为甲、乙、丙三人的速度比为4∶3∶5,所以他们所行的路程比也是4∶3∶5,设甲走4段用1个单位时间,那么一个单位时间内乙、丙分别走3段、5段,由于4、3、5两两互质,所以在非整数单位时间内甲、乙、丙三人最多有一人走了整数段,所以只考虑整数单位时间。然后对到达顶点的情况一一列举即可,得到满足条件的单位时间点,再根据第一次构成长方形中最大的三角形的时间是12分钟,从而求出一个单位时间相当于多少分钟,根据列表知道第二次构成最大三角形需要几个时间单位,求出再过多少分钟,三人所在位置的点的连线第二次构成最大三角形,据此解答。
根据分析将长方形的长为5等份,宽为3等份,那么长方形的周长为16段,设甲走4段用1个单位时间,那么一个单位时间内乙、丙分别走3段、5段,根据分析又知道只有整数单位时间才符合题意,所以只考虑整数单位时间,所以三人到达顶点的情况列表如下:
甲 单位时间 2 4 6 8 10 12 14 16 ……
地点 C A C A C A C C ……
乙 单位时间 2 3 10 11 18 19 26 27 ……
地点 D C B A D C B A ……
丙 单位时间 2 3 10 11 18 19 26 27 ……
地点 C B A D C B A D ……
通过列表可知2个单位时间时,甲和丙重合,不满足条件,3个单位时间时,甲在AD上,三人第一次构成最大的三角形,所以一个单位时间为12÷3=4(分);
10个单位时间的时候甲、乙、丙分别在C、B、A点上,第二次构成最大的三角形,
4×10-12
=40-12
=28(分)
答:再过28分钟,三人所在位置的点的连线第二次构成最大三角形。
【点睛】
此题考查的是行程问题,解题的关键是理解长方形内最大的三角形等于长方形面积的一半。
29.上层200本,下层250本
【解析】
解:设上层书架原有x本书,则下层书架原有(450﹣x)本,得
(1+)x=(450﹣x)×(1+)
x=(450﹣x)×
x=585﹣x
x=585
x=200
解析:上层200本,下层250本
【解析】
解:设上层书架原有x本书,则下层书架原有(450﹣x)本,得
(1+)x=(450﹣x)×(1+)
x=(450﹣x)×
x=585﹣x
x=585
x=200
450﹣200=250(本)
答:原来上层书架有图书200本、下层书架有图书250本.
30.(1)苹果;
(2)200人
【解析】
(1)扇形统计图中哪种水果所占的面积最大,最爱吃该种水果的可能性最大;
(2)把五年级学生总人数看作单位“1”,最爱吃香蕉和葡萄的同学占总人数的(23%+16
解析:(1)苹果;
(2)200人
【解析】
(1)扇形统计图中哪种水果所占的面积最大,最爱吃该种水果的可能性最大;
(2)把五年级学生总人数看作单位“1”,最爱吃香蕉和葡萄的同学占总人数的(23%+16%),根据“量÷对应的分率”求出五年级的总人数。
(1)分析可知,如果从五年级学生中随意抽取一人,这人最爱吃的水果是苹果的可能性最大。
(2)78÷(23%+16%)
=78÷0.39
=200(人)
答:五年级一共有学生200人。
【点睛】
已知一个数的百分之几是多少,求这个数用除法计算。
31.4升
【解析】
把这瓶洗衣液原有的升数看作单位“1”, 第一周用了总量的,第二周用了总量的20%,还剩下(1--20%),还剩下的2.2升,用“剩下的体积÷对应的分率”用除法计算即可。
2.2÷(1
解析:4升
【解析】
把这瓶洗衣液原有的升数看作单位“1”, 第一周用了总量的,第二周用了总量的20%,还剩下(1--20%),还剩下的2.2升,用“剩下的体积÷对应的分率”用除法计算即可。
2.2÷(1--20%)
=2.2÷(1-0.25-0.2)
=2.2÷0.55
=4(升)
答:这瓶洗衣液原有4升。
【点睛】
本题考查了分数、百分数复合应用题,关键是确定单位“1”,找到部分对应分率。
32.108千克
【解析】
把总质量看作单位“1”,用+45%+30%-1=求得梨所占总重量,进而求得苹果所占分率是-=,桃所占分率是45%-=,再用桃比苹果多42千克除以对应分率-求出总重量,再乘30%
解析:108千克
【解析】
把总质量看作单位“1”,用+45%+30%-1=求得梨所占总重量,进而求得苹果所占分率是-=,桃所占分率是45%-=,再用桃比苹果多42千克除以对应分率-求出总重量,再乘30%即可得到答案。
梨:+45%+30%-1
=-1
=
苹果:-=
桃:45%-=
42÷(-)
=42÷
=360(千克)
360×30%=108(千克)
答:枣有108千克。
【点睛】
此题考查的是分数、百分数应用,解答此题关键是找准单位“1”,明确数量间关系,列式解决问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
淄博市六年级上册数学期末试卷训练经典题目(含答案)
一、填空题
1、填上合适的单位。
(1)一间教室的内部空间约是60( )。
(2)一只墨水瓶的容积约是60( )。
(3)一瓶酱油的质量约是500( )。
(4)一桶纯净水的体积约是20( )。
2、根据下图中的数据,手指和掌心长度的最简整数比是( ),比值是( )。
3、学校合唱队男生人数比女生少,女生人数比男生多_______,据统计合唱队人数有70多人,合唱队中男生有_______人。
4、一台拖拉机小时耕地公顷,这台拖拉机平均每小时耕地( )公顷,耕6公顷地需要( )小时。
5、如图,长方形长为10厘米,宽为6厘米,一个直径为2厘米的圆在长方形内部沿长方形四条边滚动一周,它所扫过的面积为______平方厘米。
6、一种药水是把药粉和水按1∶25配成。要配制这种药水624千克,需要水______千克;如果有80克水,配成这种药水需要加______克药粉。
7、◎+☆=48,◎=☆十☆十☆,◎=( ),☆=( )。
8、在( )里填上“<”“>”或“=”。
( ) ( )
( ) ( )
9、修一条2km长的公路,若每天修它的,要( )天修完;若每天修km,要( )天修完。
10、用小棒摆正六边形(如下图)。
(1)摆5个正六边形需要( )根小棒;用101根小棒能摆( )个正六边形。
(2)摆个正六边形需要( )根小棒。
二、选择题
11、下面说法正确的是( )。
A.以半圆为弧的扇形的圆心角是180°。
B.在同一个圆里,两条半径就组成一条直径。
C.一根绳子长1米,用去49厘米,还剩51%米。
D.要表示各部分数量与总数之间的关系,应选用折线统计图。
12、两根同样长的绳子,第一根用去米,第二根用去,两根绳子剩下的长度( )。
A.无法确定 B.第一根长 C.一样长
13、六二班男生人数比女生人数多20%,女生人数占全班的( )。
A. B. C.
14、甲加工3个零件用40分,乙加工4个零件用30分,甲、乙工作效率的比是( )。
A.3∶4 B.4∶3 C.9∶16
15、下面各组中的两个数互为倒数的是( )。
A.和7 B.和 C.1和 D.和0.5
16、在比例尺是1∶16的图纸上,甲、乙两个圆的半径比是3∶5,那么这两个圆的实际面积比是( )。
A.3∶5 B.1∶16 C.48∶80 D.9∶25
17、欢欢和乐乐是集邮爱好者,已知欢欢邮票张数的和乐乐邮票张数的相等,那么欢欢和乐乐邮票张数的比是( )。
A. B. C.28∶25 D.25∶28
18、下图中阴影部分占整个长方形面积的( )。
A. B. C. D.
三、解答题
19、如图所示,一个长方形连续向右滚动2次,顶点滚动经过的路线全长( )厘米。(值取3.14)
A.10.99 B.12.56 C.14.13 D.18.84
20、第6个图形一共有( )根小棒。
A.64 B.84 C.86 D.144
21、直接写出得数。
3.3-3.3×1= +×= =
0.25×0.8= 503-298≈ ÷0.125= 37.2÷0.4=
22、计算下面各题,怎样简便就怎样算。
23、解方程。
24、计算图中阴影部分的面积。
25、一本童话书有160页,胡兵第一周读了这本书的,第二周读了余下的,第二周读了多少页?
26、超音速飞机的飞行速度可达到1500千米/时,磁悬浮列车的运行速度比它慢。磁悬浮列车的速度是多少?
27、如图,长方形的长AD与宽AB的比为5∶3,E、F为 AB边上的三等分点,某时刻,甲从A点出发沿长方形逆时针运动,与此同时,乙、丙分别从E、F出发沿长方形顺时针运动。甲、乙、丙三人的速度比为4∶3∶5,他们出发后12分钟,三人所在位置的点的连线第一次构成长方形中最大的三角形,那么再过多少分钟,三人所在位置的点的连线第二次构成最大三角形?
28、一个书架上下两层共有图书450本,如果将上层书增加它的,下层书增加它的,这时上、下两层图书的本数就一样多.这个书架原来上、下层各有图书多少本?
29、五年级学生举行“最爱吃的水果”投票活动(每人均有投票,且只能投1种水果),结果如图。
(1)如果从五年级学生中随意抽取一人,这人最爱吃的水果是( )的可能性最大;
(2)如果五年级学生中最爱吃香蕉和葡萄的同学共有78人,那么五年级一共有学生多少人?
30、一瓶洗衣液,第一周用了总量的,第二周用了总量的20%,还剩2.2升,这瓶洗衣液原有多少升?
31、有苹果、梨、桃、枣四种水果,已知苹果和梨占总重量的,梨和桃占总重量的45%,枣占总重量的30%,又知桃比苹果多42千克。枣有多少千克?
【参考答案】
一、填空题
1、 立方米 毫升 克
升
【解析】
根据生活经验、对体积单位、容积单位和质量单位的认识以及数据的大小,选择适当的计量单位即可。
(1)一间教室的内部空间约是60立方米。
(2)一只墨水瓶的容积约是60毫升。
(3)一瓶酱油的质量约是500克。
(4)一桶纯净水的体积约是20升。
【点睛】
此题考查了根据情境选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活选择。
2、 3∶4 0.75
【解析】
用手指长度比掌心长度,利用“比的基本性质”把比化简成最简整数比,即前项和后项都是整数,且互质。求比值是把比号转化成除号,进行除法运算,结果是一个数值。
7.5∶10
=(7.5×10)∶(10×10)
=75∶100
=(75÷25)∶(100÷25)
=3∶4
7.5∶10
=7.5÷10
=0.75
【点睛】
区分化简比和求比值的不同是解题的关键。
3、 32
【解析】
把女生人数看作单位“1”,则男生人数就是(1-),求女生人数比男生多几分之几,女生比男生多的部分除以男生人数;把女生人数看作5份,则男生人数就是4份,即女生与男生人数的比是5∶4,人数不能为分数或小数,合唱队人数在71到79之间,且是(5+4)的倍数,据此即可求出合唱队人数。把合唱人数除以(5+4)求出1份人数,再乘4,就是男生人数。
÷(1-)
=÷
=
把女生人数看作5份,则男生人数就是4份,即女生人数与男生人数的比是5∶4
5+4=9
……
9×7=63(人),不合题意
9×8=72(人),符合题意
9×9=81(人),不合题意
即合唱队有72人
72÷(5+4)×4
=72÷9×4
=32(人)
【点睛】
第一空:求一个数比另一个数多或少几分之几,用这两数之差除以另一个数;第二空:求出女生与男生人数的比是最简整数比,再根据按比例分配问题解答。
4、
【解析】
平均每小时耕地多少公顷,要用耕地的总面积除以时间,相当于是工作效率,然后用工作总量6公顷除以工作效率,得到工作时间。
÷=(公顷/小时)
6÷=(小时)
【点睛】
本题考查的是工程问题,工作效率=工作总量÷工作时间,工作时间=工作总量÷工作效率工作效率=工作总量÷工作时间,工作时间=工作总量÷工作效率。
5、14
【解析】
,如图所示,它所扫过的面积=大长方形的面积-中间空白长方形的面积-四个角的空白部分,其中四个角的空白部分=边长为2厘米的正方形的面积-直径为2厘米圆的面积,据此解答。
2÷1=1(厘米)
10×6-(10-2×2)×(6-2×2)-(2×2-3.14×12)
=60-6×2-0.86
=47.14(平方厘米)
它所扫过的面积为47.14平方厘米。
【点睛】
此题考查了有关圆的面积计算,明确所求面积包含哪些部分是解题关键。
6、 600 3.2
【解析】
根据药粉和水的比以及药水的总质量,按比例分配,先求出1份的质量,再乘水所占份数即可;已知水的质量,根据药粉和水的比,可先求出1份的质量,也就是需要药粉的质量。
624÷(25+1)×25
=24×25
=600(千克),需要水600千克;
80÷25×1=3.2(克),配成这种药水需要加3.2克药粉。
【点睛】
此题主要考查了比的应用,找出量对应的份数,先求出1份的量是解题关键。
7、 36 12
【解析】
由于◎+☆=48,◎=☆十☆十☆,则☆=48÷4=12, ◎是3个☆相加,则一个◎:12×3=36
☆=48÷(1+3)=48÷4=12
◎=12×3=36
【点睛】
正确理解等量代还的意义,是解答此题的关键。
8、 < > < >
【解析】
和根据积和乘数的关系,如果其中一个乘数大于1,则积大于另一个乘数,如果其中一个乘数小于1,则积小于另一个乘数,由此即可比较;
和根据商和被除数的关系,如果除数大于1,则商小于被除数,如果除数小于1,则商大于被除数,由于>12,<12;由此即可比较;
和根据商和被除数的关系即可比较;
和由于的除数小于1,则>6;中的<1,则<6,由此即可比较。
<
>
<
>
【点睛】
本题主要考查被除数和商的关系以及积和乘数的关系,熟练掌握它们之间的关系并灵活运用。
9、 10 20
【解析】
(1)把工作总量看作单位“1”, 需要的天数=1÷每天修的长度占全长的分率;
(2)这条公路总长度是2千米,每天修km,根据“工作时间=工作总量÷工作效率”即可求得。
(1)1÷=10(天)
(2)2÷=20(天)
【点睛】
掌握工作总量、工作时间、工作效率之间的关系是解答题目的关键。
10、(1) 26 20
(2)
【解析】
(1)观察可知:摆一个正六边形要5×1+1=6根小棒;摆2个正六边形要5×2+1=11根;摆3个正六边形要5×3+1=16根;摆5个正六边形要5×5+1=26根;101根小棒可以摆(101-1)÷5=20个。
(2)摆n个正六边形要5n+1根小棒。
(1)
摆5个正六边形需要(26)根小棒;用101根小棒能摆(20)个正六边形。
(2)
摆个正六边形需要(5n+1)根小棒。
【点睛】
本题考查了观察能力了推理归纳能力。从图形的摆放中发现规律,利用规律是解答本题的关键。
二、选择题
12.A
解析:A
【解析】
逐项分析:
A.经过圆心的两条半径所组成的角叫做圆心角,据此判断;
B.通过圆心且两端都在圆上的线段叫做直径,据此判断;
C.根据百分数的意义:表示一个数是另一个数的百分之几,是一个比,不带单位;
D.扇形统计图的特点:表示各部分数量与总数之间的关系,据此判断。
由分析得,
A.以半圆为弧的扇形的圆心角是180°正确;
B.在同一个圆里,通过圆心且两端都在圆上的线段叫做直径,故此题错误;
C.100-49=51(厘米),51÷100=51%,应剩下1米的51%,故此题错误;
D.要表示各部分数量与总数之间的关系,应选扇形统计图,故此题错误。
故选:A
【点睛】
此题考查的是基础知识的应用,熟练掌握基础知识是解题关键。
13.A
解析:A
【解析】
假设两根绳子的长度等于1米,大于1米,小于1米(大于米)时的长度,分别计算剩下部分的长度并比较大小即可。
情况1:假设两根绳子的长度为1米。
第一根绳子剩下的长度:1-=(米)
第二根绳子剩下的长度:1×(1-)=(米)
则两根绳子剩下的长度相等。
情况2:假设两根绳子的长度为2米。
第一根绳子剩下的长度:2-=(米)
第二根绳子剩下的长度:2×(1-)=(米)
米>米,则第一根绳子剩下的长度长。
情况3:假设两根绳子的长度为米。
第一根绳子剩下的长度:-=(米)
第二根绳子剩下的长度:×(1-)=(米)
米<米,则第二根绳子剩下的长度长。
所以两根绳子剩下的长度无法比较。
故答案为:A
【点睛】
题目中第一个是具体的量,第二个是分率,绳子的长度不确定时剩下的长度无法比较。
14.B
解析:B
【解析】
根据男生人数比女生人数多20%,女生人数是单位“1”,则男生人数占女生人数的1+20%,全班人数占女生人数的1+1+20%,求女生人数占全班的几分之几,用1÷全班对应百分率即可。
1÷(1+1+20%)
=1÷2.2
=
故答案为:B
【点睛】
关键是理解百分数的意义,此类问题一般用表示单位“1”的量作除数。
15.C
解析:C
【解析】
本题可先通过他们各自加工零件的个数及用时求出他们的工作效率,然后就能求出两者的效率比。
甲的工作效率为:3÷40=
乙的工作效率为:4÷30=
甲乙工作效率的比为∶=9∶16
故答案为:C
【点睛】
结果是比的问题一般要将结果根据比的基本性质化为最简整数比。
16.A
解析:A
【解析】
由倒数的定义可知,两个数乘积是1的数互为倒数。据此判断即可。
A.和7,,符合题意;
B.和,,不符合题意;
C.1和,,,不符合题意;
D.和0.5,,不符合题意;
故答案为:A
【点睛】
此题的解题关键是掌握倒数的概念和特点,得出正确的选项。
17.D
解析:D
【解析】
根据圆的面积公式:S=πr2,可得圆的面积比等于半径的平方比;也可以根据半径比3∶5,假设甲、乙两个圆的半径,根据比例尺求出两个圆的实际半径比,再用圆的面积公式求出面积比,据此解答。
3×3=9
5×5=25
所以这两个圆的实际面积比是9∶25。
故答案为:D
【点睛】
解答此题的关键是理解图上距离、实际距离、和比例尺的关系,以及圆的面积公式。
18.D
解析:D
【解析】
因为欢欢邮票张数的和乐乐邮票张数的相等,所以欢欢邮票张数×=乐乐邮票张数×,再逆用比例的基本性质作答,即在比例里,两个外项的积等于两个内项的积求出欢欢和乐乐邮票张数的比。
因为欢欢邮票张数×=乐乐邮票张数×
所以欢欢邮票张数∶乐乐邮票张数=∶=25∶28
故答案为:D
【点睛】
本题主要是根据题意得出数量关系式,再灵活利用比例的基本性质解决问题。
19.D
解析:D
【解析】
假设小正方形边长为1,求出整个长方形和阴影部分三角形的面积,阴影部分占整个长方形面积的分率=阴影部分的面积÷整个长方形的面积,结果化为最简分数,据此解答。
阴影部分的面积:4×1÷2=2
长方形的面积:5×1=5
2÷5=
故答案为:D
【点睛】
A占B的几分之几的计算方法:A÷B=,结果化为最简分数。
三、解答题
20.C
解析:C
【解析】
如图:
由A的位置到A1的位置时,所经过的路程是半径为4厘米的圆周长的,点A1的位置沿虚线到A2的位置时所经过的路程也是半径为5厘米的圆周长的,两次的路程之和就是顶点滚动经过的路线全长。
×3.14×2×4+×3.14×2×5
=6.28+7.85
=14.13(厘米)
故答案为:C
【点睛】
此题是考查图形的旋转、圆周长的计算等。图形旋转要注意四要素:即原位置、旋转中心、旋转方向、旋转角;圆的周长要弄清圆的半径。
21.B
解析:B
【解析】
由图可知,第1个图形每行1根小棒,一共2行,竖着每列有1根小棒,一共2列,一共有(2×2)根小棒;第2个图形横着每行有2根小棒,一共3行,竖着每列有2根小棒,一共有3列,一共有(2×3+3×2);第3个图形横着每行有3根小棒,一共4行,竖着每列有3根小棒,一共有4列,一共有(3×4+4×3)……第n个图形一共有n(n+1)+ n(n+1),化简计算当n=6时式子的值,据此解答。
分析可知,第n个图形小棒的总根数为:n(n+1)+ n(n+1)=2n(n+1)根
当n=6时,2n(n+1)=2×6×(6+1)=2×6×7=12×7=84(根)
所以,第6个图形一共有84根小棒。
故答案为:B
【点睛】
找出图形个数与小棒根数变化的规律是解答题目的关键。
21、;0;;;
0.2;200;5;93
【解析】
22、29;40
1.37;
【解析】
(1)运用乘法分配律进行简算;
(2)运用乘法分配律进行简算;
(3)运用减法性质进行简算;
(4)先算小括号里的减法,再算中括号里的减法,最后算括号外的乘法。
24×(+)
=24×+24×
=9+20
=29;
61×40%+38×+0.4
=(61+38+1)×40%
=100×40%
=40;
5.37-1.47-2.53
=5.37-(1.47+2.53)
=5.37-4
=1.37;
[1-(-)]×
=[1-]×
=×
=
23、;x=28;
【解析】
解:
解:
x=28
解:
24、75cm2;7.125平方厘米
【解析】
第一幅图,两个扇形可以拼成一个半圆,阴影部分的面积=长方形面积-半圆面积;
第二幅图,阴影部分的面积=圆的面积-正方形面积,其中正方形面积可以用对角线的平方÷2进行计算。
5×2×5-3.14×5 ÷2
=50-39.25
=10.75(平方厘米)
3.14×(5÷2) -5×5÷2
=3.14×6.25-12.5
=19.625-12.5
=7.125(平方厘米)
26.48页
【解析】
根据题意先把这本书的总页数看是单位“1”,则第一天读了全书的,就还剩下全书的(1-)用乘法可求出剩下的页数,再把剩下的页数看是单位“1”,第二天读了余下的,用乘法可求出第二天读的页
解析:48页
【解析】
根据题意先把这本书的总页数看是单位“1”,则第一天读了全书的,就还剩下全书的(1-)用乘法可求出剩下的页数,再把剩下的页数看是单位“1”,第二天读了余下的,用乘法可求出第二天读的页数,据此解答。
160×(1-)×
=160××
=48(页)
答:第二周读了48页。
【点睛】
此题考查的是分数乘法的应用,解答此题关键是依据分数乘法的意义,注意两次单位“1”的不同。
27.500千米/时
【解析】
磁悬浮列车的运行速度比超音速飞机的飞行速度少,把超音速飞机的飞行速度看作单位“1”, 磁悬浮列车的速度是它的(1-),用超音速飞机的飞行速度乘这个分率,可求出磁悬浮列车的运
解析:500千米/时
【解析】
磁悬浮列车的运行速度比超音速飞机的飞行速度少,把超音速飞机的飞行速度看作单位“1”, 磁悬浮列车的速度是它的(1-),用超音速飞机的飞行速度乘这个分率,可求出磁悬浮列车的运行速度。
磁悬浮列车的速度:
1500×(1-)
=1500×
=500(千米/时)
答:磁悬浮列车的速度是500千米/时。
【点睛】
找准单位“1”的量是解此题的关键。
28.28分
【解析】
长方形内最大的三角形等于长方形面积的一半,这样的三角形一定有一条边与长方形的某条边重合,且另一个顶点恰好在该长方形的对边上。所以只要讨论三人中有两个人在长方形的顶点上的情况,因为长
解析:28分
【解析】
长方形内最大的三角形等于长方形面积的一半,这样的三角形一定有一条边与长方形的某条边重合,且另一个顶点恰好在该长方形的对边上。所以只要讨论三人中有两个人在长方形的顶点上的情况,因为长方形的长AD与宽AB的比为5∶3,所以将长方形的长5等份,宽3等份,将其周长分为16段,又因为甲、乙、丙三人的速度比为4∶3∶5,所以他们所行的路程比也是4∶3∶5,设甲走4段用1个单位时间,那么一个单位时间内乙、丙分别走3段、5段,由于4、3、5两两互质,所以在非整数单位时间内甲、乙、丙三人最多有一人走了整数段,所以只考虑整数单位时间。然后对到达顶点的情况一一列举即可,得到满足条件的单位时间点,再根据第一次构成长方形中最大的三角形的时间是12分钟,从而求出一个单位时间相当于多少分钟,根据列表知道第二次构成最大三角形需要几个时间单位,求出再过多少分钟,三人所在位置的点的连线第二次构成最大三角形,据此解答。
根据分析将长方形的长为5等份,宽为3等份,那么长方形的周长为16段,设甲走4段用1个单位时间,那么一个单位时间内乙、丙分别走3段、5段,根据分析又知道只有整数单位时间才符合题意,所以只考虑整数单位时间,所以三人到达顶点的情况列表如下:
甲 单位时间 2 4 6 8 10 12 14 16 ……
地点 C A C A C A C C ……
乙 单位时间 2 3 10 11 18 19 26 27 ……
地点 D C B A D C B A ……
丙 单位时间 2 3 10 11 18 19 26 27 ……
地点 C B A D C B A D ……
通过列表可知2个单位时间时,甲和丙重合,不满足条件,3个单位时间时,甲在AD上,三人第一次构成最大的三角形,所以一个单位时间为12÷3=4(分);
10个单位时间的时候甲、乙、丙分别在C、B、A点上,第二次构成最大的三角形,
4×10-12
=40-12
=28(分)
答:再过28分钟,三人所在位置的点的连线第二次构成最大三角形。
【点睛】
此题考查的是行程问题,解题的关键是理解长方形内最大的三角形等于长方形面积的一半。
29.上层200本,下层250本
【解析】
解:设上层书架原有x本书,则下层书架原有(450﹣x)本,得
(1+)x=(450﹣x)×(1+)
x=(450﹣x)×
x=585﹣x
x=585
x=200
解析:上层200本,下层250本
【解析】
解:设上层书架原有x本书,则下层书架原有(450﹣x)本,得
(1+)x=(450﹣x)×(1+)
x=(450﹣x)×
x=585﹣x
x=585
x=200
450﹣200=250(本)
答:原来上层书架有图书200本、下层书架有图书250本.
30.(1)苹果;
(2)200人
【解析】
(1)扇形统计图中哪种水果所占的面积最大,最爱吃该种水果的可能性最大;
(2)把五年级学生总人数看作单位“1”,最爱吃香蕉和葡萄的同学占总人数的(23%+16
解析:(1)苹果;
(2)200人
【解析】
(1)扇形统计图中哪种水果所占的面积最大,最爱吃该种水果的可能性最大;
(2)把五年级学生总人数看作单位“1”,最爱吃香蕉和葡萄的同学占总人数的(23%+16%),根据“量÷对应的分率”求出五年级的总人数。
(1)分析可知,如果从五年级学生中随意抽取一人,这人最爱吃的水果是苹果的可能性最大。
(2)78÷(23%+16%)
=78÷0.39
=200(人)
答:五年级一共有学生200人。
【点睛】
已知一个数的百分之几是多少,求这个数用除法计算。
31.4升
【解析】
把这瓶洗衣液原有的升数看作单位“1”, 第一周用了总量的,第二周用了总量的20%,还剩下(1--20%),还剩下的2.2升,用“剩下的体积÷对应的分率”用除法计算即可。
2.2÷(1
解析:4升
【解析】
把这瓶洗衣液原有的升数看作单位“1”, 第一周用了总量的,第二周用了总量的20%,还剩下(1--20%),还剩下的2.2升,用“剩下的体积÷对应的分率”用除法计算即可。
2.2÷(1--20%)
=2.2÷(1-0.25-0.2)
=2.2÷0.55
=4(升)
答:这瓶洗衣液原有4升。
【点睛】
本题考查了分数、百分数复合应用题,关键是确定单位“1”,找到部分对应分率。
32.108千克
【解析】
把总质量看作单位“1”,用+45%+30%-1=求得梨所占总重量,进而求得苹果所占分率是-=,桃所占分率是45%-=,再用桃比苹果多42千克除以对应分率-求出总重量,再乘30%
解析:108千克
【解析】
把总质量看作单位“1”,用+45%+30%-1=求得梨所占总重量,进而求得苹果所占分率是-=,桃所占分率是45%-=,再用桃比苹果多42千克除以对应分率-求出总重量,再乘30%即可得到答案。
梨:+45%+30%-1
=-1
=
苹果:-=
桃:45%-=
42÷(-)
=42÷
=360(千克)
360×30%=108(千克)
答:枣有108千克。
【点睛】
此题考查的是分数、百分数应用,解答此题关键是找准单位“1”,明确数量间关系,列式解决问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
