青岛版淄博市六年级上册数学期末经典题目练习卷2(含答案)
文档属性
| 名称 | 青岛版淄博市六年级上册数学期末经典题目练习卷2(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 15:52:24 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
淄博市六年级上册数学期末试卷训练经典题目(含答案)
一、填空题
1、在括号里填上合适的单位。
(1)数学书的封面大约300( )。
(2)汽车油箱能容汽油20( )。
(3)一块橡皮的体积为7( )。
(4)小华身高135( )。
2、2÷5===6∶( )= ( )%=( )(小数)。
3、一根丝带长米,剪去米,还剩______米;如果剪去它的,那么还剩______米。
4、一台收割机小时收割小麦公顷。照这样计算,这台收割机1小时收割小麦( )公顷,收割2公顷小麦需要( )小时。
5、把一个圆平分成若干等分再拼成近似的长方形,如下图,阴影部分的面积是67.2cm2,圆的面积是( )cm2.
6、学校独轮车社团中,男、女生的人数比是8∶5。男生人数比女生人数多,女生人数比男生人数少( )%。
7、◎+☆=48,◎=☆十☆十☆,◎=( ),☆=( )。
8、笔记本的单价是练习本的5倍。买4本笔记本的钱可以买( )本练习本。
9、在一块长10分米,宽4分米的长方形铁板上,最多能截取( )个直径是2分米的圆形铁板。
10、如图,用同样长的小木棒摆一摆,照这样摆下去,第6幅图需要______根这样的小木棒,第n幅图需要______根这样的小木棒。
二、选择题
11、从12时到12时15分,分针转过的角度是( )。
A.90° B.180° C.360° D.15°
12、已知a、b、c是三个不等于0的数,并且,则a、b、c这三个数中最小的是( )。
A.a B.b C.c D.不能确定
13、下面3幅图中各摆了一些围棋棋子,其中黑色棋子的数量占该图中棋子总数的25%的是( )。
A. B. C.
14、在中,如果前项加上9,要使比值不变,后项应( )。
A.加上9 B.乘9 C.加上6
15、用一根长64厘米的铁丝围成下面三个图形,面积最大的是( )。
A.圆 B.长方形 C.正方形
16、在一个比例里,两个内项互为倒数。一个外项是,另一个外项是( )。
A.25 B.5 C.
17、圆锥和圆柱底面积相等,体积的比是1∶4,如果圆锥的高是2.4厘米,那么圆柱高是( )。
A.9.6厘米 B.3.2厘米 C.0.6厘米 D.4.2厘米
18、如图中阴影部分的面积占整个大长方形面积的( )。
A. B. C. D.
三、解答题
19、地球可以看作是一个近似圆的球体,假如地球平均半径是,则在离地球表面高度10米处的与地球是同心圆的周长比地球周长多( )。(π取3.14)
A.62.8 B.628 C.0.628 D.0.0628
20、下边图形周长的计算方法是( )。
A. B. C. D.
21、直接写出得数。
40%÷40%=
22、脱式计算,用自己喜欢的方法计算。
25.39-(5.39+9.1) (+-)÷
×[(-)÷0.5] -×0.75+÷
23、解方程。
x-20%x=9.6
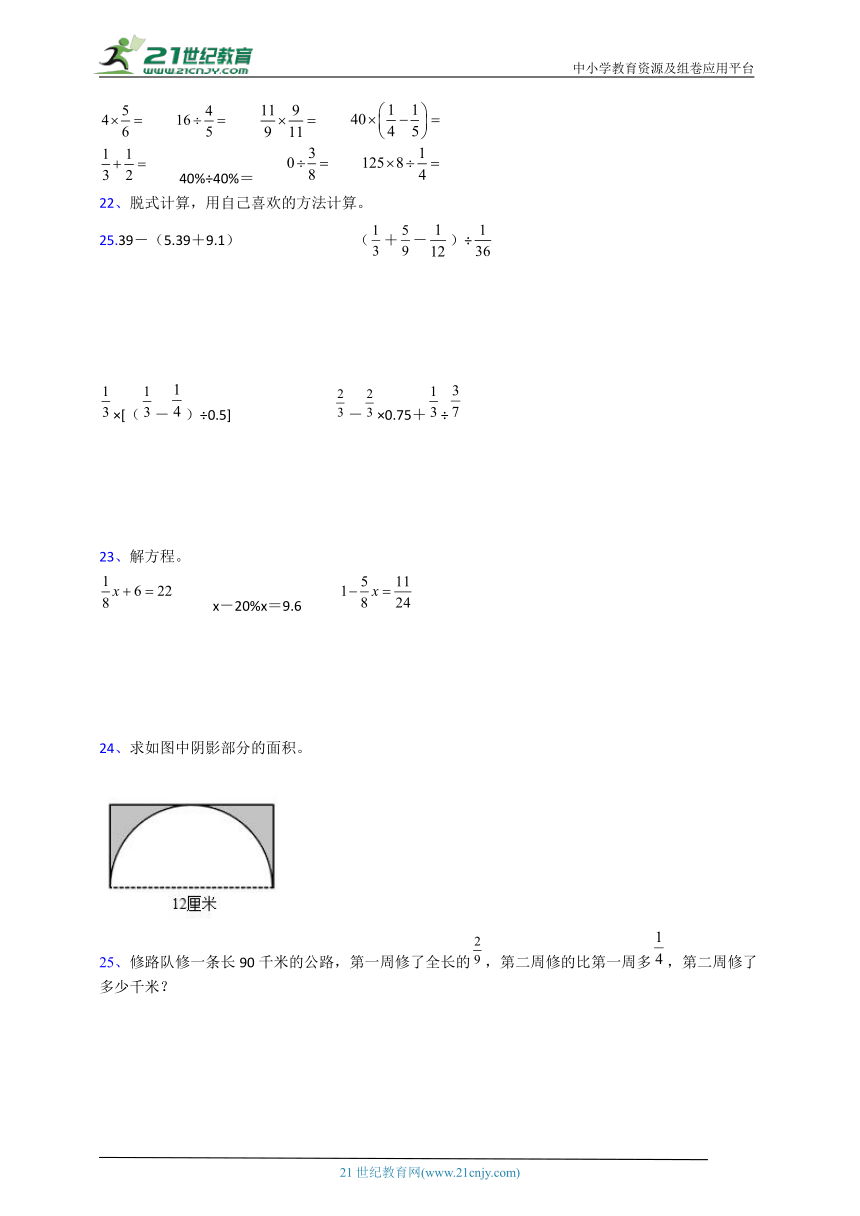
24、求如图中阴影部分的面积。
25、修路队修一条长90千米的公路,第一周修了全长的,第二周修的比第一周多,第二周修了多少千米?
26、学校果园有梨树75棵,桃树比梨树多。梨树和桃树一共有多少棵?
27.仙居目前的居民用电电价是0.55元/千瓦时。为了倡导建设“节约型社会”,鼓励市民安装分时电表实行峰谷时谷电价,具体收费标准如下:
时段 峰时(8:00~22:00) 谷时(22:00~次日8:00)
每千瓦时电价(元) 0.63 0.43
孔强家一年用电4800千瓦时,其中峰时用电量与谷时用电量的比是,如果孔强家安装分时电表,一年能节约多少钱?
28、某项工程,甲单独做需要30天完成,乙单独做需要20天完成。现在由甲、乙两队合作,中途甲队退出,余下的工程由乙队又做了5天才完成任务。如果做完这项工程共得工程款9000元,问甲队能得工程款多少元?
29、下面是某校六年级学生去年体育达标情况如图:
(1)完成下面的统计表。
项目 优秀 良好 达标 未达标
人数 60
(2)良好的人数比优秀的人数多百分之几?
30、某公司计划进一批原材料,原来每吨的价格是200元,现在每吨的价格上涨了25%。原计划进100吨原材料的钱,现在只能进多少吨?
31、如图,第二个图形是由第一个图形连接三边中点而得到的,第三个图形是由第二个图形中间的一个三角形连接三边中点而得到的,以此类推……分别写出第二个图形、第三个图形和第四个图形中的三角形个数.如果第n个图形中的三角形个数为8057,n是多少?
【参考答案】
一、填空题
1、 平方厘米 升 立方厘米 厘米
【解析】
根据生活经验、对面积单位、容积单位、体积单位、长度单位和数据大小,选择适当的计量单位填空即可。
(1)数学书的封面大约300平方厘米。
(2)汽车油箱能容汽油20升。
(3)一块橡皮的体积为7立方厘米。
(4)小华身高135厘米。
【点睛】
此题考查了根据情景选择合适的计量单位,根据生活经验、对每种单位和数据大小的认识,即可做出选择。
2、10;30;15;40;0.4
【解析】
根据除法与分数的关系把2÷5写成分数形式,再根据分数的基本性质:分数的分子和分母同时乘或除以一个相同的数(0除外),分数大小不变,以及分数与比、百分数、小数的关系进行转化。
2÷5==
2÷5==
2÷5=2∶5=(2×3)∶(5×3)=6∶15
2÷5=0.4=40%
所以2÷5===6∶15=40%=0.4
【点睛】
此题考查的是分数与比、百分数、小数的关系,掌握它们间的关系是解题关键。
3、
【解析】
还剩的米数=丝带全长-剪去的长度;把全长看作单位“1”,则还剩下全长的(1-),全长×还剩的所占全长分率即可。
-=(米)
剪去米,还剩米;
×(1-)
=×
=(米)
如果剪去它的,那么还剩米。
【点睛】
此题考查了异分母分数加减法以及分数混合运算,注意分数带单位和不带单位表示的意义是不同的。
4、
【解析】
根据工作效率=工作总量÷时间,代入数据解答即可;用2÷求出2公顷中含有几个公顷,再乘即可。
÷=(公顷),1小时收割小麦公顷。
2÷×
=2× ×
=(小时),收割2公顷小麦需要小时。
【点睛】
掌握工作总量、工作效率和工作时间关系,以及分数乘除法的计算法则,认真计算即可。
5、6
【解析】
6、;37.5
【解析】
求男生人数比女生人数多几分之几,用男女生人数所占份数之差除以女生所占份数即可;求女生人数比男生人数少百分之几,用男女生人数所占份数之差除以男生人数所占份数乘100%即可。
(8-5)÷5
=3÷5
= ,男生人数比女生人数多;
(8-5)÷8×100%
=3÷8×100%
=37.5%,女生人数比男生人数少37.5%。
【点睛】
此题考查了求一个数比另一个数多(少)几分之几(百分之几),注意两次运算除数的变化。
7、 36 12
【解析】
由于◎+☆=48,◎=☆十☆十☆,则☆=48÷4=12, ◎是3个☆相加,则一个◎:12×3=36
☆=48÷(1+3)=48÷4=12
◎=12×3=36
【点睛】
正确理解等量代还的意义,是解答此题的关键。
8、20
【解析】
根据题意,笔记本的单价是练习本的5倍,即1本笔记本价钱=5本练习本价钱;4本笔记本的价钱是多少本练习本的价钱,用4×5,即可解答。
4×5=20(本)
【点睛】
本题考查等量代换,利用1本笔记本价钱=5本练习本的价钱,进行解答。
9、10
【解析】
先分别计算出在长方形铁板的长和宽上,各能截取多少个2分米,再将得到的值相乘,就是能截取的直径为2分米的圆形铁板的个数。
10÷2=5
4÷2=2
5×2=10(个)
则最多能截取10个直径是2分米的圆形铁板。
【点睛】
解答此题的关键是,分别计算出在长方形铁板的长和宽上各含有多少个2分米,从而可以求得截取的直径为2分米的圆形铁板的个数。
10、 34 (6n-2)
【解析】
第1幅图需要4根小木棒,4=6×1-2;
第2幅图需要10根小木棒,10=6×2-2;
第3幅图需要16根小木棒,16=6×3-2;
……
第n幅图需要的小木棒数:(6n-2)根。
第6幅图需要小木棒:
6×6-2
=36-2
=34(根)
第n幅图需要的小木棒数为(6n-2)根。
【点睛】
本题主要考查数与形结合的规律,发现每多1个图形就多6根小棒是解题的关键。
二、选择题
12.A
解析:A
【解析】
钟表上有12大格,每两个数字之间对应的圆心角是360°÷12=30°。从12时到12时15分,分针从12走到3,走了3大格,转过的角度是30°×3=90°。
通过分析可知,从12时到12时15分,分针转过的角度是90°。
故答案为:A
【点睛】
明确“钟表上分针和时针每走一大格,转过的角度是30°”是解题的关键。
13.B
解析:B
【解析】
设a×=b÷25%=c×=1,分别求出a、b、c的值,再比较大小即可。
设a×=b÷25%=c×=1
a×=1
a=1÷
a=1×
a=
b÷25%=1
b=1×25%
b=
c×=1
c=1÷
c=1×
c=
a==;b==;c==
a>c>b
故答案为:B
【点睛】
利用分数除法、百分数与分数的互化、异分母分数比较大小的方法进行解答。
14.B
解析:B
【解析】
因为每幅图中都是20个棋子,把棋子的总数看作单位“1”,根据一个数乘百分数的意义,用乘法求出它的25%,也就是黑棋子的个数;由此进行选择即可。
(个)
即黑棋子的个数是5个,符合题意的只有选项B。
故答案为:B
【点睛】
判断出单位“1”,根据一个数乘百分数的意义,用乘法求出黑棋子的个数,是解答此题的关键。
15.C
解析:C
【解析】
根据比的基本性质:比的前项和后项同时乘或除以一个相同的数(0除外),比值不变,据此解答。
(3+9)÷3
=12÷3
=4
2×4-2
=8-2
=6
故答案为:C
【点睛】
利用比的基本性质进行解答。
16.A
解析:A
【解析】
我们可以进行举例,假设围成了长方形、正方形、及圆等平面图形,分别求出面积再进行比较,进行判断。
正方形的面积:64÷4=16(厘米)
16×16=256(平方厘米)
长方形的面积:64÷2=32(厘米)
32=15+17
15×17=255(平方厘米)
圆的面积:64÷2÷3.14
=32÷3.14
≈10(厘米)
3.14×102
=3.14×100
=314(平方厘米)
314>256>255
所以圆的面积>正方形的面积>长方形的面积,
因此,围成圆时面积最大
故答案为:A
【点睛】
本题考查长方形、正方形及圆的面积公式的掌握及运用情况,考查了学生的分析、解决问题的能力。
17.B
解析:B
【解析】
根据比例的基本性质,两内项之积等于两外项之积,如果两个内项互为倒数,也就是乘积为1,那么两外项的乘积也是1,1除以即为另一个内项。
1÷=5
故答案为:B
【点睛】
本题考查的是比例的基本性质和倒数的意义,两个内项互为倒数,那么两个外项也互为倒数。
18.B
解析:B
【解析】
根据圆柱的体积公式:底面积×高;圆锥的体积公式:底面积×高×;设圆柱的底面积为s,则圆锥的底面积也为s,圆柱的高为h,再根据圆锥体积比圆柱的体积是1∶4,求出圆柱的高。
设圆锥的底面积为s,则圆柱的底面积也是s,设圆柱的高为h
圆锥的体积:s×2.4×
圆柱的体积:s×h
2.4×s∶sh=1∶4
0.8∶h=1∶4
h=0.8×4
h=3.2
故答案选:B
【点睛】
本题考查圆柱、圆锥的体积公式的应用。
19.C
解析:C
【解析】
由图可知,阴影部分的两个三角形等底等高,所以面积相等,假设每个小正方形的面积是1,用阴影部分的面积除以整个大长方形面积即可。
(1×1÷2×2)÷(4×1)
=1÷4
=
故答案为:C。
【点睛】
明确阴影部分两个三角形的关系是解答本题的关键。
三、解答题
20.D
解析:D
【解析】
圆的周长公式为,题目的意思是计算两个圆的周长差,可以直接利用半径差进行求解,,无需计算各自的周长。
62.8米=0.0628千米
故答案选D。
【点睛】
半径决定圆的大小,知道半径差就可以求出周长差,不需要计算具体的周长,另外注意单位换算。
21.C
解析:C
【解析】
根据半圆周长=圆周长的一半+直径,进行分析。
这个半圆周长=。
故答案为:C
【点睛】
关键是掌握半圆周长求法,半圆周长=πr+2r。
21、;20;1;2
;1;0;4000
【解析】
22、9;29;
;
【解析】
(1)小括号打开,加号变减号,先计算25.39-5.39,再计算另一个减法;
(2)除以变成乘36,利用乘法分配律简便计算;
(3)先计算小括号里的分数减法,再计算除法,最后计算中括号外的乘法;
(4)先计算-×0.75,提取相同的分数,利用乘法分配律简便计算,同时计算出后面的分数除法,最后计算加法。
25.39-(5.39+9.1)
=25.39-5.39-9.1
=20-9.1
=10.9
(+-)÷
=(+-)×36
=×36+×36-×36
=12+20-3
=29
×[(-)÷0.5]
=×[(-)÷]
=×[÷]
=×
=
-×0.75+÷
=×(1-0.75)+
=×+
=+
=+
=
23、x=128;x=12;x=
【解析】
①可以把看成一个整体,应用等式的性质1,方程左右两边同时减去6,再应用等式性质2,方程左右两边同时除以,得到方程的解;
②逆用乘法分配律,百分数化为小数,将方程整理成0.8x=9.6,最后应用等式的性质2,方程左右两边同时除以0.8,得到方程的解;
③含有未知数的项作为减数,可应用减法中各部分的关系,将方程整理成,最后应用等式的性质2,将方程左右两边同时除以,得到方程的解。
解:
x-20%x=9.6
解:(1-0.2)x=9.6
0.8x=9.6
x=9.6÷0.8
x=12
解:
24、48平方厘米
【解析】
观察图形可得:阴影部分的面积长方形面积半圆的面积,长方形的长是12厘米,宽是厘米,圆的直径是12厘米,然后再根据长方形的面积公式,圆的面积公式进行解答。
12×(12÷2)-3.14×(12÷2)2÷2
=12×6-3.14×36÷2
=72-3.14×18
=72-56.52
=15.48(平方厘米)
26.25千米
【解析】
把全长90千米看成单位“1”,根据求一个数的几分之几是多少用乘法求出第一周修的长度,再把第一周修的长度看作单位“1”,第二周修的是1+,单位“1”已知用乘法计算即可。
90××(
解析:25千米
【解析】
把全长90千米看成单位“1”,根据求一个数的几分之几是多少用乘法求出第一周修的长度,再把第一周修的长度看作单位“1”,第二周修的是1+,单位“1”已知用乘法计算即可。
90××(1+)
=20×
=25(千米)
答:第二周修了25千米。
【点睛】
此题考查的是分数乘法的应用,解答此题应注意单位“1”的不同。
27.180棵
【解析】
把梨树的棵数看作单位“1”,单位“1”已知,用乘法,桃树相当于梨树的(1+),用梨树的棵数乘(1+)计算出桃树的棵数,再加上梨树的棵数即可得解。
75+75×(1+)
=75+7
解析:180棵
【解析】
把梨树的棵数看作单位“1”,单位“1”已知,用乘法,桃树相当于梨树的(1+),用梨树的棵数乘(1+)计算出桃树的棵数,再加上梨树的棵数即可得解。
75+75×(1+)
=75+75×
=75+105
=180(棵)
答:梨树和桃树一共有180棵。
【点睛】
此题的解题关键是根据单位“1”的确定,按照求比一个数多几分之几的数是多少的方法,求出桃树的棵数,最终求出两种树的和。
28.176元
【解析】
根据单价×数量=总价,求出孔强家安装分时电表的费用;根据比的意义,用总用电量÷峰时和谷时用电量总份数,求出一份数对应用电量,一份数用电量分别乘峰时和谷时对应份数,求出峰时和谷时用
解析:176元
【解析】
根据单价×数量=总价,求出孔强家安装分时电表的费用;根据比的意义,用总用电量÷峰时和谷时用电量总份数,求出一份数对应用电量,一份数用电量分别乘峰时和谷时对应份数,求出峰时和谷时用电量,峰时用电量×单价+谷时用电量×单价=安装分时电表总费用,再求出安装前和安装后的费用差即可。
4800×0.55=2640(元)
4800÷(5+7)
=4800÷12
=400(千瓦时)
400×5=2000(千瓦时)
400×7=2800(千瓦时)
2000×0.63+2800×0.43
=1260+1204
=2464(元)
2640-2464=176(元)
答:装分时电表,一年能节约176元钱。
【点睛】
关键是理解比的意义,按比例分配应用题关键是先求出一份数。
29.2700元
【解析】
由题意可知,把这项工程看作单位“1”,甲单独做每天完成这项工程的,乙单独做每天完成这项工程的,乙队单独做了5天,完成了这项工程的×5=,由甲、乙两队合作完成的占总工程的1-=,
解析:2700元
【解析】
由题意可知,把这项工程看作单位“1”,甲单独做每天完成这项工程的,乙单独做每天完成这项工程的,乙队单独做了5天,完成了这项工程的×5=,由甲、乙两队合作完成的占总工程的1-=,合作的天数=÷(+)=9(天);甲队完成的工作量是:×9=,则甲也应得工程款的,用9000×;据此解答。
甲乙合作的天数:
(1-×5)÷(+)
=(1-)÷
=×12
=9(天)
甲队完成的工作量:×9=
甲应得工程款:9000×=2700(元)
答:甲队能得工程款2700元。
【点睛】
本题体现了数量关系式:工效之和×合作时间=工作总量;解答此题的关键是理解甲队完成了工作总量的几分之几,他应得的工程款也是总工程款的几分之几。
30.(1)40;70;30;(2)50%
【解析】
(1)良好的人数有60人,占总人数的30%,所以总人数有60÷30%=200(人)。用总人数分别乘20%、35%,求出优秀人数和达标人数,最后用总人数
解析:(1)40;70;30;(2)50%
【解析】
(1)良好的人数有60人,占总人数的30%,所以总人数有60÷30%=200(人)。用总人数分别乘20%、35%,求出优秀人数和达标人数,最后用总人数减去优秀人数、良好人数和达标人数,求出未达标的人数,从而填表。
(2)用良好的人数减去优秀的人数,再将差除以优秀的人数,求出良好的人数比优秀的人数多百分之几。
(1)总人数:60÷30%=200(人)
优秀人数:200×20%=40(人)
达标人数:200×35%=70(人)
未达标人数:200-40-60-70=30(人)
填表如下:
项目 优秀 良好 达标 未达标
人数 40 60 70 30
(2)(60-40)÷40×100%
=20÷40×100%
=50%
答:良好的人数比优秀的人数多50%。
【点睛】
本题考查了扇形统计图的应用,能根据扇形统计图获取有用信息是解题的关键。
31.80吨
【解析】
把原来每吨原材料的价格看作单位“1”,现在每吨原材料的价格=原来每吨原材料的价格×(1+25%),根据“总价=单价×数量”求出原来进100吨原材料需要的钱数,现在可以进的吨数=原来
解析:80吨
【解析】
把原来每吨原材料的价格看作单位“1”,现在每吨原材料的价格=原来每吨原材料的价格×(1+25%),根据“总价=单价×数量”求出原来进100吨原材料需要的钱数,现在可以进的吨数=原来进100吨原材料需要的钱数÷现在每吨原材料的价格,据此解答。
100×200÷[200×(1+25%)]
=100×200÷[200×1.25]
=100×200÷250
=20000÷250
=80(吨)
答:现在只能进80吨。
【点睛】
掌握单价、总价、数量之间的关系是解答题目的关键。
32.解:第一个图形中三角形个数:1个;
第二个图形中三角形个数:1×4+1=5(个);
第三个图形中三角形个数:2×4+1=9(个);
第四个图形中三角形个数:3×4+1=13(个);
第n个图形中三角
解析:解:第一个图形中三角形个数:1个;
第二个图形中三角形个数:1×4+1=5(个);
第三个图形中三角形个数:2×4+1=9(个);
第四个图形中三角形个数:3×4+1=13(个);
第n个图形中三角形个数:
(n-1)×4+1=(4n-3)(个)
4n-3=8057,n=2015.
答:n是第2015个图形.
【解析】
由已知图形中三角形个数推出三角形个数与图形个数之间的数量关系式,再根据题意代入数据计算即可解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
淄博市六年级上册数学期末试卷训练经典题目(含答案)
一、填空题
1、在括号里填上合适的单位。
(1)数学书的封面大约300( )。
(2)汽车油箱能容汽油20( )。
(3)一块橡皮的体积为7( )。
(4)小华身高135( )。
2、2÷5===6∶( )= ( )%=( )(小数)。
3、一根丝带长米,剪去米,还剩______米;如果剪去它的,那么还剩______米。
4、一台收割机小时收割小麦公顷。照这样计算,这台收割机1小时收割小麦( )公顷,收割2公顷小麦需要( )小时。
5、把一个圆平分成若干等分再拼成近似的长方形,如下图,阴影部分的面积是67.2cm2,圆的面积是( )cm2.
6、学校独轮车社团中,男、女生的人数比是8∶5。男生人数比女生人数多,女生人数比男生人数少( )%。
7、◎+☆=48,◎=☆十☆十☆,◎=( ),☆=( )。
8、笔记本的单价是练习本的5倍。买4本笔记本的钱可以买( )本练习本。
9、在一块长10分米,宽4分米的长方形铁板上,最多能截取( )个直径是2分米的圆形铁板。
10、如图,用同样长的小木棒摆一摆,照这样摆下去,第6幅图需要______根这样的小木棒,第n幅图需要______根这样的小木棒。
二、选择题
11、从12时到12时15分,分针转过的角度是( )。
A.90° B.180° C.360° D.15°
12、已知a、b、c是三个不等于0的数,并且,则a、b、c这三个数中最小的是( )。
A.a B.b C.c D.不能确定
13、下面3幅图中各摆了一些围棋棋子,其中黑色棋子的数量占该图中棋子总数的25%的是( )。
A. B. C.
14、在中,如果前项加上9,要使比值不变,后项应( )。
A.加上9 B.乘9 C.加上6
15、用一根长64厘米的铁丝围成下面三个图形,面积最大的是( )。
A.圆 B.长方形 C.正方形
16、在一个比例里,两个内项互为倒数。一个外项是,另一个外项是( )。
A.25 B.5 C.
17、圆锥和圆柱底面积相等,体积的比是1∶4,如果圆锥的高是2.4厘米,那么圆柱高是( )。
A.9.6厘米 B.3.2厘米 C.0.6厘米 D.4.2厘米
18、如图中阴影部分的面积占整个大长方形面积的( )。
A. B. C. D.
三、解答题
19、地球可以看作是一个近似圆的球体,假如地球平均半径是,则在离地球表面高度10米处的与地球是同心圆的周长比地球周长多( )。(π取3.14)
A.62.8 B.628 C.0.628 D.0.0628
20、下边图形周长的计算方法是( )。
A. B. C. D.
21、直接写出得数。
40%÷40%=
22、脱式计算,用自己喜欢的方法计算。
25.39-(5.39+9.1) (+-)÷
×[(-)÷0.5] -×0.75+÷
23、解方程。
x-20%x=9.6
24、求如图中阴影部分的面积。
25、修路队修一条长90千米的公路,第一周修了全长的,第二周修的比第一周多,第二周修了多少千米?
26、学校果园有梨树75棵,桃树比梨树多。梨树和桃树一共有多少棵?
27.仙居目前的居民用电电价是0.55元/千瓦时。为了倡导建设“节约型社会”,鼓励市民安装分时电表实行峰谷时谷电价,具体收费标准如下:
时段 峰时(8:00~22:00) 谷时(22:00~次日8:00)
每千瓦时电价(元) 0.63 0.43
孔强家一年用电4800千瓦时,其中峰时用电量与谷时用电量的比是,如果孔强家安装分时电表,一年能节约多少钱?
28、某项工程,甲单独做需要30天完成,乙单独做需要20天完成。现在由甲、乙两队合作,中途甲队退出,余下的工程由乙队又做了5天才完成任务。如果做完这项工程共得工程款9000元,问甲队能得工程款多少元?
29、下面是某校六年级学生去年体育达标情况如图:
(1)完成下面的统计表。
项目 优秀 良好 达标 未达标
人数 60
(2)良好的人数比优秀的人数多百分之几?
30、某公司计划进一批原材料,原来每吨的价格是200元,现在每吨的价格上涨了25%。原计划进100吨原材料的钱,现在只能进多少吨?
31、如图,第二个图形是由第一个图形连接三边中点而得到的,第三个图形是由第二个图形中间的一个三角形连接三边中点而得到的,以此类推……分别写出第二个图形、第三个图形和第四个图形中的三角形个数.如果第n个图形中的三角形个数为8057,n是多少?
【参考答案】
一、填空题
1、 平方厘米 升 立方厘米 厘米
【解析】
根据生活经验、对面积单位、容积单位、体积单位、长度单位和数据大小,选择适当的计量单位填空即可。
(1)数学书的封面大约300平方厘米。
(2)汽车油箱能容汽油20升。
(3)一块橡皮的体积为7立方厘米。
(4)小华身高135厘米。
【点睛】
此题考查了根据情景选择合适的计量单位,根据生活经验、对每种单位和数据大小的认识,即可做出选择。
2、10;30;15;40;0.4
【解析】
根据除法与分数的关系把2÷5写成分数形式,再根据分数的基本性质:分数的分子和分母同时乘或除以一个相同的数(0除外),分数大小不变,以及分数与比、百分数、小数的关系进行转化。
2÷5==
2÷5==
2÷5=2∶5=(2×3)∶(5×3)=6∶15
2÷5=0.4=40%
所以2÷5===6∶15=40%=0.4
【点睛】
此题考查的是分数与比、百分数、小数的关系,掌握它们间的关系是解题关键。
3、
【解析】
还剩的米数=丝带全长-剪去的长度;把全长看作单位“1”,则还剩下全长的(1-),全长×还剩的所占全长分率即可。
-=(米)
剪去米,还剩米;
×(1-)
=×
=(米)
如果剪去它的,那么还剩米。
【点睛】
此题考查了异分母分数加减法以及分数混合运算,注意分数带单位和不带单位表示的意义是不同的。
4、
【解析】
根据工作效率=工作总量÷时间,代入数据解答即可;用2÷求出2公顷中含有几个公顷,再乘即可。
÷=(公顷),1小时收割小麦公顷。
2÷×
=2× ×
=(小时),收割2公顷小麦需要小时。
【点睛】
掌握工作总量、工作效率和工作时间关系,以及分数乘除法的计算法则,认真计算即可。
5、6
【解析】
6、;37.5
【解析】
求男生人数比女生人数多几分之几,用男女生人数所占份数之差除以女生所占份数即可;求女生人数比男生人数少百分之几,用男女生人数所占份数之差除以男生人数所占份数乘100%即可。
(8-5)÷5
=3÷5
= ,男生人数比女生人数多;
(8-5)÷8×100%
=3÷8×100%
=37.5%,女生人数比男生人数少37.5%。
【点睛】
此题考查了求一个数比另一个数多(少)几分之几(百分之几),注意两次运算除数的变化。
7、 36 12
【解析】
由于◎+☆=48,◎=☆十☆十☆,则☆=48÷4=12, ◎是3个☆相加,则一个◎:12×3=36
☆=48÷(1+3)=48÷4=12
◎=12×3=36
【点睛】
正确理解等量代还的意义,是解答此题的关键。
8、20
【解析】
根据题意,笔记本的单价是练习本的5倍,即1本笔记本价钱=5本练习本价钱;4本笔记本的价钱是多少本练习本的价钱,用4×5,即可解答。
4×5=20(本)
【点睛】
本题考查等量代换,利用1本笔记本价钱=5本练习本的价钱,进行解答。
9、10
【解析】
先分别计算出在长方形铁板的长和宽上,各能截取多少个2分米,再将得到的值相乘,就是能截取的直径为2分米的圆形铁板的个数。
10÷2=5
4÷2=2
5×2=10(个)
则最多能截取10个直径是2分米的圆形铁板。
【点睛】
解答此题的关键是,分别计算出在长方形铁板的长和宽上各含有多少个2分米,从而可以求得截取的直径为2分米的圆形铁板的个数。
10、 34 (6n-2)
【解析】
第1幅图需要4根小木棒,4=6×1-2;
第2幅图需要10根小木棒,10=6×2-2;
第3幅图需要16根小木棒,16=6×3-2;
……
第n幅图需要的小木棒数:(6n-2)根。
第6幅图需要小木棒:
6×6-2
=36-2
=34(根)
第n幅图需要的小木棒数为(6n-2)根。
【点睛】
本题主要考查数与形结合的规律,发现每多1个图形就多6根小棒是解题的关键。
二、选择题
12.A
解析:A
【解析】
钟表上有12大格,每两个数字之间对应的圆心角是360°÷12=30°。从12时到12时15分,分针从12走到3,走了3大格,转过的角度是30°×3=90°。
通过分析可知,从12时到12时15分,分针转过的角度是90°。
故答案为:A
【点睛】
明确“钟表上分针和时针每走一大格,转过的角度是30°”是解题的关键。
13.B
解析:B
【解析】
设a×=b÷25%=c×=1,分别求出a、b、c的值,再比较大小即可。
设a×=b÷25%=c×=1
a×=1
a=1÷
a=1×
a=
b÷25%=1
b=1×25%
b=
c×=1
c=1÷
c=1×
c=
a==;b==;c==
a>c>b
故答案为:B
【点睛】
利用分数除法、百分数与分数的互化、异分母分数比较大小的方法进行解答。
14.B
解析:B
【解析】
因为每幅图中都是20个棋子,把棋子的总数看作单位“1”,根据一个数乘百分数的意义,用乘法求出它的25%,也就是黑棋子的个数;由此进行选择即可。
(个)
即黑棋子的个数是5个,符合题意的只有选项B。
故答案为:B
【点睛】
判断出单位“1”,根据一个数乘百分数的意义,用乘法求出黑棋子的个数,是解答此题的关键。
15.C
解析:C
【解析】
根据比的基本性质:比的前项和后项同时乘或除以一个相同的数(0除外),比值不变,据此解答。
(3+9)÷3
=12÷3
=4
2×4-2
=8-2
=6
故答案为:C
【点睛】
利用比的基本性质进行解答。
16.A
解析:A
【解析】
我们可以进行举例,假设围成了长方形、正方形、及圆等平面图形,分别求出面积再进行比较,进行判断。
正方形的面积:64÷4=16(厘米)
16×16=256(平方厘米)
长方形的面积:64÷2=32(厘米)
32=15+17
15×17=255(平方厘米)
圆的面积:64÷2÷3.14
=32÷3.14
≈10(厘米)
3.14×102
=3.14×100
=314(平方厘米)
314>256>255
所以圆的面积>正方形的面积>长方形的面积,
因此,围成圆时面积最大
故答案为:A
【点睛】
本题考查长方形、正方形及圆的面积公式的掌握及运用情况,考查了学生的分析、解决问题的能力。
17.B
解析:B
【解析】
根据比例的基本性质,两内项之积等于两外项之积,如果两个内项互为倒数,也就是乘积为1,那么两外项的乘积也是1,1除以即为另一个内项。
1÷=5
故答案为:B
【点睛】
本题考查的是比例的基本性质和倒数的意义,两个内项互为倒数,那么两个外项也互为倒数。
18.B
解析:B
【解析】
根据圆柱的体积公式:底面积×高;圆锥的体积公式:底面积×高×;设圆柱的底面积为s,则圆锥的底面积也为s,圆柱的高为h,再根据圆锥体积比圆柱的体积是1∶4,求出圆柱的高。
设圆锥的底面积为s,则圆柱的底面积也是s,设圆柱的高为h
圆锥的体积:s×2.4×
圆柱的体积:s×h
2.4×s∶sh=1∶4
0.8∶h=1∶4
h=0.8×4
h=3.2
故答案选:B
【点睛】
本题考查圆柱、圆锥的体积公式的应用。
19.C
解析:C
【解析】
由图可知,阴影部分的两个三角形等底等高,所以面积相等,假设每个小正方形的面积是1,用阴影部分的面积除以整个大长方形面积即可。
(1×1÷2×2)÷(4×1)
=1÷4
=
故答案为:C。
【点睛】
明确阴影部分两个三角形的关系是解答本题的关键。
三、解答题
20.D
解析:D
【解析】
圆的周长公式为,题目的意思是计算两个圆的周长差,可以直接利用半径差进行求解,,无需计算各自的周长。
62.8米=0.0628千米
故答案选D。
【点睛】
半径决定圆的大小,知道半径差就可以求出周长差,不需要计算具体的周长,另外注意单位换算。
21.C
解析:C
【解析】
根据半圆周长=圆周长的一半+直径,进行分析。
这个半圆周长=。
故答案为:C
【点睛】
关键是掌握半圆周长求法,半圆周长=πr+2r。
21、;20;1;2
;1;0;4000
【解析】
22、9;29;
;
【解析】
(1)小括号打开,加号变减号,先计算25.39-5.39,再计算另一个减法;
(2)除以变成乘36,利用乘法分配律简便计算;
(3)先计算小括号里的分数减法,再计算除法,最后计算中括号外的乘法;
(4)先计算-×0.75,提取相同的分数,利用乘法分配律简便计算,同时计算出后面的分数除法,最后计算加法。
25.39-(5.39+9.1)
=25.39-5.39-9.1
=20-9.1
=10.9
(+-)÷
=(+-)×36
=×36+×36-×36
=12+20-3
=29
×[(-)÷0.5]
=×[(-)÷]
=×[÷]
=×
=
-×0.75+÷
=×(1-0.75)+
=×+
=+
=+
=
23、x=128;x=12;x=
【解析】
①可以把看成一个整体,应用等式的性质1,方程左右两边同时减去6,再应用等式性质2,方程左右两边同时除以,得到方程的解;
②逆用乘法分配律,百分数化为小数,将方程整理成0.8x=9.6,最后应用等式的性质2,方程左右两边同时除以0.8,得到方程的解;
③含有未知数的项作为减数,可应用减法中各部分的关系,将方程整理成,最后应用等式的性质2,将方程左右两边同时除以,得到方程的解。
解:
x-20%x=9.6
解:(1-0.2)x=9.6
0.8x=9.6
x=9.6÷0.8
x=12
解:
24、48平方厘米
【解析】
观察图形可得:阴影部分的面积长方形面积半圆的面积,长方形的长是12厘米,宽是厘米,圆的直径是12厘米,然后再根据长方形的面积公式,圆的面积公式进行解答。
12×(12÷2)-3.14×(12÷2)2÷2
=12×6-3.14×36÷2
=72-3.14×18
=72-56.52
=15.48(平方厘米)
26.25千米
【解析】
把全长90千米看成单位“1”,根据求一个数的几分之几是多少用乘法求出第一周修的长度,再把第一周修的长度看作单位“1”,第二周修的是1+,单位“1”已知用乘法计算即可。
90××(
解析:25千米
【解析】
把全长90千米看成单位“1”,根据求一个数的几分之几是多少用乘法求出第一周修的长度,再把第一周修的长度看作单位“1”,第二周修的是1+,单位“1”已知用乘法计算即可。
90××(1+)
=20×
=25(千米)
答:第二周修了25千米。
【点睛】
此题考查的是分数乘法的应用,解答此题应注意单位“1”的不同。
27.180棵
【解析】
把梨树的棵数看作单位“1”,单位“1”已知,用乘法,桃树相当于梨树的(1+),用梨树的棵数乘(1+)计算出桃树的棵数,再加上梨树的棵数即可得解。
75+75×(1+)
=75+7
解析:180棵
【解析】
把梨树的棵数看作单位“1”,单位“1”已知,用乘法,桃树相当于梨树的(1+),用梨树的棵数乘(1+)计算出桃树的棵数,再加上梨树的棵数即可得解。
75+75×(1+)
=75+75×
=75+105
=180(棵)
答:梨树和桃树一共有180棵。
【点睛】
此题的解题关键是根据单位“1”的确定,按照求比一个数多几分之几的数是多少的方法,求出桃树的棵数,最终求出两种树的和。
28.176元
【解析】
根据单价×数量=总价,求出孔强家安装分时电表的费用;根据比的意义,用总用电量÷峰时和谷时用电量总份数,求出一份数对应用电量,一份数用电量分别乘峰时和谷时对应份数,求出峰时和谷时用
解析:176元
【解析】
根据单价×数量=总价,求出孔强家安装分时电表的费用;根据比的意义,用总用电量÷峰时和谷时用电量总份数,求出一份数对应用电量,一份数用电量分别乘峰时和谷时对应份数,求出峰时和谷时用电量,峰时用电量×单价+谷时用电量×单价=安装分时电表总费用,再求出安装前和安装后的费用差即可。
4800×0.55=2640(元)
4800÷(5+7)
=4800÷12
=400(千瓦时)
400×5=2000(千瓦时)
400×7=2800(千瓦时)
2000×0.63+2800×0.43
=1260+1204
=2464(元)
2640-2464=176(元)
答:装分时电表,一年能节约176元钱。
【点睛】
关键是理解比的意义,按比例分配应用题关键是先求出一份数。
29.2700元
【解析】
由题意可知,把这项工程看作单位“1”,甲单独做每天完成这项工程的,乙单独做每天完成这项工程的,乙队单独做了5天,完成了这项工程的×5=,由甲、乙两队合作完成的占总工程的1-=,
解析:2700元
【解析】
由题意可知,把这项工程看作单位“1”,甲单独做每天完成这项工程的,乙单独做每天完成这项工程的,乙队单独做了5天,完成了这项工程的×5=,由甲、乙两队合作完成的占总工程的1-=,合作的天数=÷(+)=9(天);甲队完成的工作量是:×9=,则甲也应得工程款的,用9000×;据此解答。
甲乙合作的天数:
(1-×5)÷(+)
=(1-)÷
=×12
=9(天)
甲队完成的工作量:×9=
甲应得工程款:9000×=2700(元)
答:甲队能得工程款2700元。
【点睛】
本题体现了数量关系式:工效之和×合作时间=工作总量;解答此题的关键是理解甲队完成了工作总量的几分之几,他应得的工程款也是总工程款的几分之几。
30.(1)40;70;30;(2)50%
【解析】
(1)良好的人数有60人,占总人数的30%,所以总人数有60÷30%=200(人)。用总人数分别乘20%、35%,求出优秀人数和达标人数,最后用总人数
解析:(1)40;70;30;(2)50%
【解析】
(1)良好的人数有60人,占总人数的30%,所以总人数有60÷30%=200(人)。用总人数分别乘20%、35%,求出优秀人数和达标人数,最后用总人数减去优秀人数、良好人数和达标人数,求出未达标的人数,从而填表。
(2)用良好的人数减去优秀的人数,再将差除以优秀的人数,求出良好的人数比优秀的人数多百分之几。
(1)总人数:60÷30%=200(人)
优秀人数:200×20%=40(人)
达标人数:200×35%=70(人)
未达标人数:200-40-60-70=30(人)
填表如下:
项目 优秀 良好 达标 未达标
人数 40 60 70 30
(2)(60-40)÷40×100%
=20÷40×100%
=50%
答:良好的人数比优秀的人数多50%。
【点睛】
本题考查了扇形统计图的应用,能根据扇形统计图获取有用信息是解题的关键。
31.80吨
【解析】
把原来每吨原材料的价格看作单位“1”,现在每吨原材料的价格=原来每吨原材料的价格×(1+25%),根据“总价=单价×数量”求出原来进100吨原材料需要的钱数,现在可以进的吨数=原来
解析:80吨
【解析】
把原来每吨原材料的价格看作单位“1”,现在每吨原材料的价格=原来每吨原材料的价格×(1+25%),根据“总价=单价×数量”求出原来进100吨原材料需要的钱数,现在可以进的吨数=原来进100吨原材料需要的钱数÷现在每吨原材料的价格,据此解答。
100×200÷[200×(1+25%)]
=100×200÷[200×1.25]
=100×200÷250
=20000÷250
=80(吨)
答:现在只能进80吨。
【点睛】
掌握单价、总价、数量之间的关系是解答题目的关键。
32.解:第一个图形中三角形个数:1个;
第二个图形中三角形个数:1×4+1=5(个);
第三个图形中三角形个数:2×4+1=9(个);
第四个图形中三角形个数:3×4+1=13(个);
第n个图形中三角
解析:解:第一个图形中三角形个数:1个;
第二个图形中三角形个数:1×4+1=5(个);
第三个图形中三角形个数:2×4+1=9(个);
第四个图形中三角形个数:3×4+1=13(个);
第n个图形中三角形个数:
(n-1)×4+1=(4n-3)(个)
4n-3=8057,n=2015.
答:n是第2015个图形.
【解析】
由已知图形中三角形个数推出三角形个数与图形个数之间的数量关系式,再根据题意代入数据计算即可解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
