15.3 分式方程课件(共59张PPT)
文档属性
| 名称 | 15.3 分式方程课件(共59张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 19:59:11 | ||
图片预览










文档简介
(共59张PPT)
(第二课时)
分式方程的应用
复习回顾
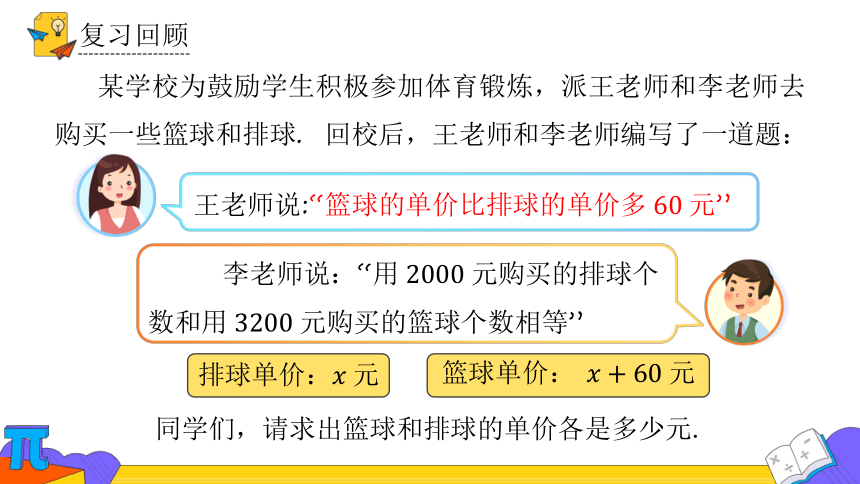
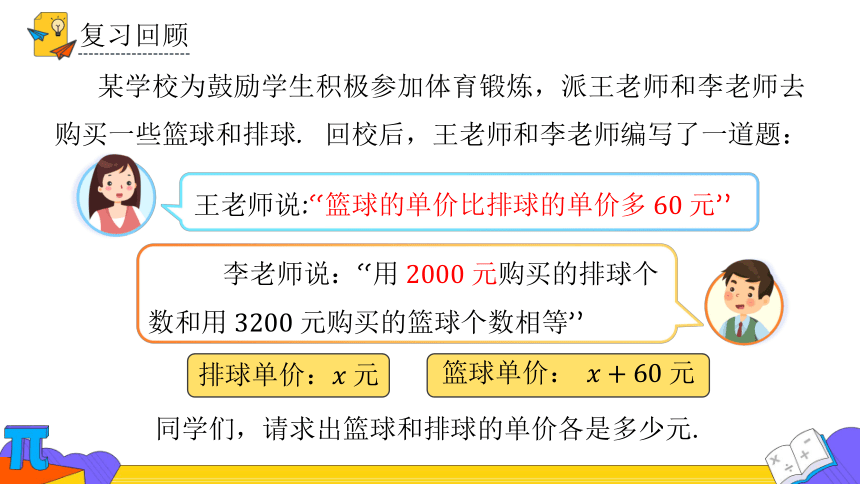
某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球. 回校后,王老师和李老师编写了一道题:
同学们,请求出篮球和排球的单价各是多少元.
30
王老师说:“篮球的单价比排球的单价多元”
总价单价数量
李老师说:“用元购买的排球个数和用元购买的篮球个数相等”
复习回顾
李老师说:“用元购买的排球个数和用元购买的篮球个数相等”
30
王老师说:“篮球的单价比排球的单价多元”
某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球. 回校后,王老师和李老师编写了一道题:
排球单价:元
篮球单价: 元
同学们,请求出篮球和排球的单价各是多少元.
复习回顾
李老师说:“用元购买的排球个数和用元购买的篮球个数相等”
30
王老师说:“篮球的单价比排球的单价多元”
某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球. 回校后,王老师和李老师编写了一道题:
同学们,请求出篮球和排球的单价各是多少元.
排球单价:元
篮球单价: 元
复习回顾
某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球. 回校后,王老师和李老师编写了一道题:
同学们,请求出篮球和排球的单价各是多少元.
李老师说:“用元购买的排球个数和用元购买的篮球个数相等”
30
王老师说:“篮球的单价比排球的单价多元”
排球单价:元
篮球单价: 元
复习回顾
排球个数:元
篮球个数:元
某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球. 回校后,王老师和李老师编写了一道题:
同学们,请求出篮球和排球的单价各是多少元.
李老师说:“用元购买的排球个数和用元购买的篮球个数相等”
30
王老师说:“篮球的单价比排球的单价多元”
设排球单价为元.
两边同乘,得 .
解得 .
检验:当 时,.
是方程的解,符合实际.
排球单价为元,篮球单价为元.
解:
答:
.
审:分析题意,找出数量关系和相等关系.
设:选择恰当的未知数,注意单位和语言完整.
1
2
5
验:双检验. 是否是所列方程的解;是否符合实际意义.
分式方程解决实际问题的一般步骤:
6
答:注意单位和语言完整.
列:根据数量和相等关系,正确列出代数式和方程.
3
解:认真仔细.
4
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
路程速度时间.
分析
行程问题
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
设提速前小轿车的速度为 .
分析
路程 速度 时间
提速前
提速后
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
设提速前小轿车的速度为 .
分析
路程 速度 时间
提速前
提速后
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
设提速前小轿车的速度为 .
分析
路程 速度 时间
提速前
提速后
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
设提速前小轿车的速度为 .
分析
路程 速度 时间
提速前
提速后
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
设提速前小轿车的速度为 .
分析
路程 速度 时间
提速前
提速后
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
设提速前小轿车的速度为 .
分析
路程 速度 时间
提速前
提速后
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
设提速前小轿车的速度为 .
分析
路程 速度 时间
提速前
提速后
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
设提速前小轿车的速度为 .
分析
路程 速度 时间
提速前
提速后
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
路程 速度 时间
提速前
提速后
设提速前小轿车的速度为 .
分析
相同的时间
路程 速度 时间
提速前
提速后
等量关系:提速前时间提时间
.
设提速前小轿车的速度为 .
两边同乘,得 .
解得
检验:由,都是正数,得 时,,
所以,原分式方程的解为
提速前小轿车的速度为.
.
解:
答:
.
.
审:分析题意,找出数量关系和相等关系.
设:选择恰当的未知数,注意单位和语言完整.
1
2
5
验:双检验.是否是所列方程的解;是否符合实际意义.
6
答:注意单位和语言完整.
列:根据数量和相等关系,正确列出代数式和方程.
3
解:认真仔细.
4
列分式方程解应用题的一般步骤:
,
分析
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
设船在静水中的速度为.
分析
路程 速度 时间
顺水
逆水
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
设船在静水中的速度为.
分析
路程 速度 时间
顺水
逆水
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
设船在静水中的速度为.
分析
路程 速度 时间
顺水
逆水
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
设船在静水中的速度为.
分析
路程 速度 时间
顺水
逆水
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
设船在静水中的速度为.
分析
路程 速度 时间
顺水
逆水
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
设船在静水中的速度为.
分析
路程 速度 时间
顺水
逆水
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
设船在静水中的速度为.
分析
路程 速度 时间
顺水
逆水
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
设船在静水中的速度为.
分析
路程 速度 时间
顺水
逆水
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
设船在静水中的速度为.
分析
路程 速度 时间
顺水
逆水
多用了
等量关系:顺水时间 逆水时间
.
路程 速度 时间
顺水
逆水
设船在静水中的速度为.
解得 .
检验:当 时,.
是方程的解,符合实际.
检验:当时,不符合实际.
船在静水中的速度为
解:
答:
.
路程速度时间.
分析
练习
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
路程 速度 时间
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
路程 速度 时间
设小轿车的速度为.
分析
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
路程 速度 时间
设小轿车的速度为.
分析
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
路程 速度 时间
设小轿车的速度为.
分析
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
路程 速度 时间
设小轿车的速度为.
分析
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
路程 速度 时间
设小轿车的速度为.
分析
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
路程 速度 时间
设小轿车的速度为.
分析
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
路程 速度 时间
设小轿车的速度为.
分析
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
路程 速度 时间
设小轿车的速度为.
分析
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
同时出发
等量关系:面包车行驶时间小轿车行驶的时间
.
路程 速度 时间
设小轿车的速度为.
两边同乘,得 .
解得 .
检验:当 时,.
是方程的解,符合实际.
面包车的速度为.
解:
答:
.
一轮船往返于两地之间,顺水比逆水快到达. 已知两地相距,水流速度是,求轮船在静水中的速度.
,
分析
练习
路程 速度 时间
顺水
逆水
设轮船在静水中的速度为.
分析
一轮船往返于两地之间,顺水比逆水快到达. 已知两地相距,水流速度是,求轮船在静水中的速度.
路程 速度 时间
顺水
逆水
设轮船在静水中的速度为.
分析
一轮船往返于两地之间,顺水比逆水快到达. 已知两地相距,水流速度是,求轮船在静水中的速度.
路程 速度 时间
顺水
逆水
设轮船在静水中的速度为.
分析
一轮船往返于两地之间,顺水比逆水快到达. 已知两地相距,水流速度是,求轮船在静水中的速度.
路程 速度 时间
顺水
逆水
设轮船在静水中的速度为.
分析
一轮船往返于两地之间,顺水比逆水快到达. 已知两地相距,水流速度是,求轮船在静水中的速度.
路程 速度 时间
顺水
逆水
设轮船在静水中的速度为.
分析
一轮船往返于两地之间,顺水比逆水快到达. 已知两地相距,水流速度是,求轮船在静水中的速度.
路程 速度 时间
顺水
逆水
设轮船在静水中的速度为.
分析
一轮船往返于两地之间,顺水比逆水快到达. 已知两地相距,水流速度是,求轮船在静水中的速度.
路程 速度 时间
顺水
逆水
设轮船在静水中的速度为.
分析
一轮船往返于两地之间,顺水比逆水快到达. 已知两地相距,水流速度是,求轮船在静水中的速度.
顺水比逆水快到达
等量关系:顺水时间 逆水时间
.
路程 速度 时间
顺水
逆水
设轮船在静水中的速度为.
两边同乘,得
.
解得 .
检验:当 时,.
是方程的解,符合实际.
检验:当时,不符合实际.
轮船在静水中的速度为
解:
答:
.
课
堂
小
结
列分式方程解应用题的步骤
实际问题
数学模型
审
本质
抽象
设
列
符号化
解
验
工具
答
条件限制
解决
农机厂到距工厂千米的向阳村检修农机,一部分人骑自行车先走,过了分钟,其余人乘汽车去,结果他们同时到达,已知汽车的速度是自行车的倍,求汽车的速度.
课后作业
1
列方程解决实际问题:
课后作业
2
列方程解决实际问题:
甲、乙两人分别从距离目的地和的两地同时出发,甲、乙的速度比是:,结果甲比乙提前到达目的地,求甲、乙的速度.
再 见
(第二课时)
分式方程的应用
复习回顾
某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球. 回校后,王老师和李老师编写了一道题:
同学们,请求出篮球和排球的单价各是多少元.
30
王老师说:“篮球的单价比排球的单价多元”
总价单价数量
李老师说:“用元购买的排球个数和用元购买的篮球个数相等”
复习回顾
李老师说:“用元购买的排球个数和用元购买的篮球个数相等”
30
王老师说:“篮球的单价比排球的单价多元”
某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球. 回校后,王老师和李老师编写了一道题:
排球单价:元
篮球单价: 元
同学们,请求出篮球和排球的单价各是多少元.
复习回顾
李老师说:“用元购买的排球个数和用元购买的篮球个数相等”
30
王老师说:“篮球的单价比排球的单价多元”
某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球. 回校后,王老师和李老师编写了一道题:
同学们,请求出篮球和排球的单价各是多少元.
排球单价:元
篮球单价: 元
复习回顾
某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球. 回校后,王老师和李老师编写了一道题:
同学们,请求出篮球和排球的单价各是多少元.
李老师说:“用元购买的排球个数和用元购买的篮球个数相等”
30
王老师说:“篮球的单价比排球的单价多元”
排球单价:元
篮球单价: 元
复习回顾
排球个数:元
篮球个数:元
某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球. 回校后,王老师和李老师编写了一道题:
同学们,请求出篮球和排球的单价各是多少元.
李老师说:“用元购买的排球个数和用元购买的篮球个数相等”
30
王老师说:“篮球的单价比排球的单价多元”
设排球单价为元.
两边同乘,得 .
解得 .
检验:当 时,.
是方程的解,符合实际.
排球单价为元,篮球单价为元.
解:
答:
.
审:分析题意,找出数量关系和相等关系.
设:选择恰当的未知数,注意单位和语言完整.
1
2
5
验:双检验. 是否是所列方程的解;是否符合实际意义.
分式方程解决实际问题的一般步骤:
6
答:注意单位和语言完整.
列:根据数量和相等关系,正确列出代数式和方程.
3
解:认真仔细.
4
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
路程速度时间.
分析
行程问题
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
设提速前小轿车的速度为 .
分析
路程 速度 时间
提速前
提速后
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
设提速前小轿车的速度为 .
分析
路程 速度 时间
提速前
提速后
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
设提速前小轿车的速度为 .
分析
路程 速度 时间
提速前
提速后
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
设提速前小轿车的速度为 .
分析
路程 速度 时间
提速前
提速后
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
设提速前小轿车的速度为 .
分析
路程 速度 时间
提速前
提速后
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
设提速前小轿车的速度为 .
分析
路程 速度 时间
提速前
提速后
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
设提速前小轿车的速度为 .
分析
路程 速度 时间
提速前
提速后
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
设提速前小轿车的速度为 .
分析
路程 速度 时间
提速前
提速后
例
小轿车平均提速,用相同的时间,小轿车提速前行驶,提速后比提速前多行驶,提速前小轿车的平均速度为多少?
路程 速度 时间
提速前
提速后
设提速前小轿车的速度为 .
分析
相同的时间
路程 速度 时间
提速前
提速后
等量关系:提速前时间提时间
.
设提速前小轿车的速度为 .
两边同乘,得 .
解得
检验:由,都是正数,得 时,,
所以,原分式方程的解为
提速前小轿车的速度为.
.
解:
答:
.
.
审:分析题意,找出数量关系和相等关系.
设:选择恰当的未知数,注意单位和语言完整.
1
2
5
验:双检验.是否是所列方程的解;是否符合实际意义.
6
答:注意单位和语言完整.
列:根据数量和相等关系,正确列出代数式和方程.
3
解:认真仔细.
4
列分式方程解应用题的一般步骤:
,
分析
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
设船在静水中的速度为.
分析
路程 速度 时间
顺水
逆水
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
设船在静水中的速度为.
分析
路程 速度 时间
顺水
逆水
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
设船在静水中的速度为.
分析
路程 速度 时间
顺水
逆水
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
设船在静水中的速度为.
分析
路程 速度 时间
顺水
逆水
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
设船在静水中的速度为.
分析
路程 速度 时间
顺水
逆水
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
设船在静水中的速度为.
分析
路程 速度 时间
顺水
逆水
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
设船在静水中的速度为.
分析
路程 速度 时间
顺水
逆水
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
设船在静水中的速度为.
分析
路程 速度 时间
顺水
逆水
例
一艘轮船逆流航行的时间比顺流航行的时间多用了,已知水速为,求船在静水中的速度.
设船在静水中的速度为.
分析
路程 速度 时间
顺水
逆水
多用了
等量关系:顺水时间 逆水时间
.
路程 速度 时间
顺水
逆水
设船在静水中的速度为.
解得 .
检验:当 时,.
是方程的解,符合实际.
检验:当时,不符合实际.
船在静水中的速度为
解:
答:
.
路程速度时间.
分析
练习
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
路程 速度 时间
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
路程 速度 时间
设小轿车的速度为.
分析
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
路程 速度 时间
设小轿车的速度为.
分析
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
路程 速度 时间
设小轿车的速度为.
分析
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
路程 速度 时间
设小轿车的速度为.
分析
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
路程 速度 时间
设小轿车的速度为.
分析
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
路程 速度 时间
设小轿车的速度为.
分析
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
路程 速度 时间
设小轿车的速度为.
分析
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
路程 速度 时间
设小轿车的速度为.
分析
朋友们约好一起开着辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后. 他们同时出发,当面包车行驶了时,发现小轿车只行驶了若面包车的行驶速度比小轿车快,请问面包车的速度为多少?
同时出发
等量关系:面包车行驶时间小轿车行驶的时间
.
路程 速度 时间
设小轿车的速度为.
两边同乘,得 .
解得 .
检验:当 时,.
是方程的解,符合实际.
面包车的速度为.
解:
答:
.
一轮船往返于两地之间,顺水比逆水快到达. 已知两地相距,水流速度是,求轮船在静水中的速度.
,
分析
练习
路程 速度 时间
顺水
逆水
设轮船在静水中的速度为.
分析
一轮船往返于两地之间,顺水比逆水快到达. 已知两地相距,水流速度是,求轮船在静水中的速度.
路程 速度 时间
顺水
逆水
设轮船在静水中的速度为.
分析
一轮船往返于两地之间,顺水比逆水快到达. 已知两地相距,水流速度是,求轮船在静水中的速度.
路程 速度 时间
顺水
逆水
设轮船在静水中的速度为.
分析
一轮船往返于两地之间,顺水比逆水快到达. 已知两地相距,水流速度是,求轮船在静水中的速度.
路程 速度 时间
顺水
逆水
设轮船在静水中的速度为.
分析
一轮船往返于两地之间,顺水比逆水快到达. 已知两地相距,水流速度是,求轮船在静水中的速度.
路程 速度 时间
顺水
逆水
设轮船在静水中的速度为.
分析
一轮船往返于两地之间,顺水比逆水快到达. 已知两地相距,水流速度是,求轮船在静水中的速度.
路程 速度 时间
顺水
逆水
设轮船在静水中的速度为.
分析
一轮船往返于两地之间,顺水比逆水快到达. 已知两地相距,水流速度是,求轮船在静水中的速度.
路程 速度 时间
顺水
逆水
设轮船在静水中的速度为.
分析
一轮船往返于两地之间,顺水比逆水快到达. 已知两地相距,水流速度是,求轮船在静水中的速度.
顺水比逆水快到达
等量关系:顺水时间 逆水时间
.
路程 速度 时间
顺水
逆水
设轮船在静水中的速度为.
两边同乘,得
.
解得 .
检验:当 时,.
是方程的解,符合实际.
检验:当时,不符合实际.
轮船在静水中的速度为
解:
答:
.
课
堂
小
结
列分式方程解应用题的步骤
实际问题
数学模型
审
本质
抽象
设
列
符号化
解
验
工具
答
条件限制
解决
农机厂到距工厂千米的向阳村检修农机,一部分人骑自行车先走,过了分钟,其余人乘汽车去,结果他们同时到达,已知汽车的速度是自行车的倍,求汽车的速度.
课后作业
1
列方程解决实际问题:
课后作业
2
列方程解决实际问题:
甲、乙两人分别从距离目的地和的两地同时出发,甲、乙的速度比是:,结果甲比乙提前到达目的地,求甲、乙的速度.
再 见
