第四单元《图形的相似》质量检测试卷B(含答案)
文档属性
| 名称 | 第四单元《图形的相似》质量检测试卷B(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-28 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
北师大版2022-2023学年九年级(上)第四章图形的相似检测试卷B
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 如果两个相似三角形的周长比为 ,那么它们的对应角平分线的比为
A. B. C. D.
2. 在比例尺为 的地图上,如果A,B两地的距离是 厘米,那么这两地的实际距离是
A. 米 B. 米 C. 米 D. 米
3. 如果点 是线段 的黄金分割点,且 ,即,那么 的值等于
A. B. C. D.
4. 下列命题中,说法正确的是
A. 所有菱形都相似
B. 两边对应成比例且有一组角对应相等的两个三角形相似
C. 三角形的重心到一个顶点的距离,等于它到这个顶点对边距离的两倍
D. 斜边和直角边对应成比例,两个直角三角形相似
5. 如图, 是平行四边形 的对角线 上一点, 的延长线交 于点 ,交 的延长线于点 ,图中相似三角形有
A. 对 B. 对 C. 对 D. 对
6. 已知在 中,,,,如果 与 相似,且 两条边的长分别为 和 ,那么 第三条边的长为
A. B. C. D.
7. 下列图形,一定相似的是
A. 两个直角三角形 B. 两个等腰三角形
C. 两个等边三角形 D. 两个菱形
8. 在 中,点 ,, 分别在边 ,, 上,连接 ,,如果 ,,,那么 的值是
A. B. C. D.
9. 如图,在剧场中,坐在小明()前面一排的女士()戴着高帽子(),此时小明的眼睛 ,帽顶 以及舞台上方横梁的某点 在同一条直线上;女士发现帽子挡住了小明的视线,于是摘掉帽子,此时小明的眼睛 ,女士头顶 以及舞台下方地面上某点 在同一条直线上.已知舞台的高 ,,, 在同一条直线上,,, 在同一条直线上,,,则舞台横梁到舞台的距离 为
A. B. C. D.
10. 下列说法中,正确的个数是
①位似图形一定是相似图形;②相似图形一定是位似图形;③位似中心要么取在图形外部,要么取在图形内部;④若五边形 与五边形 位似,则其中 与 也是位似的,且相似比相等.
A. 个 B. 个 C. 个 D. 个
11. 制作一块 长方形广告牌的成本是 元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的 倍,则扩大后长方形广告牌的成本是
A. 元 B. 元 C. 元 D. 元
12. 如图,,,,,,,,, 都是方格纸的格点,为使 ,则点 应是 ,,, 点中的
A. B. C. D.
二、填空题(共6小题;每小题4分,共24分)
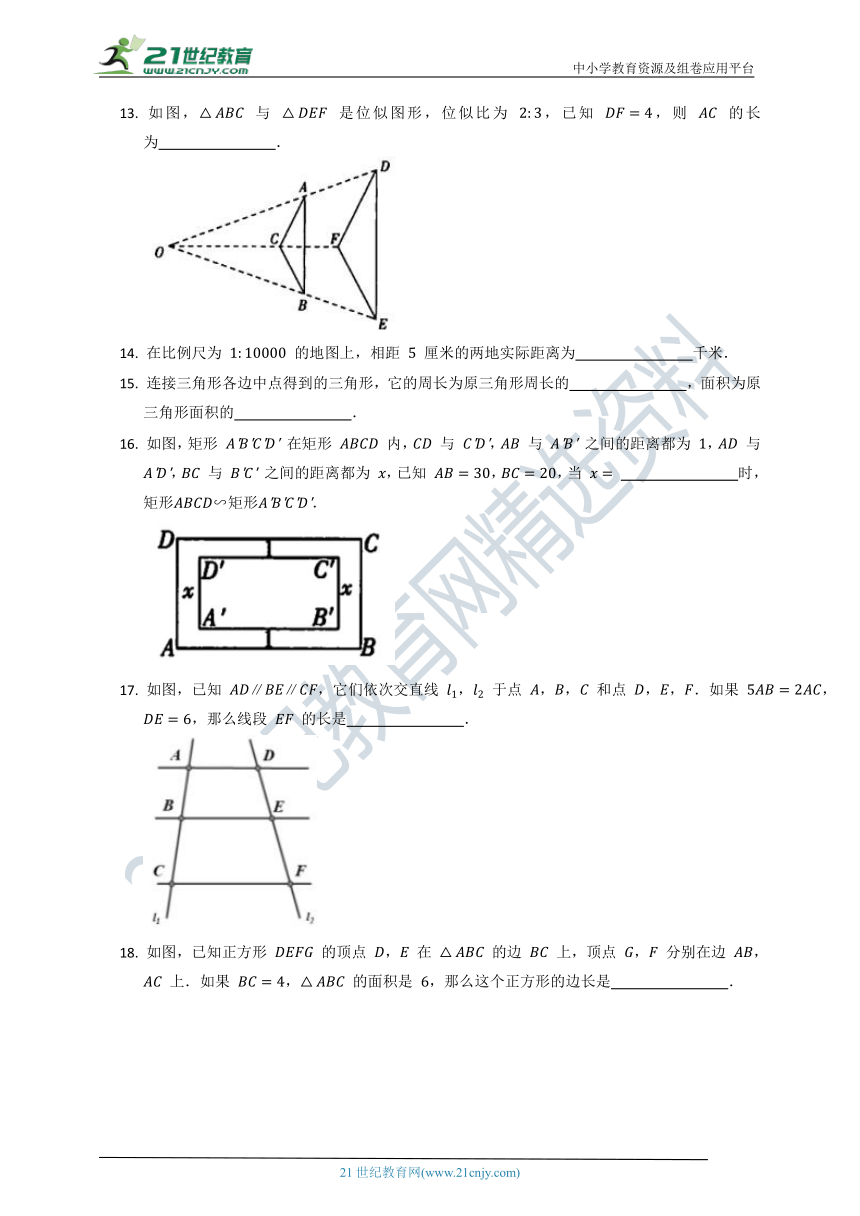
13. 如图, 与 是位似图形,位似比为 ,已知 ,则 的长为 .
14. 在比例尺为 的地图上,相距 厘米的两地实际距离为 千米.
15. 连接三角形各边中点得到的三角形,它的周长为原三角形周长的 ,面积为原三角形面积的 .
16. 如图,矩形 在矩形 内, 与 , 与 之间的距离都为 , 与 , 与 之间的距离都为 ,已知 ,,当 时,.
17. 如图,已知 ,它们依次交直线 , 于点 ,, 和点 ,,.如果 ,,那么线段 的长是 .
18. 如图,已知正方形 的顶点 , 在 的边 上,顶点 , 分别在边 , 上.如果 , 的面积是 ,那么这个正方形的边长是 .
三、解答题(共7小题;共60分)
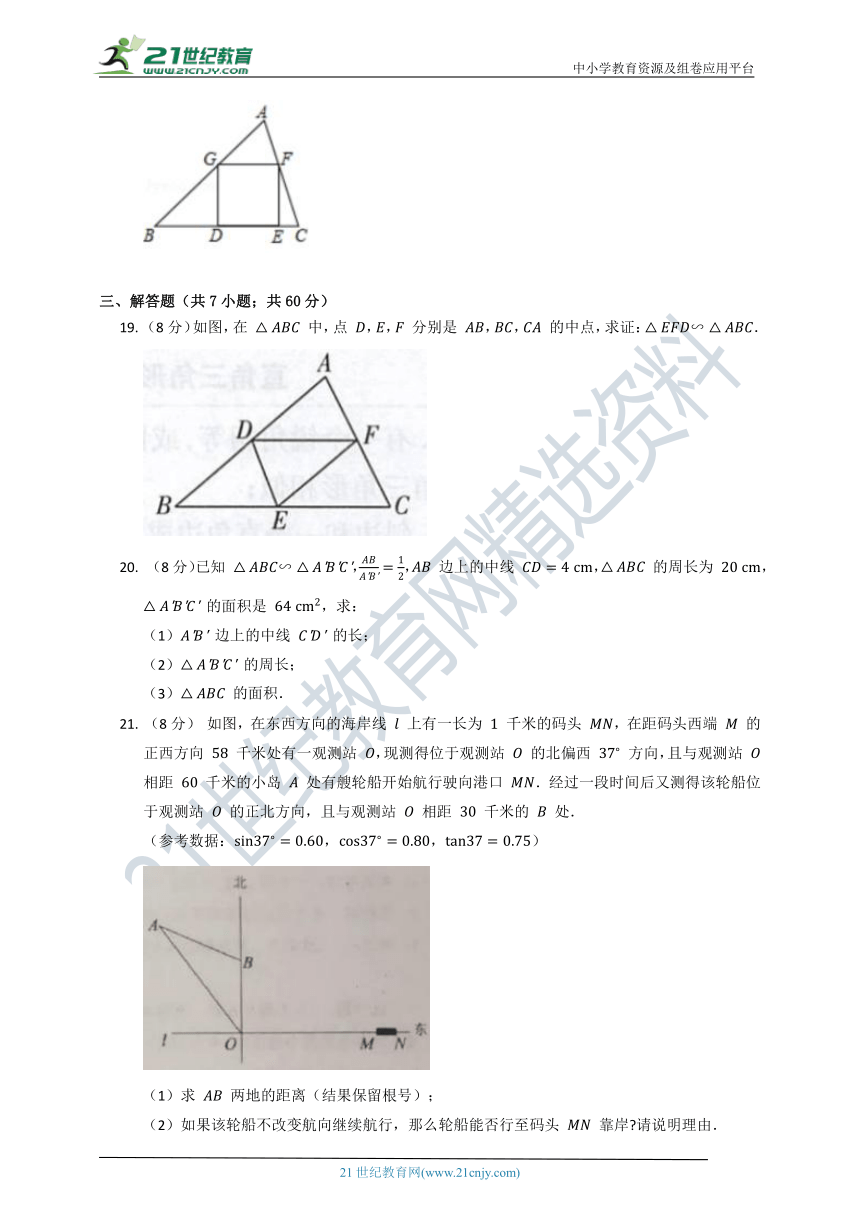
19. (8分)如图,在 中,点 ,, 分别是 ,, 的中点,求证:.
20. (8分)已知 ,, 边上的中线 , 的周长为 , 的面积是 ,求:
(1) 边上的中线 的长;
(2) 的周长;
(3) 的面积.
21. (8分) 如图,在东西方向的海岸线 上有一长为 千米的码头 ,在距码头西端 的正西方向 千米处有一观测站 ,现测得位于观测站 的北偏西 方向,且与观测站 相距 千米的小岛 处有艘轮船开始航行驶向港口 .经过一段时间后又测得该轮船位于观测站 的正北方向,且与观测站 相距 千米的 处.
(参考数据:,,)
(1)求 两地的距离(结果保留根号);
(2)如果该轮船不改变航向继续航行,那么轮船能否行至码头 靠岸 请说明理由.
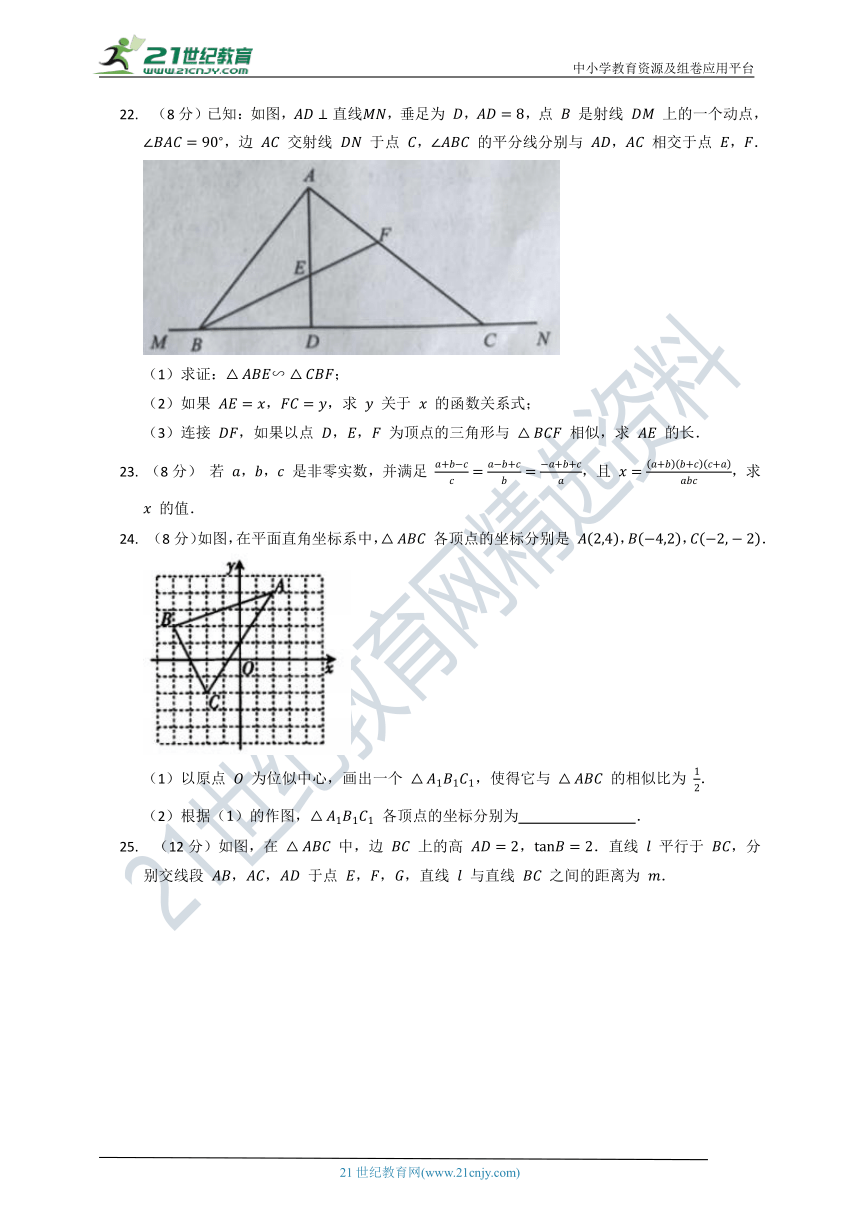
22. (8分)已知:如图,,垂足为 ,,点 是射线 上的一个动点,,边 交射线 于点 , 的平分线分别与 , 相交于点 ,.
(1)求证:;
(2)如果 ,,求 关于 的函数关系式;
(3)连接 ,如果以点 ,, 为顶点的三角形与 相似,求 的长.
23. (8分) 若 ,, 是非零实数,并满足 ,且 ,求 的值.
24. (8分)如图,在平面直角坐标系中, 各顶点的坐标分别是 ,,.
(1)以原点 为位似中心,画出一个 ,使得它与 的相似比为 .
(2)根据()的作图, 各顶点的坐标分别为 .
25. (12分)如图,在 中,边 上的高 ,.直线 平行于 ,分别交线段 ,, 于点 ,,,直线 与直线 之间的距离为 .
(1)当 时,求 的值;
(2)将 沿着 翻折,点 落在两平行直线 与 之间的点 处,延长 交线段 于点 .
①当点 恰好为 的重心时,求此时 的长.
②连接 ,在 的条件下,如果 与 相似,试用 的代数式表示线段 的长.
答案
第一部分
1. A
【解析】 两个相似三角形的周长比为 ,
两个相似三角形的相似比为 ,
它们的对应角平分线之比为 .
2. C
【解析】根据题意, 厘米 米.
即两地间的实际距离是 米.
故选C.
3. D
【解析】由于 为线段 的黄金分割点,
且 ,
则 .
4. D
【解析】A.所有菱形不一定相似,故该选项不正确,不符合题意;
B.两边对应成比例且夹角对应相等的两个三角形相似,故该选项不正确,不符合题意;
C.三角形的重心到一个顶点的距离,等于它到这个顶点对边中点距离的两倍,故该选项不正确,不符合题意;
D.斜边和直角边对应成比例,两个直角三角形相似,故该选项正确,符合题意.
5. A
【解析】 四边形 是平行四边形,
,,,
,
,,
,
,,
,
则图中相似三角形有 对,它们分别是:,,,,,,
故选:A.
6. C
7. C
【解析】A.两个直角三角形,不一定有锐角相等,故不一定相似;
B.两个等腰三角形顶角不一定相等,故不一定相似;
C.两个等边三角形,角都是 ,故相似;
D.任意两个菱形的对应边的比相等,但对应角不一定相等,故不一定相似.
8. B
【解析】如图:
,
,
,
,
.
9. D
【解析】由题意知,,, 都垂直于地面 ,
,
,
.
,
,
.
,,,,
,
,
.
10. B
11. C
【解析】将此广告牌的四边都扩大为原来的 倍,则面积扩大为原来的 倍,
扩大后长方形广告牌的面积 ,
长方形广告牌每平方米的制作成本是 元,
扩大后长方形广告牌的成本是 元.
12. B
第二部分
13.
【解析】因为 与 是位似图形,位似比为 ,
所以 ,
所以 ,
则 .
14.
15. ,
16.
17.
【解析】,
,
,
设 ,则 ,
,
,
,
解得:,经检验符合题意;
故答案为:.
18.
【解析】作 于 ,交 于 ,如图,
的面积是 ,
,
,
设正方形 的边长为 ,则 ,,,
,
,
,即 ,解得 ,
即正方形 的边长为 .
故答案为 .
第三部分
19. 点 ,, 分别是 ,, 的中点,
,, 是 的中位线.
,,.
.
.
20. (1) ,,
,
又 ,
.
(2) ,,
,
又 的周长为 ,
.
(3) ,,
,
又 的面积是 ,
.
21. (1) 过点 作 于点 .
由题意,得 ,,,,
,,
,
.
(2) 如果该轮船不改变航向继续航行,那么轮船不能行至码头 靠岸.
延长 交 于 ,
,
,
,
,解得 ,
,,
,
,
如果该轮船不改变航向继续航行,那么轮船不能行至码头 靠岸.
22. (1) ,,
,,
,
平分 ,
,
.
(2) 作 垂足为点 ,
,
,
,,
,
;
平分 ,,,
,
,,
,
,
,即 ,
解得:.
(3) 如图,连接 ,
设 ,由 ,如果以点 ,, 为顶点的三角形与 相似,即以点 ,, 为顶点的三角形与 相似,
,
若 ,则 ,
,
,
,
,
,
,
,
又 ,
,
,
由()得:,
,
解得:(舍去负值),
,
若 ,则 ,
,即 ,
,
,
,
由()得: ,
是锐角,而 是直角,所以这种情况不成立.
综上所述,如果以点 ,, 为顶点的三角形与 相似, 的长为 .
23. 或 .
24. (1) 如图, 即为所求.
(2) ,,
25. (1) 由 是边 上的高,,,得 .
由题意得 ,.
直线 平行 ,
.
根据题意,得 是 的高,
.
得 ,解得 .
即 的值为 .
(2) ①由 沿着 翻折,点 落在两平行直线 与 之间的点 处,得点 落在 上.
点 为 的重心,
为 的中线,.
可得 ,.
由 沿着 翻折,可得 .
直线 平行 ,可得 ,.
,得 .
.得 ,解得 .
② ,,
与 相似有两种可能性.
由 与 相似,得 与 相似.
由 ,得 ,,,,.
i.当 时,由 ,得 .化简得 .
ii.当 时,作 边 上的高 ,得 .
由 ,得 .化简得 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版2022-2023学年九年级(上)第四章图形的相似检测试卷B
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 如果两个相似三角形的周长比为 ,那么它们的对应角平分线的比为
A. B. C. D.
2. 在比例尺为 的地图上,如果A,B两地的距离是 厘米,那么这两地的实际距离是
A. 米 B. 米 C. 米 D. 米
3. 如果点 是线段 的黄金分割点,且 ,即,那么 的值等于
A. B. C. D.
4. 下列命题中,说法正确的是
A. 所有菱形都相似
B. 两边对应成比例且有一组角对应相等的两个三角形相似
C. 三角形的重心到一个顶点的距离,等于它到这个顶点对边距离的两倍
D. 斜边和直角边对应成比例,两个直角三角形相似
5. 如图, 是平行四边形 的对角线 上一点, 的延长线交 于点 ,交 的延长线于点 ,图中相似三角形有
A. 对 B. 对 C. 对 D. 对
6. 已知在 中,,,,如果 与 相似,且 两条边的长分别为 和 ,那么 第三条边的长为
A. B. C. D.
7. 下列图形,一定相似的是
A. 两个直角三角形 B. 两个等腰三角形
C. 两个等边三角形 D. 两个菱形
8. 在 中,点 ,, 分别在边 ,, 上,连接 ,,如果 ,,,那么 的值是
A. B. C. D.
9. 如图,在剧场中,坐在小明()前面一排的女士()戴着高帽子(),此时小明的眼睛 ,帽顶 以及舞台上方横梁的某点 在同一条直线上;女士发现帽子挡住了小明的视线,于是摘掉帽子,此时小明的眼睛 ,女士头顶 以及舞台下方地面上某点 在同一条直线上.已知舞台的高 ,,, 在同一条直线上,,, 在同一条直线上,,,则舞台横梁到舞台的距离 为
A. B. C. D.
10. 下列说法中,正确的个数是
①位似图形一定是相似图形;②相似图形一定是位似图形;③位似中心要么取在图形外部,要么取在图形内部;④若五边形 与五边形 位似,则其中 与 也是位似的,且相似比相等.
A. 个 B. 个 C. 个 D. 个
11. 制作一块 长方形广告牌的成本是 元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的 倍,则扩大后长方形广告牌的成本是
A. 元 B. 元 C. 元 D. 元
12. 如图,,,,,,,,, 都是方格纸的格点,为使 ,则点 应是 ,,, 点中的
A. B. C. D.
二、填空题(共6小题;每小题4分,共24分)
13. 如图, 与 是位似图形,位似比为 ,已知 ,则 的长为 .
14. 在比例尺为 的地图上,相距 厘米的两地实际距离为 千米.
15. 连接三角形各边中点得到的三角形,它的周长为原三角形周长的 ,面积为原三角形面积的 .
16. 如图,矩形 在矩形 内, 与 , 与 之间的距离都为 , 与 , 与 之间的距离都为 ,已知 ,,当 时,.
17. 如图,已知 ,它们依次交直线 , 于点 ,, 和点 ,,.如果 ,,那么线段 的长是 .
18. 如图,已知正方形 的顶点 , 在 的边 上,顶点 , 分别在边 , 上.如果 , 的面积是 ,那么这个正方形的边长是 .
三、解答题(共7小题;共60分)
19. (8分)如图,在 中,点 ,, 分别是 ,, 的中点,求证:.
20. (8分)已知 ,, 边上的中线 , 的周长为 , 的面积是 ,求:
(1) 边上的中线 的长;
(2) 的周长;
(3) 的面积.
21. (8分) 如图,在东西方向的海岸线 上有一长为 千米的码头 ,在距码头西端 的正西方向 千米处有一观测站 ,现测得位于观测站 的北偏西 方向,且与观测站 相距 千米的小岛 处有艘轮船开始航行驶向港口 .经过一段时间后又测得该轮船位于观测站 的正北方向,且与观测站 相距 千米的 处.
(参考数据:,,)
(1)求 两地的距离(结果保留根号);
(2)如果该轮船不改变航向继续航行,那么轮船能否行至码头 靠岸 请说明理由.
22. (8分)已知:如图,,垂足为 ,,点 是射线 上的一个动点,,边 交射线 于点 , 的平分线分别与 , 相交于点 ,.
(1)求证:;
(2)如果 ,,求 关于 的函数关系式;
(3)连接 ,如果以点 ,, 为顶点的三角形与 相似,求 的长.
23. (8分) 若 ,, 是非零实数,并满足 ,且 ,求 的值.
24. (8分)如图,在平面直角坐标系中, 各顶点的坐标分别是 ,,.
(1)以原点 为位似中心,画出一个 ,使得它与 的相似比为 .
(2)根据()的作图, 各顶点的坐标分别为 .
25. (12分)如图,在 中,边 上的高 ,.直线 平行于 ,分别交线段 ,, 于点 ,,,直线 与直线 之间的距离为 .
(1)当 时,求 的值;
(2)将 沿着 翻折,点 落在两平行直线 与 之间的点 处,延长 交线段 于点 .
①当点 恰好为 的重心时,求此时 的长.
②连接 ,在 的条件下,如果 与 相似,试用 的代数式表示线段 的长.
答案
第一部分
1. A
【解析】 两个相似三角形的周长比为 ,
两个相似三角形的相似比为 ,
它们的对应角平分线之比为 .
2. C
【解析】根据题意, 厘米 米.
即两地间的实际距离是 米.
故选C.
3. D
【解析】由于 为线段 的黄金分割点,
且 ,
则 .
4. D
【解析】A.所有菱形不一定相似,故该选项不正确,不符合题意;
B.两边对应成比例且夹角对应相等的两个三角形相似,故该选项不正确,不符合题意;
C.三角形的重心到一个顶点的距离,等于它到这个顶点对边中点距离的两倍,故该选项不正确,不符合题意;
D.斜边和直角边对应成比例,两个直角三角形相似,故该选项正确,符合题意.
5. A
【解析】 四边形 是平行四边形,
,,,
,
,,
,
,,
,
则图中相似三角形有 对,它们分别是:,,,,,,
故选:A.
6. C
7. C
【解析】A.两个直角三角形,不一定有锐角相等,故不一定相似;
B.两个等腰三角形顶角不一定相等,故不一定相似;
C.两个等边三角形,角都是 ,故相似;
D.任意两个菱形的对应边的比相等,但对应角不一定相等,故不一定相似.
8. B
【解析】如图:
,
,
,
,
.
9. D
【解析】由题意知,,, 都垂直于地面 ,
,
,
.
,
,
.
,,,,
,
,
.
10. B
11. C
【解析】将此广告牌的四边都扩大为原来的 倍,则面积扩大为原来的 倍,
扩大后长方形广告牌的面积 ,
长方形广告牌每平方米的制作成本是 元,
扩大后长方形广告牌的成本是 元.
12. B
第二部分
13.
【解析】因为 与 是位似图形,位似比为 ,
所以 ,
所以 ,
则 .
14.
15. ,
16.
17.
【解析】,
,
,
设 ,则 ,
,
,
,
解得:,经检验符合题意;
故答案为:.
18.
【解析】作 于 ,交 于 ,如图,
的面积是 ,
,
,
设正方形 的边长为 ,则 ,,,
,
,
,即 ,解得 ,
即正方形 的边长为 .
故答案为 .
第三部分
19. 点 ,, 分别是 ,, 的中点,
,, 是 的中位线.
,,.
.
.
20. (1) ,,
,
又 ,
.
(2) ,,
,
又 的周长为 ,
.
(3) ,,
,
又 的面积是 ,
.
21. (1) 过点 作 于点 .
由题意,得 ,,,,
,,
,
.
(2) 如果该轮船不改变航向继续航行,那么轮船不能行至码头 靠岸.
延长 交 于 ,
,
,
,
,解得 ,
,,
,
,
如果该轮船不改变航向继续航行,那么轮船不能行至码头 靠岸.
22. (1) ,,
,,
,
平分 ,
,
.
(2) 作 垂足为点 ,
,
,
,,
,
;
平分 ,,,
,
,,
,
,
,即 ,
解得:.
(3) 如图,连接 ,
设 ,由 ,如果以点 ,, 为顶点的三角形与 相似,即以点 ,, 为顶点的三角形与 相似,
,
若 ,则 ,
,
,
,
,
,
,
,
又 ,
,
,
由()得:,
,
解得:(舍去负值),
,
若 ,则 ,
,即 ,
,
,
,
由()得: ,
是锐角,而 是直角,所以这种情况不成立.
综上所述,如果以点 ,, 为顶点的三角形与 相似, 的长为 .
23. 或 .
24. (1) 如图, 即为所求.
(2) ,,
25. (1) 由 是边 上的高,,,得 .
由题意得 ,.
直线 平行 ,
.
根据题意,得 是 的高,
.
得 ,解得 .
即 的值为 .
(2) ①由 沿着 翻折,点 落在两平行直线 与 之间的点 处,得点 落在 上.
点 为 的重心,
为 的中线,.
可得 ,.
由 沿着 翻折,可得 .
直线 平行 ,可得 ,.
,得 .
.得 ,解得 .
② ,,
与 相似有两种可能性.
由 与 相似,得 与 相似.
由 ,得 ,,,,.
i.当 时,由 ,得 .化简得 .
ii.当 时,作 边 上的高 ,得 .
由 ,得 .化简得 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
