人教版七年级上册第3章一元一次方程全章学案21页
文档属性
| 名称 | 人教版七年级上册第3章一元一次方程全章学案21页 |

|
|
| 格式 | zip | ||
| 文件大小 | 659.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-22 00:00:00 | ||
图片预览




文档简介
第三章 一元一次方程
3.1.1一元一次方程
学习目标
1.了解等式与方程的区别与联系.
2.掌握一元一次方程、方程的解及解方程的有关概念.
3.通过算术法和列方程的比较,体会从算式到方程的进步.
自主预习
1.一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70km/h,卡车的行驶速度是60km/h客车比卡车早1h经过B地.A,B两地间的路程是多少?
(1)用算术法解决这个问题;
(2)用方程表示该问题(只列方程不解).
2.根据下列问题,设未知数并列出方程:
(1)用一根长24cm的铁丝围成一个正方形,正方形的边长是多少?
(2)一台计算机已使用1700小时,预计每月再使用150小时,经过多少月这台计算机的使用时间达到规定的检修时间2450小时?
(3)某校女生占全体学生数的52%,比男生多80人,这个学校有多少学生?
3.观察下列式子:①7+3=10;②3x-5=1;③5x-2x;④2x-l≠x;⑤x-1=7;⑥=3.其中 是等式, 是方程; 是一元一次方程(填序号).
4.括号里的数(x=3,x=4,x=-4)是x(x+1)=12的解的有 .
课堂探究
探究一 等式与方程
1.___________________________________叫等式;_________________________________叫方程.
2.式子①②③④ ⑤⑥⑦中等式是________________________;
方程是___________________________.
归纳:
等式与方程的区别与联系:
探究二 一元一次方程
观察下列方程,你能说出它们的共同特征吗?
① ②
③④
归纳:
只含有_______个未知数,未知数的次数都是_______,等号两边都是_______,这样的方程叫做一元一次方程.
探究三 解方程与方程的解
1.解方程的定义:
2.方程的解的定义:
重点题型
题型一 一元一次方程的概念
1.下列各式中①② ③ ④是一元一次方程的是_______.
2.已知方程是一元一次方程,则n=_______.
3.是关于x 的一元一次方程,则k=_________
题型二 方程的解
4.已知是方程的解,则m=_________.
5.写出一个以为解的一元一次方程_______________________.
随堂训练
1.下列方程:①x-1=5;②-x=;③=5;④x(x+1)=2;⑤4-2x=x+1中是一元一次方程是( )
A.①② B.①②③
C.①②③⑤ D.①②⑤
2.已知(2m-3)x-(2-3m)x=1是关于x的一元一次方程,则m=_______.
3.请写出一个解为2的关于x的一元一次方程: .
4.已知x的2倍与2x-4的值互为相反数,则可列方程为 .
5.一个两位数,十位上数字为a,个位数字比a大2,且十位上数与个位上数和为6,列方程为________.
6.检验方程后面大括号内所列各数是否为前面方程的解: =2x-l,{2,-5}.
7.只列出方程:
(1)小明买了4个笔记本和3支圆珠笔一共用了4.7元,已知笔记本每本0.8元,圆珠笔每支多少元?
(2)甲、乙两个运输队,甲队32人,乙队28人,若从乙队调走若干人到甲队,那么甲队人数恰好是乙队人数的2倍,求从乙队调走多少人到甲队?
能力提升
1.已知是关于x的一元一次方程,求k的值.
2.七年级一班的一个综合实践活动小组去A、B两个超市调查去年和今年五一期间的销售情况,如图是调查后小敏与其他两位同学进行交流的情景,根据他们的对话,求A、B两个超市今年五一期问的销售额(只列方程).
3.在一次植树活动中,甲班植树的株数比乙班多20%,乙班植树的株树比甲班的一半多10株.设乙班植树x株.
(1)列两个不同的含x的代数式,分别表示甲班植树的株数;
(2)根据题意列出含未知数x的方程;
(3)检验乙班、甲班植树株数是不是分别为25株和35株.
数学广角
方程小史
“方程”一词来源于我国古算书《九章算术》.在这部著作中,已经会列一元一次方程.
宋元时期,中国数学家创立了“天元术”,用天元表示未知数进而建立方程.这种方法的代表作是数学家李冶写的《测圆海镜》书中所说的“立天元一”相当于现在的“设未知数x”.
清代数学家李善兰翻译外国数学著作时,开始将equation一词译为“方程”,至今一直这样沿用.
第三章 一元一次方程
3.1.2 等式的性质
学习目标
1.掌握等式的两条性质.
2.会用等式的性质解简单的一元一次方程.
3.初步具有解方程中的化归意识.
自主预习
1.如果a=b,那么ac= ;
如果a=b(c≠O),那么= .
2.说出下列各式变形的根据.
(1)由2a+5-a,
得2a-a+5.( )
(2)由-2x=8,
得x=-4.( )
(3)由3x=2+2x,
得x=2.( )
(4)由-x=2,
得x=-6.( )
3.利用等式的性质解方程:
(1)x+5=13;
(2)-x-3=5.
课堂探究
探究一 等式的性质
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡.
1.如图,由左边天平到右边天平或由右边天平到左边天平发生怎样的变化?你发现了什么事实?
归纳:
等式性质1: 等式两边加(或减)__________,结果_____________.
用字母表示为:如果________,那么______.
2.如图,由左边天平到右边天平或由右边天平到左边天平发生怎样的变化?你发现了什么事实?
归纳:
等式性质2: 等式两边同乘一个数或除__________结果______________.
用字母表示为:如果________,那么________ 如果________,那么________.
3.下列运用等式的性质对等式进行的变形中,正确的是( ).
A.由3+x=5,得x=5+3 B.由7x=-4,得x=-
C.由y=0,得y=2 D.由3=x-2,得-x=-2-3
探究二 利用等式的性质解方程
利用等式的性质解方程:
(1)x+7=26;
(2)-5x=20;
(3)- x-5=4.
重点题型
题型 等式性质的应用
1.用适当的数或字母填空,使所得结果仍是等式.
(1)如果x-5=-1,那么x= ;
(2)如果,那么a= ;
(3)如果-2x=8,那么x= ;
(4)如果2x-3=3x,那么x= .
2.已知m+a=n+b,根据等式性质变形为m=n,那么a,b必须满足的条件是 ( )
A.a=-b B.-a=b
C.a=b D.a,b可以是任意整式
3. 如果ma=mb,那么下列等式中,不一定成立的是( )
A.ma+1=mb+1 B.ma-3=mb-3
C.-2ma=-2mb D.a=b
随堂训练
1.用适当的数或字母填空,使所得结果仍是等式.
(1)如果那么 ;
(2)如果那么 .
2.下列各式变形正确的是( )
A.由
B.由
C.由
D.由
3.已知根据等式性质变形
那么必须满足的条件是( )
A. B.
C. D.可以是任意整式
4.由,得,其依据是 .
5.用等式的性质解释下列方程:
.
能力提升
1. 下列变形不正确的是 ( )
A.若2R=2r (0),得R=r
B.若a=b,则
C.若,则
D.若,得
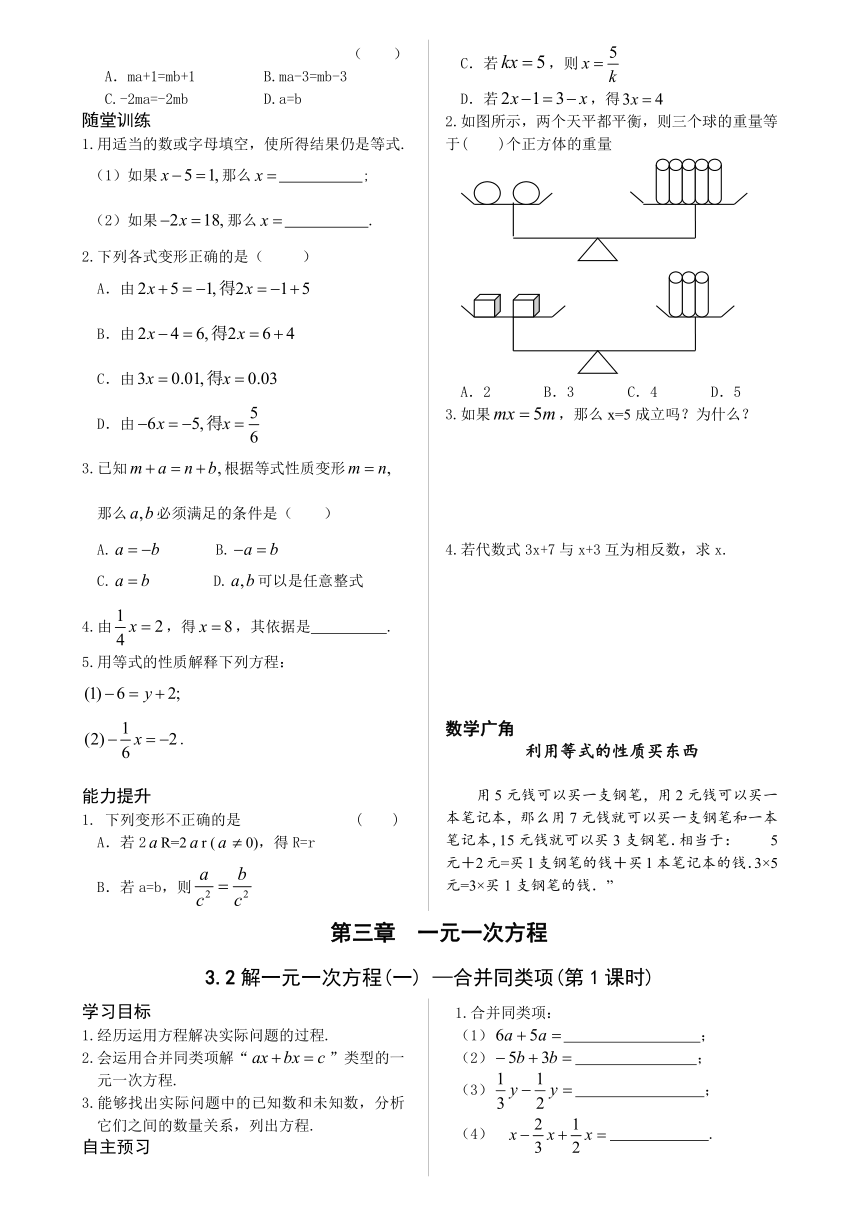
2.如图所示,两个天平都平衡,则三个球的重量等于( )个正方体的重量
A.2 B.3 C.4 D.5
3.如果,那么x=5成立吗?为什么?
4.若代数式3x+7与x+3互为相反数,求x.
数学广角
利用等式的性质买东西
用5元钱可以买一支钢笔,用2元钱可以买一本笔记本,那么用7元钱就可以买一支钢笔和一本笔记本,15元钱就可以买3支钢笔.相当于: 5元+2元=买1支钢笔的钱+买1本笔记本的钱.3×5元=3×买1支钢笔的钱.”
第三章 一元一次方程
3.2解一元一次方程(一) —合并同类项(第1课时)
学习目标
1.经历运用方程解决实际问题的过程.
2.会运用合并同类项解“”类型的一元一次方程.
3.能够找出实际问题中的已知数和未知数,分析它们之间的数量关系,列出方程.
自主预习
1.合并同类项:
(1) ;
(2) ;
(3) ;
(4) .
2.填空:
(1)( );
(2)+( ).
3.下列各式的合并不正确的是( ).
A.由,得
B.由,得
C.由,得
D.由,得
4.下列各式的变形正确的是( ).
A.
B.
C.
D.
课堂探究
探究一 用合并同类项解方程
某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买的数量又是去年的2倍.前年这个学校购买了几台计算机?
解析:
设前年这个学校购买了x台计算机,则去年购买计算机_____台,今年购买计算机_____台.
问题中的相等关系:
前年购买量+去年购买量+今年购买量=____台
根据题意,列得方程
探究二 规律探究
有一列数,按一定规律排列成1,-3,9,-27,81,-243,……,其中某三个相邻数的和是-1701,这三个数各是多少?
解:设这三个相邻数中第1个数为 ,
则第2个数为 ,第三个数为
根据这三个数的和是-1701,得
归纳:
(1)“合并同类项”解一元一次方程的关键是将方程转化为“”的形式;(2)能将实际问题转化为数学问题,体会“建模”思想和“化归”思想.
重点题型
题型一 解方程
1.解方程(1)
(2)
题型二 列方程解应用题
2.某工厂的产值连续增长,去年是前年的1.5倍,今年是去年的2倍,这三年的总产值为550万元.前年的产值是多少?
随堂训练
1. =3,则=3.
2.三个连续奇数中,2n+1是中间的一个,则另外两个分别是______、_______,他们的和是_________.
3.解下列方程:
(1) ;
(2);
(3);
(4).
能力提升
1.下列合并同类项:①;②;③;④;⑤,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.某厂1月份的产量为吨,2月份比1月份增加2倍,3月份比2月份增加1倍,则该厂第一季度的产量为__________________________;如果第一季度的产量为1800吨,那么1月份的产量为_______________________.
3.一个两位数,个位上的数字是十位上的数字的4倍,它们的和是15,那么这个两位数是多少?
4.把若干糖块分给若干小朋友。若每人3块,则多12块;若每人5块,则少10块.问一共有多少小朋友?多少糖块?
解法1:设一共有x个小朋友,则列方程为__________________,解得x=______
解法2:设一共有y块糖,则列方程为_________________;你会发现此方程有解
数学广角
方程小史
约公元820年,中亚细亚数学家阿尔-花拉子米写了一本代数书,重点论述怎样解方程.这本书的拉丁文译本取名为《对消与还原》.其中“对消”指的就是“合并同类项”.
第三章 一元一次方程
3.2解一元一次方程(一) —合并同类项(第2课时)
学习目标
1.熟练应用合并(同类项)及移项,解“ax+bx=c”“ax+b=cx+d”类型的一元一次方程.
2.进一步感受如何找出实际问题中的已知数和未知数,并分析他们之间的数量关系,列方程.
3.培养自己获取信息、分析问题、处理问题的能力.
自主预习
1.把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
解析:
设这个班有x名学生.
每人分3本,共分出 本,加上剩余的20本,这批书共 本.
每人分4本,需要 本,减去缺少的22本,这批书共 本.
表示这批书的总数的两个代数式________.
由此得方程 _________________________ .
2.解方程时,先移项得 ,再将系数化为1得x= .
3.解下列方程:
(1); (2).
课堂探究
探究一 移项法则
1.如何将方程 3x+20=4x-25 转化为x=a的形式,求出方程的解?该方程与上节课的方程+4x=140从结构上看有何不同?
移项:把等式一边的某项 后移到 ,叫做 .
移项的根据是: .
解方程 3x+20=4x-25 的一般步骤:
解:
移项,得 ——
合并同类项, 得 ——
系数化为1,得 ——
归纳:
解形如ax+b=cx+d的方程步骤是:
① ;② ③ .
自读课本,填写下面的空格
_______
__________________
___________________
2.以上解方程中“移项”起到什么作用?
归纳:
通过移项,含未知数的项与常数项分别位于方程左右两边,使方程更接近于x=a的形式.
探究二 解方程
(1) ;
(2).
探究三 根据实际问题列方程
某制药厂制造一批药品,如果用旧工艺,则废水排量要比环保限制的最大量还多200 t;如果用新工艺,则废水排量要比环保限制的最大量少100 t.新旧工艺的废水排量之比为2 :5,两种工艺的废水排量各是多少?
重点题型
题型一 解方程
1. 解方程:.
题型二 根据实际问题列方程
2.有一个班的同学去划船,他们算了一下,如果增加一条船,正好每条船坐6人,如果送还一条船 ,正好每条船坐9人,问这个班共多少同学?
随堂训练
1.方程的解是
2.关于x的方程3x-7=2x+a的解与方程4x+3=7的解相同,则a的值是
3.下列方程变形中正确的是( )
A 从,得
B 从,得
C从,得
D从,得
4.解下列方程:
(1)
(2)
能力提升
1. 有一些分别标有7,l4,21,28,35,…的卡片,后一张卡片上的数字比前一张卡片上的数字大7,小丽拿了相邻的3张卡片,且这些卡片上的数和为357.(1)猜猜小丽拿的是哪三张卡片 (2)小丽能否拿到相邻的三张卡片,使得三张卡片上的数字之和等于85?若能拿到,请求出是哪三张;若不能,请说明理由.
2.某单位急需要用车但无力购买,他们决定租车使用,某个体出租车司机的条件是:每月付1210元工资,另外每百公里付10元汽油费;另一国营出租车公司的条件是:每百公里付120元.
(1)这个单位若每月平均跑1000千米,租谁的车划算?
(2)求这个单位若每月平均跑多少千米时?租哪家公司的都一样?
数学广角
爱神爱罗斯正在发愁,女神基朴里达问根由:“你为什么烦忧 我亲爱的朋友!”“我在黑里康山采回仙果,路遇缪斯诸神嬉戏抢夺.攸忒皮抢去十二分之一,克里奥拿走五分之一,退里亚取走了八分之一,二十分之一属于麦蓬麦尼,四分之一被忒谱息科里抢走,七分之一到了厄拉托之手,坡力欣尼亚拿的最少,也还有三十个仙果进口,攸累尼亚占了一百二十个,卡来奥皮更有三百个之多,我回家时几乎两手空空,唯有缪斯们留给我的五十个仙果.”请你算一算:爱罗斯当初采摘仙果共多少个
第三章 一元一次方程
3.3.解一元一次方程(二)--去括号与去分母(第1课时)
学习目标
1.会从实际问题中抽象出方程模型,会用一元一次方程解决一些实际问题.
2.理解并掌握去括号解方程的方法.
自主预习
1.某市的出租车收费标准如下:3km以内(含3km)收费8元,超过3km的部分,每千米收费1.5元.收费y(元)与出租车行驶的路程x(km)(x>3)的关系用等式表示为 ;
(1)若小李乘出租车行驶6km,应付车费 元;
(2)若小李付车费17元,则他乘出租车行驶了
千米.
2. 计算:
(1) ;
(2) ;
课堂探究
探究 去括号
1.方程变形成这种变形叫 ,解得 .
2.某车间22名工人生产螺钉和螺母,每人每天平均生产螺钉1 200个或螺母2 000个,一个螺钉要配两个螺母.为了使每天的产品刚好配套,应该分配多少名工人生产螺钉,多少名工人生产螺母?
分析:
1.如果设x名工人生产螺钉,则 名工人生产螺母;
2.为了使每天的产品刚好配套,应使生产的螺母恰好是螺钉数量的 .
解:
归纳:去括号的实质就是乘法分配律的应用
注意:(1)括号前是负号;
(2)括号前系数,在去括号时括号里面的每一项都需要乘以它.
重点题型
题型一 去括号解方程
1.解下列方程:
(1)
(2)
题型二 去括号解实际问题
1.一艘船从甲码头到乙码头顺流而行,用了2h;从乙码头返回甲码头逆流而行,用了2.5h.已知水流的速度是3km/h,求船在静水中的平均速度.
分析:一般情况下可以认为这艘船往返的路程相等,由此填空:
顺流速度 顺流时间 逆流速度 逆流时间
解:
随堂训练
1.去括号:
(1)
(2)
2.小明买了8角与2元的邮票共16枚,花去18元8角.若他买了8角的邮票x枚,可列方程为( )
A.
B.
C.
D.
3.解下列方程:
(1)
(2)
4.学校团委组织65名团员为学校建花坛搬砖,初一同学每人搬6块,其他年级同学每人搬8块,总共搬了400块,问初一同学有多少人参加了搬砖?
能力提升
1.去括号:
(1) ;
(2) = .
2.若,则 .
3.方程去括号正确的是( )
A. B.
C. D.
4.关于的方程的解为,则的值为 ( )
A.6 B. C. D.
5.当 时,的值比的值大1.
中考链接
1.化简结果为( )
A. B. C. D.
2.一群学生前往某电站建设工地进行社会实践活动,男生戴白色安全帽,女生戴红色安全帽.休息时他们坐在一起,大家发现一个有趣的现象,每位男生看到的白色与红色安全帽一样多,而每位女生看到的白色安全帽是红色的2倍.问题:根据这些信息,请你推测这群学生共有多少人?
数学广角
“+”“-”的由来
符号“+”“-”是五百年前一位德国人最先使用的。当时他们并不表示“加上”“减去”。直到三百多年前才正式用来表示“加上”“减去”。
第三章 一元一次方程
3.3.解一元一次方程(二)--去括号与去分母(第2课时)
学习目标
1.通过列方程解决实际问题,逐步建立方程思想.
2.熟练掌握用去分母方法解决一元一次方程.
3.通过去分母解方程,了解数学中的化归思想.
自主预习
1.解一元一次方程的步骤是:
① ②
③ ④
⑤
2.在解方程时,去分母得,
则去分母的根据是 .
3.解方程
去分母得 ,
去括号得 ,
移项得 ,
合并同类项得 .
4.解方程的步骤如下,则错误的一步为 ( ).
A.
B.
C.
D.
课堂探究
探究一 去分母
你能用现有的知识解决下面的问题吗?小组内合作交流,看谁的方法又快又准确.
解下列方程:
归纳:解关于x的方程,就是运用等式性质和运算律,根据方程的特点,逐步转化为 的形式.
探究二 解方程
(1)
解析:去分母(方程两边乘4),得
去括号,得
移项,得
合并同类项,得
系数化为1,得
归纳:
(1)去分母时切记不要漏乘了 的项.
(2)当分子是多项式时,在去分母时要加 .
探究三
一架飞机飞行在两城市之间,已知风速为30
千米/时,顺风飞行要2小时40分钟,逆风飞行要3小时,则两城市之间的距离为多少?
解析:
如果设两城市之间的距离为km,用含的式子表示关于速度的关系:
顺风速度= ÷
逆风速度= ÷
故列方程得:
重点题型
题型一 解有分母的一元一次方程
1.解方程,小数化为整数,得
,去分母得 .
题型二 根据实际问题列方程
2.某人从家骑自行车到火车站,如果每小时行15
千米,那么可以比火车开车时间提前15分钟到达;
如果每小时行9千米,则要比开车时间晚15分钟
到达,则这个人的家到火车站的距离为 ( )千米.
A.11 B.11.25 C.12 D.14
随堂训练
1.如果,则 .
2.解方程得下列结论, 其中正确的是 ( )
A.
B.
C.
D.
3.下列变形中,正确的是 ( )
A.将这个方程变形为
B. 将方程变形为
C. 将方程变形为
D. 将这个方程变形为
4.当 时,互为相反数.
能力提升
1.解方程
(1)
(2)
2.某班组每天需生产50个零件才能在规定的时
间内完成一项生产任务,实际上该班组每天比
计划多生产6个零件,结果比规定时间提前3
天并超额生产了120个零件,若设该班组必须
完成任务为x个,则可列方程为 ( )
A. B.
C. D.
在风速为24km/h的条件下,飞机顺风从A机场
到B机场要用2.8h,它逆风飞行同样的航线要用
3h,求(1)无风时这架飞机在这一航线的平均
航速;(2)两机场之间的航程.
数学广角
家里来了多少客人
小林说:“我没有数,只知道他们每人用一个饭碗,二人合用一个汤碗,三人合用一个菜碗,四人合用一个大酒碗,一共用了15个碗。”你知道来了多少客人吗?
第三章 一元一次方程
3.4实际问题与一元一次方程(第1课时)
学习目标
1.找出实际问题中的数量关系,能根据等量关系列出方程.
2.综合运用数学知识和方法解决简单的实际问题.
自主预习
1.配套问题:
某车间工人生产螺钉和螺母,一个螺钉要配两个螺母,要使生产的产品刚好配套,则应生产的螺母数量恰好是螺钉数量的 倍.
2.工程问题:
(1)工作时间、工作效率、工作量之间的关系:
工作量= × ;
工作时间= ÷ ;
工作效率= ÷ .
(2)通常设完成全部工作的总工作量为 ,如果一项工作分几个阶段完成,那么各阶段工作量的和= ,这是常见的列方程的依据.
(3)一项工作,甲用a小时完成,则甲的工作量可看成 ,工作时间是 ,工作效率 ,
若这项工作乙用b小时完成,则乙的工作效率
工作时间是 .
3.一件工作,甲独做10小时完成,乙独做8小时完成,现在先由甲独做1小时,余下的由甲乙一起完成,余下的部分需要几小时完成?若设余下 的部分需要x小时完成,则由此条件可列方程得:
.
课堂探究
探究一 配套问题
1. 某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
分析
问题1:设适当的未知数,填写下表:
工人总数 每名工人每天生产螺钉个数 每名工人每天生产螺母个数 分配生产螺钉的工人人数 分配生产螺母的工人人数 工人生产的螺钉的总个数 工人生产的螺母的总个数
问题2:要使每天生产的螺钉和螺母配套,则他们个数之间存在着怎样的数量关系?
问题3:本题的数量关系是什么?
探究二 工程问题
2.整理一批图书,由一个人做要40 h完成.现在计划由一部分人先做4 h,再增加2人和他们一起做8 h,完成这项工作.假设这些人的工作效率相同,具体事先安排多少人工作?
分析:
问题1:设适当的未知数,填写下表:
工作总量 每个人的工作效率 先安排的人数 先安排的人4h完成的工作量 增加后的人数 增加人数后8h完成的工作量
问题2:本题的数量关系是什么?
问题3:本题还有没有另外列方程的方法?
归纳:用方程解实际问题的基本过程
审 :借助表格,图表等提炼数学信息,理解问题中的基本数学关系;
设:用代数式表示实际问题中的文字语言,文字语言符号化;
列:找到所列代数式中的基本等量关系,列出方程;
解 :数学方程的解;
验:数学方程的解,实际问题有意义;
答 :实际问题的答案.
重点题型
题型一 用一元一次方程解决配套问题
1.某纺织厂有纺织工人300名,为增产创收,该纺织厂又增设了制衣车间,准备将这300名纺织工人合理分配到纺织车间和制衣车间.现在知道工人每人每天平均能织布30米或制4件成衣,每件成衣用布1.5米,若使生产出的布匹刚好制成成衣,问应有多少人去生产制衣,多少人去纺织?
题型二 用一元一次方程解决工程问题
2.一项工程,估计若由一个人完成需要40天. 现在若2人先做4天,再增加2人和他们一起做,可以完成这项工程. 假设这些人的工作效率相同,那么完成这项工程共用多少天?
题型三 用一元一次方程解决人员调配问题
3.在甲处工作的有272人,在乙处工作的由196人,如果使乙处的人数是甲处工作人数的,应从乙处调多少人到甲处?
随堂训练
一套仪器有一个A部件和三个B部件构成.用1m3钢材可做40个A部件或240个B部件.现要用6m3钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
中考链接
(2012·贵州铜仁)铜仁市对城区主干道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完.设原有树苗x棵,则根据题意列出方程正确的是( )
A. B.
C. D.
数学广角
阿拉伯数字的由来
阿拉伯数字实际是印度人发明的。大约在1500年以前,印度人就已经用一种特殊的字来表示数目,这些字有10个,只要一笔两笔就可以写成。后来,由于各国之间的接触,这些数字传入阿拉伯,阿拉伯人觉得它们很简单,于是在自己的国家开始广泛使用并且把他传到全欧洲。就这样,它们慢慢地就成了我们今天使用的数字。因为阿拉伯人在传播这种数字方面,起的作用很大,人们也就习惯了称这种数字为‘阿拉伯数字
第三章 一元一次方程
3.4 实际问题与一元一次方程(第2课时)
学习目标
1.会根据销售问题中数量关系列方程解决问题,熟练掌握一元一次方程的解法.
2.培养学生数学建模能力,分析问题、解决问题的能力.
3. 通过开放性问题的设计,培养学生创新能力和挑战自我的意识,增强学生的学习兴趣;
自主预习
1. 列一元一次方程解决实际问题的一般步骤包括:
(1)_______;(2)______;(3)_______;
(4)_______;(5)________;(6)_________.
2.解方程:
(1);
(2).
3.销售问题中的等量关系:
(1)售价=标价×__________;
(2)利润率=____________×100%;
(3)利润=______-_______=_______×________.
(利润的两种表示方法是列方程的等量关系)
课堂探究
探究 销售中的盈亏
某商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
分析:
1.如何判断盈利还是亏损?
2.完成下表:
商品 售价/元 进价/元 利润/元 利润率 利润/元
第一件 60 x 盈利25%
第二件 60 y 亏损25%
3.等量关系:
4.列方程解决问题:
归纳:
一般地,当两件商品的售价相同,盈利和亏损率也相同时,总的盈亏情况具有相同的规律吗?
重点题型
题型一 打折销售
1.某商品的售价为每件900元,为了参与市场竞争,商品按售价的9折再让利40元销售,此时仍可获利10%,此商品的进价是多少元?
题型二 销售中的盈亏
2.某商场为减少库存积压,以每件120元的价格出售两件夹克上衣,其中一件盈利20%,另一件亏损20%,在这次买卖中商场是盈利还是亏损,或是不盈不亏?
随堂训练
1.某面粉仓库存放的面粉运出 15%后,还剩余42 500千克,这个仓库原来有多少面粉?
2.小张自主创业开了一家服装店,因为进货时没有进行市场调查,在换季时积压了一批服装.为了缓解资金的压力,小张决定打折出售.若每件服装按标价的5折出售将亏20元,而按标价的8折出售将赚40元.请你算一算每件服装标价多少元?每件服装成本是多少元?
中考链接
(2012·湖南娄底)体育文化用品商店购进篮球和排球共20个,进价和售价如表,全部销售完后共获利润260元.
(1)购进篮球和排球各多少个?
(2)销售6个排球的利润与销售几个篮球的利润相等?
数学广角
一个故事引发的数学家
陈景润一个家喻户晓的数学家,在攻克歌德巴赫猜想方面作出了重大贡献,创立了著名的“陈氏定理”,所以有许多人亲切地称他为“数学王子”。但有谁会想到,他的成就源于一个故事。 1937年,勤奋的陈景润考上了福州英华书院,此时正值抗日战争时期,清华大学航空工程系主任留英博士沈元教授回福建奔丧,不想因战事被滞留家乡。几所大学得知消息,都想邀请沈教授前进去讲学,他谢绝了邀请。由于他是英华的校友,为了报达母校,他来到了这所中学为同学们讲授数学课。 一天,沈元老师在数学课上给大家讲了一故事:“200年前有个法国人发现了一个有趣的现象:6=3+3,8=5+3,10=5+5,12=5+7,28=5+23,100=11+89。每个大于4的偶数都可以表示为两个奇数之和。因为这个结论没有得到证明,所以还是一个猜想。大数学欧拉说过:虽然我不能证明它,但是我确信这个结论是正确的。
第三章 一元一次方程
3.4实际问题与一元一次方程(第3课时)
学习目标
1.在实际问题的探究过程中,弄清问题背景,分析清楚有关数量关系,正确找出列方程所依据的主要相等关系.
2.能根据球赛积分问题中的数量关系,列出一元一次方程,体会方程是刻画现实世界的一个有效的数学模型.
自主预习
1.下表是某年中超联赛中A、B、C、D、E五支球队的积分及胜负情况:
队名 场次 胜场 平场 负场 积分
A 16 8 4 4 28
B 16 0 16 0 16
C 16 0 12 4 12
D 16 5 8 3 a
E 16 b c 2 26
(1)从B队积分可以看出,平一场积 分;
(2)从C队积分可以看出,负一场积 分;
(3)再从A队积分可以看出,胜一场积 分;
(4)观察D、E队提供的信息,可得a= ,
b= ,c= .
2.一次数学小测验共有25道选择题,评分标准如下:答对1题得4分;答错l题扣l分;不答得0 分.已知小明不答的题比答错的题多2道,他的总分是74分,则他答对了多少道题?
课堂探究
探究 球赛积分表问题
下表是某次篮球联赛积分榜:
队名 比赛场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
(1)用式子表示总积分与胜、负场数之间的数量关系;
(2)某队的胜场积分能等于它的负场总积分吗?
分析:
1.表中各队所得积分不同,但各队计算积分的方法是否一样?如果一样,如何计算积分?
2.列式之前要先弄清楚哪几个量?
3.通过观察积分表,选择哪一行的的数据最与众不同?由这一行能看出我们需要的哪个数据?
4.如何计算胜一场积多少分?
5.胜、负一场的积分数都已确定,由于各队胜、负场数各不相同,因此各队积分也不相同,如何在这一个问题中同时表示出这三个变量呢?它们之间是否存在什么不变的关系呢?
重点题型
题型 球赛积分问题
下表是我国2012年中超积分榜情况(截至5月19日).
排名 球队 胜 平 负 积分
1 广州恒大 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 7 1 2 22
2 广州富力 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 7 0 3 21
3 江苏舜天 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 5 3 2 18
4 北京国安 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 5 3 2 18
5 长春亚泰 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 4 3 2 15
6 杭州绿城 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 4 3 4 15
7 贵州人和 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 3 5 2 14
8 天津泰达 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 4 1 5 13
9 大连实德 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 3 3 4 12
10 上海申鑫 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 3 2 6 11
11 辽宁宏运 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 2 5 3 11
12 上海申花 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 2 5 3 11
13 大 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank )连阿尔滨 2 4 4 10
14 河南建业 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 3 1 6 10
15 山东鲁能 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 2 3 4 9
16 青岛中能 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 2 2 6 8
根据以上情况,解决下列问题:
(1)足球比赛中胜一场,平一场,负一场各得多少分?
(2)假设广州恒大赛了30场,负了2场,那么它的积分能为45分吗?请说明理由.
随堂训练
1.郑逸同学是学校的篮球明星,在一场篮球比赛中,他一人得了23分,如果他投进的2分球比3分球多4个,那么他一共投进了( )个2分球.
A.3 B.7 C.4 D.8
2.足球比赛的计分规则为:胜一场得3分,平一场得1分,负一场得0分.一支队踢了14场,负5场,共得l9分,那么这支队胜了 ( )
A.3场 B.4场 C.5场 D.6场
3.为了迎接2010年世界杯足球赛的到来,某足球协会举办了一次足球赛,其记分规则及奖励方案(每人)如下表:当比赛进行到每队各比赛l2场时,A队(11名队员)共积20分,并且没有负一场.
(1)试判断A队胜、平各几场;
(2)若每赛一场每名队员均得出场费500元,那么A 队的某一名队员所得奖金与出场费的和是多少元
能力提升
足球比赛的计分规则为:胜一场得3分,平一场得1分,输一场得O分.一支足球队在某个赛季中共需比赛l4场,现已比赛了8场,输了l场,得17分.请问:
(1)前8场比赛中,这支球队共胜了多少场
(2)这支球队打满l4场比赛,最高能得多少分
(3)通过对比赛情况的分析,这支球队打满l4场比赛,得分不低于29分,就可以达到预期目标,请你分析一下,在后面的6场比赛中,这支球队至少要胜几场才能达到预期目标
数学广角
数学家的遗嘱
阿拉伯数学家花拉子密的遗嘱,当时他的妻子正怀着他们的第一胎小孩。“如果我亲爱的妻子帮我生个儿子,我的儿子将继承三分之二的遗产,我的妻子将得三分之一;如果是生女的,我的妻子将继承三分之二的遗产,我的女儿将得三分之一。” 而不幸的是,在孩子出生前,这位数学家就去世了。之后,发生的事更困扰大家,他的妻子帮他生了一对龙凤胎,而问题就发生在他的遗嘱内容。
如何遵照数学家的遗嘱,将遗产分给他的妻子、儿子、女儿呢?
第三章 一元一次方程
3.4实际问题与一元一次方程(第4课时)
学习目标
1.掌握一元一次方程的解法,熟悉用一元一次方程解应用题的基本步骤.
2.经历把实际问题模型化的过程,体会方程思想的作用.
3.通过具体情境引入本节课(电话计费问题),使学生感受数学的魅力和作用.
自主预习
为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.
该市自来水收费价格见价目表:
价 目 表
每月用水 单 价
不超出6m3的部分 2元/ m3
超出6m3不超出10m3的部分 4元/ m3
超出10m3的部分 8元/ m3
(1)若某户居民1月份用水8m3,则应收水费:
____________元;
(2)若某户居民2月份用水12.5m3,则应收水费________元;
(3)若某户居民3、4月份共用水15m3(4月份用水量超过3月份),共交水费44元,则该户居民3、4月份各用水多少m3?
课堂探究
电话计费问题
下表中有两种移动电话计费方式
考虑下列问题:
(1) 设一个月内用移动电话主叫为t min(t是正整数),根据上表说明:当t在不同时间范围内取值时,按方式一和方式二如何计费.
(2) 你能从中发现如何根据主叫时间选择省钱的计费方式吗?
1.你能解读方式一中是如何计费的吗?方式二呢?
2.在方式一中,计费与什么有关?方式二中呢?
3.小明一个月主叫时间100 min,按方式一和方式二计费,哪个计费少?200 min呢?300 min 呢?是否存在一个时间t,两种方式计费一样多呢?你能列出方程吗?
重点题型
题型 纳税问题
2005年10月27日全国人大通过《关于修改<中华人民共和国个人所得税>的决定》,征收个人所
得税的起点从800元提高到1 600元,也就是说,原来月收入超过800元的部分为全月应纳税所得额,从2006年1月1日起,月收入超过1 600元的部分为全月应纳税所得额. 税法修改前后全月应纳税所得额的划分及相应的税率相同,见下表:
全月应纳税所得额 税率(%)
不超过500元的部分 5
超过500至2 000元的部分 10
超过2 000至5 000元的部分 15
… …
某人2005年12月依法缴纳本月个人所得税115元,假如本月按新税法计算,此人应少纳税多少元?
随堂训练
1.中国移动某分公司开设适合普通用户的两种通讯业务,分别是:
“龙城通”用户先缴25元月租,然后每分钟通话费用0.2元;“神州行”用户不用缴纳月租费,每分钟通话费用0.4元. (通话均指拨打本地电话)
(1)一个月内通话多少分钟,两种移动通讯方式费用相同?
(2)若李老师一个月通话约80分钟,请你给他提个建议,应选择哪种移动通讯方式合算一些?请说明理由.
中考链接
(2012 天津中考)某通讯公司推出了移动电话的两种计费方式(详情见下表).
温馨提示:若选方式一,每月固定缴费58元,当主动打出的电话月累计不超过150分,不再额外缴费;当超过150分,超过部分每分钟加收0.25元.
设一个月内使用移动电话主叫的时间为t分(t为正整数),请根据表中提供的信息回答下列问题:
(1)用含有t的式子填写下表:
(2)当t为何值时,两种计费方式的费用相等?
(3)当330<t<360时,你认为选用哪种计费方式省钱(直接写出结果即可)
这批书的总数有几种表示法?它们之间有什么关系?
3.1.1一元一次方程
学习目标
1.了解等式与方程的区别与联系.
2.掌握一元一次方程、方程的解及解方程的有关概念.
3.通过算术法和列方程的比较,体会从算式到方程的进步.
自主预习
1.一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70km/h,卡车的行驶速度是60km/h客车比卡车早1h经过B地.A,B两地间的路程是多少?
(1)用算术法解决这个问题;
(2)用方程表示该问题(只列方程不解).
2.根据下列问题,设未知数并列出方程:
(1)用一根长24cm的铁丝围成一个正方形,正方形的边长是多少?
(2)一台计算机已使用1700小时,预计每月再使用150小时,经过多少月这台计算机的使用时间达到规定的检修时间2450小时?
(3)某校女生占全体学生数的52%,比男生多80人,这个学校有多少学生?
3.观察下列式子:①7+3=10;②3x-5=1;③5x-2x;④2x-l≠x;⑤x-1=7;⑥=3.其中 是等式, 是方程; 是一元一次方程(填序号).
4.括号里的数(x=3,x=4,x=-4)是x(x+1)=12的解的有 .
课堂探究
探究一 等式与方程
1.___________________________________叫等式;_________________________________叫方程.
2.式子①②③④ ⑤⑥⑦中等式是________________________;
方程是___________________________.
归纳:
等式与方程的区别与联系:
探究二 一元一次方程
观察下列方程,你能说出它们的共同特征吗?
① ②
③④
归纳:
只含有_______个未知数,未知数的次数都是_______,等号两边都是_______,这样的方程叫做一元一次方程.
探究三 解方程与方程的解
1.解方程的定义:
2.方程的解的定义:
重点题型
题型一 一元一次方程的概念
1.下列各式中①② ③ ④是一元一次方程的是_______.
2.已知方程是一元一次方程,则n=_______.
3.是关于x 的一元一次方程,则k=_________
题型二 方程的解
4.已知是方程的解,则m=_________.
5.写出一个以为解的一元一次方程_______________________.
随堂训练
1.下列方程:①x-1=5;②-x=;③=5;④x(x+1)=2;⑤4-2x=x+1中是一元一次方程是( )
A.①② B.①②③
C.①②③⑤ D.①②⑤
2.已知(2m-3)x-(2-3m)x=1是关于x的一元一次方程,则m=_______.
3.请写出一个解为2的关于x的一元一次方程: .
4.已知x的2倍与2x-4的值互为相反数,则可列方程为 .
5.一个两位数,十位上数字为a,个位数字比a大2,且十位上数与个位上数和为6,列方程为________.
6.检验方程后面大括号内所列各数是否为前面方程的解: =2x-l,{2,-5}.
7.只列出方程:
(1)小明买了4个笔记本和3支圆珠笔一共用了4.7元,已知笔记本每本0.8元,圆珠笔每支多少元?
(2)甲、乙两个运输队,甲队32人,乙队28人,若从乙队调走若干人到甲队,那么甲队人数恰好是乙队人数的2倍,求从乙队调走多少人到甲队?
能力提升
1.已知是关于x的一元一次方程,求k的值.
2.七年级一班的一个综合实践活动小组去A、B两个超市调查去年和今年五一期间的销售情况,如图是调查后小敏与其他两位同学进行交流的情景,根据他们的对话,求A、B两个超市今年五一期问的销售额(只列方程).
3.在一次植树活动中,甲班植树的株数比乙班多20%,乙班植树的株树比甲班的一半多10株.设乙班植树x株.
(1)列两个不同的含x的代数式,分别表示甲班植树的株数;
(2)根据题意列出含未知数x的方程;
(3)检验乙班、甲班植树株数是不是分别为25株和35株.
数学广角
方程小史
“方程”一词来源于我国古算书《九章算术》.在这部著作中,已经会列一元一次方程.
宋元时期,中国数学家创立了“天元术”,用天元表示未知数进而建立方程.这种方法的代表作是数学家李冶写的《测圆海镜》书中所说的“立天元一”相当于现在的“设未知数x”.
清代数学家李善兰翻译外国数学著作时,开始将equation一词译为“方程”,至今一直这样沿用.
第三章 一元一次方程
3.1.2 等式的性质
学习目标
1.掌握等式的两条性质.
2.会用等式的性质解简单的一元一次方程.
3.初步具有解方程中的化归意识.
自主预习
1.如果a=b,那么ac= ;
如果a=b(c≠O),那么= .
2.说出下列各式变形的根据.
(1)由2a+5-a,
得2a-a+5.( )
(2)由-2x=8,
得x=-4.( )
(3)由3x=2+2x,
得x=2.( )
(4)由-x=2,
得x=-6.( )
3.利用等式的性质解方程:
(1)x+5=13;
(2)-x-3=5.
课堂探究
探究一 等式的性质
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡.
1.如图,由左边天平到右边天平或由右边天平到左边天平发生怎样的变化?你发现了什么事实?
归纳:
等式性质1: 等式两边加(或减)__________,结果_____________.
用字母表示为:如果________,那么______.
2.如图,由左边天平到右边天平或由右边天平到左边天平发生怎样的变化?你发现了什么事实?
归纳:
等式性质2: 等式两边同乘一个数或除__________结果______________.
用字母表示为:如果________,那么________ 如果________,那么________.
3.下列运用等式的性质对等式进行的变形中,正确的是( ).
A.由3+x=5,得x=5+3 B.由7x=-4,得x=-
C.由y=0,得y=2 D.由3=x-2,得-x=-2-3
探究二 利用等式的性质解方程
利用等式的性质解方程:
(1)x+7=26;
(2)-5x=20;
(3)- x-5=4.
重点题型
题型 等式性质的应用
1.用适当的数或字母填空,使所得结果仍是等式.
(1)如果x-5=-1,那么x= ;
(2)如果,那么a= ;
(3)如果-2x=8,那么x= ;
(4)如果2x-3=3x,那么x= .
2.已知m+a=n+b,根据等式性质变形为m=n,那么a,b必须满足的条件是 ( )
A.a=-b B.-a=b
C.a=b D.a,b可以是任意整式
3. 如果ma=mb,那么下列等式中,不一定成立的是( )
A.ma+1=mb+1 B.ma-3=mb-3
C.-2ma=-2mb D.a=b
随堂训练
1.用适当的数或字母填空,使所得结果仍是等式.
(1)如果那么 ;
(2)如果那么 .
2.下列各式变形正确的是( )
A.由
B.由
C.由
D.由
3.已知根据等式性质变形
那么必须满足的条件是( )
A. B.
C. D.可以是任意整式
4.由,得,其依据是 .
5.用等式的性质解释下列方程:
.
能力提升
1. 下列变形不正确的是 ( )
A.若2R=2r (0),得R=r
B.若a=b,则
C.若,则
D.若,得
2.如图所示,两个天平都平衡,则三个球的重量等于( )个正方体的重量
A.2 B.3 C.4 D.5
3.如果,那么x=5成立吗?为什么?
4.若代数式3x+7与x+3互为相反数,求x.
数学广角
利用等式的性质买东西
用5元钱可以买一支钢笔,用2元钱可以买一本笔记本,那么用7元钱就可以买一支钢笔和一本笔记本,15元钱就可以买3支钢笔.相当于: 5元+2元=买1支钢笔的钱+买1本笔记本的钱.3×5元=3×买1支钢笔的钱.”
第三章 一元一次方程
3.2解一元一次方程(一) —合并同类项(第1课时)
学习目标
1.经历运用方程解决实际问题的过程.
2.会运用合并同类项解“”类型的一元一次方程.
3.能够找出实际问题中的已知数和未知数,分析它们之间的数量关系,列出方程.
自主预习
1.合并同类项:
(1) ;
(2) ;
(3) ;
(4) .
2.填空:
(1)( );
(2)+( ).
3.下列各式的合并不正确的是( ).
A.由,得
B.由,得
C.由,得
D.由,得
4.下列各式的变形正确的是( ).
A.
B.
C.
D.
课堂探究
探究一 用合并同类项解方程
某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买的数量又是去年的2倍.前年这个学校购买了几台计算机?
解析:
设前年这个学校购买了x台计算机,则去年购买计算机_____台,今年购买计算机_____台.
问题中的相等关系:
前年购买量+去年购买量+今年购买量=____台
根据题意,列得方程
探究二 规律探究
有一列数,按一定规律排列成1,-3,9,-27,81,-243,……,其中某三个相邻数的和是-1701,这三个数各是多少?
解:设这三个相邻数中第1个数为 ,
则第2个数为 ,第三个数为
根据这三个数的和是-1701,得
归纳:
(1)“合并同类项”解一元一次方程的关键是将方程转化为“”的形式;(2)能将实际问题转化为数学问题,体会“建模”思想和“化归”思想.
重点题型
题型一 解方程
1.解方程(1)
(2)
题型二 列方程解应用题
2.某工厂的产值连续增长,去年是前年的1.5倍,今年是去年的2倍,这三年的总产值为550万元.前年的产值是多少?
随堂训练
1. =3,则=3.
2.三个连续奇数中,2n+1是中间的一个,则另外两个分别是______、_______,他们的和是_________.
3.解下列方程:
(1) ;
(2);
(3);
(4).
能力提升
1.下列合并同类项:①;②;③;④;⑤,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.某厂1月份的产量为吨,2月份比1月份增加2倍,3月份比2月份增加1倍,则该厂第一季度的产量为__________________________;如果第一季度的产量为1800吨,那么1月份的产量为_______________________.
3.一个两位数,个位上的数字是十位上的数字的4倍,它们的和是15,那么这个两位数是多少?
4.把若干糖块分给若干小朋友。若每人3块,则多12块;若每人5块,则少10块.问一共有多少小朋友?多少糖块?
解法1:设一共有x个小朋友,则列方程为__________________,解得x=______
解法2:设一共有y块糖,则列方程为_________________;你会发现此方程有解
数学广角
方程小史
约公元820年,中亚细亚数学家阿尔-花拉子米写了一本代数书,重点论述怎样解方程.这本书的拉丁文译本取名为《对消与还原》.其中“对消”指的就是“合并同类项”.
第三章 一元一次方程
3.2解一元一次方程(一) —合并同类项(第2课时)
学习目标
1.熟练应用合并(同类项)及移项,解“ax+bx=c”“ax+b=cx+d”类型的一元一次方程.
2.进一步感受如何找出实际问题中的已知数和未知数,并分析他们之间的数量关系,列方程.
3.培养自己获取信息、分析问题、处理问题的能力.
自主预习
1.把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
解析:
设这个班有x名学生.
每人分3本,共分出 本,加上剩余的20本,这批书共 本.
每人分4本,需要 本,减去缺少的22本,这批书共 本.
表示这批书的总数的两个代数式________.
由此得方程 _________________________ .
2.解方程时,先移项得 ,再将系数化为1得x= .
3.解下列方程:
(1); (2).
课堂探究
探究一 移项法则
1.如何将方程 3x+20=4x-25 转化为x=a的形式,求出方程的解?该方程与上节课的方程+4x=140从结构上看有何不同?
移项:把等式一边的某项 后移到 ,叫做 .
移项的根据是: .
解方程 3x+20=4x-25 的一般步骤:
解:
移项,得 ——
合并同类项, 得 ——
系数化为1,得 ——
归纳:
解形如ax+b=cx+d的方程步骤是:
① ;② ③ .
自读课本,填写下面的空格
_______
__________________
___________________
2.以上解方程中“移项”起到什么作用?
归纳:
通过移项,含未知数的项与常数项分别位于方程左右两边,使方程更接近于x=a的形式.
探究二 解方程
(1) ;
(2).
探究三 根据实际问题列方程
某制药厂制造一批药品,如果用旧工艺,则废水排量要比环保限制的最大量还多200 t;如果用新工艺,则废水排量要比环保限制的最大量少100 t.新旧工艺的废水排量之比为2 :5,两种工艺的废水排量各是多少?
重点题型
题型一 解方程
1. 解方程:.
题型二 根据实际问题列方程
2.有一个班的同学去划船,他们算了一下,如果增加一条船,正好每条船坐6人,如果送还一条船 ,正好每条船坐9人,问这个班共多少同学?
随堂训练
1.方程的解是
2.关于x的方程3x-7=2x+a的解与方程4x+3=7的解相同,则a的值是
3.下列方程变形中正确的是( )
A 从,得
B 从,得
C从,得
D从,得
4.解下列方程:
(1)
(2)
能力提升
1. 有一些分别标有7,l4,21,28,35,…的卡片,后一张卡片上的数字比前一张卡片上的数字大7,小丽拿了相邻的3张卡片,且这些卡片上的数和为357.(1)猜猜小丽拿的是哪三张卡片 (2)小丽能否拿到相邻的三张卡片,使得三张卡片上的数字之和等于85?若能拿到,请求出是哪三张;若不能,请说明理由.
2.某单位急需要用车但无力购买,他们决定租车使用,某个体出租车司机的条件是:每月付1210元工资,另外每百公里付10元汽油费;另一国营出租车公司的条件是:每百公里付120元.
(1)这个单位若每月平均跑1000千米,租谁的车划算?
(2)求这个单位若每月平均跑多少千米时?租哪家公司的都一样?
数学广角
爱神爱罗斯正在发愁,女神基朴里达问根由:“你为什么烦忧 我亲爱的朋友!”“我在黑里康山采回仙果,路遇缪斯诸神嬉戏抢夺.攸忒皮抢去十二分之一,克里奥拿走五分之一,退里亚取走了八分之一,二十分之一属于麦蓬麦尼,四分之一被忒谱息科里抢走,七分之一到了厄拉托之手,坡力欣尼亚拿的最少,也还有三十个仙果进口,攸累尼亚占了一百二十个,卡来奥皮更有三百个之多,我回家时几乎两手空空,唯有缪斯们留给我的五十个仙果.”请你算一算:爱罗斯当初采摘仙果共多少个
第三章 一元一次方程
3.3.解一元一次方程(二)--去括号与去分母(第1课时)
学习目标
1.会从实际问题中抽象出方程模型,会用一元一次方程解决一些实际问题.
2.理解并掌握去括号解方程的方法.
自主预习
1.某市的出租车收费标准如下:3km以内(含3km)收费8元,超过3km的部分,每千米收费1.5元.收费y(元)与出租车行驶的路程x(km)(x>3)的关系用等式表示为 ;
(1)若小李乘出租车行驶6km,应付车费 元;
(2)若小李付车费17元,则他乘出租车行驶了
千米.
2. 计算:
(1) ;
(2) ;
课堂探究
探究 去括号
1.方程变形成这种变形叫 ,解得 .
2.某车间22名工人生产螺钉和螺母,每人每天平均生产螺钉1 200个或螺母2 000个,一个螺钉要配两个螺母.为了使每天的产品刚好配套,应该分配多少名工人生产螺钉,多少名工人生产螺母?
分析:
1.如果设x名工人生产螺钉,则 名工人生产螺母;
2.为了使每天的产品刚好配套,应使生产的螺母恰好是螺钉数量的 .
解:
归纳:去括号的实质就是乘法分配律的应用
注意:(1)括号前是负号;
(2)括号前系数,在去括号时括号里面的每一项都需要乘以它.
重点题型
题型一 去括号解方程
1.解下列方程:
(1)
(2)
题型二 去括号解实际问题
1.一艘船从甲码头到乙码头顺流而行,用了2h;从乙码头返回甲码头逆流而行,用了2.5h.已知水流的速度是3km/h,求船在静水中的平均速度.
分析:一般情况下可以认为这艘船往返的路程相等,由此填空:
顺流速度 顺流时间 逆流速度 逆流时间
解:
随堂训练
1.去括号:
(1)
(2)
2.小明买了8角与2元的邮票共16枚,花去18元8角.若他买了8角的邮票x枚,可列方程为( )
A.
B.
C.
D.
3.解下列方程:
(1)
(2)
4.学校团委组织65名团员为学校建花坛搬砖,初一同学每人搬6块,其他年级同学每人搬8块,总共搬了400块,问初一同学有多少人参加了搬砖?
能力提升
1.去括号:
(1) ;
(2) = .
2.若,则 .
3.方程去括号正确的是( )
A. B.
C. D.
4.关于的方程的解为,则的值为 ( )
A.6 B. C. D.
5.当 时,的值比的值大1.
中考链接
1.化简结果为( )
A. B. C. D.
2.一群学生前往某电站建设工地进行社会实践活动,男生戴白色安全帽,女生戴红色安全帽.休息时他们坐在一起,大家发现一个有趣的现象,每位男生看到的白色与红色安全帽一样多,而每位女生看到的白色安全帽是红色的2倍.问题:根据这些信息,请你推测这群学生共有多少人?
数学广角
“+”“-”的由来
符号“+”“-”是五百年前一位德国人最先使用的。当时他们并不表示“加上”“减去”。直到三百多年前才正式用来表示“加上”“减去”。
第三章 一元一次方程
3.3.解一元一次方程(二)--去括号与去分母(第2课时)
学习目标
1.通过列方程解决实际问题,逐步建立方程思想.
2.熟练掌握用去分母方法解决一元一次方程.
3.通过去分母解方程,了解数学中的化归思想.
自主预习
1.解一元一次方程的步骤是:
① ②
③ ④
⑤
2.在解方程时,去分母得,
则去分母的根据是 .
3.解方程
去分母得 ,
去括号得 ,
移项得 ,
合并同类项得 .
4.解方程的步骤如下,则错误的一步为 ( ).
A.
B.
C.
D.
课堂探究
探究一 去分母
你能用现有的知识解决下面的问题吗?小组内合作交流,看谁的方法又快又准确.
解下列方程:
归纳:解关于x的方程,就是运用等式性质和运算律,根据方程的特点,逐步转化为 的形式.
探究二 解方程
(1)
解析:去分母(方程两边乘4),得
去括号,得
移项,得
合并同类项,得
系数化为1,得
归纳:
(1)去分母时切记不要漏乘了 的项.
(2)当分子是多项式时,在去分母时要加 .
探究三
一架飞机飞行在两城市之间,已知风速为30
千米/时,顺风飞行要2小时40分钟,逆风飞行要3小时,则两城市之间的距离为多少?
解析:
如果设两城市之间的距离为km,用含的式子表示关于速度的关系:
顺风速度= ÷
逆风速度= ÷
故列方程得:
重点题型
题型一 解有分母的一元一次方程
1.解方程,小数化为整数,得
,去分母得 .
题型二 根据实际问题列方程
2.某人从家骑自行车到火车站,如果每小时行15
千米,那么可以比火车开车时间提前15分钟到达;
如果每小时行9千米,则要比开车时间晚15分钟
到达,则这个人的家到火车站的距离为 ( )千米.
A.11 B.11.25 C.12 D.14
随堂训练
1.如果,则 .
2.解方程得下列结论, 其中正确的是 ( )
A.
B.
C.
D.
3.下列变形中,正确的是 ( )
A.将这个方程变形为
B. 将方程变形为
C. 将方程变形为
D. 将这个方程变形为
4.当 时,互为相反数.
能力提升
1.解方程
(1)
(2)
2.某班组每天需生产50个零件才能在规定的时
间内完成一项生产任务,实际上该班组每天比
计划多生产6个零件,结果比规定时间提前3
天并超额生产了120个零件,若设该班组必须
完成任务为x个,则可列方程为 ( )
A. B.
C. D.
在风速为24km/h的条件下,飞机顺风从A机场
到B机场要用2.8h,它逆风飞行同样的航线要用
3h,求(1)无风时这架飞机在这一航线的平均
航速;(2)两机场之间的航程.
数学广角
家里来了多少客人
小林说:“我没有数,只知道他们每人用一个饭碗,二人合用一个汤碗,三人合用一个菜碗,四人合用一个大酒碗,一共用了15个碗。”你知道来了多少客人吗?
第三章 一元一次方程
3.4实际问题与一元一次方程(第1课时)
学习目标
1.找出实际问题中的数量关系,能根据等量关系列出方程.
2.综合运用数学知识和方法解决简单的实际问题.
自主预习
1.配套问题:
某车间工人生产螺钉和螺母,一个螺钉要配两个螺母,要使生产的产品刚好配套,则应生产的螺母数量恰好是螺钉数量的 倍.
2.工程问题:
(1)工作时间、工作效率、工作量之间的关系:
工作量= × ;
工作时间= ÷ ;
工作效率= ÷ .
(2)通常设完成全部工作的总工作量为 ,如果一项工作分几个阶段完成,那么各阶段工作量的和= ,这是常见的列方程的依据.
(3)一项工作,甲用a小时完成,则甲的工作量可看成 ,工作时间是 ,工作效率 ,
若这项工作乙用b小时完成,则乙的工作效率
工作时间是 .
3.一件工作,甲独做10小时完成,乙独做8小时完成,现在先由甲独做1小时,余下的由甲乙一起完成,余下的部分需要几小时完成?若设余下 的部分需要x小时完成,则由此条件可列方程得:
.
课堂探究
探究一 配套问题
1. 某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
分析
问题1:设适当的未知数,填写下表:
工人总数 每名工人每天生产螺钉个数 每名工人每天生产螺母个数 分配生产螺钉的工人人数 分配生产螺母的工人人数 工人生产的螺钉的总个数 工人生产的螺母的总个数
问题2:要使每天生产的螺钉和螺母配套,则他们个数之间存在着怎样的数量关系?
问题3:本题的数量关系是什么?
探究二 工程问题
2.整理一批图书,由一个人做要40 h完成.现在计划由一部分人先做4 h,再增加2人和他们一起做8 h,完成这项工作.假设这些人的工作效率相同,具体事先安排多少人工作?
分析:
问题1:设适当的未知数,填写下表:
工作总量 每个人的工作效率 先安排的人数 先安排的人4h完成的工作量 增加后的人数 增加人数后8h完成的工作量
问题2:本题的数量关系是什么?
问题3:本题还有没有另外列方程的方法?
归纳:用方程解实际问题的基本过程
审 :借助表格,图表等提炼数学信息,理解问题中的基本数学关系;
设:用代数式表示实际问题中的文字语言,文字语言符号化;
列:找到所列代数式中的基本等量关系,列出方程;
解 :数学方程的解;
验:数学方程的解,实际问题有意义;
答 :实际问题的答案.
重点题型
题型一 用一元一次方程解决配套问题
1.某纺织厂有纺织工人300名,为增产创收,该纺织厂又增设了制衣车间,准备将这300名纺织工人合理分配到纺织车间和制衣车间.现在知道工人每人每天平均能织布30米或制4件成衣,每件成衣用布1.5米,若使生产出的布匹刚好制成成衣,问应有多少人去生产制衣,多少人去纺织?
题型二 用一元一次方程解决工程问题
2.一项工程,估计若由一个人完成需要40天. 现在若2人先做4天,再增加2人和他们一起做,可以完成这项工程. 假设这些人的工作效率相同,那么完成这项工程共用多少天?
题型三 用一元一次方程解决人员调配问题
3.在甲处工作的有272人,在乙处工作的由196人,如果使乙处的人数是甲处工作人数的,应从乙处调多少人到甲处?
随堂训练
一套仪器有一个A部件和三个B部件构成.用1m3钢材可做40个A部件或240个B部件.现要用6m3钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
中考链接
(2012·贵州铜仁)铜仁市对城区主干道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完.设原有树苗x棵,则根据题意列出方程正确的是( )
A. B.
C. D.
数学广角
阿拉伯数字的由来
阿拉伯数字实际是印度人发明的。大约在1500年以前,印度人就已经用一种特殊的字来表示数目,这些字有10个,只要一笔两笔就可以写成。后来,由于各国之间的接触,这些数字传入阿拉伯,阿拉伯人觉得它们很简单,于是在自己的国家开始广泛使用并且把他传到全欧洲。就这样,它们慢慢地就成了我们今天使用的数字。因为阿拉伯人在传播这种数字方面,起的作用很大,人们也就习惯了称这种数字为‘阿拉伯数字
第三章 一元一次方程
3.4 实际问题与一元一次方程(第2课时)
学习目标
1.会根据销售问题中数量关系列方程解决问题,熟练掌握一元一次方程的解法.
2.培养学生数学建模能力,分析问题、解决问题的能力.
3. 通过开放性问题的设计,培养学生创新能力和挑战自我的意识,增强学生的学习兴趣;
自主预习
1. 列一元一次方程解决实际问题的一般步骤包括:
(1)_______;(2)______;(3)_______;
(4)_______;(5)________;(6)_________.
2.解方程:
(1);
(2).
3.销售问题中的等量关系:
(1)售价=标价×__________;
(2)利润率=____________×100%;
(3)利润=______-_______=_______×________.
(利润的两种表示方法是列方程的等量关系)
课堂探究
探究 销售中的盈亏
某商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
分析:
1.如何判断盈利还是亏损?
2.完成下表:
商品 售价/元 进价/元 利润/元 利润率 利润/元
第一件 60 x 盈利25%
第二件 60 y 亏损25%
3.等量关系:
4.列方程解决问题:
归纳:
一般地,当两件商品的售价相同,盈利和亏损率也相同时,总的盈亏情况具有相同的规律吗?
重点题型
题型一 打折销售
1.某商品的售价为每件900元,为了参与市场竞争,商品按售价的9折再让利40元销售,此时仍可获利10%,此商品的进价是多少元?
题型二 销售中的盈亏
2.某商场为减少库存积压,以每件120元的价格出售两件夹克上衣,其中一件盈利20%,另一件亏损20%,在这次买卖中商场是盈利还是亏损,或是不盈不亏?
随堂训练
1.某面粉仓库存放的面粉运出 15%后,还剩余42 500千克,这个仓库原来有多少面粉?
2.小张自主创业开了一家服装店,因为进货时没有进行市场调查,在换季时积压了一批服装.为了缓解资金的压力,小张决定打折出售.若每件服装按标价的5折出售将亏20元,而按标价的8折出售将赚40元.请你算一算每件服装标价多少元?每件服装成本是多少元?
中考链接
(2012·湖南娄底)体育文化用品商店购进篮球和排球共20个,进价和售价如表,全部销售完后共获利润260元.
(1)购进篮球和排球各多少个?
(2)销售6个排球的利润与销售几个篮球的利润相等?
数学广角
一个故事引发的数学家
陈景润一个家喻户晓的数学家,在攻克歌德巴赫猜想方面作出了重大贡献,创立了著名的“陈氏定理”,所以有许多人亲切地称他为“数学王子”。但有谁会想到,他的成就源于一个故事。 1937年,勤奋的陈景润考上了福州英华书院,此时正值抗日战争时期,清华大学航空工程系主任留英博士沈元教授回福建奔丧,不想因战事被滞留家乡。几所大学得知消息,都想邀请沈教授前进去讲学,他谢绝了邀请。由于他是英华的校友,为了报达母校,他来到了这所中学为同学们讲授数学课。 一天,沈元老师在数学课上给大家讲了一故事:“200年前有个法国人发现了一个有趣的现象:6=3+3,8=5+3,10=5+5,12=5+7,28=5+23,100=11+89。每个大于4的偶数都可以表示为两个奇数之和。因为这个结论没有得到证明,所以还是一个猜想。大数学欧拉说过:虽然我不能证明它,但是我确信这个结论是正确的。
第三章 一元一次方程
3.4实际问题与一元一次方程(第3课时)
学习目标
1.在实际问题的探究过程中,弄清问题背景,分析清楚有关数量关系,正确找出列方程所依据的主要相等关系.
2.能根据球赛积分问题中的数量关系,列出一元一次方程,体会方程是刻画现实世界的一个有效的数学模型.
自主预习
1.下表是某年中超联赛中A、B、C、D、E五支球队的积分及胜负情况:
队名 场次 胜场 平场 负场 积分
A 16 8 4 4 28
B 16 0 16 0 16
C 16 0 12 4 12
D 16 5 8 3 a
E 16 b c 2 26
(1)从B队积分可以看出,平一场积 分;
(2)从C队积分可以看出,负一场积 分;
(3)再从A队积分可以看出,胜一场积 分;
(4)观察D、E队提供的信息,可得a= ,
b= ,c= .
2.一次数学小测验共有25道选择题,评分标准如下:答对1题得4分;答错l题扣l分;不答得0 分.已知小明不答的题比答错的题多2道,他的总分是74分,则他答对了多少道题?
课堂探究
探究 球赛积分表问题
下表是某次篮球联赛积分榜:
队名 比赛场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
(1)用式子表示总积分与胜、负场数之间的数量关系;
(2)某队的胜场积分能等于它的负场总积分吗?
分析:
1.表中各队所得积分不同,但各队计算积分的方法是否一样?如果一样,如何计算积分?
2.列式之前要先弄清楚哪几个量?
3.通过观察积分表,选择哪一行的的数据最与众不同?由这一行能看出我们需要的哪个数据?
4.如何计算胜一场积多少分?
5.胜、负一场的积分数都已确定,由于各队胜、负场数各不相同,因此各队积分也不相同,如何在这一个问题中同时表示出这三个变量呢?它们之间是否存在什么不变的关系呢?
重点题型
题型 球赛积分问题
下表是我国2012年中超积分榜情况(截至5月19日).
排名 球队 胜 平 负 积分
1 广州恒大 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 7 1 2 22
2 广州富力 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 7 0 3 21
3 江苏舜天 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 5 3 2 18
4 北京国安 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 5 3 2 18
5 长春亚泰 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 4 3 2 15
6 杭州绿城 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 4 3 4 15
7 贵州人和 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 3 5 2 14
8 天津泰达 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 4 1 5 13
9 大连实德 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 3 3 4 12
10 上海申鑫 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 3 2 6 11
11 辽宁宏运 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 2 5 3 11
12 上海申花 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 2 5 3 11
13 大 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank )连阿尔滨 2 4 4 10
14 河南建业 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 3 1 6 10
15 山东鲁能 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 2 3 4 9
16 青岛中能 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ) 2 2 6 8
根据以上情况,解决下列问题:
(1)足球比赛中胜一场,平一场,负一场各得多少分?
(2)假设广州恒大赛了30场,负了2场,那么它的积分能为45分吗?请说明理由.
随堂训练
1.郑逸同学是学校的篮球明星,在一场篮球比赛中,他一人得了23分,如果他投进的2分球比3分球多4个,那么他一共投进了( )个2分球.
A.3 B.7 C.4 D.8
2.足球比赛的计分规则为:胜一场得3分,平一场得1分,负一场得0分.一支队踢了14场,负5场,共得l9分,那么这支队胜了 ( )
A.3场 B.4场 C.5场 D.6场
3.为了迎接2010年世界杯足球赛的到来,某足球协会举办了一次足球赛,其记分规则及奖励方案(每人)如下表:当比赛进行到每队各比赛l2场时,A队(11名队员)共积20分,并且没有负一场.
(1)试判断A队胜、平各几场;
(2)若每赛一场每名队员均得出场费500元,那么A 队的某一名队员所得奖金与出场费的和是多少元
能力提升
足球比赛的计分规则为:胜一场得3分,平一场得1分,输一场得O分.一支足球队在某个赛季中共需比赛l4场,现已比赛了8场,输了l场,得17分.请问:
(1)前8场比赛中,这支球队共胜了多少场
(2)这支球队打满l4场比赛,最高能得多少分
(3)通过对比赛情况的分析,这支球队打满l4场比赛,得分不低于29分,就可以达到预期目标,请你分析一下,在后面的6场比赛中,这支球队至少要胜几场才能达到预期目标
数学广角
数学家的遗嘱
阿拉伯数学家花拉子密的遗嘱,当时他的妻子正怀着他们的第一胎小孩。“如果我亲爱的妻子帮我生个儿子,我的儿子将继承三分之二的遗产,我的妻子将得三分之一;如果是生女的,我的妻子将继承三分之二的遗产,我的女儿将得三分之一。” 而不幸的是,在孩子出生前,这位数学家就去世了。之后,发生的事更困扰大家,他的妻子帮他生了一对龙凤胎,而问题就发生在他的遗嘱内容。
如何遵照数学家的遗嘱,将遗产分给他的妻子、儿子、女儿呢?
第三章 一元一次方程
3.4实际问题与一元一次方程(第4课时)
学习目标
1.掌握一元一次方程的解法,熟悉用一元一次方程解应用题的基本步骤.
2.经历把实际问题模型化的过程,体会方程思想的作用.
3.通过具体情境引入本节课(电话计费问题),使学生感受数学的魅力和作用.
自主预习
为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.
该市自来水收费价格见价目表:
价 目 表
每月用水 单 价
不超出6m3的部分 2元/ m3
超出6m3不超出10m3的部分 4元/ m3
超出10m3的部分 8元/ m3
(1)若某户居民1月份用水8m3,则应收水费:
____________元;
(2)若某户居民2月份用水12.5m3,则应收水费________元;
(3)若某户居民3、4月份共用水15m3(4月份用水量超过3月份),共交水费44元,则该户居民3、4月份各用水多少m3?
课堂探究
电话计费问题
下表中有两种移动电话计费方式
考虑下列问题:
(1) 设一个月内用移动电话主叫为t min(t是正整数),根据上表说明:当t在不同时间范围内取值时,按方式一和方式二如何计费.
(2) 你能从中发现如何根据主叫时间选择省钱的计费方式吗?
1.你能解读方式一中是如何计费的吗?方式二呢?
2.在方式一中,计费与什么有关?方式二中呢?
3.小明一个月主叫时间100 min,按方式一和方式二计费,哪个计费少?200 min呢?300 min 呢?是否存在一个时间t,两种方式计费一样多呢?你能列出方程吗?
重点题型
题型 纳税问题
2005年10月27日全国人大通过《关于修改<中华人民共和国个人所得税>的决定》,征收个人所
得税的起点从800元提高到1 600元,也就是说,原来月收入超过800元的部分为全月应纳税所得额,从2006年1月1日起,月收入超过1 600元的部分为全月应纳税所得额. 税法修改前后全月应纳税所得额的划分及相应的税率相同,见下表:
全月应纳税所得额 税率(%)
不超过500元的部分 5
超过500至2 000元的部分 10
超过2 000至5 000元的部分 15
… …
某人2005年12月依法缴纳本月个人所得税115元,假如本月按新税法计算,此人应少纳税多少元?
随堂训练
1.中国移动某分公司开设适合普通用户的两种通讯业务,分别是:
“龙城通”用户先缴25元月租,然后每分钟通话费用0.2元;“神州行”用户不用缴纳月租费,每分钟通话费用0.4元. (通话均指拨打本地电话)
(1)一个月内通话多少分钟,两种移动通讯方式费用相同?
(2)若李老师一个月通话约80分钟,请你给他提个建议,应选择哪种移动通讯方式合算一些?请说明理由.
中考链接
(2012 天津中考)某通讯公司推出了移动电话的两种计费方式(详情见下表).
温馨提示:若选方式一,每月固定缴费58元,当主动打出的电话月累计不超过150分,不再额外缴费;当超过150分,超过部分每分钟加收0.25元.
设一个月内使用移动电话主叫的时间为t分(t为正整数),请根据表中提供的信息回答下列问题:
(1)用含有t的式子填写下表:
(2)当t为何值时,两种计费方式的费用相等?
(3)当330<t<360时,你认为选用哪种计费方式省钱(直接写出结果即可)
这批书的总数有几种表示法?它们之间有什么关系?
