人教版七年级上册第4章图形的初步全章学案18页
文档属性
| 名称 | 人教版七年级上册第4章图形的初步全章学案18页 |
|
|
| 格式 | zip | ||
| 文件大小 | 563.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-22 00:00:00 | ||
图片预览

文档简介
第四章 几何图形初步
4.1.1 立体图形与平面图形 (第1课时)
学习目标
1.通过观察生活中的大量图片或实物,体验、感受、认识生活中的事物为原型的几何图形,认识一些简单几何体的基本特性,能识别这些几何体.
2.能由事物形状想象出几何图形,由几何图形想象出事物形状,进一步丰富对几何图形的感性认识.
自主预习
观察图形: (1) 粉笔盒 (2) 茶叶桶 (3) 足球 (4) 交通标志.回答下列问题:
(1) (2) (3) (4)
(1) 请从中找出我们熟悉的几何图形,归纳一下我们常见的几何图形有哪些?
(2) 你能把(1)题中的几何图形按立体图形与平面图形分类吗?生活中还有哪些物体的形状类似于这些几何图形?
课堂探究
探究一 几何图形
1.观察纸盒外形并填空:
从整体上看,它的形状是______ ;看不同的侧面,得到的是______或______ ;看棱得到的是 ______ ;看顶点得到的是______
2.研究几何图形的内容是什么?
探究二 立体图形
1.举例说明什么是立体图形.
2.下图中的实物形状对应哪些立体图形?把相应的实物与图形用线连起来.
归纳:
常见的立体图形,并指出各部分的名称及特征.
柱体: (2)椎体:
(3)台体: (4)球体
探究三 平面图形
举例说明什么是平面图形.
归纳:常见的平面图形:
(1)点; (2)线:直线、射线、线段;
(3)三角形 (4)四边形:正方形、长方形、平行四边形、梯形 (5)圆、扇形
重点题型
题型 立体图形的识别
1.下列判断正确的有 ( )
①正方体是棱柱,长方体不是棱柱;②正方体是棱柱,长方体也是棱柱;③正方体是柱体,圆柱也是柱体;④正方体不是柱体,圆柱是柱体.
A.1个 B.2个 C.3个 D.4个
2.写出下列立体图形的名称:
随堂训练
1.对于一个物体,数学中关注的是 ( )
A.材料,颜色 B.做工,美观
C.形状,大小 D.质量,价值
2.棱柱的侧面都是 ( )
A.三角形 B.长方形 C.五边形 D.菱形
3.圆锥的侧面展开图是 ( )
A.长方形 B.正方形 C.圆 D.扇形
4.请在下图所示的图形下面的横线上写出它们的名称.
_______ _______ _______ _______
5.下面几种图形: ①三角形;②长方形;③正方体;④圆;⑤圆锥;⑥圆柱。其中属于立体图形的是________________.(填上序号即可)
6.下列图形中主要是由哪些简单的图形组成的?
能力提升
1.先将下列几何图形分为两类,再对每一类进行分类,并说明你分类的理由.
2.请用直线、线段、三角形、圆这几种图形设计成表现客观事物的图画,并为你的图画命名.(每幅图可以用一种、两种或三种基本图形,但总数不得超过三个).
数学广角
“欧氏几何”…几何学的一门分科。公元前3世纪,古希腊数学家欧几里德把人们公认的一些几何知识作为定义和公理,在此基础上研究图形的性质,推导出一系列定理,组成演绎体系,写出《几何原本》,形成了欧氏几何。在其公理体系中,最重要的是平行公理,由于对这一公理的不同认识,导致非欧几何的产生。按所讨论的图形在平面上或空间中,分别称为“平面几何”与“立体几何”。
欧几里德几何指按照欧几里德的《几何原本》构造的几何学。
欧几里德几何有时就指平面上的几何,即平面几何。三维空间的欧几里德几何通常叫做立体几何。 高维的情形请参看欧几里德空间。
数学上,欧几里德几何是平面和三维空间中常见的几何,基于点线面假设。数学家也用这一术语表示具有相似性质的高维几何。
第四章 几何图形初步
4.1.1立体图形与平面图形 (第2课时)
学习目标
1.能画出从不同方向看一些基本几何体以及它们
的简单组合得到的平面图形.
2.直观认识立体图形和展开图,了解研究立体图形的方法.
3.通过观察和动手操作,经历和体验平面图形和立
体图形相互转化的过程,初步建立空间观念,发
展几何直观.
自主预习
我们从不同的角度、不同的方向去观察同一物体
时,看到的图像一定一样吗?请举出生活中从不
同方向观察同一对象的实例.你能用一首诗句描
述这种现象吗?
准备一个包装盒(形状不限),沿着边剪开、铺
平, 看看它的展开图是由哪些平面图形组成的,再把展开的纸板复原,你有什么体会?
课堂探究
探究一 从不同的方向看物体
1.从不同的方向看物体是指从哪些方向?
2.下图是一个由9个正方体组成的立体图形,分别从正面、左面、上面观察这个图形,各能得到什么平面图形?你能画出来吗?
归纳:
几种常见几何体,分别从正面、左面、上面看到的平面图形:
探究二 立体图形的展开图
1.下面的图形是一些立体图形的展开图,用它们能围成什么样的立体图形?把它们画在一张硬纸片上,剪下来,折叠、粘贴,看看得到的图形和你想象的是否一样?
2.画出正方体的展开图.
归纳:
不是所有的立体图形都有展开图,如球;
由立体图形的展开图可识别出立体图形的形状,具体方法是:展开图中有圆,一般考虑圆柱或圆锥;展开图中有三角形,一般考虑棱柱或棱锥;展开图中有长方形或正方形,一般考虑棱柱;
正方体的展开图:
重点题型
题型一 从不同方向看集合体
1.桌上放着一个球和一个圆柱,下面a、b、c、d、e这五幅图分别是从什么方向看到的?题型二 简单几何体的展开图
2.一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面是( )
A.和 B.谐
C.沂 D.南
随堂训练
一个几何体从正面看、左面看、上面看都是正
方形,则这个立体图形是 .
2.从不同方向看到的一立体图形如图所示,那么
这个立体图形是 .
3.一个正方体中,截去一个小正方体的立体图如图所示,从左面观察这个图形,得到的平面图形是 ( )
4.如图所示的物体,从左面看得到的图是( )
A B C D
5.下面形状的四张纸板,按图中线经过折叠可以
围成一下直三棱柱的是 ( )
A B C D
6.下图中不是正方体的表面展开图的是 ( )
A B C D
7.分别从正面、左面、上面观察三棱柱和四棱锥,
看一看各能得到什么平面图形
能力提升
1.下面是一些立体图形的展开图,用它们能围 成什么样的立体图形?
2.正方体展开图如下,原正方体相对两个面上的数字之和的最小值的是 .
数学广角
动物中的数学“天才”
蜜蜂蜂房是严格的六角柱状体,它的一端是平整的六角形开口,另一端是封闭的六角菱锥形的底,由三个相同的菱形组成,组成底盘的菱形的钝角为109度28分,所有的锐角为70度32分,这样既坚固又省料,蜂房的巢壁厚0.073毫米,误差极少。
第四章 几何图形初步
4.1.2 点、线、面、体
学习目标
1.通过丰富的实例,进一步认识点、线、面、体的几何特征,感受它们之间的关系.
2.培养操作、观察、分析、猜测和概括等能力,同时渗透转化、化归、变换的思想.
自主预习
1.观察你使用的数学课本,它有几个面?面与面相交的地方形成了几条线?线与线相交成几个点?总结点、线、面、体的关系,并举出生活中另外一些实例说明这一关系.
2.找出生活中包含平面、曲面、直线、曲线、点的例子.
注意:
点、线、面是够成几何图像的基本元素,几何中点无大小(点是位置的标志),线无粗细,面无厚薄.
课堂探究
探究一 点、线、面、体
1.几何图形是由什么组成的?什么是构成图形的基本元素?
2.观察图形填空:
这是一个长方体模型,围成它的有 个面, 面与面相交的地方形成了 条线,线与线相交成 个点.
这是一个圆柱模型,围成它的有 个面, 面与面相交的地方形成了 条线.与长方体有 何不同?
归纳:
体是 围成的,面有 也有 ;面与面相交形成 ,线有 也有 ;线与线相交形成 ,点没有 ___________之分.
3.笔尖可以看作一个点,这个点在纸上运动时,形成了什么图形?想一想,从中你又有何发现?请用最简练的语言概括你的发现.
4.汽车雨刷可以看作一条线,它在挡风玻璃上来回摆动时有什么现象?
5.点动成线,线动成面.那么请同学们想一想,当面运动时会形成什么图形?如何验证你的猜想?
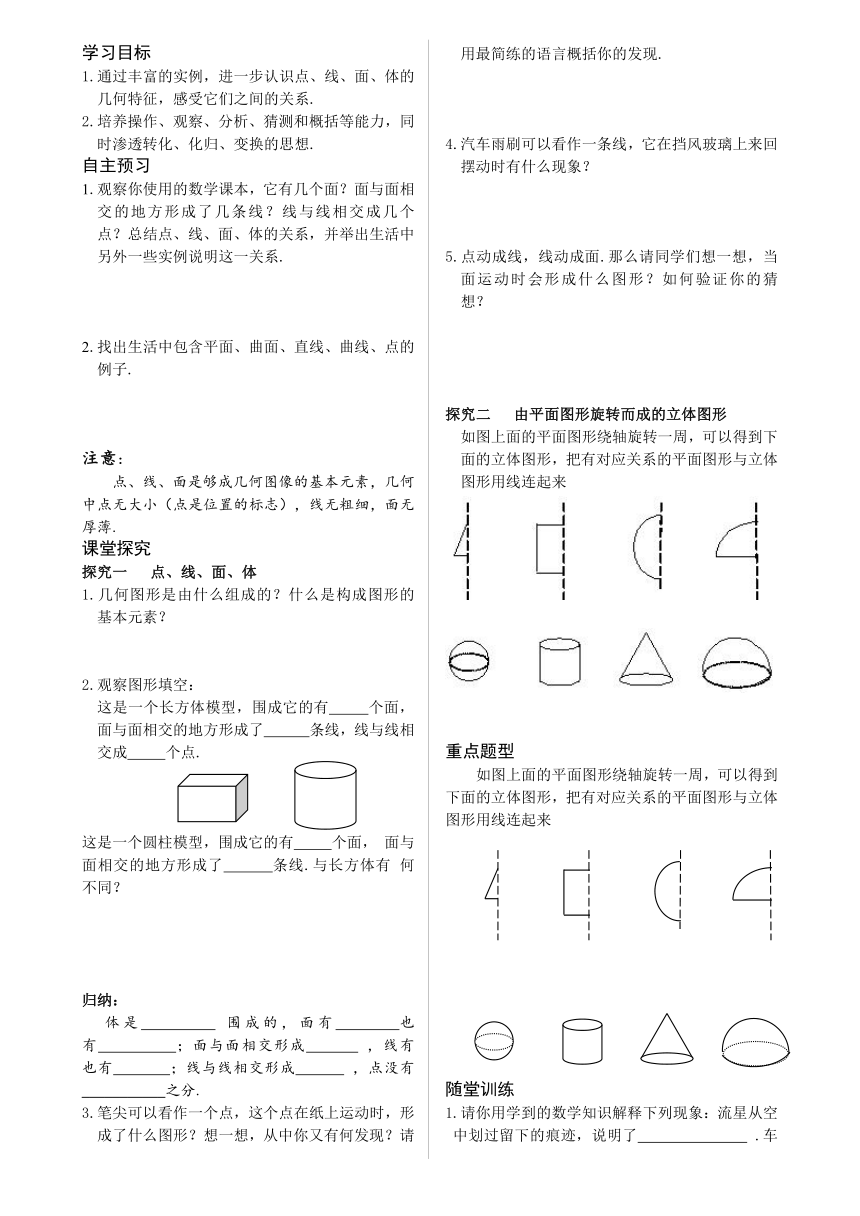
探究二 由平面图形旋转而成的立体图形
如图上面的平面图形绕轴旋转一周,可以得到下面的立体图形,把有对应关系的平面图形与立体图形用线连起来
重点题型
如图上面的平面图形绕轴旋转一周,可以得到下面的立体图形,把有对应关系的平面图形与立体图形用线连起来
随堂训练
1.请你用学到的数学知识解释下列现象:流星从空中划过留下的痕迹,说明了 .车轮转动时,看起来像一个整体的圆面,这说明了 .一枚硬币在光滑的桌面上快速旋转形成一个球,这说明了
2.如图所示的几何体由 个面围成,面与
面相交有 条线,直的线有 条,曲的
线有 _______条.
3.四棱锥有 个面,面与面相交形成了 ________条棱,这些棱相交形成了 个点.
4.将长方形按图中所示的四种方法旋转,能得到圆柱体是 _____.
5.如图,用第一行的图形绕轴旋转一周,便能形成第二行的某个几何体,请你用线连一连.
6.如图所示,要给这个长,宽,高分别为xcm,ycm,zcm的箱子打包,其打包方式如图所示,则打包带的长至少要多少?(用含x,y,z的代数式表示)
能力提升
现有一个长为8cm,宽为6cm的长方形,分别绕它的长、宽所在直线旋转一周,得到不同的圆柱体,它们的体积分别是多少?(结果用π表示).
数学广角
谜语“千条线万条线,落在水里看不见”,你能用数学知识解释这一现象吗?
第四章 几何图形初步
4.2直线、射线、线段(第1课时)
学习目标
1.认识直线、射线、线段的区别与联系,逐步掌握他们的表示方法.
2.结合实例,了解两点确定一条直线的基本事实,并逐步应用.
3.能根据语句画出相应的图形,会用语句描述简单的图形,在图形的基础上发展数学语言.
自主预习
1.硬纸条固定在硬板上至少需要几颗图钉?若将图钉抽象为点,纸条抽象成直线,你能得到什么结论?请画图说明.
2.如何表示直线、射线、线段.
3.怎样由图中的线段得到一条射线或一条直线.
课堂探究
探究一 直线公理
1.经过一点能画几条直线?经过两点能画几条直线?如下图画一画试一试.
归纳:
经过一点可以画____条直线;经过两点有___直线,并且_____直线(即两点确定一条直线).
探究二 直线、射线、线段的定义及表示
1.如图,直线有几种表示方法?如何表示?
2.如图,射线有几种表示方法?如何表示?
3.如图,线段有几种表示方法?如何表示?
4.在直线、射线、线段的表示法中,为什吗用两个大写字母表示?
归纳:
名称 不同点 联 系
图形 延伸方向 端点个数 度量
直线
射线
线段
5.用几何语言描述下列图形.
归纳:
点与直线有什么位置关系?
重点题型
题型一 按要求画图
1.如图平面上有四点A、B、C、D,按下列语句画图:
如图平面上有四点A、B、C、D (1)画直线AB、射线BC与线段DC;
(2)延长CD与直线AB相交于点E;
(3)画线段AC、BD交于点F;
(4)连接AD,并使其反向延长与射线CB交于点G.
题型二 射线、线段的条数的确定
2.根据图形,确定直线上射线和线段的条数,并归纳结论.
随堂训练
1.点与直线的位置关系有两种,分别是_________和__________.
2.用枪瞄准射击时,总是用一只眼对准准星和目标,用数学知识解释为 _______________.
3.下列说法:①直线的一半是射线;②射线AB和射线BA是同一条射线;③线段AB与线段BA是同一条线段;④直线AB和直线BA是同一条直线;⑤一条直线上一点把这条直线分成两条射线,其中正确的是________(填上序号即可).
4.下列写法中正确的是 ( )
A.直线a、b相交于点n
B.直线AB、CD相交于点M
C.直线ab、cd相交于点M
D.直线AB、CD相交于m
5.如图,在直线上依次有五个点A、B、C、D、E,则图中射线的条数为 ( )
A.2条 B.10条 C.5条 D.4条
6.如图,点A、B、C是直线m上的三个点,图中共有线段的条数是 ( )
A.1条 B.2条 C.3条 D.4条
7.下列语句正确的是 ( )
A.画直线AB=10厘米
B.延长射线OA
C.画射线OB=3厘米
D.延长线段AB到点C,使BC=AB
8.在直线m上有A、B、C三点,下列说法正确的有 ( )
①射线AB与射线BC是同一条射线;②直线AB经过点C;③射线AB与射线AC是同一条射线;④直线AB与直线BC是同一条直线.
A.1个 B.2个 C.3个 D.4个
能力提升
平面上有三点A、B、C,过其中每两点画直线,一共可画几条?四点呢?n个点呢?试画图说明.
数学广角
几何发展史
几何, 是由希腊文演变而来,其原意是土地测量。是埃及人创造的,并且产生于土地测量。由于尼罗河泛滥,经常冲毁界限,这样测量变成了必要的工作。无可置疑的,这类科学和其它科学一样,都发生于人类的需要。”明代徐光启(1562~1633)和天主教耶酥会传教士利玛窦翻译欧几里得的《几何原本》时将Geometry一词译为几何学。
第四章 几何图形初步
4.2直线、射线、线段(第2课时)
学习目标
1.会画一条线段等于已知线段.
2.结合图形认识线段间的数量关系,学会比较线段的大小,理解线段的和、差以及线段中点的意义.
3.理解两点间距离的意义,能度量两点间的距离.
自主预习
1.任意画线段,怎样再画一条与线段长度相等的线段
2.阅读课本,利用下图中的已知线段,分别画线段,线段,并谈谈你对线段的中点、三等分点、四等分点的认识.
课堂探究
探究一 线段的比较与和差
1.已知一条线段a,怎样画一条线段AB,使AB=a,动手画一画.
2.有两条线段,你能判断一下它们的长短吗?你有什么方法来验证你的判断?
归纳:
比较两条线段的方法:
3.已知线段a和b(a>b),怎样画一条线段AC=a+b 怎样画一条线段AD=a-b?动手画一画.
探究二 线段的中点、三等分点
1.什么是线段的中点?
2.线段的中点具有什么性质?
3.若AM=BM,则M是AB的中点吗?若AM=AB,BM=AB,则点M是AB的中点吗?
4.什么是线段的三等分点?具有什么性质?
探究三 线段的性质及两点的距离
1.如图,从A地到B地有四条道路,除它们之外能否再修一条从A地到B地的最短道路?
如果能,请联系你以前所学的知识,在图上画出最短线路.
归纳:
由问题1,你能得到什么结论?
2.什么叫两点的距离?
重点题型
题型一 线段间的数量关系及计算
1.如图所示,为线段的中点,为线段的中点,,求的长.
题型二 两点间距离
2.若点在线段上,=8cm,=5cm,,则,两点间的距离是( )
A.3cm B.13cm
C.3cm或13cm D.不确定
随堂训练
1.估计下列图形中、AC的大小关系,再用刻度尺或圆规检验你的估计.
2. 如图所示,已知线段,, 画一条线段,使它等于.
3.如图所示,点C是AB的中点,点D是BC的
点,则下列表达式:① ;②;③;④,其中正确的是______.(填上序号)
4.如图所示,已知,是的中点,,求,, 长.
能力提升
如图,线段,点是线段上一点,,分别是线段,的中点,小华据此轻松地求得.他在反思过程中突发奇想:若点运动到的延长线上,原有的结论“”是否依然成立?请帮小华画出图形并说明理由.
数学广角
蜗牛何时爬上井?
一只蜗牛不小心掉进了一口10米深的枯井里,它决心爬出去。它不停的爬呀,到了傍晚终于爬了5米。心想:“照这样的速度,明天傍晚我就能爬上去。”想着想着,它不知不觉地睡着了。早上,蜗牛发现睡着以后从井壁上滑下来4米。蜗牛叹了一口气,咬紧牙又开始往上爬。到了傍晚又往上爬了5米,可是晚上蜗牛又滑下4米。爬呀爬,最后坚强地蜗牛终于爬上了井台。小朋友你能猜出来,蜗牛需要
用几天时间就能爬上井台吗?
第四章 几何图形初步
4.3.1 角
学习目标
1.理解角的定义和相关概念,用运动的观点理解角、平角、周角等概念,掌握角的表示方法.
2.掌握角的度量及度量单位之间的转化.
自主预习
1.请举出几个生活中给我们角的形象的物体,根据你对角的理解,画出几个不同形状的角并指出角的两边是什么图形
2.指出图中的角的顶点和边,并用三种方法表示该角.
3.度、分、秒是常用的角的度量单位,它们之间的互化方法与时间单位间的互化方法类似,请你完成下列各题.
(1)1.45°等于多少分 等于多少秒
(2)900″等于多少分 等于多少度
课堂探究
探究一 角的概念和表示
1.有 的两条 组成的图形叫做角. ___ ____叫角的顶点,
叫角的边.
2.下面三个角各可以如何表示?写在对应角的下面.
3.角也可以看作由 绕着它的 旋转而形成的图形.如图,射线绕点旋转,当终止位置和起始位置 时,
形成的角是平角;继续旋转,和重合时,形成的角是 .
归纳:
(1)用三个大写字母表示角时,顶点字母必须写在 _____ .(2) 用一个大写字母表示角时,必须顶点处只有 个角.(3)用数字或希腊字母表示角时,必须在相应角的内部加弧线及数字(或希腊字母).
探究二 角的度量及转换
1.度、分、秒是常用的角的度量单位.把一个周角360等分,每一份就是 的角,记作;把1度的角60等分,每一份叫做1分的角,记作 ;把1分的角60等分,每一份就是1秒的角, 记作 .
2.1周角= °,1平角= °,
1°= ′, 1′= ″.
的度数是49度20分24秒,记作= .
3.()°= ′= ″;
5760″= ′= °.
归纳:
度、分、秒的转化是___进制,由度化分,由分化秒,需乘以___;由秒化分,由分化度,只要除以___即可.
重点题型
题型 角的表示
1.写出图中:
(1)能用一个字母表示的角;
(2)以B为顶点的角;
(3)图中共有几个角?
2.以点O为端点引4条射线,此时图中共有多少个角?怎样表示?
题型二 度、分、秒之间的换算
1.0.75°= ′= ″,
34.37°= ° ′ ″.
2.1 800″= °,39°36′= °
随堂训练
1.若∠α=30°18′,∠β=30.18°,∠γ=30.3°,则下列结论正确的是 ( )
A.∠α=∠β B.∠α=∠γ
C.∠β=∠γ D.∠α、∠β、∠γ互不相等
2.在钟表上,8时整,时针与分针所成的角是 ;l时30分时,时针与分针所成的角是 .
3.根据下列语句画图:
(1)画∠AOB=80°; (2)在∠AOB的内部画射线OC,使∠BOC=60°; (3)在∠AOB的外部画射线OD,使∠DOA=30°.
4.角的运算
(1)23°31′25″+42°27′56″;
(2)42°31′56″-23°37′;
(3)23°31′25″×3.
能力提升
如图以O为端点的射线共4条,其中任一条射线与其他3条射线都必构成一个角(小于平角的角),这样,可得4×3个角,但这些角中,每一个角都重复了一次,所以4条射线共组成角的个数为=6.
同理,如果从O点引5条射线(每两条射线不在同一直线上),那么以这个点为顶点的角的个数为 个;
如果从O点引n条射线(每两条射线不在同一直线上),那么以这个点为顶点的角的个数为 多少个?你能解释其中的道理吗
数学广角
动物中的数学“天才”
蜜蜂蜂房是严格的六角柱状体,它的一端是平整的六角形开口,另一端是封闭的六角菱锥形的底,由三个相同的菱形组成。组成底盘的菱形的钝角为109度28分,所有的锐角为70度32分,这样既坚固又省料。蜂房的巢壁厚0.073毫米,误差极小。
丹顶鹤总是成群结队迁飞,而且排成“人”字形。“人”字形的角度是110度。更精确地计算还表明“人”字形夹角的一半——即每边与鹤群前进方向的夹角为54度44分8秒!而金刚石结晶体的角度正好也是54度44分8秒!是巧合还是某种大自然的“默契”?
蜘蛛结的“八卦”形网,是既复杂又美丽的八角形几何图案,人们即使用直尺的圆规也很难画出像蜘蛛网那样匀称的图案。
第四章 几何图形初步
4.3.2 角的比较与运算
学习目标
1.会比较角的大小,理解两个角的和、差的意义.
2.掌握角平分线的概念;能够利用角平分线的定义来解决相关的计算问题.
自主预习
1.如何比较两条线段的大小 那么,你能比较两个角的大小吗 如图,已知∠ABC和∠DEF,试一试.
2.如图,回答下列问题:
(1)图中有多少个角 请你表示出这些角之间的关系;
(2)若∠AOB=120°,∠AOC=26°8′,求∠BOC的度数.
3.在透明纸上画一个∠AOB,如图,沿着顶点对折,使角的两边重合,折痕为0C,回答下列问题:
(1)用式子表示出∠AOB、∠AOC和∠BOC的数量关系;
(2)射线OC叫做什么
(3)若∠AOB=45°3′,求∠AOC的度数.(精确到分)
课堂探究
探究一 分类讨论解决角的和差问题
1.已知∠AOB =80°,∠AOC=40°,求∠BOC的度数.
问题1:按照题意画出图形;
问题2:∠AOB与∠AOC有怎样的位置关系;
问题3:∠AOB 、∠AOC和∠BOC之间有怎样的数量关系?
探究二 角平分线及性质
1.结合图形,说明什么是角平分线?
2.OC是∠AOB的角平分线,∠AOC、∠BOC与∠AOB之间有什么关系?
3.若∠AOC=∠BOC,则OC是角平分线吗?若∠AOC=∠AOB,则OC是角平分线吗?
4.什么是角的三等分线?按下图说明.
重点题型
题型一 角的和差
1.已知∠AOB=120°,∠BOC=30°,求∠AOC的度数.
题型二 角平分线
2.如图所示,OC是∠AOB平分线, 0D 平分∠AOC,且∠AOB=98°,
则∠COD为 ( )
A.24°30′ B.24°5 ′
C.2° D.30°
3.已知:如图,∠AOB=130°,OE平分∠BOC,OF平分∠AOC.求∠EOF的度数.
随堂训练
1.下列说法正确的是 ( )
A.两条射线就是一个周角
B.一条射线就是一个周角
C.角的两边越长,角就越大
D.一条射线绕着端点从起始位置旋转到终止位置所形成的图形叫做角
2.用放大5倍的放大镜看l0°的角,观察到的角的度数为 ( )
A.10° B.50° C.2° D.以上都不对
3.小亮利用星期天进行社会调查活动,早晨8:00出发, 中午12:30到家,问小亮到家时时针和分针的夹角为 ( )
A.85° B.150° C.180° D.165°
4.点D在∠AOB的内部,下列等式不能表示0D是角平分线的等式是 ( )
A.∠AOD=∠BOD B.∠AOD=∠BOD
C.∠AOD=∠AOB D.∠AOB=2∠BOD
5.计算:
(1)20°17′×6; (2)156°33′÷5.
6.用三角板画出105°,l35°的角.
能力提升
如图所示,0是直线AC上一点,0B是一条射线,OD平分∠AOB,0E在∠BOC内,∠BOE=∠E0C,∠DOE=70°,求∠EOC.
中考链接
1.(2012·广州)已知∠ABC=30°,BD是∠ABC的平分线,则∠ABD=________度.
2.(2012·北京)如图,直线,交于点,射线平分,若,则等于( )
A. B. C. D.
数学广角
1832年5月30日晨,在巴黎的葛拉塞尔湖附近躺着一个昏迷的年轻人,过路的农民从枪伤判断他是决斗后受了重伤,就把这个不知名的青年抬到医院。第二天早晨十点钟,他就离开了人世。数学史上最年轻、最有创造性的头脑停止了思考。人们说,他的死使数学发展推迟了好几十年。这个青年就是死时不满21岁的伽罗华。
第四章 几何图形初步
4.3.3 余角和补角
学习目标
1.认识一个角的余角和补角.
2.掌握余角和补角的性质.
3.了解方位角,能确定具体物体的方位,进一步渗透数形结合的思想.
自主预习
1.如果两个角的和是__________,那么这两个角叫做互为余角,其中一个角是另一个角的_____.
2.如果两个角的和是__________,那么这两个角叫做互为补角,其中一个角是另一个角的_____.
3.填下列表:
∠a ∠a的余角 ∠a的补角
45°
77°
62°2′
x°
结论:同一个锐角的补角比它的余角大_______.
4.和都是的补角,则__.
5.如果,则的关系 ,理由是 .
6.在点O 北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,则∠AOB的度数是( ) A. 100° B. 70° C. 180° D. 140°
课堂探究
探究一 余角和补角的定义及性质
1.画一个直角∠AOB和一个平角∠CPD,分别过两个角的顶点画射线ON、PM.
2.射线将直角和平角分成几部分?它们的度数关系如何?
3.将两个角拉开,它们的度数关系有变化吗?这说明什么问题?
归纳:
互为余角、互为补角的概念.
4.如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
归纳:
余角的性质:
5.如图, ∠1与∠2互补,∠3与∠4互补, ∠2= ∠3,那么∠1与∠4相等吗?为什么?
归纳:
补角的性质:
探究二 方位角
1.什么是方位角?
2.平面图形上的方向是怎么规定的?
3.在方位角的表示中把什么方向写在前,把什么方向写在后?
4.如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
重点题型
题型一 余角和补角的概念
1.若一个角的补角等于它的余角4倍,求这个角的度数.
题型二 余角和补角的性质
2.点 A、O、B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠COB,图中哪些角互为余角?
题型三 方位角应用
3.从A看B的方向是北偏东21°,那么B看A的方
向是( )
A.南偏东69° B.南偏西69°
C.南偏东21° D.南偏西21°
随堂训练
1.52°24′的余角是_______,补角是________.
2.射线OA方向是东北方向,射线OB方向是北偏西60°,则∠AOB度数是______.
3.己知∠α与∠β互余,且∠α=150 ,则∠β的补角为 度.
4.下列正确的有 ( )
⑴一个角的补角一定是钝角;⑵互补的两个角不可能相等;⑶若∠A+∠B+∠C=90 ,则∠A+∠B是∠C的余角;⑷∠A的补角与∠A的余角的差一定等于直角;⑸两个锐角一定互为余角;⑹直角没有补角,⑺如果∠MON=180 ,那么M、O、N三点在一条直线上.
A.1个 B.2个 C.3个 D.4个
5. 和北偏西40°的射线OA组成平角AOB的射线OB是 ( )
A.南偏东40°的射线 B.南偏东50°的射线
C.南偏东60°的射线 D.东南方向的射线
6.已知有一条射线OA,若从点O再引两条射线OB、OC,且∠AOB=72°,∠BOC=36°,则∠AOC的度数是 ( )
A.36° B.108° C.72°或36° D.36°或108°
7.如图,∠AOC=∠COB=90°,∠DOE=90°,A、O、B三点在一直线上
(1)写出∠COE的余角,∠AOE的补角;
(2)找出图中一对相等的角,并说明理由 .
能力提升
已知:如下图,点A、O、B在同一直线上,∠1与∠2互余,OE、OF分别是∠AOC、∠AOD的平分线,求∠EOF的度数.
中考链接
1.(2012·江苏泰州)已知∠α的补角是130°,则∠α= 度.
2.(2012·江西)如图 所示,如果在阳光下你的身影的方向北偏东60°方向,那么太阳相对于你的方向是( )
A. 南偏西60° B.南偏西30°
C.北偏东60° D.北偏东30°
数学广角
牛顿是举世公认的、有史以来最伟大的科学家之一。23毕业于著名的剑桥大学后留校工作。后因逃避伦敦流行的鼠疫来到母亲的农场里。在这里,他被一个常人熟视无睹的现象吸引住了。有一次,他看到一个熟透了的苹果落在地上,便开始思索为什么苹果会垂直落在地上,而不是飞到天上去呢?一定是有一种力在拉它,那么这种将苹果往下拉的力会不会控制月球?他就是通过这个看起来十分简单的现象,发现了著名的万有引力
●
建
设
和
谐
沂
南
z
x
y
A
B
a
b
A
B
(1)
(2)
(3)
A
B
C
A
A
B
B
C
C
a
b
4.1.1 立体图形与平面图形 (第1课时)
学习目标
1.通过观察生活中的大量图片或实物,体验、感受、认识生活中的事物为原型的几何图形,认识一些简单几何体的基本特性,能识别这些几何体.
2.能由事物形状想象出几何图形,由几何图形想象出事物形状,进一步丰富对几何图形的感性认识.
自主预习
观察图形: (1) 粉笔盒 (2) 茶叶桶 (3) 足球 (4) 交通标志.回答下列问题:
(1) (2) (3) (4)
(1) 请从中找出我们熟悉的几何图形,归纳一下我们常见的几何图形有哪些?
(2) 你能把(1)题中的几何图形按立体图形与平面图形分类吗?生活中还有哪些物体的形状类似于这些几何图形?
课堂探究
探究一 几何图形
1.观察纸盒外形并填空:
从整体上看,它的形状是______ ;看不同的侧面,得到的是______或______ ;看棱得到的是 ______ ;看顶点得到的是______
2.研究几何图形的内容是什么?
探究二 立体图形
1.举例说明什么是立体图形.
2.下图中的实物形状对应哪些立体图形?把相应的实物与图形用线连起来.
归纳:
常见的立体图形,并指出各部分的名称及特征.
柱体: (2)椎体:
(3)台体: (4)球体
探究三 平面图形
举例说明什么是平面图形.
归纳:常见的平面图形:
(1)点; (2)线:直线、射线、线段;
(3)三角形 (4)四边形:正方形、长方形、平行四边形、梯形 (5)圆、扇形
重点题型
题型 立体图形的识别
1.下列判断正确的有 ( )
①正方体是棱柱,长方体不是棱柱;②正方体是棱柱,长方体也是棱柱;③正方体是柱体,圆柱也是柱体;④正方体不是柱体,圆柱是柱体.
A.1个 B.2个 C.3个 D.4个
2.写出下列立体图形的名称:
随堂训练
1.对于一个物体,数学中关注的是 ( )
A.材料,颜色 B.做工,美观
C.形状,大小 D.质量,价值
2.棱柱的侧面都是 ( )
A.三角形 B.长方形 C.五边形 D.菱形
3.圆锥的侧面展开图是 ( )
A.长方形 B.正方形 C.圆 D.扇形
4.请在下图所示的图形下面的横线上写出它们的名称.
_______ _______ _______ _______
5.下面几种图形: ①三角形;②长方形;③正方体;④圆;⑤圆锥;⑥圆柱。其中属于立体图形的是________________.(填上序号即可)
6.下列图形中主要是由哪些简单的图形组成的?
能力提升
1.先将下列几何图形分为两类,再对每一类进行分类,并说明你分类的理由.
2.请用直线、线段、三角形、圆这几种图形设计成表现客观事物的图画,并为你的图画命名.(每幅图可以用一种、两种或三种基本图形,但总数不得超过三个).
数学广角
“欧氏几何”…几何学的一门分科。公元前3世纪,古希腊数学家欧几里德把人们公认的一些几何知识作为定义和公理,在此基础上研究图形的性质,推导出一系列定理,组成演绎体系,写出《几何原本》,形成了欧氏几何。在其公理体系中,最重要的是平行公理,由于对这一公理的不同认识,导致非欧几何的产生。按所讨论的图形在平面上或空间中,分别称为“平面几何”与“立体几何”。
欧几里德几何指按照欧几里德的《几何原本》构造的几何学。
欧几里德几何有时就指平面上的几何,即平面几何。三维空间的欧几里德几何通常叫做立体几何。 高维的情形请参看欧几里德空间。
数学上,欧几里德几何是平面和三维空间中常见的几何,基于点线面假设。数学家也用这一术语表示具有相似性质的高维几何。
第四章 几何图形初步
4.1.1立体图形与平面图形 (第2课时)
学习目标
1.能画出从不同方向看一些基本几何体以及它们
的简单组合得到的平面图形.
2.直观认识立体图形和展开图,了解研究立体图形的方法.
3.通过观察和动手操作,经历和体验平面图形和立
体图形相互转化的过程,初步建立空间观念,发
展几何直观.
自主预习
我们从不同的角度、不同的方向去观察同一物体
时,看到的图像一定一样吗?请举出生活中从不
同方向观察同一对象的实例.你能用一首诗句描
述这种现象吗?
准备一个包装盒(形状不限),沿着边剪开、铺
平, 看看它的展开图是由哪些平面图形组成的,再把展开的纸板复原,你有什么体会?
课堂探究
探究一 从不同的方向看物体
1.从不同的方向看物体是指从哪些方向?
2.下图是一个由9个正方体组成的立体图形,分别从正面、左面、上面观察这个图形,各能得到什么平面图形?你能画出来吗?
归纳:
几种常见几何体,分别从正面、左面、上面看到的平面图形:
探究二 立体图形的展开图
1.下面的图形是一些立体图形的展开图,用它们能围成什么样的立体图形?把它们画在一张硬纸片上,剪下来,折叠、粘贴,看看得到的图形和你想象的是否一样?
2.画出正方体的展开图.
归纳:
不是所有的立体图形都有展开图,如球;
由立体图形的展开图可识别出立体图形的形状,具体方法是:展开图中有圆,一般考虑圆柱或圆锥;展开图中有三角形,一般考虑棱柱或棱锥;展开图中有长方形或正方形,一般考虑棱柱;
正方体的展开图:
重点题型
题型一 从不同方向看集合体
1.桌上放着一个球和一个圆柱,下面a、b、c、d、e这五幅图分别是从什么方向看到的?题型二 简单几何体的展开图
2.一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面是( )
A.和 B.谐
C.沂 D.南
随堂训练
一个几何体从正面看、左面看、上面看都是正
方形,则这个立体图形是 .
2.从不同方向看到的一立体图形如图所示,那么
这个立体图形是 .
3.一个正方体中,截去一个小正方体的立体图如图所示,从左面观察这个图形,得到的平面图形是 ( )
4.如图所示的物体,从左面看得到的图是( )
A B C D
5.下面形状的四张纸板,按图中线经过折叠可以
围成一下直三棱柱的是 ( )
A B C D
6.下图中不是正方体的表面展开图的是 ( )
A B C D
7.分别从正面、左面、上面观察三棱柱和四棱锥,
看一看各能得到什么平面图形
能力提升
1.下面是一些立体图形的展开图,用它们能围 成什么样的立体图形?
2.正方体展开图如下,原正方体相对两个面上的数字之和的最小值的是 .
数学广角
动物中的数学“天才”
蜜蜂蜂房是严格的六角柱状体,它的一端是平整的六角形开口,另一端是封闭的六角菱锥形的底,由三个相同的菱形组成,组成底盘的菱形的钝角为109度28分,所有的锐角为70度32分,这样既坚固又省料,蜂房的巢壁厚0.073毫米,误差极少。
第四章 几何图形初步
4.1.2 点、线、面、体
学习目标
1.通过丰富的实例,进一步认识点、线、面、体的几何特征,感受它们之间的关系.
2.培养操作、观察、分析、猜测和概括等能力,同时渗透转化、化归、变换的思想.
自主预习
1.观察你使用的数学课本,它有几个面?面与面相交的地方形成了几条线?线与线相交成几个点?总结点、线、面、体的关系,并举出生活中另外一些实例说明这一关系.
2.找出生活中包含平面、曲面、直线、曲线、点的例子.
注意:
点、线、面是够成几何图像的基本元素,几何中点无大小(点是位置的标志),线无粗细,面无厚薄.
课堂探究
探究一 点、线、面、体
1.几何图形是由什么组成的?什么是构成图形的基本元素?
2.观察图形填空:
这是一个长方体模型,围成它的有 个面, 面与面相交的地方形成了 条线,线与线相交成 个点.
这是一个圆柱模型,围成它的有 个面, 面与面相交的地方形成了 条线.与长方体有 何不同?
归纳:
体是 围成的,面有 也有 ;面与面相交形成 ,线有 也有 ;线与线相交形成 ,点没有 ___________之分.
3.笔尖可以看作一个点,这个点在纸上运动时,形成了什么图形?想一想,从中你又有何发现?请用最简练的语言概括你的发现.
4.汽车雨刷可以看作一条线,它在挡风玻璃上来回摆动时有什么现象?
5.点动成线,线动成面.那么请同学们想一想,当面运动时会形成什么图形?如何验证你的猜想?
探究二 由平面图形旋转而成的立体图形
如图上面的平面图形绕轴旋转一周,可以得到下面的立体图形,把有对应关系的平面图形与立体图形用线连起来
重点题型
如图上面的平面图形绕轴旋转一周,可以得到下面的立体图形,把有对应关系的平面图形与立体图形用线连起来
随堂训练
1.请你用学到的数学知识解释下列现象:流星从空中划过留下的痕迹,说明了 .车轮转动时,看起来像一个整体的圆面,这说明了 .一枚硬币在光滑的桌面上快速旋转形成一个球,这说明了
2.如图所示的几何体由 个面围成,面与
面相交有 条线,直的线有 条,曲的
线有 _______条.
3.四棱锥有 个面,面与面相交形成了 ________条棱,这些棱相交形成了 个点.
4.将长方形按图中所示的四种方法旋转,能得到圆柱体是 _____.
5.如图,用第一行的图形绕轴旋转一周,便能形成第二行的某个几何体,请你用线连一连.
6.如图所示,要给这个长,宽,高分别为xcm,ycm,zcm的箱子打包,其打包方式如图所示,则打包带的长至少要多少?(用含x,y,z的代数式表示)
能力提升
现有一个长为8cm,宽为6cm的长方形,分别绕它的长、宽所在直线旋转一周,得到不同的圆柱体,它们的体积分别是多少?(结果用π表示).
数学广角
谜语“千条线万条线,落在水里看不见”,你能用数学知识解释这一现象吗?
第四章 几何图形初步
4.2直线、射线、线段(第1课时)
学习目标
1.认识直线、射线、线段的区别与联系,逐步掌握他们的表示方法.
2.结合实例,了解两点确定一条直线的基本事实,并逐步应用.
3.能根据语句画出相应的图形,会用语句描述简单的图形,在图形的基础上发展数学语言.
自主预习
1.硬纸条固定在硬板上至少需要几颗图钉?若将图钉抽象为点,纸条抽象成直线,你能得到什么结论?请画图说明.
2.如何表示直线、射线、线段.
3.怎样由图中的线段得到一条射线或一条直线.
课堂探究
探究一 直线公理
1.经过一点能画几条直线?经过两点能画几条直线?如下图画一画试一试.
归纳:
经过一点可以画____条直线;经过两点有___直线,并且_____直线(即两点确定一条直线).
探究二 直线、射线、线段的定义及表示
1.如图,直线有几种表示方法?如何表示?
2.如图,射线有几种表示方法?如何表示?
3.如图,线段有几种表示方法?如何表示?
4.在直线、射线、线段的表示法中,为什吗用两个大写字母表示?
归纳:
名称 不同点 联 系
图形 延伸方向 端点个数 度量
直线
射线
线段
5.用几何语言描述下列图形.
归纳:
点与直线有什么位置关系?
重点题型
题型一 按要求画图
1.如图平面上有四点A、B、C、D,按下列语句画图:
如图平面上有四点A、B、C、D (1)画直线AB、射线BC与线段DC;
(2)延长CD与直线AB相交于点E;
(3)画线段AC、BD交于点F;
(4)连接AD,并使其反向延长与射线CB交于点G.
题型二 射线、线段的条数的确定
2.根据图形,确定直线上射线和线段的条数,并归纳结论.
随堂训练
1.点与直线的位置关系有两种,分别是_________和__________.
2.用枪瞄准射击时,总是用一只眼对准准星和目标,用数学知识解释为 _______________.
3.下列说法:①直线的一半是射线;②射线AB和射线BA是同一条射线;③线段AB与线段BA是同一条线段;④直线AB和直线BA是同一条直线;⑤一条直线上一点把这条直线分成两条射线,其中正确的是________(填上序号即可).
4.下列写法中正确的是 ( )
A.直线a、b相交于点n
B.直线AB、CD相交于点M
C.直线ab、cd相交于点M
D.直线AB、CD相交于m
5.如图,在直线上依次有五个点A、B、C、D、E,则图中射线的条数为 ( )
A.2条 B.10条 C.5条 D.4条
6.如图,点A、B、C是直线m上的三个点,图中共有线段的条数是 ( )
A.1条 B.2条 C.3条 D.4条
7.下列语句正确的是 ( )
A.画直线AB=10厘米
B.延长射线OA
C.画射线OB=3厘米
D.延长线段AB到点C,使BC=AB
8.在直线m上有A、B、C三点,下列说法正确的有 ( )
①射线AB与射线BC是同一条射线;②直线AB经过点C;③射线AB与射线AC是同一条射线;④直线AB与直线BC是同一条直线.
A.1个 B.2个 C.3个 D.4个
能力提升
平面上有三点A、B、C,过其中每两点画直线,一共可画几条?四点呢?n个点呢?试画图说明.
数学广角
几何发展史
几何, 是由希腊文演变而来,其原意是土地测量。是埃及人创造的,并且产生于土地测量。由于尼罗河泛滥,经常冲毁界限,这样测量变成了必要的工作。无可置疑的,这类科学和其它科学一样,都发生于人类的需要。”明代徐光启(1562~1633)和天主教耶酥会传教士利玛窦翻译欧几里得的《几何原本》时将Geometry一词译为几何学。
第四章 几何图形初步
4.2直线、射线、线段(第2课时)
学习目标
1.会画一条线段等于已知线段.
2.结合图形认识线段间的数量关系,学会比较线段的大小,理解线段的和、差以及线段中点的意义.
3.理解两点间距离的意义,能度量两点间的距离.
自主预习
1.任意画线段,怎样再画一条与线段长度相等的线段
2.阅读课本,利用下图中的已知线段,分别画线段,线段,并谈谈你对线段的中点、三等分点、四等分点的认识.
课堂探究
探究一 线段的比较与和差
1.已知一条线段a,怎样画一条线段AB,使AB=a,动手画一画.
2.有两条线段,你能判断一下它们的长短吗?你有什么方法来验证你的判断?
归纳:
比较两条线段的方法:
3.已知线段a和b(a>b),怎样画一条线段AC=a+b 怎样画一条线段AD=a-b?动手画一画.
探究二 线段的中点、三等分点
1.什么是线段的中点?
2.线段的中点具有什么性质?
3.若AM=BM,则M是AB的中点吗?若AM=AB,BM=AB,则点M是AB的中点吗?
4.什么是线段的三等分点?具有什么性质?
探究三 线段的性质及两点的距离
1.如图,从A地到B地有四条道路,除它们之外能否再修一条从A地到B地的最短道路?
如果能,请联系你以前所学的知识,在图上画出最短线路.
归纳:
由问题1,你能得到什么结论?
2.什么叫两点的距离?
重点题型
题型一 线段间的数量关系及计算
1.如图所示,为线段的中点,为线段的中点,,求的长.
题型二 两点间距离
2.若点在线段上,=8cm,=5cm,,则,两点间的距离是( )
A.3cm B.13cm
C.3cm或13cm D.不确定
随堂训练
1.估计下列图形中、AC的大小关系,再用刻度尺或圆规检验你的估计.
2. 如图所示,已知线段,, 画一条线段,使它等于.
3.如图所示,点C是AB的中点,点D是BC的
点,则下列表达式:① ;②;③;④,其中正确的是______.(填上序号)
4.如图所示,已知,是的中点,,求,, 长.
能力提升
如图,线段,点是线段上一点,,分别是线段,的中点,小华据此轻松地求得.他在反思过程中突发奇想:若点运动到的延长线上,原有的结论“”是否依然成立?请帮小华画出图形并说明理由.
数学广角
蜗牛何时爬上井?
一只蜗牛不小心掉进了一口10米深的枯井里,它决心爬出去。它不停的爬呀,到了傍晚终于爬了5米。心想:“照这样的速度,明天傍晚我就能爬上去。”想着想着,它不知不觉地睡着了。早上,蜗牛发现睡着以后从井壁上滑下来4米。蜗牛叹了一口气,咬紧牙又开始往上爬。到了傍晚又往上爬了5米,可是晚上蜗牛又滑下4米。爬呀爬,最后坚强地蜗牛终于爬上了井台。小朋友你能猜出来,蜗牛需要
用几天时间就能爬上井台吗?
第四章 几何图形初步
4.3.1 角
学习目标
1.理解角的定义和相关概念,用运动的观点理解角、平角、周角等概念,掌握角的表示方法.
2.掌握角的度量及度量单位之间的转化.
自主预习
1.请举出几个生活中给我们角的形象的物体,根据你对角的理解,画出几个不同形状的角并指出角的两边是什么图形
2.指出图中的角的顶点和边,并用三种方法表示该角.
3.度、分、秒是常用的角的度量单位,它们之间的互化方法与时间单位间的互化方法类似,请你完成下列各题.
(1)1.45°等于多少分 等于多少秒
(2)900″等于多少分 等于多少度
课堂探究
探究一 角的概念和表示
1.有 的两条 组成的图形叫做角. ___ ____叫角的顶点,
叫角的边.
2.下面三个角各可以如何表示?写在对应角的下面.
3.角也可以看作由 绕着它的 旋转而形成的图形.如图,射线绕点旋转,当终止位置和起始位置 时,
形成的角是平角;继续旋转,和重合时,形成的角是 .
归纳:
(1)用三个大写字母表示角时,顶点字母必须写在 _____ .(2) 用一个大写字母表示角时,必须顶点处只有 个角.(3)用数字或希腊字母表示角时,必须在相应角的内部加弧线及数字(或希腊字母).
探究二 角的度量及转换
1.度、分、秒是常用的角的度量单位.把一个周角360等分,每一份就是 的角,记作;把1度的角60等分,每一份叫做1分的角,记作 ;把1分的角60等分,每一份就是1秒的角, 记作 .
2.1周角= °,1平角= °,
1°= ′, 1′= ″.
的度数是49度20分24秒,记作= .
3.()°= ′= ″;
5760″= ′= °.
归纳:
度、分、秒的转化是___进制,由度化分,由分化秒,需乘以___;由秒化分,由分化度,只要除以___即可.
重点题型
题型 角的表示
1.写出图中:
(1)能用一个字母表示的角;
(2)以B为顶点的角;
(3)图中共有几个角?
2.以点O为端点引4条射线,此时图中共有多少个角?怎样表示?
题型二 度、分、秒之间的换算
1.0.75°= ′= ″,
34.37°= ° ′ ″.
2.1 800″= °,39°36′= °
随堂训练
1.若∠α=30°18′,∠β=30.18°,∠γ=30.3°,则下列结论正确的是 ( )
A.∠α=∠β B.∠α=∠γ
C.∠β=∠γ D.∠α、∠β、∠γ互不相等
2.在钟表上,8时整,时针与分针所成的角是 ;l时30分时,时针与分针所成的角是 .
3.根据下列语句画图:
(1)画∠AOB=80°; (2)在∠AOB的内部画射线OC,使∠BOC=60°; (3)在∠AOB的外部画射线OD,使∠DOA=30°.
4.角的运算
(1)23°31′25″+42°27′56″;
(2)42°31′56″-23°37′;
(3)23°31′25″×3.
能力提升
如图以O为端点的射线共4条,其中任一条射线与其他3条射线都必构成一个角(小于平角的角),这样,可得4×3个角,但这些角中,每一个角都重复了一次,所以4条射线共组成角的个数为=6.
同理,如果从O点引5条射线(每两条射线不在同一直线上),那么以这个点为顶点的角的个数为 个;
如果从O点引n条射线(每两条射线不在同一直线上),那么以这个点为顶点的角的个数为 多少个?你能解释其中的道理吗
数学广角
动物中的数学“天才”
蜜蜂蜂房是严格的六角柱状体,它的一端是平整的六角形开口,另一端是封闭的六角菱锥形的底,由三个相同的菱形组成。组成底盘的菱形的钝角为109度28分,所有的锐角为70度32分,这样既坚固又省料。蜂房的巢壁厚0.073毫米,误差极小。
丹顶鹤总是成群结队迁飞,而且排成“人”字形。“人”字形的角度是110度。更精确地计算还表明“人”字形夹角的一半——即每边与鹤群前进方向的夹角为54度44分8秒!而金刚石结晶体的角度正好也是54度44分8秒!是巧合还是某种大自然的“默契”?
蜘蛛结的“八卦”形网,是既复杂又美丽的八角形几何图案,人们即使用直尺的圆规也很难画出像蜘蛛网那样匀称的图案。
第四章 几何图形初步
4.3.2 角的比较与运算
学习目标
1.会比较角的大小,理解两个角的和、差的意义.
2.掌握角平分线的概念;能够利用角平分线的定义来解决相关的计算问题.
自主预习
1.如何比较两条线段的大小 那么,你能比较两个角的大小吗 如图,已知∠ABC和∠DEF,试一试.
2.如图,回答下列问题:
(1)图中有多少个角 请你表示出这些角之间的关系;
(2)若∠AOB=120°,∠AOC=26°8′,求∠BOC的度数.
3.在透明纸上画一个∠AOB,如图,沿着顶点对折,使角的两边重合,折痕为0C,回答下列问题:
(1)用式子表示出∠AOB、∠AOC和∠BOC的数量关系;
(2)射线OC叫做什么
(3)若∠AOB=45°3′,求∠AOC的度数.(精确到分)
课堂探究
探究一 分类讨论解决角的和差问题
1.已知∠AOB =80°,∠AOC=40°,求∠BOC的度数.
问题1:按照题意画出图形;
问题2:∠AOB与∠AOC有怎样的位置关系;
问题3:∠AOB 、∠AOC和∠BOC之间有怎样的数量关系?
探究二 角平分线及性质
1.结合图形,说明什么是角平分线?
2.OC是∠AOB的角平分线,∠AOC、∠BOC与∠AOB之间有什么关系?
3.若∠AOC=∠BOC,则OC是角平分线吗?若∠AOC=∠AOB,则OC是角平分线吗?
4.什么是角的三等分线?按下图说明.
重点题型
题型一 角的和差
1.已知∠AOB=120°,∠BOC=30°,求∠AOC的度数.
题型二 角平分线
2.如图所示,OC是∠AOB平分线, 0D 平分∠AOC,且∠AOB=98°,
则∠COD为 ( )
A.24°30′ B.24°5 ′
C.2° D.30°
3.已知:如图,∠AOB=130°,OE平分∠BOC,OF平分∠AOC.求∠EOF的度数.
随堂训练
1.下列说法正确的是 ( )
A.两条射线就是一个周角
B.一条射线就是一个周角
C.角的两边越长,角就越大
D.一条射线绕着端点从起始位置旋转到终止位置所形成的图形叫做角
2.用放大5倍的放大镜看l0°的角,观察到的角的度数为 ( )
A.10° B.50° C.2° D.以上都不对
3.小亮利用星期天进行社会调查活动,早晨8:00出发, 中午12:30到家,问小亮到家时时针和分针的夹角为 ( )
A.85° B.150° C.180° D.165°
4.点D在∠AOB的内部,下列等式不能表示0D是角平分线的等式是 ( )
A.∠AOD=∠BOD B.∠AOD=∠BOD
C.∠AOD=∠AOB D.∠AOB=2∠BOD
5.计算:
(1)20°17′×6; (2)156°33′÷5.
6.用三角板画出105°,l35°的角.
能力提升
如图所示,0是直线AC上一点,0B是一条射线,OD平分∠AOB,0E在∠BOC内,∠BOE=∠E0C,∠DOE=70°,求∠EOC.
中考链接
1.(2012·广州)已知∠ABC=30°,BD是∠ABC的平分线,则∠ABD=________度.
2.(2012·北京)如图,直线,交于点,射线平分,若,则等于( )
A. B. C. D.
数学广角
1832年5月30日晨,在巴黎的葛拉塞尔湖附近躺着一个昏迷的年轻人,过路的农民从枪伤判断他是决斗后受了重伤,就把这个不知名的青年抬到医院。第二天早晨十点钟,他就离开了人世。数学史上最年轻、最有创造性的头脑停止了思考。人们说,他的死使数学发展推迟了好几十年。这个青年就是死时不满21岁的伽罗华。
第四章 几何图形初步
4.3.3 余角和补角
学习目标
1.认识一个角的余角和补角.
2.掌握余角和补角的性质.
3.了解方位角,能确定具体物体的方位,进一步渗透数形结合的思想.
自主预习
1.如果两个角的和是__________,那么这两个角叫做互为余角,其中一个角是另一个角的_____.
2.如果两个角的和是__________,那么这两个角叫做互为补角,其中一个角是另一个角的_____.
3.填下列表:
∠a ∠a的余角 ∠a的补角
45°
77°
62°2′
x°
结论:同一个锐角的补角比它的余角大_______.
4.和都是的补角,则__.
5.如果,则的关系 ,理由是 .
6.在点O 北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,则∠AOB的度数是( ) A. 100° B. 70° C. 180° D. 140°
课堂探究
探究一 余角和补角的定义及性质
1.画一个直角∠AOB和一个平角∠CPD,分别过两个角的顶点画射线ON、PM.
2.射线将直角和平角分成几部分?它们的度数关系如何?
3.将两个角拉开,它们的度数关系有变化吗?这说明什么问题?
归纳:
互为余角、互为补角的概念.
4.如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
归纳:
余角的性质:
5.如图, ∠1与∠2互补,∠3与∠4互补, ∠2= ∠3,那么∠1与∠4相等吗?为什么?
归纳:
补角的性质:
探究二 方位角
1.什么是方位角?
2.平面图形上的方向是怎么规定的?
3.在方位角的表示中把什么方向写在前,把什么方向写在后?
4.如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
重点题型
题型一 余角和补角的概念
1.若一个角的补角等于它的余角4倍,求这个角的度数.
题型二 余角和补角的性质
2.点 A、O、B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠COB,图中哪些角互为余角?
题型三 方位角应用
3.从A看B的方向是北偏东21°,那么B看A的方
向是( )
A.南偏东69° B.南偏西69°
C.南偏东21° D.南偏西21°
随堂训练
1.52°24′的余角是_______,补角是________.
2.射线OA方向是东北方向,射线OB方向是北偏西60°,则∠AOB度数是______.
3.己知∠α与∠β互余,且∠α=150 ,则∠β的补角为 度.
4.下列正确的有 ( )
⑴一个角的补角一定是钝角;⑵互补的两个角不可能相等;⑶若∠A+∠B+∠C=90 ,则∠A+∠B是∠C的余角;⑷∠A的补角与∠A的余角的差一定等于直角;⑸两个锐角一定互为余角;⑹直角没有补角,⑺如果∠MON=180 ,那么M、O、N三点在一条直线上.
A.1个 B.2个 C.3个 D.4个
5. 和北偏西40°的射线OA组成平角AOB的射线OB是 ( )
A.南偏东40°的射线 B.南偏东50°的射线
C.南偏东60°的射线 D.东南方向的射线
6.已知有一条射线OA,若从点O再引两条射线OB、OC,且∠AOB=72°,∠BOC=36°,则∠AOC的度数是 ( )
A.36° B.108° C.72°或36° D.36°或108°
7.如图,∠AOC=∠COB=90°,∠DOE=90°,A、O、B三点在一直线上
(1)写出∠COE的余角,∠AOE的补角;
(2)找出图中一对相等的角,并说明理由 .
能力提升
已知:如下图,点A、O、B在同一直线上,∠1与∠2互余,OE、OF分别是∠AOC、∠AOD的平分线,求∠EOF的度数.
中考链接
1.(2012·江苏泰州)已知∠α的补角是130°,则∠α= 度.
2.(2012·江西)如图 所示,如果在阳光下你的身影的方向北偏东60°方向,那么太阳相对于你的方向是( )
A. 南偏西60° B.南偏西30°
C.北偏东60° D.北偏东30°
数学广角
牛顿是举世公认的、有史以来最伟大的科学家之一。23毕业于著名的剑桥大学后留校工作。后因逃避伦敦流行的鼠疫来到母亲的农场里。在这里,他被一个常人熟视无睹的现象吸引住了。有一次,他看到一个熟透了的苹果落在地上,便开始思索为什么苹果会垂直落在地上,而不是飞到天上去呢?一定是有一种力在拉它,那么这种将苹果往下拉的力会不会控制月球?他就是通过这个看起来十分简单的现象,发现了著名的万有引力
●
建
设
和
谐
沂
南
z
x
y
A
B
a
b
A
B
(1)
(2)
(3)
A
B
C
A
A
B
B
C
C
a
b
