人教版七年级下册第5章相交线与平行线全章学案19页
文档属性
| 名称 | 人教版七年级下册第5章相交线与平行线全章学案19页 | 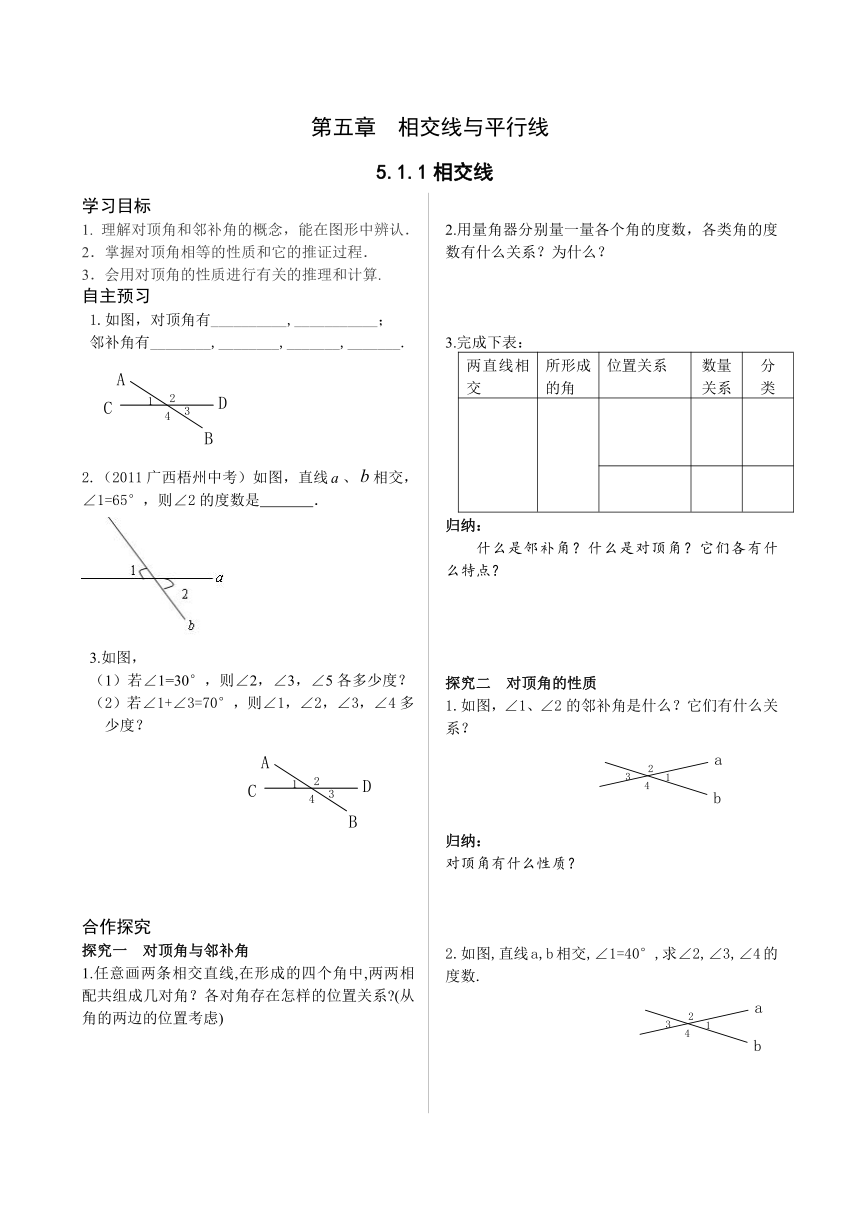 | |
| 格式 | zip | ||
| 文件大小 | 476.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-22 15:13:34 | ||
图片预览





文档简介
第五章 相交线与平行线
5.1.1相交线
学习目标
1. 理解对顶角和邻补角的概念,能在图形中辨认.
2.掌握对顶角相等的性质和它的推证过程.
3.会用对顶角的性质进行有关的推理和计算.
自主预习
1.如图,对顶角有__________,___________;
邻补角有________,________,_______,_______.
2.(2011广西梧州中考)如图,直线、相交,∠1=65°,则∠2的度数是 .
3.如图,
(1)若∠1=30°,则∠2,∠3,∠5各多少度?
(2)若∠1+∠3=70°,则∠1,∠2,∠3,∠4多少度?
合作探究
探究一 对顶角与邻补角
1.任意画两条相交直线,在形成的四个角中,两两相配共组成几对角?各对角存在怎样的位置关系 (从角的两边的位置考虑)
2.用量角器分别量一量各个角的度数,各类角的度数有什么关系?为什么?
3.完成下表:
两直线相交 所形成的角 位置关系 数量关系 分 类
归纳:
什么是邻补角?什么是对顶角?它们各有什么特点?
探究二 对顶角的性质
1.如图,∠1、∠2的邻补角是什么?它们有什么关系?
归纳:
对顶角有什么性质?
2.如图,直线a,b相交,∠1=40°,求∠2,∠3,∠4的度数.
重点题型
题型 利用对顶角邻补角的性质解题
如图,直线AB、CD相交于点O.
(1)若∠AOC+∠BOD=100°,求各角的度数.
(2)若∠BOC比∠AOC的2倍多33°,求各角的度数.
毛
随堂训练
1.下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个 C.3个 D.4个
2.如图所示,∠1和∠2是对顶角的图形有( )毛
A.1个 B.2个 C.3个 D.4个
3.如图所示,三条直线AB、CD、EF相交于一点O,则∠AOE+∠DOB+∠COF等于( )
A.150° B.180° C.210° D.120°
4.如图所示,直线AB,CD相交于点O,已知∠AOC=70°,OE把∠BOD分成两部分, 且∠BOE:∠EOD=2:3,求∠EOD的度数.
拓展提升
1.两直线相交,共形成几对对顶角?几对邻补角?
2.如图,3条直线两两相交,共有对对顶角?几对邻补角?4条直线两两相交呢?5条呢?n条呢?你能发现什么规律?
中考链接
1.(2012·北京中考) 如图,直线,交于点,射线平分,若,则等于( )
A. B. C. D.
2.(2011广西柳州中考)如图,在所标识的角中,互为对顶角的两个角是( )
A.∠2和∠3 B.∠1和∠3
C.∠1和∠4 D.∠1和
数学广角
七巧板是一种拼图游戏,它是用七块板,以各种不同的拼凑法来拼搭千变万化的形象图案. 将一块正方形的板按图所示分割成七块,就成了七巧板.用这七块板可以拼搭成几何图形,如三角形、平行四边形、不规则的多边形等;也可以拼成各种具体的人物形象,或者动物,如猫、狗、猪、马等,或者是桥、房子、宝塔,或者是一些中、英文字符号.
拼摆七巧板不仅能丰富人的闲暇生活,还能活跃人的形象思维,启发人的智慧.试试看自己动手做一副七巧板,看看能拼摆出多少图形来,据说可以有一千五百多种呢.
第五章 相交线与平行线
5.1.2垂线
学习目标
1. 掌握垂线、垂线段、点到直线的距离等概念,理解垂线的性质.
2.掌握过一点有且只有一条直线与已知直线垂直的结论.
3.会用三角板或量角器过一点画一条直线的垂线.
自主预习
1. 如图所示,∠BAC=90°,AD⊥BC,垂足为D,则下列的结论正确的是( )
(1)AB与AC互相垂直 (2)AD与AC互相垂直 (3)点C到AB的垂线段是AB (4)点A到BC的距离是线段AD (5)线段AB的长度是点B到AC的距离 (6)线段AB是点B到AC的距离.
A.2个 B.3个 C.4个 D.5个
第1题图 第3题图
2.下列说法正确的有( )
①在平面内,过直线上一点有且只有一条直线垂直于已知直线;
②在平面内,过直线外一点有且只有一条直线垂直于已知直线;
③在平面内,过一点可以任意画一条直线垂直于已知直线;
④在平面内,有且只有一条直线垂直于已知直线.
A.1个 B.2个 C.3个 D.4个
3.如图,AC⊥BC,C为垂足,CD⊥AB,D为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC= 6,那么点C到AB的距离是_______,点A到BC的距离是________,点B到CD 的距离是_____,A、B两点的距离是_________.
合作探究
探究一 垂线的有关概念
同学们把手中可以转动的两条相交的纸条进行转动,在转动的过程中,是否会出现四个角都相等的情况?如果会,那么每一个角都是多少度?
归纳:
当两直线相交所构成的四个角中有一个为___________时,称这两直线互相垂直.他们的交点叫做_____________.
探究二 垂线的性质
1. 垂线的画法
过一点画已知直线的垂线,可分三步:“一落”即让直角板的一条直角边落在已知直线上与已知直线重合;“二移”即沿直线移动三角板,使其另一条直角边经过已知点;“三画”即沿此直角边画直线,则这条直线就是已知直线的垂线.
2.演示:
归纳:
垂线有什么性质?
2. 垂线段最短
(1)画直线L,在L外取一点P;
(2)过P点作出PO⊥L,垂足为O;
(3)点A1,A2,A3……在L上,连接P A1、PA2、PA3……;
(4)用度量法比较线段PO、PA1、PA2、PA3……的大小,
(5)得出线段 最小.
归纳:
(1)连接直线外一点与直线上各点的所有线段中, .简单说成: .
(2)___________________,叫做点到直线的距离.
重点题型
题型一 垂线的概念
1.如图,已知,,垂足为O,OE是一条射线,且,求,的度数.
题型二 垂线段、点到直线的距离
2. 判断对错,并说明理由:.
(1)直线外一点与直线上的一点间的线段的长度是这一点到这条直线的距离.
(2)如图,线段AE是点A到直线BC的距离.
(3)如图,线段CD的长是点C到直线AB的距离.
2题图 3题图
3. 如图,利用三角尺,画出点A到BC的垂线段AE,画出点C到DA的垂线段CF.
随堂训练
1.过一点有且只有________直线与已知直线垂直.
2.画一条线段或射线的垂线,就是画它们________的垂线.
3.直线外一点到这条直线的_________,叫做点到直线的距离.
4.如图1所示,下列说法不正确的是( )毛
A.点B到AC的垂线段是线段AB;
B.点C到AB的垂线段是线段AC
C.线段AD是点D到BC的垂线段;
D.线段BD是点B到AD的垂线段.
5.如图所示,能表示点到直线(线段)的距离的线段有( )
A.2条 B.3条 C.4条 D.5条
6.如图所示,AD⊥BD,BC⊥CD,AB=acm,BC=bcm,则BD的范围是( )
A.大于acm B.小于bcm
C.大于acm或小于bcm D.大于bcm且小于acm
7.点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到 直线m的距离为( )
A.4cm B.2cm; C.小于2cm D.不大于2cm
8. 如图所示,直线AB,CD,EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=70°,求∠DOG的度数.
拓展提升
如图所示,O为直线AB上一点,∠AOC=∠BOC,OC是∠AOD的平分线. (1)求∠COD的度数;(2)判断OD与AB的位置关系,并说明理由.
中考链接
(2011广西梧州中考)如图,直线EO⊥CD,垂足为点O,AB平分∠EOD,则∠BOD的度数为( )
A.120° B.130° C.135° D.140°
第五章相 交线与平行线
5.1.3同位角、内错角、同旁内
学习目标
1.理解同位角、内错角、同旁内角的概念.
2.能够在较复杂的图形中正确识别它们,并能说出是哪两条直线被哪条直线所截形成的.
自主预习
1.如图,直线AB和CD被直线EF所截,在∠1,∠2,∠3和∠4中,同位角有 ,内错角有 ,同旁内角有 .
你能说出同位角、内错角、同旁内角在位置上各有什么特征吗?
2.如图所示,∠1和∠2是直线______和_____被直线_______所截而成的_____角,∠3和∠4是直线_____和_____被直线______所截而成的_____角,∠5和∠6是直线_______和______被直线_____所截而成的______角,∠2和∠6是直线______和______被直线_______所截而成的_____角,∠1的同位角有_____,∠4的内错角有______,∠6的同旁内角有_____.
合作探究
探究一 同位角、内错角、同旁内角的定义
如图,直线AB、CD与EF相交(或两条直线AB、CD被第三条直线EF所截,其中AB、CD称为被截线,EF称为截线)构成8个角.通常将这种图形称作为“三线八角”.
如图,观察∠1和∠5,∠4与∠8的位置有什么共同特点(从截线和被截线的位置)?
2.与此有相同位置关系的还有哪些角?
归纳:什么是同位角?
3.观察∠3和∠5,∠4与∠6的位置有什么共同特点(从截线和被截线的位置)?
归纳:什么是内错角?
4.观察∠3和∠6,∠5与∠4的位置有什么共同特点(从截线和被截线的位置)?
归纳:什么是同旁内角?
探究二 同位角、内错角、同旁内角的应用
1.如图,直线DE,BC被直线AB所截.
(1)∠1和∠2,∠1和∠3,∠1和∠4各是什么位置关系的角?
(2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和 ∠3互补吗?为什么?
2.如图,三条直线,,两两相交,试写出图中所有的同位角、内错角及同旁内角.
归纳:
辨认这三种角的方法:两个角公共边所在的直线是截线,其余两边所在的直线就是被截线.
重点题型
同位角、内错角、同旁内角辨认
如下图所示:
(1)∠1,∠2,∠3,∠4,∠5,∠6是直线 、______被第三条直线 所截而成的.
(2)∠2的同位角是 ,∠1的同位角是 .
(3)∠3的内错角是 __ ,∠4的内错角是 .
(4)∠6的同旁内角是 ,∠5的同旁内角是 .
(5)∠4与∠A是同旁内角吗?
随堂训练
1.在如图所示的四个图形中,∠1和∠2不是同位角的是( )
2.如图5.1—26,下列结论中正确的是( ).
A.l与5是同位角
B.5与2是对顶角
C.l与2是同旁内角
D.1与3是同位角
3.如图5.1—25,已知直线DE、BC被直线AB所截,那么l与4是 ,2与4是 ,3与4是 .
4.如图5.1—27,图中共有同旁内角( ).
A.2对 B.3对 C.4对 D.5对
5.如图5.1—28,(1)直线AB、DC被直线CE所截,C的同位角是 ,同旁内角是 ;
(2) 1与2是直线 和 被第三条直线 所截得的 角;
(3)直线AD与CB被AB所截,A的内错角是 ,A与ABC是 角;
(4)直线AD与CB被DB所截, 和 是内错角.
拓展提升
如图,∠1和∠2,∠3和∠4,∠2和∠3各是哪两条直线被哪一条直线所截形成的?它们各是什么位置关系的角?
数学广角
在中国古典神话小说《西游记》里,写道:十里长亭无客走,九重天上观星辰。八河船只皆收港,七千州县尽关门。 六宫五府回官宰,四海三江罢钓纶。两座楼头钟鼓响,一轮明月满乾坤。 这首诗从十、九、八、七,说到六、五、四、三、两、一,诗中嵌进全部十个数字,而且从大往小,倒过来数,成为别具一格的“倒数诗”,更增加了趣味。《西游记》是明代吴承恩著的,问世已有400多年。按照我们现在数学里的习惯,用阿拉伯数字把诗中的各个数写出来,顺次排成一串,成为 10 9 8 7 6 5 4 3 2 1\ 现在做一个数学小游戏:用上面写出的十个数,不打乱顺序,添加适当的数学符号,组成十个算式,使计算结果分别等于10、9、8、7、6、5、4、3、2、1。 要组成其中任意一个算式,是很容易的。要组成全套十个,就要动动脑筋。如果再使组成十个算式的手法有变化,就更有趣了。 2 可以组成很多满足条件的算式,下面是其中的一组。 10+9-8-7+6+5-4-3+2×1=10; (10+98+76)×5÷4÷(3+2)+1=9; (10+9+8-7)×6÷5÷4+3-2+1=8; (109-87)÷(6+5)+4+3-2×1=7; (10+9+8-7-6)×5-43-21=6; (10+9+8+7+6)÷5-4÷(3-2)+1=5; 10×9-87+65-43-21=4; (109-8+7)÷6-54÷3+2+1=3; (109+87-6)÷5-4-32×1=2; (10×9-87)÷(6×54-321)=1.
第五章 相交线与平行线
5.2.1平行线
学习目标
1.使学生掌握平行的概念 ,表示方法.
2.掌握平行的公理,并利用平行公理的应用.
自主预习
1.在同一平面内直线AB、CD满足下列条件,写出其对应的位置关系.
(1)AB与CD没有公共点,则直线AB与CD的位置关系是 ;
(2)AB与CD有且只有一个公共点,则直线AB与CD的位置关系是 .
2.同一平面内,两条直线的位置关系有两种: ____________和 .
3.直线AB与直线CD平行,记作 ________,读作 .
4.经过直线外一点, 与已知直线平行.
5.若直线a∥b,b∥c,则a c,
理由是 .
合作探究
探究一 平行线的概念
1.分别将木条a、b与木条c钉在一起,并把它们想象成两端可以无限延伸的三条直线.转动a,直线a从在c的左侧与直线b相交逐步变为在右侧与b相交.想象一下,在这个过程中,有没有直线a与直线b不相交的位置呢?
归纳:
在木条转动过程中,存在一个直线a与直线b不相交的位置,这时直线a与b互相___________,
记作____________.
2.平行线在生活中是很常见的,你还能举出其他一些例子吗?
归纳:
什么是平行线?
3. 同一平面内,两条直线的位置关系有几种?
探究二 平行公理及推论
1.在转动木条a的过程中,有几个位置使得a与b平行?如图,过点B画直线a的平行线,能画出几条?怎样过直线直线外一点画已知直线的平行线?
归纳:
通过观察和画图,可以体验一个基本事实
(平行公理):
_____________________________________
2.过点C画一条直线与直线a平行,它与上题中所画的直线b平行吗?
归纳:
通过画图,你发现了什么?
________________________________
________________________________.
也就是说:如果b∥a,c∥a,那么_________.
重点题型
题型一 画平行线
1.根据下列要求画图.
(1)如图(1)所示,过点P画PE∥OA,交OB于点E,过点P画PH∥OB,交OA于点H;
(2)如图(2)所示,过点C画CE∥DA,与AB交于点E,
过点C画CF∥DB,与AB的延长线交 于点F.
(1) (2)
题型二 平行公理的应用
2.若a∥b,b∥c,d与a相交,则d与b、d与c的位置关系是什么?
3. 若a∥b,c⊥a,则b与c的位置关系是什么?
随堂训练
1.下列说法中正确的是 ( )
A.两条不相交的直线叫做平行线
B.一条直线的平行线有且只有一条
C.若a∥b,a∥c,则b∥c
D.在同一平面内的两条射线,如果它们不相交,则 一定互相平行
2.a.b、c是平面上任意三条直线,交点可以有( )
A.1个或2个或3个 B.1个或2个
C.0个或l个或2个或3个 D.都不对
3.已知a∥b,c∥d,若由此得出b∥d,则a和c应满足 的关系是( )
A.在同一平面内 B.不相交
C.平行或重合 D.不在同一平面内
4.下列说法中错误的个数是( )
(1)过一点有且只有一条直线与已知直线平行;
(2)过一点有且只有一条直线与已知直线垂直;
(3)在同一平面内,两条直线的位置关系只有相交、平行两种;
(4)不相交的两条直线叫做平行线;
(5)有公共顶点且有一条公共边的两个角互为邻补角.
A.1个 B.2个 C 3个 D 4个
5.如图,AD∥BC,E是AB上
一点,过E作EF∥AD交CD
于F,则EF与BC的位置关
6.对于同一平面内的三条直线a、b、c,给出下列
5个论断:①a∥b;②b∥c;③a⊥b;④a∥c;
⑤a⊥c,以其中两个论断为条件,一个论断为结论,组成一个正确的判断是 .
7.观察如图所示的长方体.
(1)用符号表示下列
两棱的位置关系:
AB EF,
EA ___AB,HE HG,
AD BC;
(2)EF与BC所在的直线是两
条不相交的直线,它们
__平行线(填“是”或“不是”),
由此可知 ____________内,两条不相交的直线才能叫做平行线.
拓展提升
工人师傅在铺设电缆时,为了检验三条电缆是否平行,工人师傅只检查了其中两条电缆线是否与第三条电缆线平行即可,你认为这种做法正确吗 请用本节课所学知识做出合理的解释.
数学广角
平行号、平行且相等号
如果一条直线和一个平面没有公共点,那么就说这条直线和这个平面平行.直线l平行于平面α,记作:L∥α.
如果两个平面没有公共点,叫做两个平面互相平行.平面α平行于平面β,记作α∥β.
在平面几何里,像矩形,正方形,平行四边形等图形,它们的对边都具有既平行又相等的特点.我们把这种“平行并且相等”的线段,用符号“”表示,读作“平行且等于”。已知四边形ABCD是平行四边形,那么有ABCD。
第五章 相交线与平行线
5.2.2 平行线的判定
学习目标
掌握平行线的三个判定定理.
会用判定定理解答问题.
自主预习
1.如图所示,直线L1,L2被L3所截,要判定L1∥L2,请在括号内填上适当的判定方法.
(1)∵∠l=∠2,∴L1∥L2( );
(2)∵∠2=∠3,∴L1∥L2( );
(3)∵∠4+∠3=180°,
∴Ll∥L2 ( );
(4)∵∠3=∠5,∴L1∥L 2 ( ).
2.根据图,下列推理判断错误的是( )
A.因为∠l=∠2,所以c∥d
B.因为∠3=∠4,所以c∥d
C.因为∠l=∠3,所以c∥d
D.因为∠2=∠3,所以a∥b
课堂探究
探究一 平行线的判定
1.我们学过的判断平行线的方法有哪些?
2.想一想,过直线外一点P,画已知直线的平行线的方法.观察三角板的移动,你发现了什么?
由此可得到何种判定两直线平行的方法?
归纳:
两直线平行的判定方法1:
简单说成:
3.用符号语言表示:
4.已知:∠1=450 ,∠ 2=1350, l1∥l2吗?
思考:(1)∠2与∠4有什么关系?l1∥l2吗?
(2)∠3与∠4有什么关系?l1∥l2吗?
归纳:
两直线平行的判定方法2:
简单说成:
5.用符号语言表示:
归纳:
两直线平行的判定方法3:
简单说成:
6.用符号语言表示:
探究二 平行线判定的应用
在同一平面内,两条直线垂直于同一条直线,这两条直线平行吗?为什么?
归纳:
两直线平行的判定法:
重点题型
题型 平行线的判定
1.如图,如果∠l=∠E,那么 ∥ ,理由是 ;
如果∠3=∠B,那么 ∥ ,
理由是 ;
如果∠2=∠ ,那么AB∥CD;
理由是 ;
如果∠2=∠ ,那么AC∥DE.
理由是 .
2.如图,BE是AB的延长线.
由∠CBE=∠A可得 ∥ ,
依据是 ;
由∠CBE=∠C可得 ∥ ,
依据是 ;
由∠CBE+∠A=180°可得 ∥ ,
依据是 .
课堂训练
1.如图所示,点E在AC的延长线上,下列条件中不能判断BD∥AE的是 ( )
A.∠3=∠4 B.∠l=∠2
C.∠D=∠DCE D.∠D+∠ACD=180°
2.如图6,能判断直线AB∥CD的条件是( )
A.∠l=∠2 B.∠3=∠4
C.∠l+∠3=180° D.∠3+∠4=180°
3.如图7,直线a,b被直线c 所截,现给出下列四个条件:(1) ∠1=∠5; (2) ∠1=∠7;
(3) ∠2+∠3 =180°; (4) ∠4=∠7,
其中能判断 a∥b的条件是 ( )
A.(1)(2) B.(1)(3)
C.(1)(4) D.(3)(4)
图6 图7
4.如图,请完成下列各题.
(1)如果∠1= ,那么DE∥AC;
(2)如果∠1= ,那么EF∥BC;
(3)如果∠2+ =180°,那么AC∥ED;
(4)如果∠2+ =180°,那么AB∥DF.
5.如图,已知∠l=∠2,DE平分∠BDC,
DE交AB于点E,试说明AB∥CD.
拓展提升
如图,已知AC、BC分别平分∠QAB、∠ABN,
且∠1与∠2互余,试说明PQ∥MN.
中考链接
(2012·贵州贵阳中考)如图,已知∠1=∠2,则图中互相平行的线段是 .
第五章 相交线与平行线
5.3.1 平行线的性质
学习目标
1.掌握平行线的三条性质.
2.能运用三条性质进行简单的推理和计算.
3.理解平行线的性质和判定的区别.
自主预习
1.(2012·福州中考)如图所示,直线a∥b,
∠1=70°,那么∠2的度数是( )
A.50° B. 60° C.70° D. 80°
2.如图a∥b,写出相等的同位角: __
写出相等的内错角 _,
写出互补的同旁内角
3.如图a∥b,∠1=68°,那么:∠2的度数为
4 (2012·湖南张家界中考)如图所示,直线a、b被直线c所截,下列说法正确的是( )
A.当∠1=∠2时,一定有a∥b
B.当a∥b时,一定有∠1=∠2
C.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180° 时,一定有a∥b
课堂探究
探究一 平行线的三条性质
1.请画出下图进行实验观察.
设l1∥l2,l3与它们相交,请度量∠1和∠2的大小,你能发现什么关系?
请同学们再作出直线l4,再度量一下∠3和∠4的大小,你还能发现它们有什么关系?
归纳:
平行线性质1(公理):
__________________________________________.
简记为:__________________________________.
2.自学课本87—88页内容后,小组内合作交流,讨论以下问题;
(1) 已知:a∥b
求证:∠1=∠2
归纳:
你证明的命题用文字叙为 .
可以简单地叙为 .
3.已知:如图 a∥b,∠1,∠2是直线a和b被 直线c截出的同旁内角,
求证:∠1+∠2=180°.
归纳:
你证明的命题用文字叙为 .
可以简单地叙为 .
探究二 两条平行线的距离
1.如图,已知直线AB∥CD,E是直线CD上任意一点,过E向直线AB作垂线,垂足为F,这样做出的垂线段EF的长度是平行线的距离.
结论:两条平行线的距离处处相等,而不随垂线段的位置而改变.
2.已知直线m∥n,点A、B在直线
n上,点C、D在直线m上,试判断△ABC与△ABD的面积有什么关系?为什吗?
重点题型
题型 一 平行线性质的应用
1. 根据上图将下列几何语言补充完整
(1)∵AD∥ (已知)
∴∠A+∠ABC=180°( )
(2)∵AB∥ (已知)
∴∠4=∠ ( )
∠ABC=∠ ( )
题型二 两条平行线间的距离应用
2.如图,直线a∥b,点A、E、F在a上,点B、C、D在b,BC=EF,三角形ABC与三角形DEF的面积相等吗?为什么?
课堂训练
1.如图所示AB∥CD,∠C=1150,∠A= 250,则∠E的度数为( )
A.700 B.800 C.900 D.1000
2.如图所示a∥b,∠1=1050,∠2=1400 则∠3的度数为( )
A.750 B.650 C.550 D.500
3.如图所示AB∥CD,AC⊥BC,∠BAC=650, 则
∠BCD= .
4.如图已知AB∥CD∥EF,EG∥BD则图中和∠1相等的角有 .
5.已知:如图 AD∥BC, AB∥DC 求证:∠A=∠C.
6.已知:如图DE∥AB,∠1=∠A,求证:DF∥AC.
拓展提升
已知:如图,AB∥CD.试判断∠B、∠E与∠D的关系.
中考链接
1.(2012·四川广元)一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向上平行行驶,那么两个拐弯的角 度可能为 ( )
A. 先向左转130°,再向左转50°
B. 先向左转50°,再向右转50°
C. 先向左转50°,再向右转40°
D. 先向左转50°,再向左转40°
2.(2012临沂)如图,AB∥CD,DB⊥BC,∠1=40°,则∠2的度数是 ( )
A.40° B.50°C.60° D.140°
第五章 相交线与平行线
5.3.2 命题、定理、证明
学习目标
1.掌握命题的概念,并能分清命题的组成部分.
2.经历判断命题真假的过程,对命题的真假有一个初步的了解.
3.初步培养不同几何语言相互转化的能力.
自主预习
1.判断下列语句是不是命题
(1)延长线段AB ( )
(2)两条直线相交,只有一交点 ( )
(3)画线段AB的中点 ( )
(4)若|x|=2,则x=2 ( )
(5)角平分线是一条射线 ( )
2.分别指出下列各命题的题设和结论.
(1)如果a∥b,b∥c,那么a∥c.
___________________________________
(2)内错角相等,两直线平行.
___________________________________
(3)如果,垂足为O,
那么.
___________________________________
课堂探究
探究一 命题的概念
观察下面几句话,回答问题
(1)我是初一的学生
(2)对顶角相等
(3)请把窗户关上
(4)等式两边加上相同的数,结果仍是等式.
(5) 画∠AOB=300
(6) 两条直线相交有几个交点?
上面几句话中,是对某件事情做出判断的语句有_____________.
结论:
1.像这样_______一件事情的语句,叫做_______,正确的命题称为_______命题,错误的命题称为_______命题。
2.命题常可以写成“如果......那么......”的形式.“如果”后接的部分是________,“那么” 后接的部分是_________ .
探究二 定理的概念
判断下列语句是否是命题,并指出是真命题还是假命题
(1)同角的余角相等 ;
(2)不许大声说话;
(3)连接A、B两点;
(4)两点之间,线段最短;
(5)等式两边加上相同的数,结果仍是等式;
(6)对顶角不相等.
命题是:__________________________;
真命题是:________________________;
假命题是:________________________ .
结论:
定理是从公理或其他真命题出发,用逻辑推理的方法判断得到的____________.
探究三 证明
已知:如图AB⊥BC,BC⊥CD且∠1=∠2,
求证:BE∥CF
证明:
∵AB⊥BC,BC⊥CD(已知)
∴ = =90°
( )
∵∠1=∠2(已知)
∴ = (等式性质)
∴BE∥CF
( )
结论:
一个命题的正确性需要经过推理才能作出判断,这个推理过程叫作_______.
注意:
证明中的每一步推理都要有根据,不能“想当然”.这些根据,可以是__________也可以是学过的__________、__________、__________等.
重点题型
题型一 判断语句是否命题
1.判断下列语句是不是命题
(1)延长线段AB ( )
(2)两条直线相交,只有一交点 ( )
(3)画线段AB的中点 ( )
(4)若|x|=2,则x=2 ( )
(5)角平分线是一条射线 ( )
题型二 找出命题的题设与结论
2.指出下列命题的题设和结论:
(1)如果同旁内角互补,那么两直线平行.
题设是__________________________________
结论是__________________________________
(2)若a≠b,则a2≠b2.
题设是____________,
结论是_______________
3. 把下列命题改写成"如果…那么…"的形式:
(1)互补的两个角不可能都是锐角;
(2)垂直于同一条直线的两条直线平行;
(3)对顶角相等.
课堂训练
1.下列命题中,正确的个数是( )
①相等的角是对顶角;
②如果两个三角形的底边不同,高也不同,那么这两个三角形的面积不等;
③两条直线相交,只有一个交点;
④凡直角都相等;
⑤凡锐角都相等.
A.1个 B.2个 C.3个 D.5个
2.“等角的补角相等”的题设是 ,结论是 .
3.“一个平面内的两条直线必将这个平面分成四个部分”,该命题是______命题.
4.把下列命题改写成“如果……,那么……”的形式:
(1)平行于同一直线的两条直线平行.
(2)同角的余角相等.
(3)绝对值相等的两个数一定相等.
5.如图,已知直线a、b被直线c所截,在括号内为下面各小题的推理填上适当的根据:
(1)∵a∥b,
∴∠1=∠3
(_________________);
(2)∵∠1=∠3,
∴a∥b (_______________________ );
(3)∵a∥b,
∴∠1=∠2 (________________________);
(4)∵a∥b,
∴∠1+∠4=180 (______________________)
(5)∵∠1=∠2,
∴a∥b (_____________________);
(6)∵∠1+∠4=180 ,
∴a∥b (_____________________).
拓展提升
已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE.
证明:
∵AB∥CD(已知)
∴∠4=∠
( )
∵∠3=∠4(已知)
∴∠3=∠
( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF
( )
即:∠ =∠
∴∠3=∠
( )
∴AD∥BE
( )
第五章 相交线与平行线
5.4 平移
学习目标
1.了解平移的概念,会进行点的平移;
2.理解平移的性质,能解决简单的平移问题.
自主预习
1.下列哪个图形是由左图平移得到的 ( )
2.下列四组图形中,有一组中的两个图形经过平移其中一个能得到 另一个,这组图形是( )
课堂探究
探究一 平移的概念
如何在一张半透明的纸上,画出一排形状和大小如下图的雪人?
图(4)
分析:
可以把一张半透明的纸盖在图(5)上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三……
思考:
在所画出的相邻两个雪人中,找出三组对应点(例如,它们的鼻尖A与A′,帽顶B与B′,纽扣C与C′),连接这些对应点,观察得出的线段,它们的位置、长短有什么关系?
图(5)
可以发现:
AA′∥BB′∥CC′,并且AA′=BB′=CC′
归纳:
(1)把一个图形整体沿_______移动,会得到一个新的图形.新图形与原图形的形状和大小 _________.
(2) 新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点就是_______.连接各组对应点的线段_________.
(3)图形的这种移动,叫做____________.
探究二 平移引申
平移在我们日常生活中是很常见的,利用平移我们也可以做很多美丽的图案,认真观察下图
.
图(6)
归纳:
图形的平移不一定是水平的,也不一定是竖直的.
重点题型
题型 平移三角形
如下图,平移三角形ABC,使点A移动到A′,画出平移后的三角形A′B′C′
随堂训练
1.(2012甘肃白银)将如图所示的图案通过平移后可以得到的图案是( )
( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
2.(2012江西省)如图,有a、b、c三户家用电路接入电表,相邻电路的电线等距排列,则三户所用电线( )
( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
A.a户最长 B.b户最长
C.c户最长 D.三户一样长
3.(2012·浙江义乌)如图所示,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.6 B.8 C.10 D.12
能力提升
三角形ABC在网格中如图所示,请根据下列提示作图
(1)向上平移2个单位长度.
(2)再向右移3个单位长度.
中考链接
1.(2012·福建莆田中考)如图,△A’B’C’是由 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )ABC沿射线AC方向平移2 cm得到,若AC=3cm,则A’C= cm.
( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
2.(2012·湖北宜昌中考)如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )
( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
A.先把△ABC向左平移5个单位,再向下平移2个单位
B.先把△ABC向右平移5个单位,再向下平移2个单位
C.先把△ABC向左平移5个单位,再向上平移2个单位
D.先把△ABC向右平移5个单位,再向上平移2个单位
A
D
B
C
1
2
C
A
B
D
E
F
1
2
A
D
B
C
E
F
1
2
3
4
B′
B
A
C
A′
C′
A
B
C
D
E
F
PAGE
5.1.1相交线
学习目标
1. 理解对顶角和邻补角的概念,能在图形中辨认.
2.掌握对顶角相等的性质和它的推证过程.
3.会用对顶角的性质进行有关的推理和计算.
自主预习
1.如图,对顶角有__________,___________;
邻补角有________,________,_______,_______.
2.(2011广西梧州中考)如图,直线、相交,∠1=65°,则∠2的度数是 .
3.如图,
(1)若∠1=30°,则∠2,∠3,∠5各多少度?
(2)若∠1+∠3=70°,则∠1,∠2,∠3,∠4多少度?
合作探究
探究一 对顶角与邻补角
1.任意画两条相交直线,在形成的四个角中,两两相配共组成几对角?各对角存在怎样的位置关系 (从角的两边的位置考虑)
2.用量角器分别量一量各个角的度数,各类角的度数有什么关系?为什么?
3.完成下表:
两直线相交 所形成的角 位置关系 数量关系 分 类
归纳:
什么是邻补角?什么是对顶角?它们各有什么特点?
探究二 对顶角的性质
1.如图,∠1、∠2的邻补角是什么?它们有什么关系?
归纳:
对顶角有什么性质?
2.如图,直线a,b相交,∠1=40°,求∠2,∠3,∠4的度数.
重点题型
题型 利用对顶角邻补角的性质解题
如图,直线AB、CD相交于点O.
(1)若∠AOC+∠BOD=100°,求各角的度数.
(2)若∠BOC比∠AOC的2倍多33°,求各角的度数.
毛
随堂训练
1.下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个 C.3个 D.4个
2.如图所示,∠1和∠2是对顶角的图形有( )毛
A.1个 B.2个 C.3个 D.4个
3.如图所示,三条直线AB、CD、EF相交于一点O,则∠AOE+∠DOB+∠COF等于( )
A.150° B.180° C.210° D.120°
4.如图所示,直线AB,CD相交于点O,已知∠AOC=70°,OE把∠BOD分成两部分, 且∠BOE:∠EOD=2:3,求∠EOD的度数.
拓展提升
1.两直线相交,共形成几对对顶角?几对邻补角?
2.如图,3条直线两两相交,共有对对顶角?几对邻补角?4条直线两两相交呢?5条呢?n条呢?你能发现什么规律?
中考链接
1.(2012·北京中考) 如图,直线,交于点,射线平分,若,则等于( )
A. B. C. D.
2.(2011广西柳州中考)如图,在所标识的角中,互为对顶角的两个角是( )
A.∠2和∠3 B.∠1和∠3
C.∠1和∠4 D.∠1和
数学广角
七巧板是一种拼图游戏,它是用七块板,以各种不同的拼凑法来拼搭千变万化的形象图案. 将一块正方形的板按图所示分割成七块,就成了七巧板.用这七块板可以拼搭成几何图形,如三角形、平行四边形、不规则的多边形等;也可以拼成各种具体的人物形象,或者动物,如猫、狗、猪、马等,或者是桥、房子、宝塔,或者是一些中、英文字符号.
拼摆七巧板不仅能丰富人的闲暇生活,还能活跃人的形象思维,启发人的智慧.试试看自己动手做一副七巧板,看看能拼摆出多少图形来,据说可以有一千五百多种呢.
第五章 相交线与平行线
5.1.2垂线
学习目标
1. 掌握垂线、垂线段、点到直线的距离等概念,理解垂线的性质.
2.掌握过一点有且只有一条直线与已知直线垂直的结论.
3.会用三角板或量角器过一点画一条直线的垂线.
自主预习
1. 如图所示,∠BAC=90°,AD⊥BC,垂足为D,则下列的结论正确的是( )
(1)AB与AC互相垂直 (2)AD与AC互相垂直 (3)点C到AB的垂线段是AB (4)点A到BC的距离是线段AD (5)线段AB的长度是点B到AC的距离 (6)线段AB是点B到AC的距离.
A.2个 B.3个 C.4个 D.5个
第1题图 第3题图
2.下列说法正确的有( )
①在平面内,过直线上一点有且只有一条直线垂直于已知直线;
②在平面内,过直线外一点有且只有一条直线垂直于已知直线;
③在平面内,过一点可以任意画一条直线垂直于已知直线;
④在平面内,有且只有一条直线垂直于已知直线.
A.1个 B.2个 C.3个 D.4个
3.如图,AC⊥BC,C为垂足,CD⊥AB,D为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC= 6,那么点C到AB的距离是_______,点A到BC的距离是________,点B到CD 的距离是_____,A、B两点的距离是_________.
合作探究
探究一 垂线的有关概念
同学们把手中可以转动的两条相交的纸条进行转动,在转动的过程中,是否会出现四个角都相等的情况?如果会,那么每一个角都是多少度?
归纳:
当两直线相交所构成的四个角中有一个为___________时,称这两直线互相垂直.他们的交点叫做_____________.
探究二 垂线的性质
1. 垂线的画法
过一点画已知直线的垂线,可分三步:“一落”即让直角板的一条直角边落在已知直线上与已知直线重合;“二移”即沿直线移动三角板,使其另一条直角边经过已知点;“三画”即沿此直角边画直线,则这条直线就是已知直线的垂线.
2.演示:
归纳:
垂线有什么性质?
2. 垂线段最短
(1)画直线L,在L外取一点P;
(2)过P点作出PO⊥L,垂足为O;
(3)点A1,A2,A3……在L上,连接P A1、PA2、PA3……;
(4)用度量法比较线段PO、PA1、PA2、PA3……的大小,
(5)得出线段 最小.
归纳:
(1)连接直线外一点与直线上各点的所有线段中, .简单说成: .
(2)___________________,叫做点到直线的距离.
重点题型
题型一 垂线的概念
1.如图,已知,,垂足为O,OE是一条射线,且,求,的度数.
题型二 垂线段、点到直线的距离
2. 判断对错,并说明理由:.
(1)直线外一点与直线上的一点间的线段的长度是这一点到这条直线的距离.
(2)如图,线段AE是点A到直线BC的距离.
(3)如图,线段CD的长是点C到直线AB的距离.
2题图 3题图
3. 如图,利用三角尺,画出点A到BC的垂线段AE,画出点C到DA的垂线段CF.
随堂训练
1.过一点有且只有________直线与已知直线垂直.
2.画一条线段或射线的垂线,就是画它们________的垂线.
3.直线外一点到这条直线的_________,叫做点到直线的距离.
4.如图1所示,下列说法不正确的是( )毛
A.点B到AC的垂线段是线段AB;
B.点C到AB的垂线段是线段AC
C.线段AD是点D到BC的垂线段;
D.线段BD是点B到AD的垂线段.
5.如图所示,能表示点到直线(线段)的距离的线段有( )
A.2条 B.3条 C.4条 D.5条
6.如图所示,AD⊥BD,BC⊥CD,AB=acm,BC=bcm,则BD的范围是( )
A.大于acm B.小于bcm
C.大于acm或小于bcm D.大于bcm且小于acm
7.点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到 直线m的距离为( )
A.4cm B.2cm; C.小于2cm D.不大于2cm
8. 如图所示,直线AB,CD,EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=70°,求∠DOG的度数.
拓展提升
如图所示,O为直线AB上一点,∠AOC=∠BOC,OC是∠AOD的平分线. (1)求∠COD的度数;(2)判断OD与AB的位置关系,并说明理由.
中考链接
(2011广西梧州中考)如图,直线EO⊥CD,垂足为点O,AB平分∠EOD,则∠BOD的度数为( )
A.120° B.130° C.135° D.140°
第五章相 交线与平行线
5.1.3同位角、内错角、同旁内
学习目标
1.理解同位角、内错角、同旁内角的概念.
2.能够在较复杂的图形中正确识别它们,并能说出是哪两条直线被哪条直线所截形成的.
自主预习
1.如图,直线AB和CD被直线EF所截,在∠1,∠2,∠3和∠4中,同位角有 ,内错角有 ,同旁内角有 .
你能说出同位角、内错角、同旁内角在位置上各有什么特征吗?
2.如图所示,∠1和∠2是直线______和_____被直线_______所截而成的_____角,∠3和∠4是直线_____和_____被直线______所截而成的_____角,∠5和∠6是直线_______和______被直线_____所截而成的______角,∠2和∠6是直线______和______被直线_______所截而成的_____角,∠1的同位角有_____,∠4的内错角有______,∠6的同旁内角有_____.
合作探究
探究一 同位角、内错角、同旁内角的定义
如图,直线AB、CD与EF相交(或两条直线AB、CD被第三条直线EF所截,其中AB、CD称为被截线,EF称为截线)构成8个角.通常将这种图形称作为“三线八角”.
如图,观察∠1和∠5,∠4与∠8的位置有什么共同特点(从截线和被截线的位置)?
2.与此有相同位置关系的还有哪些角?
归纳:什么是同位角?
3.观察∠3和∠5,∠4与∠6的位置有什么共同特点(从截线和被截线的位置)?
归纳:什么是内错角?
4.观察∠3和∠6,∠5与∠4的位置有什么共同特点(从截线和被截线的位置)?
归纳:什么是同旁内角?
探究二 同位角、内错角、同旁内角的应用
1.如图,直线DE,BC被直线AB所截.
(1)∠1和∠2,∠1和∠3,∠1和∠4各是什么位置关系的角?
(2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和 ∠3互补吗?为什么?
2.如图,三条直线,,两两相交,试写出图中所有的同位角、内错角及同旁内角.
归纳:
辨认这三种角的方法:两个角公共边所在的直线是截线,其余两边所在的直线就是被截线.
重点题型
同位角、内错角、同旁内角辨认
如下图所示:
(1)∠1,∠2,∠3,∠4,∠5,∠6是直线 、______被第三条直线 所截而成的.
(2)∠2的同位角是 ,∠1的同位角是 .
(3)∠3的内错角是 __ ,∠4的内错角是 .
(4)∠6的同旁内角是 ,∠5的同旁内角是 .
(5)∠4与∠A是同旁内角吗?
随堂训练
1.在如图所示的四个图形中,∠1和∠2不是同位角的是( )
2.如图5.1—26,下列结论中正确的是( ).
A.l与5是同位角
B.5与2是对顶角
C.l与2是同旁内角
D.1与3是同位角
3.如图5.1—25,已知直线DE、BC被直线AB所截,那么l与4是 ,2与4是 ,3与4是 .
4.如图5.1—27,图中共有同旁内角( ).
A.2对 B.3对 C.4对 D.5对
5.如图5.1—28,(1)直线AB、DC被直线CE所截,C的同位角是 ,同旁内角是 ;
(2) 1与2是直线 和 被第三条直线 所截得的 角;
(3)直线AD与CB被AB所截,A的内错角是 ,A与ABC是 角;
(4)直线AD与CB被DB所截, 和 是内错角.
拓展提升
如图,∠1和∠2,∠3和∠4,∠2和∠3各是哪两条直线被哪一条直线所截形成的?它们各是什么位置关系的角?
数学广角
在中国古典神话小说《西游记》里,写道:十里长亭无客走,九重天上观星辰。八河船只皆收港,七千州县尽关门。 六宫五府回官宰,四海三江罢钓纶。两座楼头钟鼓响,一轮明月满乾坤。 这首诗从十、九、八、七,说到六、五、四、三、两、一,诗中嵌进全部十个数字,而且从大往小,倒过来数,成为别具一格的“倒数诗”,更增加了趣味。《西游记》是明代吴承恩著的,问世已有400多年。按照我们现在数学里的习惯,用阿拉伯数字把诗中的各个数写出来,顺次排成一串,成为 10 9 8 7 6 5 4 3 2 1\ 现在做一个数学小游戏:用上面写出的十个数,不打乱顺序,添加适当的数学符号,组成十个算式,使计算结果分别等于10、9、8、7、6、5、4、3、2、1。 要组成其中任意一个算式,是很容易的。要组成全套十个,就要动动脑筋。如果再使组成十个算式的手法有变化,就更有趣了。 2 可以组成很多满足条件的算式,下面是其中的一组。 10+9-8-7+6+5-4-3+2×1=10; (10+98+76)×5÷4÷(3+2)+1=9; (10+9+8-7)×6÷5÷4+3-2+1=8; (109-87)÷(6+5)+4+3-2×1=7; (10+9+8-7-6)×5-43-21=6; (10+9+8+7+6)÷5-4÷(3-2)+1=5; 10×9-87+65-43-21=4; (109-8+7)÷6-54÷3+2+1=3; (109+87-6)÷5-4-32×1=2; (10×9-87)÷(6×54-321)=1.
第五章 相交线与平行线
5.2.1平行线
学习目标
1.使学生掌握平行的概念 ,表示方法.
2.掌握平行的公理,并利用平行公理的应用.
自主预习
1.在同一平面内直线AB、CD满足下列条件,写出其对应的位置关系.
(1)AB与CD没有公共点,则直线AB与CD的位置关系是 ;
(2)AB与CD有且只有一个公共点,则直线AB与CD的位置关系是 .
2.同一平面内,两条直线的位置关系有两种: ____________和 .
3.直线AB与直线CD平行,记作 ________,读作 .
4.经过直线外一点, 与已知直线平行.
5.若直线a∥b,b∥c,则a c,
理由是 .
合作探究
探究一 平行线的概念
1.分别将木条a、b与木条c钉在一起,并把它们想象成两端可以无限延伸的三条直线.转动a,直线a从在c的左侧与直线b相交逐步变为在右侧与b相交.想象一下,在这个过程中,有没有直线a与直线b不相交的位置呢?
归纳:
在木条转动过程中,存在一个直线a与直线b不相交的位置,这时直线a与b互相___________,
记作____________.
2.平行线在生活中是很常见的,你还能举出其他一些例子吗?
归纳:
什么是平行线?
3. 同一平面内,两条直线的位置关系有几种?
探究二 平行公理及推论
1.在转动木条a的过程中,有几个位置使得a与b平行?如图,过点B画直线a的平行线,能画出几条?怎样过直线直线外一点画已知直线的平行线?
归纳:
通过观察和画图,可以体验一个基本事实
(平行公理):
_____________________________________
2.过点C画一条直线与直线a平行,它与上题中所画的直线b平行吗?
归纳:
通过画图,你发现了什么?
________________________________
________________________________.
也就是说:如果b∥a,c∥a,那么_________.
重点题型
题型一 画平行线
1.根据下列要求画图.
(1)如图(1)所示,过点P画PE∥OA,交OB于点E,过点P画PH∥OB,交OA于点H;
(2)如图(2)所示,过点C画CE∥DA,与AB交于点E,
过点C画CF∥DB,与AB的延长线交 于点F.
(1) (2)
题型二 平行公理的应用
2.若a∥b,b∥c,d与a相交,则d与b、d与c的位置关系是什么?
3. 若a∥b,c⊥a,则b与c的位置关系是什么?
随堂训练
1.下列说法中正确的是 ( )
A.两条不相交的直线叫做平行线
B.一条直线的平行线有且只有一条
C.若a∥b,a∥c,则b∥c
D.在同一平面内的两条射线,如果它们不相交,则 一定互相平行
2.a.b、c是平面上任意三条直线,交点可以有( )
A.1个或2个或3个 B.1个或2个
C.0个或l个或2个或3个 D.都不对
3.已知a∥b,c∥d,若由此得出b∥d,则a和c应满足 的关系是( )
A.在同一平面内 B.不相交
C.平行或重合 D.不在同一平面内
4.下列说法中错误的个数是( )
(1)过一点有且只有一条直线与已知直线平行;
(2)过一点有且只有一条直线与已知直线垂直;
(3)在同一平面内,两条直线的位置关系只有相交、平行两种;
(4)不相交的两条直线叫做平行线;
(5)有公共顶点且有一条公共边的两个角互为邻补角.
A.1个 B.2个 C 3个 D 4个
5.如图,AD∥BC,E是AB上
一点,过E作EF∥AD交CD
于F,则EF与BC的位置关
6.对于同一平面内的三条直线a、b、c,给出下列
5个论断:①a∥b;②b∥c;③a⊥b;④a∥c;
⑤a⊥c,以其中两个论断为条件,一个论断为结论,组成一个正确的判断是 .
7.观察如图所示的长方体.
(1)用符号表示下列
两棱的位置关系:
AB EF,
EA ___AB,HE HG,
AD BC;
(2)EF与BC所在的直线是两
条不相交的直线,它们
__平行线(填“是”或“不是”),
由此可知 ____________内,两条不相交的直线才能叫做平行线.
拓展提升
工人师傅在铺设电缆时,为了检验三条电缆是否平行,工人师傅只检查了其中两条电缆线是否与第三条电缆线平行即可,你认为这种做法正确吗 请用本节课所学知识做出合理的解释.
数学广角
平行号、平行且相等号
如果一条直线和一个平面没有公共点,那么就说这条直线和这个平面平行.直线l平行于平面α,记作:L∥α.
如果两个平面没有公共点,叫做两个平面互相平行.平面α平行于平面β,记作α∥β.
在平面几何里,像矩形,正方形,平行四边形等图形,它们的对边都具有既平行又相等的特点.我们把这种“平行并且相等”的线段,用符号“”表示,读作“平行且等于”。已知四边形ABCD是平行四边形,那么有ABCD。
第五章 相交线与平行线
5.2.2 平行线的判定
学习目标
掌握平行线的三个判定定理.
会用判定定理解答问题.
自主预习
1.如图所示,直线L1,L2被L3所截,要判定L1∥L2,请在括号内填上适当的判定方法.
(1)∵∠l=∠2,∴L1∥L2( );
(2)∵∠2=∠3,∴L1∥L2( );
(3)∵∠4+∠3=180°,
∴Ll∥L2 ( );
(4)∵∠3=∠5,∴L1∥L 2 ( ).
2.根据图,下列推理判断错误的是( )
A.因为∠l=∠2,所以c∥d
B.因为∠3=∠4,所以c∥d
C.因为∠l=∠3,所以c∥d
D.因为∠2=∠3,所以a∥b
课堂探究
探究一 平行线的判定
1.我们学过的判断平行线的方法有哪些?
2.想一想,过直线外一点P,画已知直线的平行线的方法.观察三角板的移动,你发现了什么?
由此可得到何种判定两直线平行的方法?
归纳:
两直线平行的判定方法1:
简单说成:
3.用符号语言表示:
4.已知:∠1=450 ,∠ 2=1350, l1∥l2吗?
思考:(1)∠2与∠4有什么关系?l1∥l2吗?
(2)∠3与∠4有什么关系?l1∥l2吗?
归纳:
两直线平行的判定方法2:
简单说成:
5.用符号语言表示:
归纳:
两直线平行的判定方法3:
简单说成:
6.用符号语言表示:
探究二 平行线判定的应用
在同一平面内,两条直线垂直于同一条直线,这两条直线平行吗?为什么?
归纳:
两直线平行的判定法:
重点题型
题型 平行线的判定
1.如图,如果∠l=∠E,那么 ∥ ,理由是 ;
如果∠3=∠B,那么 ∥ ,
理由是 ;
如果∠2=∠ ,那么AB∥CD;
理由是 ;
如果∠2=∠ ,那么AC∥DE.
理由是 .
2.如图,BE是AB的延长线.
由∠CBE=∠A可得 ∥ ,
依据是 ;
由∠CBE=∠C可得 ∥ ,
依据是 ;
由∠CBE+∠A=180°可得 ∥ ,
依据是 .
课堂训练
1.如图所示,点E在AC的延长线上,下列条件中不能判断BD∥AE的是 ( )
A.∠3=∠4 B.∠l=∠2
C.∠D=∠DCE D.∠D+∠ACD=180°
2.如图6,能判断直线AB∥CD的条件是( )
A.∠l=∠2 B.∠3=∠4
C.∠l+∠3=180° D.∠3+∠4=180°
3.如图7,直线a,b被直线c 所截,现给出下列四个条件:(1) ∠1=∠5; (2) ∠1=∠7;
(3) ∠2+∠3 =180°; (4) ∠4=∠7,
其中能判断 a∥b的条件是 ( )
A.(1)(2) B.(1)(3)
C.(1)(4) D.(3)(4)
图6 图7
4.如图,请完成下列各题.
(1)如果∠1= ,那么DE∥AC;
(2)如果∠1= ,那么EF∥BC;
(3)如果∠2+ =180°,那么AC∥ED;
(4)如果∠2+ =180°,那么AB∥DF.
5.如图,已知∠l=∠2,DE平分∠BDC,
DE交AB于点E,试说明AB∥CD.
拓展提升
如图,已知AC、BC分别平分∠QAB、∠ABN,
且∠1与∠2互余,试说明PQ∥MN.
中考链接
(2012·贵州贵阳中考)如图,已知∠1=∠2,则图中互相平行的线段是 .
第五章 相交线与平行线
5.3.1 平行线的性质
学习目标
1.掌握平行线的三条性质.
2.能运用三条性质进行简单的推理和计算.
3.理解平行线的性质和判定的区别.
自主预习
1.(2012·福州中考)如图所示,直线a∥b,
∠1=70°,那么∠2的度数是( )
A.50° B. 60° C.70° D. 80°
2.如图a∥b,写出相等的同位角: __
写出相等的内错角 _,
写出互补的同旁内角
3.如图a∥b,∠1=68°,那么:∠2的度数为
4 (2012·湖南张家界中考)如图所示,直线a、b被直线c所截,下列说法正确的是( )
A.当∠1=∠2时,一定有a∥b
B.当a∥b时,一定有∠1=∠2
C.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180° 时,一定有a∥b
课堂探究
探究一 平行线的三条性质
1.请画出下图进行实验观察.
设l1∥l2,l3与它们相交,请度量∠1和∠2的大小,你能发现什么关系?
请同学们再作出直线l4,再度量一下∠3和∠4的大小,你还能发现它们有什么关系?
归纳:
平行线性质1(公理):
__________________________________________.
简记为:__________________________________.
2.自学课本87—88页内容后,小组内合作交流,讨论以下问题;
(1) 已知:a∥b
求证:∠1=∠2
归纳:
你证明的命题用文字叙为 .
可以简单地叙为 .
3.已知:如图 a∥b,∠1,∠2是直线a和b被 直线c截出的同旁内角,
求证:∠1+∠2=180°.
归纳:
你证明的命题用文字叙为 .
可以简单地叙为 .
探究二 两条平行线的距离
1.如图,已知直线AB∥CD,E是直线CD上任意一点,过E向直线AB作垂线,垂足为F,这样做出的垂线段EF的长度是平行线的距离.
结论:两条平行线的距离处处相等,而不随垂线段的位置而改变.
2.已知直线m∥n,点A、B在直线
n上,点C、D在直线m上,试判断△ABC与△ABD的面积有什么关系?为什吗?
重点题型
题型 一 平行线性质的应用
1. 根据上图将下列几何语言补充完整
(1)∵AD∥ (已知)
∴∠A+∠ABC=180°( )
(2)∵AB∥ (已知)
∴∠4=∠ ( )
∠ABC=∠ ( )
题型二 两条平行线间的距离应用
2.如图,直线a∥b,点A、E、F在a上,点B、C、D在b,BC=EF,三角形ABC与三角形DEF的面积相等吗?为什么?
课堂训练
1.如图所示AB∥CD,∠C=1150,∠A= 250,则∠E的度数为( )
A.700 B.800 C.900 D.1000
2.如图所示a∥b,∠1=1050,∠2=1400 则∠3的度数为( )
A.750 B.650 C.550 D.500
3.如图所示AB∥CD,AC⊥BC,∠BAC=650, 则
∠BCD= .
4.如图已知AB∥CD∥EF,EG∥BD则图中和∠1相等的角有 .
5.已知:如图 AD∥BC, AB∥DC 求证:∠A=∠C.
6.已知:如图DE∥AB,∠1=∠A,求证:DF∥AC.
拓展提升
已知:如图,AB∥CD.试判断∠B、∠E与∠D的关系.
中考链接
1.(2012·四川广元)一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向上平行行驶,那么两个拐弯的角 度可能为 ( )
A. 先向左转130°,再向左转50°
B. 先向左转50°,再向右转50°
C. 先向左转50°,再向右转40°
D. 先向左转50°,再向左转40°
2.(2012临沂)如图,AB∥CD,DB⊥BC,∠1=40°,则∠2的度数是 ( )
A.40° B.50°C.60° D.140°
第五章 相交线与平行线
5.3.2 命题、定理、证明
学习目标
1.掌握命题的概念,并能分清命题的组成部分.
2.经历判断命题真假的过程,对命题的真假有一个初步的了解.
3.初步培养不同几何语言相互转化的能力.
自主预习
1.判断下列语句是不是命题
(1)延长线段AB ( )
(2)两条直线相交,只有一交点 ( )
(3)画线段AB的中点 ( )
(4)若|x|=2,则x=2 ( )
(5)角平分线是一条射线 ( )
2.分别指出下列各命题的题设和结论.
(1)如果a∥b,b∥c,那么a∥c.
___________________________________
(2)内错角相等,两直线平行.
___________________________________
(3)如果,垂足为O,
那么.
___________________________________
课堂探究
探究一 命题的概念
观察下面几句话,回答问题
(1)我是初一的学生
(2)对顶角相等
(3)请把窗户关上
(4)等式两边加上相同的数,结果仍是等式.
(5) 画∠AOB=300
(6) 两条直线相交有几个交点?
上面几句话中,是对某件事情做出判断的语句有_____________.
结论:
1.像这样_______一件事情的语句,叫做_______,正确的命题称为_______命题,错误的命题称为_______命题。
2.命题常可以写成“如果......那么......”的形式.“如果”后接的部分是________,“那么” 后接的部分是_________ .
探究二 定理的概念
判断下列语句是否是命题,并指出是真命题还是假命题
(1)同角的余角相等 ;
(2)不许大声说话;
(3)连接A、B两点;
(4)两点之间,线段最短;
(5)等式两边加上相同的数,结果仍是等式;
(6)对顶角不相等.
命题是:__________________________;
真命题是:________________________;
假命题是:________________________ .
结论:
定理是从公理或其他真命题出发,用逻辑推理的方法判断得到的____________.
探究三 证明
已知:如图AB⊥BC,BC⊥CD且∠1=∠2,
求证:BE∥CF
证明:
∵AB⊥BC,BC⊥CD(已知)
∴ = =90°
( )
∵∠1=∠2(已知)
∴ = (等式性质)
∴BE∥CF
( )
结论:
一个命题的正确性需要经过推理才能作出判断,这个推理过程叫作_______.
注意:
证明中的每一步推理都要有根据,不能“想当然”.这些根据,可以是__________也可以是学过的__________、__________、__________等.
重点题型
题型一 判断语句是否命题
1.判断下列语句是不是命题
(1)延长线段AB ( )
(2)两条直线相交,只有一交点 ( )
(3)画线段AB的中点 ( )
(4)若|x|=2,则x=2 ( )
(5)角平分线是一条射线 ( )
题型二 找出命题的题设与结论
2.指出下列命题的题设和结论:
(1)如果同旁内角互补,那么两直线平行.
题设是__________________________________
结论是__________________________________
(2)若a≠b,则a2≠b2.
题设是____________,
结论是_______________
3. 把下列命题改写成"如果…那么…"的形式:
(1)互补的两个角不可能都是锐角;
(2)垂直于同一条直线的两条直线平行;
(3)对顶角相等.
课堂训练
1.下列命题中,正确的个数是( )
①相等的角是对顶角;
②如果两个三角形的底边不同,高也不同,那么这两个三角形的面积不等;
③两条直线相交,只有一个交点;
④凡直角都相等;
⑤凡锐角都相等.
A.1个 B.2个 C.3个 D.5个
2.“等角的补角相等”的题设是 ,结论是 .
3.“一个平面内的两条直线必将这个平面分成四个部分”,该命题是______命题.
4.把下列命题改写成“如果……,那么……”的形式:
(1)平行于同一直线的两条直线平行.
(2)同角的余角相等.
(3)绝对值相等的两个数一定相等.
5.如图,已知直线a、b被直线c所截,在括号内为下面各小题的推理填上适当的根据:
(1)∵a∥b,
∴∠1=∠3
(_________________);
(2)∵∠1=∠3,
∴a∥b (_______________________ );
(3)∵a∥b,
∴∠1=∠2 (________________________);
(4)∵a∥b,
∴∠1+∠4=180 (______________________)
(5)∵∠1=∠2,
∴a∥b (_____________________);
(6)∵∠1+∠4=180 ,
∴a∥b (_____________________).
拓展提升
已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE.
证明:
∵AB∥CD(已知)
∴∠4=∠
( )
∵∠3=∠4(已知)
∴∠3=∠
( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF
( )
即:∠ =∠
∴∠3=∠
( )
∴AD∥BE
( )
第五章 相交线与平行线
5.4 平移
学习目标
1.了解平移的概念,会进行点的平移;
2.理解平移的性质,能解决简单的平移问题.
自主预习
1.下列哪个图形是由左图平移得到的 ( )
2.下列四组图形中,有一组中的两个图形经过平移其中一个能得到 另一个,这组图形是( )
课堂探究
探究一 平移的概念
如何在一张半透明的纸上,画出一排形状和大小如下图的雪人?
图(4)
分析:
可以把一张半透明的纸盖在图(5)上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三……
思考:
在所画出的相邻两个雪人中,找出三组对应点(例如,它们的鼻尖A与A′,帽顶B与B′,纽扣C与C′),连接这些对应点,观察得出的线段,它们的位置、长短有什么关系?
图(5)
可以发现:
AA′∥BB′∥CC′,并且AA′=BB′=CC′
归纳:
(1)把一个图形整体沿_______移动,会得到一个新的图形.新图形与原图形的形状和大小 _________.
(2) 新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点就是_______.连接各组对应点的线段_________.
(3)图形的这种移动,叫做____________.
探究二 平移引申
平移在我们日常生活中是很常见的,利用平移我们也可以做很多美丽的图案,认真观察下图
.
图(6)
归纳:
图形的平移不一定是水平的,也不一定是竖直的.
重点题型
题型 平移三角形
如下图,平移三角形ABC,使点A移动到A′,画出平移后的三角形A′B′C′
随堂训练
1.(2012甘肃白银)将如图所示的图案通过平移后可以得到的图案是( )
( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
2.(2012江西省)如图,有a、b、c三户家用电路接入电表,相邻电路的电线等距排列,则三户所用电线( )
( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
A.a户最长 B.b户最长
C.c户最长 D.三户一样长
3.(2012·浙江义乌)如图所示,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.6 B.8 C.10 D.12
能力提升
三角形ABC在网格中如图所示,请根据下列提示作图
(1)向上平移2个单位长度.
(2)再向右移3个单位长度.
中考链接
1.(2012·福建莆田中考)如图,△A’B’C’是由 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )ABC沿射线AC方向平移2 cm得到,若AC=3cm,则A’C= cm.
( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
2.(2012·湖北宜昌中考)如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )
( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
A.先把△ABC向左平移5个单位,再向下平移2个单位
B.先把△ABC向右平移5个单位,再向下平移2个单位
C.先把△ABC向左平移5个单位,再向上平移2个单位
D.先把△ABC向右平移5个单位,再向上平移2个单位
A
D
B
C
1
2
C
A
B
D
E
F
1
2
A
D
B
C
E
F
1
2
3
4
B′
B
A
C
A′
C′
A
B
C
D
E
F
PAGE
