5.2.2 同角三角函数的基本关系 课件(共25张PPT)
文档属性
| 名称 | 5.2.2 同角三角函数的基本关系 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 00:00:00 | ||
图片预览






文档简介
5.2 三角函数的概念
5.2.2 同角三角函数的基本关系
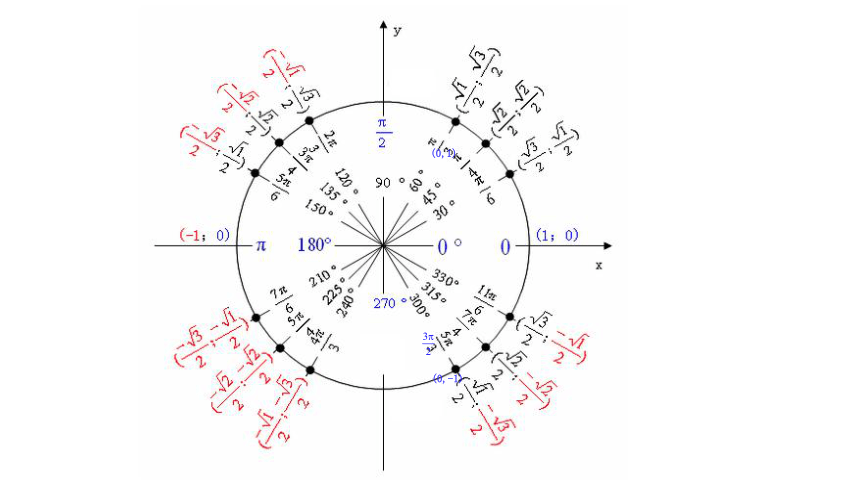
填一填
(0,1)
(0,-1)
新知探索
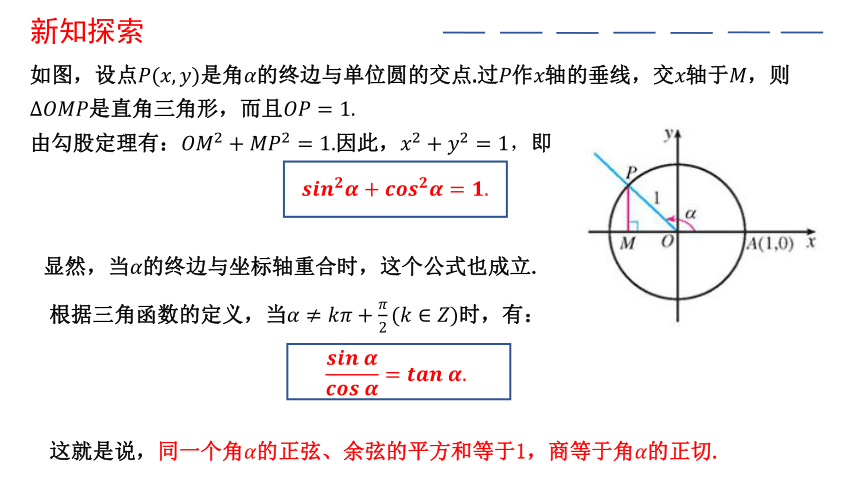
如图,设点????(????,????)是角????的终边与单位圆的交点.过????作????轴的垂线,交????轴于????,则?????????????是直角三角形,而且????????=1.
由勾股定理有:????????2+????????2=1.因此,????2+????2=1,即
?
显然,当????的终边与坐标轴重合时,这个公式也成立.
?
根据三角函数的定义,当????≠????????+????2(????∈????)时,有:
?
????????????????????+????????????????????=????.
?
??????????????????????????????????=?????????????????.
?
这就是说,同一个角????的正弦、余弦的平方和等于1,商等于角????的正切.
?
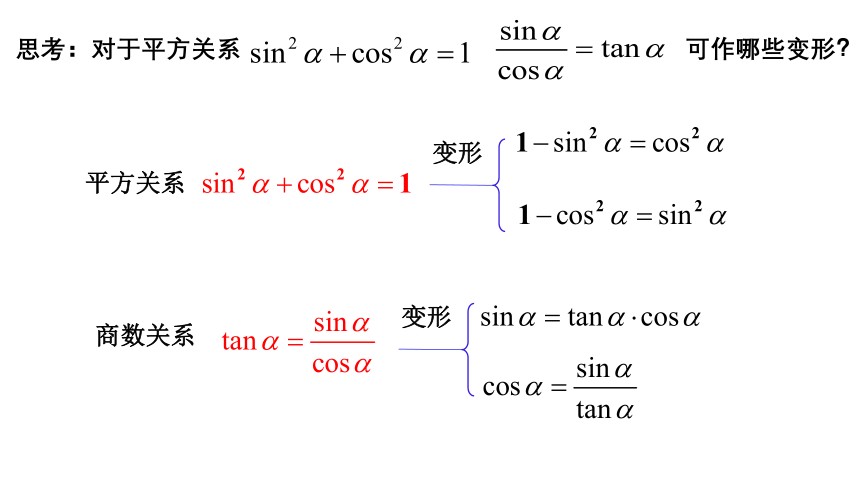
平方关系
商数关系
同一个角的正弦、余弦的平方和等于1,商等于这个角的正切.
同角三角函数的基本关系
思考:“同角”一词的含义是什么?
(1)注意“同角”,这里“同角”有两层含义,一是“角相同”,二是对“任意”一个角(在使函数有意义的前提下)关系式都成立,即与角的表达形式无关,如sin23α+cos23α=1成立,但是sin2α+cos2β=1就不一定成立.
(2)注意同角三角函数的基本关系式都是对于使它们有意义的角而言的,sin2α+cos2α=1对一切α∈R恒成立,而tan α=仅对α≠????????+kπ(k∈Z)成立.
?
?
辨析1:判断正误.
(1)对任意角????,????????????23????+????????????23????=1都成立.( )
(2)对任意角????,?????????????????2?????????????????2=?????????????????2都成立.( )
(3)因为????????????29????4+????????????29????4=1,所以????????????2????+????????????2????=1成立,其中????、????为任意角.( )
(4)对任意角????,?????????????????=???????????????????????????????????都成立.( )
?
√
×
×
×
平方关系
商数关系
变形
变形
思考:对于平方关系 可作哪些变形?
题型一 三角函数求值
2.已知角α的正切求关于sinα,cosα的齐次式的值的方法
(1)关于sinα,cosα的齐次式就是式子中的每一项都是关于sinα,cosα的式子且它们的次数之和相同,设为n次,将分子、分母同除以cosα的n次幂,其式子可化为关于tanα的式子,再代入求值.
(2)若无分母时,把分母看作1,并将1用sin2α+cos2α来代换,将分子、分母同除以cos2α,可化为关于tanα的式子,再代入求值.
题型二 sinα±cosα与sinαcosα关系的应用
三角函数求值中常见的变形公式
(1)sinα+cosα,sinαcosα,sinα-cosα三个式子中,已知其中一个,可以求其他两个,即“知一求二”,
它们的关系是:(sinα+cosα)2=1+2sinαcosα;
(sinα-cosα)2=1-2sinαcosα.
(2)求sinα+cosα或sinα-cosα的值,要根据α的范围注意判断它们的符号.
?
题型三 三角函数式的化简与证明
1.利用同角三角函数关系化简的常用方法
(1)化切为弦,减少函数名称,便于约分化简;
(2)对含根号的,应先把被开方式化为完全平方,去掉根号,为防止出错,去掉根号后首先用绝对值符号表示,然后考虑正负;
(3)对含有高次的三角函数式,可借助于因式分解,或构造平方关系,以便于降幂化简.
2.简单的三角恒等式的证明思路
(1)从一边开始,证明它等于另一边;
(2)证明左、右两边等于同一个式子;
(3)逐步寻找等式成立的条件,达到由繁到简.
当sinα>0时,原式=1;
当sinα<0时,原式=-1.
1.同角三角函数的基本关系
平方关系:
商数关系:
课堂小结
3.已知tanα,求sinα,cosα
2.已知sinα(或cosα)求其它
4.注意分象限讨论
课堂小结
作业:
(1)整理本节课的题型;
(2)优化方案P132的练习
5.2.2 同角三角函数的基本关系
填一填
(0,1)
(0,-1)
新知探索
如图,设点????(????,????)是角????的终边与单位圆的交点.过????作????轴的垂线,交????轴于????,则?????????????是直角三角形,而且????????=1.
由勾股定理有:????????2+????????2=1.因此,????2+????2=1,即
?
显然,当????的终边与坐标轴重合时,这个公式也成立.
?
根据三角函数的定义,当????≠????????+????2(????∈????)时,有:
?
????????????????????+????????????????????=????.
?
??????????????????????????????????=?????????????????.
?
这就是说,同一个角????的正弦、余弦的平方和等于1,商等于角????的正切.
?
平方关系
商数关系
同一个角的正弦、余弦的平方和等于1,商等于这个角的正切.
同角三角函数的基本关系
思考:“同角”一词的含义是什么?
(1)注意“同角”,这里“同角”有两层含义,一是“角相同”,二是对“任意”一个角(在使函数有意义的前提下)关系式都成立,即与角的表达形式无关,如sin23α+cos23α=1成立,但是sin2α+cos2β=1就不一定成立.
(2)注意同角三角函数的基本关系式都是对于使它们有意义的角而言的,sin2α+cos2α=1对一切α∈R恒成立,而tan α=仅对α≠????????+kπ(k∈Z)成立.
?
?
辨析1:判断正误.
(1)对任意角????,????????????23????+????????????23????=1都成立.( )
(2)对任意角????,?????????????????2?????????????????2=?????????????????2都成立.( )
(3)因为????????????29????4+????????????29????4=1,所以????????????2????+????????????2????=1成立,其中????、????为任意角.( )
(4)对任意角????,?????????????????=???????????????????????????????????都成立.( )
?
√
×
×
×
平方关系
商数关系
变形
变形
思考:对于平方关系 可作哪些变形?
题型一 三角函数求值
2.已知角α的正切求关于sinα,cosα的齐次式的值的方法
(1)关于sinα,cosα的齐次式就是式子中的每一项都是关于sinα,cosα的式子且它们的次数之和相同,设为n次,将分子、分母同除以cosα的n次幂,其式子可化为关于tanα的式子,再代入求值.
(2)若无分母时,把分母看作1,并将1用sin2α+cos2α来代换,将分子、分母同除以cos2α,可化为关于tanα的式子,再代入求值.
题型二 sinα±cosα与sinαcosα关系的应用
三角函数求值中常见的变形公式
(1)sinα+cosα,sinαcosα,sinα-cosα三个式子中,已知其中一个,可以求其他两个,即“知一求二”,
它们的关系是:(sinα+cosα)2=1+2sinαcosα;
(sinα-cosα)2=1-2sinαcosα.
(2)求sinα+cosα或sinα-cosα的值,要根据α的范围注意判断它们的符号.
?
题型三 三角函数式的化简与证明
1.利用同角三角函数关系化简的常用方法
(1)化切为弦,减少函数名称,便于约分化简;
(2)对含根号的,应先把被开方式化为完全平方,去掉根号,为防止出错,去掉根号后首先用绝对值符号表示,然后考虑正负;
(3)对含有高次的三角函数式,可借助于因式分解,或构造平方关系,以便于降幂化简.
2.简单的三角恒等式的证明思路
(1)从一边开始,证明它等于另一边;
(2)证明左、右两边等于同一个式子;
(3)逐步寻找等式成立的条件,达到由繁到简.
当sinα>0时,原式=1;
当sinα<0时,原式=-1.
1.同角三角函数的基本关系
平方关系:
商数关系:
课堂小结
3.已知tanα,求sinα,cosα
2.已知sinα(或cosα)求其它
4.注意分象限讨论
课堂小结
作业:
(1)整理本节课的题型;
(2)优化方案P132的练习
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
