17.1 勾股定理(知识讲解)同步学案(含解析)
文档属性
| 名称 | 17.1 勾股定理(知识讲解)同步学案(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-16 16:47:52 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十七章 勾股定理
17.1勾股定理
【学习目标 】:
1. 掌握勾股定理的内容及证明方法,能够熟练地运用勾股定理由已知直角三角形中的两条边长求出第三条边长.
2. 掌握勾股定理,能够运用勾股定理解决简单的实际问题,会运用方程思想解决问题.
3. 熟练应用勾股定理解决直角三角形中的问题,进一步运用方程思想解决问题.
【知识讲解 】:
17.1.1、勾股定理
1、定义:直角三角形两直角边的平方和等于斜边的平方.如果直角三角形的两直角边长分别为,斜边长为,那么.
在我国又称商高定理,在外国则叫毕达哥拉斯定理,或百牛定理.
2、要点诠释:
(1)勾股定理揭示了一个直角三角形三边之间的数量关系.
(2)利用勾股定理,当设定一条直角边长为未知数后,根据题目已知的线段长可以建立方程求解,这样就将数与形有机地结合起来,达到了解决问题的目的.
(3)理解勾股定理的一些变式: ,,
【注意】在勾股定理中,不一定是斜边,不一定是直角,只是习惯写法,做题时应注意题目条件。
17.1.2、勾股定理的证明
【方法一】:将四个全等的直角三角形拼成如图(1)所示的正方形.
【方法二】:将四个全等的直角三角形拼成如图(2)所示的正方形.
【方法三】:如图(3)所示,将两个直角三角形拼成直角梯形.
【典例】在△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为、、.
(1)若=5,=12,求;
(2)若=26,=24,求.
【解答】
解:(1)由勾股定理得
(2)由勾股定理得
【练习1】在△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为、、.
(1)已知=3,=2,求;
(2)已知=17,=8,求。
【练习2】在Rt△ABC中, ∠C=90°。
(1)若 ,,求;
(2)若,∠A=30°,求,。
【练习3】在Rt△ABC中,AB=4,AC=3,求BC的长。
【练习4】已知∠ACB=90°,CD⊥AB,AC=3,BC=4,求CD的长。
【练习5】如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=1,求△ABC的周长.
【练习6】如图所示,如果大正方形的面积是13,小正方形的面积为1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2的值为( )
A.13 B.19 C.25 D.169
17.1.3、三角形中的勾股定理
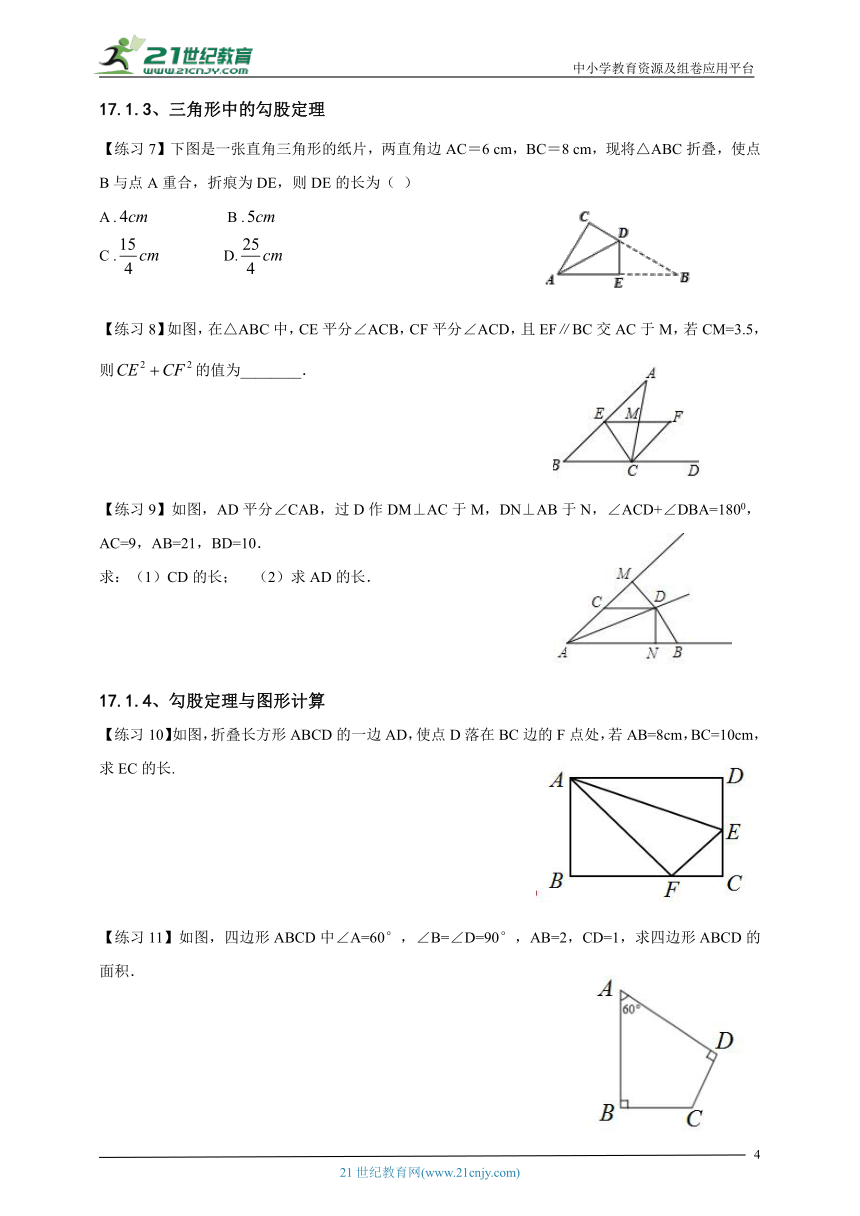
【练习7】下图是一张直角三角形的纸片,两直角边AC=6 cm,BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则DE的长为( )
A . B .
C . D.
【练习8】如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=3.5,则的值为________.
【练习9】如图,AD平分∠CAB,过D作DM⊥AC于M,DN⊥AB于N,∠ACD+∠DBA=1800,AC=9,AB=21,BD=10.
求:(1)CD的长; (2)求AD的长.
17.1.4、勾股定理与图形计算
【练习10】如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
【练习11】如图,四边形ABCD中∠A=60°,∠B=∠D=90°,AB=2,CD=1,求四边形ABCD的面积.
17.1.5、利用勾股定理画长度为无理数的线段
构造直角三角形,两直角边是有理数,斜边长为无理数,利用勾股定理,可以做出长为(n为正整数)的线段,进而在数轴上可画出表示(n是正整数)的点。
易错点:线段的起点不是原点的时候。
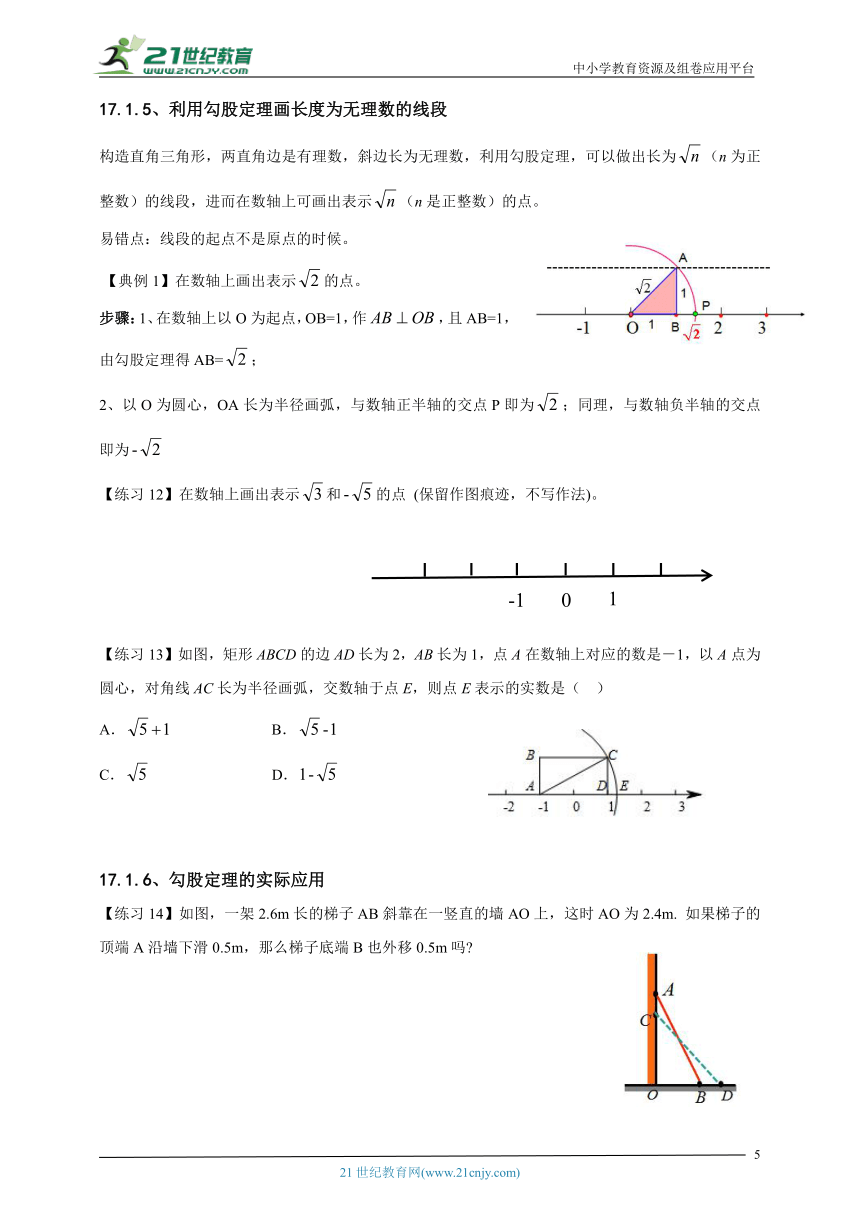
【典例1】在数轴上画出表示的点。
步骤:1、在数轴上以O为起点,OB=1,作,且AB=1,由勾股定理得AB=;
2、以O为圆心,OA长为半径画弧,与数轴正半轴的交点P即为;同理,与数轴负半轴的交点即为
【练习12】在数轴上画出表示和的点 (保留作图痕迹,不写作法)。
【练习13】如图,矩形ABCD的边AD长为2,AB长为1,点A在数轴上对应的数是-1,以A点为圆心,对角线AC长为半径画弧,交数轴于点E,则点E表示的实数是( )
B.
C. D.
17.1.6、勾股定理的实际应用
【练习14】如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m. 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
【练习15】如图,有一段楼梯AC长为15米,由于这段楼梯较陡,为了方便行人通行,现准备新修一条楼梯AD.已知AD=20米,CD=7米,则楼梯的高度AB为 米.
17.1.7、利用勾股定理求最短路径
最短路径问题求解思路:
(1)确定该路径的起点终点;
(2)画出立方体的平面展开图,将立体问题转化为平面问题;
(3)借助勾股定理求得路径的长度;
(4)若展开方法有多种,需比较出最小值,此值为最短路径.
【练习16】如图,有一圆柱,它的高等于8cm,底面直径等于4cm(π=3),在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A相对的B点处的食物,需要爬行的最短路程大约( )
A.10cm B.12cm
C.19cm D.20cm
【练习17】如图,长方体的长、宽、高分别是4,3,5,现有绳子从A出发,沿长方形表面到达C处,问绳子最短是 .
【练习18】如图,圆柱形玻璃杯,高为12 cm,底面周长为18 cm,在杯内离杯底4 cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4 cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 cm。
【练习19】如图,一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近,最短的路程是多少?已知长方体的长2cm、宽为1cm、高为4cm.
参考答案
【练习1】
【答案】(1) (2)15
【解析】(1)由勾股定理得
(2)由勾股定理得
【练习2】
【答案】(1) (2)
【解析】(1)设,由勾股定理得
即,解得,
(2),
设,由勾股定理得
即,解得,
【练习3】
【答案】5或
【解析】(1)当AB为斜边时,由勾股定理得
(2)当BC为斜边时,由勾股定理得
【练习4】
【答案】
【解析】,
由勾股定理得
根据三角形面积公式得
即,
【练习5】
【答案】
【解析】∵AD⊥BC,∴∠ADB=∠ADC=90°.
在Rt△ADB中,∵∠B+∠BAD=90°,∠B=45°,
∴∠B=∠BAD=45°,
∴BD=AD=1,∴AB=.
在Rt△ADC中,∵∠C=30°,
∴AC=2AD=2,
∴CD=,∴BC=BD+CD=,
∴△ABC的周长=AB+AC+BC=.
【练习6】
【答案】C
【解析】根据题意得:,,即,
则,故选C
【练习7】
【答案】D
【解析】
∵△ABC沿DE折叠,使点A与点B重合,
∴EA=EB,AD=BD,
∵∠C=90°,AC=6,BC=8,
∴CD=CB-BD=8-BD,
在Rt△BCE中,
∵AD2=AC2+CD2=62+(8-BD)2,AD=BD,
∴AD=, 在Rt△ADE中,AD2=AE2+DE2,解得DE= 。
故选C
【练习8】
【答案】49
【解析】
∵CE平分∠ACB交AB于E,CF平分∠ACD,
∴∠1=∠2=∠ACB,∠3=∠4=∠ACD,
∴∠2+∠3=(∠ACB+∠ACD)=90°,
∴△CEF是直角三角形,
∵EF∥BC,
∴∠1=∠5,∠4=∠F,
∴∠2=∠5,∠3=∠F,
∴EM=CM,CM=MF,
∵CM=3.5,
∴EF=3.5+3.5=7,
在Rt△CEF中,CE2+CF2=EF2=72=49.
【练习9】
【答案】(1)CD=10 (2)AD=17
【解析】
(1)∵AD平分∠CAB,DM⊥AC,DN⊥AB,
∴DM=DN,AM=AN,
∵∠ACD+∠DCM=180°,∠ACD+∠DBA=180°,
∴∠DCM=∠DBA,
在△DCM和△DBN中,
∵DM=DN,∠DCM=∠DBN,∠DMC=∠DNB,
∴△DCM≌△DBN,
∴CD=BD=10;
(2)∵△DCM≌△DBN,
∴CM=BN,
∵9+CM=21﹣BN,
∴CM=BN=6,
又CD=10,
∴DM==8,
∴AD==17.
【练习10】
【答案】3cm
【解析】设CE=,则DE=(8-).
在Rt△ABF中,由勾股定理,得BF=6.
∴ FC=10-6=4().
在Rt△EFC中,由勾股定理,得,
即.
解得.
即EC的长为3.
【练习11】
解:延长AD、BC相交于点E
∵ ∠B=90°,∠A=45°
∴ ∠E=45°,
∴ AB=BE=2
∵ ∠ADC=90°,
∴ ∠DCE=45°,
∴ CD=DE=1
∴ ,.
∴ .
【练习12】
【答案】
【解析】由勾股定理得,正方形对角线为,则点A表示的数为.
【练习13】
【答案】B
【解析】解:∵AD长为2,AB长为1,∴AC=,
∵A点表示 1,∴E点表示的数为:,故选:B.
【练习14】
【解】:在Rt△AOB中,根据勾股定理得:
∴OB=1
在Rt△COD中,根据勾股定理得
∴梯子的顶端沿墙下滑0.5m时,梯子底端并不是也外移0.5m,而是外移约0.77m.
【练习15】
【答案】12
【解析】解:设BC=x,
则在Rt△ACB和Rt△ADB中,
AB2=AD2﹣BD2,AB2=AC2﹣BC2,
故202﹣(7+BC)2=152﹣BC2,
解得:BC=9,
∴AB2=152﹣92=144,
∴AB=12.
【练习16】
【答案】A
【解析】展开圆柱的半个侧面,得到一个矩形:矩形的长是圆柱底面周长的一半即2π=6,矩形的宽是圆柱的高即8.根据勾股定理得:蚂蚁爬行的最短路程即展开矩形的对角线长即10.故选A.
【练习17】
【答案】
【解析】
解:如图所示,将长方体右边的表面翻折90°(展开),连接AC,
显然两点之间线段最短,AC为点A到点C的最短距离,
由勾股定理知:AC2=52+(4+3)2=74,
AC=.即绳子最短为.
故答案为:.
【练习18】
【答案】15
【解析】如图:
圆柱形玻璃杯展开(沿点A竖直剖开)后侧面是一个长18宽12的矩形,作点A关于杯上沿MN的对称点B,连接BC交MN于点P,连接BM,过点C作AB的垂线交剖开线MA于点D。
由轴对称的性质和三角形三边关系知AP+PC为蚂蚁到达蜂蜜的最短距离,且AP=BP。
由已知和矩形的性质,得DC=9,BD=12。
在Rt△BCD中,由勾股定理得。
∴AP+PC=BP+PC=BC=15,
即蚂蚁到达蜂蜜的最短距离为15cm。
【练习19】
【答案】解:如图:根据题意,如上图所示,最短路径有以下三种情况:
(1)沿AA′,A′C′,C′B′,B′B剪开,得图(1)AB′2=AB2+BB′2=(2+1)2+42=25;
(2)沿AC,CC′,C′B′,B′D′,D′A′,A′A剪开,得图(2)AB′2=AC2+B′C2=22+(4+1)2=4+25=29;(3)沿AD,DD′,B′D′,C′B′,C′A′,AA′剪开,得图(3)AB′2=AD2+B′D2=12+(4+2)2=1+36=37;综上所述,最短路径应为(1)所示,所以AB′2=25,即AB′=5cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十七章 勾股定理
17.1勾股定理
【学习目标 】:
1. 掌握勾股定理的内容及证明方法,能够熟练地运用勾股定理由已知直角三角形中的两条边长求出第三条边长.
2. 掌握勾股定理,能够运用勾股定理解决简单的实际问题,会运用方程思想解决问题.
3. 熟练应用勾股定理解决直角三角形中的问题,进一步运用方程思想解决问题.
【知识讲解 】:
17.1.1、勾股定理
1、定义:直角三角形两直角边的平方和等于斜边的平方.如果直角三角形的两直角边长分别为,斜边长为,那么.
在我国又称商高定理,在外国则叫毕达哥拉斯定理,或百牛定理.
2、要点诠释:
(1)勾股定理揭示了一个直角三角形三边之间的数量关系.
(2)利用勾股定理,当设定一条直角边长为未知数后,根据题目已知的线段长可以建立方程求解,这样就将数与形有机地结合起来,达到了解决问题的目的.
(3)理解勾股定理的一些变式: ,,
【注意】在勾股定理中,不一定是斜边,不一定是直角,只是习惯写法,做题时应注意题目条件。
17.1.2、勾股定理的证明
【方法一】:将四个全等的直角三角形拼成如图(1)所示的正方形.
【方法二】:将四个全等的直角三角形拼成如图(2)所示的正方形.
【方法三】:如图(3)所示,将两个直角三角形拼成直角梯形.
【典例】在△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为、、.
(1)若=5,=12,求;
(2)若=26,=24,求.
【解答】
解:(1)由勾股定理得
(2)由勾股定理得
【练习1】在△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为、、.
(1)已知=3,=2,求;
(2)已知=17,=8,求。
【练习2】在Rt△ABC中, ∠C=90°。
(1)若 ,,求;
(2)若,∠A=30°,求,。
【练习3】在Rt△ABC中,AB=4,AC=3,求BC的长。
【练习4】已知∠ACB=90°,CD⊥AB,AC=3,BC=4,求CD的长。
【练习5】如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=1,求△ABC的周长.
【练习6】如图所示,如果大正方形的面积是13,小正方形的面积为1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2的值为( )
A.13 B.19 C.25 D.169
17.1.3、三角形中的勾股定理
【练习7】下图是一张直角三角形的纸片,两直角边AC=6 cm,BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则DE的长为( )
A . B .
C . D.
【练习8】如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=3.5,则的值为________.
【练习9】如图,AD平分∠CAB,过D作DM⊥AC于M,DN⊥AB于N,∠ACD+∠DBA=1800,AC=9,AB=21,BD=10.
求:(1)CD的长; (2)求AD的长.
17.1.4、勾股定理与图形计算
【练习10】如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
【练习11】如图,四边形ABCD中∠A=60°,∠B=∠D=90°,AB=2,CD=1,求四边形ABCD的面积.
17.1.5、利用勾股定理画长度为无理数的线段
构造直角三角形,两直角边是有理数,斜边长为无理数,利用勾股定理,可以做出长为(n为正整数)的线段,进而在数轴上可画出表示(n是正整数)的点。
易错点:线段的起点不是原点的时候。
【典例1】在数轴上画出表示的点。
步骤:1、在数轴上以O为起点,OB=1,作,且AB=1,由勾股定理得AB=;
2、以O为圆心,OA长为半径画弧,与数轴正半轴的交点P即为;同理,与数轴负半轴的交点即为
【练习12】在数轴上画出表示和的点 (保留作图痕迹,不写作法)。
【练习13】如图,矩形ABCD的边AD长为2,AB长为1,点A在数轴上对应的数是-1,以A点为圆心,对角线AC长为半径画弧,交数轴于点E,则点E表示的实数是( )
B.
C. D.
17.1.6、勾股定理的实际应用
【练习14】如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m. 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
【练习15】如图,有一段楼梯AC长为15米,由于这段楼梯较陡,为了方便行人通行,现准备新修一条楼梯AD.已知AD=20米,CD=7米,则楼梯的高度AB为 米.
17.1.7、利用勾股定理求最短路径
最短路径问题求解思路:
(1)确定该路径的起点终点;
(2)画出立方体的平面展开图,将立体问题转化为平面问题;
(3)借助勾股定理求得路径的长度;
(4)若展开方法有多种,需比较出最小值,此值为最短路径.
【练习16】如图,有一圆柱,它的高等于8cm,底面直径等于4cm(π=3),在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A相对的B点处的食物,需要爬行的最短路程大约( )
A.10cm B.12cm
C.19cm D.20cm
【练习17】如图,长方体的长、宽、高分别是4,3,5,现有绳子从A出发,沿长方形表面到达C处,问绳子最短是 .
【练习18】如图,圆柱形玻璃杯,高为12 cm,底面周长为18 cm,在杯内离杯底4 cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4 cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 cm。
【练习19】如图,一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近,最短的路程是多少?已知长方体的长2cm、宽为1cm、高为4cm.
参考答案
【练习1】
【答案】(1) (2)15
【解析】(1)由勾股定理得
(2)由勾股定理得
【练习2】
【答案】(1) (2)
【解析】(1)设,由勾股定理得
即,解得,
(2),
设,由勾股定理得
即,解得,
【练习3】
【答案】5或
【解析】(1)当AB为斜边时,由勾股定理得
(2)当BC为斜边时,由勾股定理得
【练习4】
【答案】
【解析】,
由勾股定理得
根据三角形面积公式得
即,
【练习5】
【答案】
【解析】∵AD⊥BC,∴∠ADB=∠ADC=90°.
在Rt△ADB中,∵∠B+∠BAD=90°,∠B=45°,
∴∠B=∠BAD=45°,
∴BD=AD=1,∴AB=.
在Rt△ADC中,∵∠C=30°,
∴AC=2AD=2,
∴CD=,∴BC=BD+CD=,
∴△ABC的周长=AB+AC+BC=.
【练习6】
【答案】C
【解析】根据题意得:,,即,
则,故选C
【练习7】
【答案】D
【解析】
∵△ABC沿DE折叠,使点A与点B重合,
∴EA=EB,AD=BD,
∵∠C=90°,AC=6,BC=8,
∴CD=CB-BD=8-BD,
在Rt△BCE中,
∵AD2=AC2+CD2=62+(8-BD)2,AD=BD,
∴AD=, 在Rt△ADE中,AD2=AE2+DE2,解得DE= 。
故选C
【练习8】
【答案】49
【解析】
∵CE平分∠ACB交AB于E,CF平分∠ACD,
∴∠1=∠2=∠ACB,∠3=∠4=∠ACD,
∴∠2+∠3=(∠ACB+∠ACD)=90°,
∴△CEF是直角三角形,
∵EF∥BC,
∴∠1=∠5,∠4=∠F,
∴∠2=∠5,∠3=∠F,
∴EM=CM,CM=MF,
∵CM=3.5,
∴EF=3.5+3.5=7,
在Rt△CEF中,CE2+CF2=EF2=72=49.
【练习9】
【答案】(1)CD=10 (2)AD=17
【解析】
(1)∵AD平分∠CAB,DM⊥AC,DN⊥AB,
∴DM=DN,AM=AN,
∵∠ACD+∠DCM=180°,∠ACD+∠DBA=180°,
∴∠DCM=∠DBA,
在△DCM和△DBN中,
∵DM=DN,∠DCM=∠DBN,∠DMC=∠DNB,
∴△DCM≌△DBN,
∴CD=BD=10;
(2)∵△DCM≌△DBN,
∴CM=BN,
∵9+CM=21﹣BN,
∴CM=BN=6,
又CD=10,
∴DM==8,
∴AD==17.
【练习10】
【答案】3cm
【解析】设CE=,则DE=(8-).
在Rt△ABF中,由勾股定理,得BF=6.
∴ FC=10-6=4().
在Rt△EFC中,由勾股定理,得,
即.
解得.
即EC的长为3.
【练习11】
解:延长AD、BC相交于点E
∵ ∠B=90°,∠A=45°
∴ ∠E=45°,
∴ AB=BE=2
∵ ∠ADC=90°,
∴ ∠DCE=45°,
∴ CD=DE=1
∴ ,.
∴ .
【练习12】
【答案】
【解析】由勾股定理得,正方形对角线为,则点A表示的数为.
【练习13】
【答案】B
【解析】解:∵AD长为2,AB长为1,∴AC=,
∵A点表示 1,∴E点表示的数为:,故选:B.
【练习14】
【解】:在Rt△AOB中,根据勾股定理得:
∴OB=1
在Rt△COD中,根据勾股定理得
∴梯子的顶端沿墙下滑0.5m时,梯子底端并不是也外移0.5m,而是外移约0.77m.
【练习15】
【答案】12
【解析】解:设BC=x,
则在Rt△ACB和Rt△ADB中,
AB2=AD2﹣BD2,AB2=AC2﹣BC2,
故202﹣(7+BC)2=152﹣BC2,
解得:BC=9,
∴AB2=152﹣92=144,
∴AB=12.
【练习16】
【答案】A
【解析】展开圆柱的半个侧面,得到一个矩形:矩形的长是圆柱底面周长的一半即2π=6,矩形的宽是圆柱的高即8.根据勾股定理得:蚂蚁爬行的最短路程即展开矩形的对角线长即10.故选A.
【练习17】
【答案】
【解析】
解:如图所示,将长方体右边的表面翻折90°(展开),连接AC,
显然两点之间线段最短,AC为点A到点C的最短距离,
由勾股定理知:AC2=52+(4+3)2=74,
AC=.即绳子最短为.
故答案为:.
【练习18】
【答案】15
【解析】如图:
圆柱形玻璃杯展开(沿点A竖直剖开)后侧面是一个长18宽12的矩形,作点A关于杯上沿MN的对称点B,连接BC交MN于点P,连接BM,过点C作AB的垂线交剖开线MA于点D。
由轴对称的性质和三角形三边关系知AP+PC为蚂蚁到达蜂蜜的最短距离,且AP=BP。
由已知和矩形的性质,得DC=9,BD=12。
在Rt△BCD中,由勾股定理得。
∴AP+PC=BP+PC=BC=15,
即蚂蚁到达蜂蜜的最短距离为15cm。
【练习19】
【答案】解:如图:根据题意,如上图所示,最短路径有以下三种情况:
(1)沿AA′,A′C′,C′B′,B′B剪开,得图(1)AB′2=AB2+BB′2=(2+1)2+42=25;
(2)沿AC,CC′,C′B′,B′D′,D′A′,A′A剪开,得图(2)AB′2=AC2+B′C2=22+(4+1)2=4+25=29;(3)沿AD,DD′,B′D′,C′B′,C′A′,AA′剪开,得图(3)AB′2=AD2+B′D2=12+(4+2)2=1+36=37;综上所述,最短路径应为(1)所示,所以AB′2=25,即AB′=5cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
