17.1 勾股定理(练习巩固)(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
17.1勾股定理(练习巩固)
一、单选题
1.已知一个直角三角形的两边长分别为3和4,则第三边长是( )
A.5 B.25 C. D.5或
2.如图,有两棵树,一棵高5米,另一棵高2米,两树相距5米,一只小鸟从一棵树飞到另一棵树的树梢,至少飞了( )米。
A.米 B.5 米 C.4米 D.米
3.如图,在 中,有一点 在 上移动,若 , ,则 的最小值为( )
A. B. C. D.
4.在△ABC中,AB=AC=5,BC=6,M是BC的中点,MN⊥AC于点N。则MN=( )
A. B. C.6 D.11
5.如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要多米?( )
A.4 B.8 C.9 D.7
6.如图所示,某人到岛上去探宝,从A处登陆后先往北走9km,又往东走6km,再折回向北走3km,往西一拐,仅走1km就找到宝藏 问登陆点A与宝藏埋藏点B之间的距离是 .
A.10 B.11 C.12 D.13
7.下列选项中,不能用来验证勾股定理的是( )
A. B.
C. D.
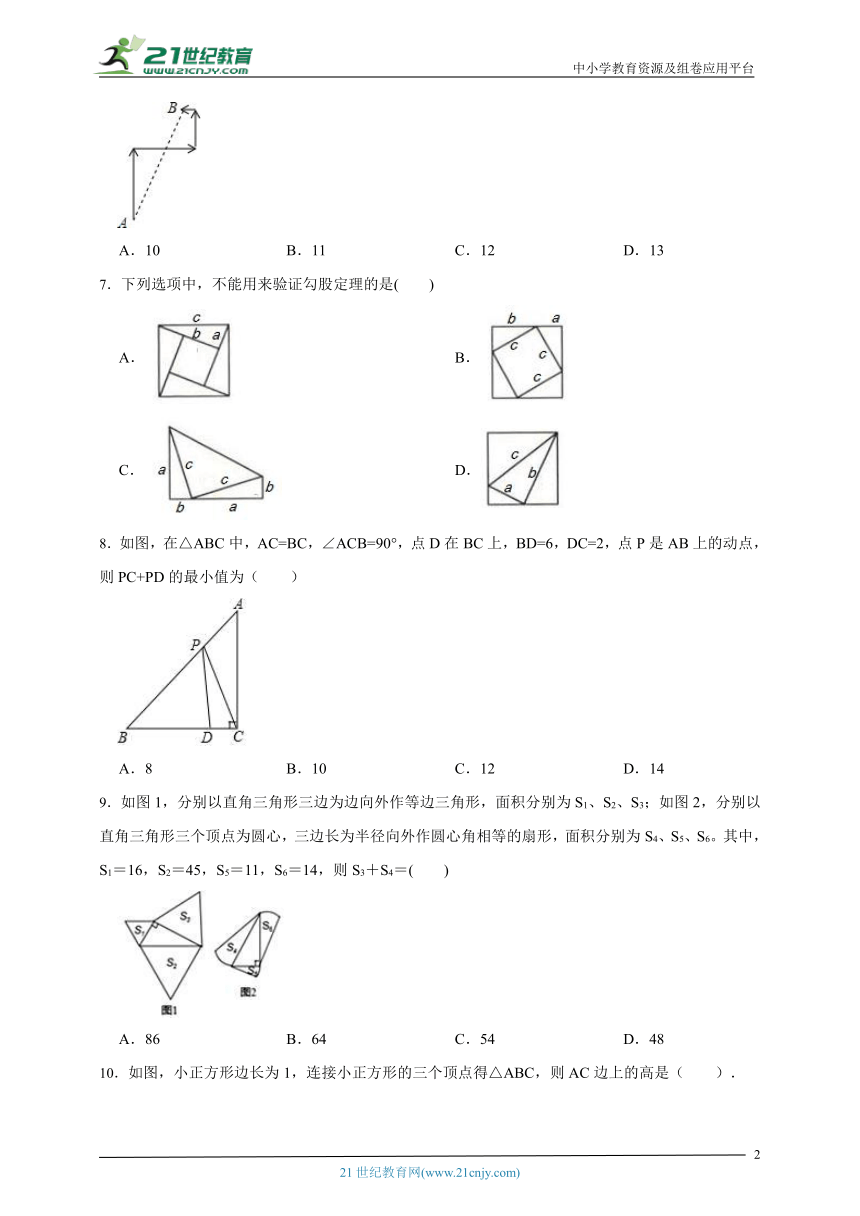
8.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=6,DC=2,点P是AB上的动点,则PC+PD的最小值为( )
A.8 B.10 C.12 D.14
9.如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6。其中,S1=16,S2=45,S5=11,S6=14,则S3+S4=( )
A.86 B.64 C.54 D.48
10.如图,小正方形边长为1,连接小正方形的三个顶点得△ABC,则AC边上的高是( ).
A. B. C. D.
二、填空题
11.设a、b是直角三角形的两条直角边,若该直角三角形的周长为6,斜边长为2.5,则ab的值是 .
12.在中,,,作边上的垂线交于点,交的延长线于点,连接,若刚好, .
13.如图,在△ABC中,AB=AC=10,BC=12,点D是边BC的中点,直线MN是AB的垂直平分线,点E是MN上的一个动点,则△BDE周长的最小值是 .
14.如图,在Rt△ABC中,∠ACB = 90°, ,点D、E分别在边AB上,且AD = 2,∠DCE = 45°,那么DE = .
15.如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成.若较短的直角边BC=2.5,将四个直角三角形中较长的直角边分别向外延长一倍,得到图2所示的“数学风车”,若△BCD的周长是15,则这个风车的外围周长是 .
三、解答题
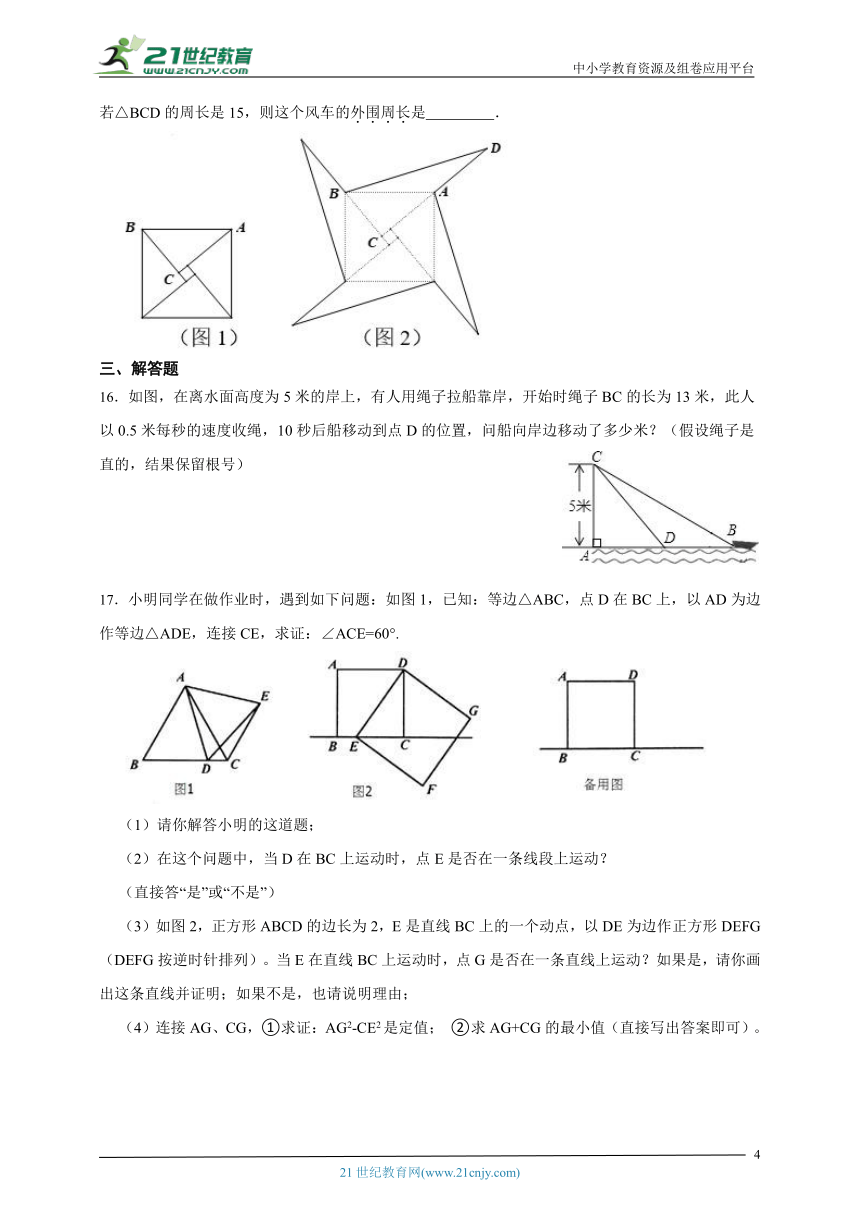
16.如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米每秒的速度收绳,10秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)
17.小明同学在做作业时,遇到如下问题:如图1,已知:等边△ABC,点D在BC上,以AD为边作等边△ADE,连接CE,求证:∠ACE=60°.
(1)请你解答小明的这道题;
(2)在这个问题中,当D在BC上运动时,点E是否在一条线段上运动?
(直接答“是”或“不是”)
(3)如图2,正方形ABCD的边长为2,E是直线BC上的一个动点,以DE为边作正方形DEFG(DEFG按逆时针排列)。当E在直线BC上运动时,点G是否在一条直线上运动?如果是,请你画出这条直线并证明;如果不是,也请说明理由;
(4)连接AG、CG,①求证:AG2-CE2是定值; ②求AG+CG的最小值(直接写出答案即可)。
18.如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
(1)AC的长等于 ;
(2)在线段AC上有一点D,满足AB2=AD AC,请在如图所示的网格中,用无刻度的直尺,画出点D,并简要说明点D的位置是如何找到的(不要求证明).
四、综合题
19.如图,居民楼与马路是平行的,在一楼的点A处测得它到马路的距离为9m,已知在距离载重汽车41m处就可受到噪声影响.
(1)试求在马路上以4m/s速度行驶的载重汽车,能给一楼A处的居民带来多长时间的噪音影响?
(2)若时间超过25秒,则此路禁止该车通行,你认为载重汽车可以在这条路上通行吗?
20.如图,一艘船由A港沿北偏东60°方向航行10km至B港,然后再沿北偏西30°方向航行10km至C港。
(1)求A,C两港之间的距离(结果保留到0.1km,参考数据: ≈1.414, ≈1.732);
(2)确定C港在A港的什么方向。
21.如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=6,CD=4,求:
(1)AB的长;
(2)四边形ABCD的面积.
22.在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(﹣4,6),(﹣1,4).
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC关于x轴对称的△A1B1C1;
(3)请在y轴上求作一点P,使△PB1C的周长最小,并写出点P的坐标.
23.如图1,纸上有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形.
(1)拼成的正方形的面积与边长分别是多少?
(2)如图2所示,以数轴的单位长度的线段为边作一个直角三角形,以数轴的﹣1点为圆心,直角三角形的最大边为半径画弧,交数轴正半轴于点A,那么点A表示的数是多少?点A表示的数的相反数是多少?
(3)如图3你能把十三个小正方形组成的图形纸,剪开并拼成正方形吗?若能,请画出示意图,并求它的边长是多少?
24.如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,点P从点A开始沿A B运动,速度为每秒1cm,点Q从点B开始沿B→C→A运动,速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求PQ的长;
(2)从出发几秒钟后,DPQB第一次能形成等腰三角形?
(3)当点Q在边CA上运动时,直接写出使△BCQ成为等腰三角形的运动时间.
参考答案
1.【答案】D
【解析】直角三角形的边满足勾股定理,已知直角三角形的两边长分别为3和4,则有两种情况,一种是这两边都是直角边;另一种是已知的两边一条是直角边,另一条是斜边.
【解答】当已知边3和4都是直角边,则第三边是斜边,长是;
当已知边3和4一条是直角边一条是斜边时,则第三边是直角边长是:=.
故选D.
2.【答案】A
【解析】勾股定理,如果一个三角形,两边的平方的和等于第三边的平方,则为直角三角形。
【解答】两棵树间的高度差为3米,间距为5米,
根据勾股定理:飞行距离最少是:
故选A.
3.【答案】D
【解析】解:过A作AD⊥BC于D,
∵AB=AC=5,AD⊥BC,
∴BD=BC=3,AD=,
当BP⊥AC时,BP最小=,
∴AP+BP+CP的最小值=AC+BP=5+4.8=9.8。
故答案为:D.
4.【答案】A
【解析】解:如图,连接AM,
∵AB=AC,点M为BC中点,
∴AM⊥CM,BM=CM=BC=3,
在Rt△ABM中,AB=5,BM=3,
∴AM=,
又∵S△AMC=MN AC=AM MC,
∴MN==.
故答案为:A.
5.【答案】D
【解析】解:由勾股定理得:
楼梯的水平宽度= =4,
∵地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
地毯的长度至少是3+4=7米.
故选D.
6.【答案】D
【解析】解:如图,作过点A的东西方向的直线AD,过点B作BC⊥AD于C,
则AC=6-1=5km,BC=9+3=12km,
在Rt△ABC中,由勾股定理求得AB= = =13(km).
所以登陆点A与宝藏埋藏点B之间的距离是13km.
故答案为:D.
7.【答案】D
【解析】解:A、∵大正方形的面积=c2=4×a(a+b)+(b-a)2,∴a2+b2=c2,正确;
B、大正方形的面积=(a+b)2=4×ab+c2,∴a2+b2=c2,正确;
C、梯形的面积=(a+b)(a+b)=2×ab+c2,∴a2+b2=c2,正确;
D、无法确定大正方形的边长,不能利用a、b、c来构造等式,错误;
故答案为:D.
8.【答案】B
【解析】解:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于P,连接CP.
此时DP+CP=DP+PC′=DC′的值最小.
∵DC=2,BD=6,
∴BC=8,
连接BC′,由对称性可知∠C′BA=∠CBA=45°,
∴∠CBC′=90°,
∴BC′⊥BC,∠BCC′=∠BC′C=45°,
∴BC=BC′=8,
根据勾股定理可得DC′= .故答案为:B.
9.【答案】C
【解析】设直角三角形的三边从小到大是a,b,c.在图1,可得 ,又因a2+b2=c2,所以 ;图2中, ,又因a2+b2=c2,所以 ,即可得 ,
故答案为:C.
10.【答案】D
【解析】根据四边形的总面积为4,可得出△ABF=△ACD=1,
△BCE的面积=
△ABC的面积=4-1-1-=,
在Rt△ADC中,AC=,
设AC 边上的高为x,
根据
可解得x=.
故答案为:D.
11.【答案】3
【解析】解:∵a、b是直角三角形的两条直角边,直角三角形的周长为6,斜边长为2.5,
∴a+b=3.5,a2+b2=2.52=6.25,
(a+b)2=12.25,
∴a2+b2+2ab=12.25,
∴2ab=6,
解得:ab=3.
故答案为:3.
12.【答案】
【解析】解:,
,
,
,
,,
∴△ABC≌△EFC(AAS),
,
在中
,
故答案为:.
13.【答案】14
【解析】解:连接AD,AE,
∵MN是AB的垂直平分线,
∴AE=BE,
∵△ABC是等腰三角形,D是BC的中点,
∴AD⊥BC,
∴△BDE的周长=BD+DE+BE=BD+DE+AE≥BD+AD,
当A、E、D三点共线时,△BDE的周长最小,
∵AB=AC=10,BC=12,即BD=6,
∴AD=8,
∴△BDE的周长最小值为BD+AD=6+8=14,
∴△BDE的周长最小值为14,
故答案为:14.
14.【答案】
【解析】解:如图,将△BCE绕点C逆时针旋转90°得到△ACF,连接DF,
∵∠ACB=90°,AC=BC=4 ,
∴AB=8,∠CAB=∠ABC,
∵AD=2,
∴BD=6=DE+BE,
∵将△BCE绕点C逆时针旋转90°得到△ACF
∴△AFC≌△BEC
∴AF=BE,CF=BC,∠FAC=∠ABC=45°=∠CAB,∠ACF=∠BCE,
∴∠FAD=90°
∵∠DCE=45°,∠ACB=90°,
∴∠ACD+∠BCE=45°,
∴∠ACD+∠FCA=45°=∠DCE,且CF=CE,CD=CD,
∴△FCD≌△ECD(SAS)
∴DE=DF,
在Rt△ADF中,DF2=AD2+AF2,
∴DE2=4+(6﹣DE)2,
∴DE= .
故答案为 .
15.【答案】38
【解析】解:设图2中的“数学风车”四个直角三角形的斜边长为x,AC=y,依题可得,
,
解得:,
∴这个风车的外围周长为:4×6.5+4×3=38.
故答案为:38.
16.【答案】解:在Rt△ABC中:
∵∠CAB=90°,BC=13米,AC=5米,
∴AB= =12(米),
∵此人以0.5米每秒的速度收绳,10秒后船移动到点D的位置,
∴CD=13﹣0.5×10=8(米),
∴AD= = = (米),
∴BD=AB﹣AD=12﹣ (米),
答:船向岸边移动了(12﹣ )米
17.【答案】(1)解:证明:∵△ABC和△ADE是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,∠B=60°,
∴∠BAD=∠CAE,∴△ABD △ACE,
∴∠ACE=∠B=60°.
(2)解:是;∵∠ACE=60°,∠ACB=60°,∴∠BCE=120°,
∴E在以CB为一条边的120°角的另一边上,
当点D与B重合,E与C重合;
当点D与C重合时,CE的长最长=AC;
故点E在一条线段上运动。
(3)解:是。证明:过G作GH⊥CD于H,∵四边形ABCD和四边形DEFG是正方形,
∴∠DCE=90°,∠EDG=90°,DE=DG,
∴∠EDC+∠GDC=90°,∠EDC+∠CED=90°,
∴∠GDC=∠CED,又∵DE=DG,∠DCE=∠GHD=90度,
∴△CDE △HGD,∴GH=CD=2.
又∵GH⊥CD,∴点G是在与CD的距离为2的直线上,过G作直线//CD,即点G在直线l上运动。
(4)解:①延长AD交直线l于P,由(1)可得△CDE △HGD,
∴CE=DH。
∵l//CD,GH⊥CD,∴∠DHG=∠PGH=90°,
又∵∠PDH=90°,∴四边形DHGP是矩形,
∴PG=DH=CE,PD=GH=2,
在Rt△AGP中,AG2-PG2=AP2=42=16,
∴AG2-CE2=AG2-PG2=16是定值。
②过A作关于l的对称点A′,连接A′C,交直线l于G′,则AG+CG≥A′G′+CG′=A′C,
在Rt△A′CD中,CD=2,A′D=6,∴A′C = 。
18.【答案】(1)5
(2)
【解析】(1)AC= ;
(2)如图,连接格点M和N,由图可知:
AB=AM=4,
BC=AN= ,
AC=MN= ,
∴△ABC≌△MAN,
∴∠AMN=∠BAC,
∴∠MAD+∠CAB=∠MAD+∠AMN=90°,
∴MN⊥AC,
易解得△MAN以MN为底时的高为 ,
∵AB2=AD AC,
∴AD=AB2÷AC= ,
综上可知,MN与AC的交点即为所求D点.
19.【答案】(1)解:∵由题意得AC=9,AB=AD=41,AC⊥BD,
∴Rt△ACB中,BC= ,
Rt△ACD中,DC= ,
∴BD=80,
∴80÷4=20(s),
∴受影响时间为20s
(2)解:∵20<25,
∴可以通行
20.【答案】(1) 由题意知,∠DAB+∠EBA=180°,
∠ABC=90°
∵AB=CB=10,
∴AC=
蓑衣AC约等于14.1km
(2)∠FCA-∠DAC=60°-45°=15°
21.【答案】(1)解:如图,延长AD,BC交于点E.
在Rt△ABE中,∠A=60°,∴∠E=30°.
在Rt△CDE中,CD=4,∠E=30°.∴CE=2CD=8.
∴BE=BC+CE=6+8=14.
设AB=x,则AE=2x,根据勾股定理得:x2+142=(2x)2,
解得x= ,则AB= 。
(2)解:在Rt△CDE中,∠CDE=90°,
∴DE= = =4 .
∴S四边形ABCD=S△ABE-S△CDE= ·AB·BE- ·CD·DE= × ×14- ×4×4 = .
22.【答案】(1)解:如图所示;
(2)解:如图,即为所求;
(3)解:作点B关于y轴的对称点B2,连接AB2交y轴于点P,则点P即为所求.
设直线AB2的解析式为y=kx+b(k≠0),
∵A(﹣4,6),B2(2,2),
∴ ,解得 ,
∴直线AB2的解析式为:y=﹣ x+ ,
∴当x=0时,y= ,
∴P(0, ).
23.【答案】(1)解:拼成的正方形的面积等于原来5个小正方形面积之和,即为5,
∵正方形的面积等于边长的平方,∴正方形的边长即为面积的算术平方根,为 ;
(2)解:设点A表示的数为x,则由题意可得:x-(-1)= ,∴x= ,
又∵ ,∴点A表示的数是 ,点A表示的数的相反数是 ;
(3)解:如图,
可以按如下方式把十三个小正方形组成的图形纸剪拼成正方形,其中三角形A可以平移至三角形C,三角形B可以平移至三角形D,由题意可知其边长为13的算术平方根,即 .
24.【答案】(1)解:当t=2时,则AP=2,BQ=2t=4,
∵AB=8cm,
∴BP=AB﹣AP=8﹣2=6(cm),
在Rt△BPQ中,由勾股定理可得PQ= (cm),
即PQ的长为2 cm
(2)解:由题意可知AP=t,BQ=2t,
∵AB=8,
∴BP=AB﹣AP=8﹣t,
当△PQB为等腰三角形时,则有BP=BQ,
即8﹣t=2t,
解得t= ,
∴出发 秒后△PQB能形成等腰三角形
(3)解:①当CQ=BQ时(如下图),则∠C=∠CBQ,
∵∠ABC=90°
∴∠CBQ+∠ABQ=90°
∠A+∠C=90°
∴∠A=∠ABQ
∴BQ=AQ
∴CQ=AQ=5
∴BC+CQ=11
∴t=11÷2=5.5秒
②当CQ=BC时(如图2),则BC+CQ=12
∴t=12÷2=6秒
③当BC=BQ时(如图3),过B点作BE⊥AC于点E,
则BE= ,
∴CE= ,
故CQ=2CE=7.2,
所以BC+CQ=13.2,
∴t=13.2÷2=6.6秒
综上:t的值为6.6秒或6秒或5.5秒时,△BCQ为等腰三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
17.1勾股定理(练习巩固)
一、单选题
1.已知一个直角三角形的两边长分别为3和4,则第三边长是( )
A.5 B.25 C. D.5或
2.如图,有两棵树,一棵高5米,另一棵高2米,两树相距5米,一只小鸟从一棵树飞到另一棵树的树梢,至少飞了( )米。
A.米 B.5 米 C.4米 D.米
3.如图,在 中,有一点 在 上移动,若 , ,则 的最小值为( )
A. B. C. D.
4.在△ABC中,AB=AC=5,BC=6,M是BC的中点,MN⊥AC于点N。则MN=( )
A. B. C.6 D.11
5.如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要多米?( )
A.4 B.8 C.9 D.7
6.如图所示,某人到岛上去探宝,从A处登陆后先往北走9km,又往东走6km,再折回向北走3km,往西一拐,仅走1km就找到宝藏 问登陆点A与宝藏埋藏点B之间的距离是 .
A.10 B.11 C.12 D.13
7.下列选项中,不能用来验证勾股定理的是( )
A. B.
C. D.
8.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=6,DC=2,点P是AB上的动点,则PC+PD的最小值为( )
A.8 B.10 C.12 D.14
9.如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6。其中,S1=16,S2=45,S5=11,S6=14,则S3+S4=( )
A.86 B.64 C.54 D.48
10.如图,小正方形边长为1,连接小正方形的三个顶点得△ABC,则AC边上的高是( ).
A. B. C. D.
二、填空题
11.设a、b是直角三角形的两条直角边,若该直角三角形的周长为6,斜边长为2.5,则ab的值是 .
12.在中,,,作边上的垂线交于点,交的延长线于点,连接,若刚好, .
13.如图,在△ABC中,AB=AC=10,BC=12,点D是边BC的中点,直线MN是AB的垂直平分线,点E是MN上的一个动点,则△BDE周长的最小值是 .
14.如图,在Rt△ABC中,∠ACB = 90°, ,点D、E分别在边AB上,且AD = 2,∠DCE = 45°,那么DE = .
15.如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成.若较短的直角边BC=2.5,将四个直角三角形中较长的直角边分别向外延长一倍,得到图2所示的“数学风车”,若△BCD的周长是15,则这个风车的外围周长是 .
三、解答题
16.如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米每秒的速度收绳,10秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)
17.小明同学在做作业时,遇到如下问题:如图1,已知:等边△ABC,点D在BC上,以AD为边作等边△ADE,连接CE,求证:∠ACE=60°.
(1)请你解答小明的这道题;
(2)在这个问题中,当D在BC上运动时,点E是否在一条线段上运动?
(直接答“是”或“不是”)
(3)如图2,正方形ABCD的边长为2,E是直线BC上的一个动点,以DE为边作正方形DEFG(DEFG按逆时针排列)。当E在直线BC上运动时,点G是否在一条直线上运动?如果是,请你画出这条直线并证明;如果不是,也请说明理由;
(4)连接AG、CG,①求证:AG2-CE2是定值; ②求AG+CG的最小值(直接写出答案即可)。
18.如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
(1)AC的长等于 ;
(2)在线段AC上有一点D,满足AB2=AD AC,请在如图所示的网格中,用无刻度的直尺,画出点D,并简要说明点D的位置是如何找到的(不要求证明).
四、综合题
19.如图,居民楼与马路是平行的,在一楼的点A处测得它到马路的距离为9m,已知在距离载重汽车41m处就可受到噪声影响.
(1)试求在马路上以4m/s速度行驶的载重汽车,能给一楼A处的居民带来多长时间的噪音影响?
(2)若时间超过25秒,则此路禁止该车通行,你认为载重汽车可以在这条路上通行吗?
20.如图,一艘船由A港沿北偏东60°方向航行10km至B港,然后再沿北偏西30°方向航行10km至C港。
(1)求A,C两港之间的距离(结果保留到0.1km,参考数据: ≈1.414, ≈1.732);
(2)确定C港在A港的什么方向。
21.如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=6,CD=4,求:
(1)AB的长;
(2)四边形ABCD的面积.
22.在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(﹣4,6),(﹣1,4).
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC关于x轴对称的△A1B1C1;
(3)请在y轴上求作一点P,使△PB1C的周长最小,并写出点P的坐标.
23.如图1,纸上有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形.
(1)拼成的正方形的面积与边长分别是多少?
(2)如图2所示,以数轴的单位长度的线段为边作一个直角三角形,以数轴的﹣1点为圆心,直角三角形的最大边为半径画弧,交数轴正半轴于点A,那么点A表示的数是多少?点A表示的数的相反数是多少?
(3)如图3你能把十三个小正方形组成的图形纸,剪开并拼成正方形吗?若能,请画出示意图,并求它的边长是多少?
24.如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,点P从点A开始沿A B运动,速度为每秒1cm,点Q从点B开始沿B→C→A运动,速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求PQ的长;
(2)从出发几秒钟后,DPQB第一次能形成等腰三角形?
(3)当点Q在边CA上运动时,直接写出使△BCQ成为等腰三角形的运动时间.
参考答案
1.【答案】D
【解析】直角三角形的边满足勾股定理,已知直角三角形的两边长分别为3和4,则有两种情况,一种是这两边都是直角边;另一种是已知的两边一条是直角边,另一条是斜边.
【解答】当已知边3和4都是直角边,则第三边是斜边,长是;
当已知边3和4一条是直角边一条是斜边时,则第三边是直角边长是:=.
故选D.
2.【答案】A
【解析】勾股定理,如果一个三角形,两边的平方的和等于第三边的平方,则为直角三角形。
【解答】两棵树间的高度差为3米,间距为5米,
根据勾股定理:飞行距离最少是:
故选A.
3.【答案】D
【解析】解:过A作AD⊥BC于D,
∵AB=AC=5,AD⊥BC,
∴BD=BC=3,AD=,
当BP⊥AC时,BP最小=,
∴AP+BP+CP的最小值=AC+BP=5+4.8=9.8。
故答案为:D.
4.【答案】A
【解析】解:如图,连接AM,
∵AB=AC,点M为BC中点,
∴AM⊥CM,BM=CM=BC=3,
在Rt△ABM中,AB=5,BM=3,
∴AM=,
又∵S△AMC=MN AC=AM MC,
∴MN==.
故答案为:A.
5.【答案】D
【解析】解:由勾股定理得:
楼梯的水平宽度= =4,
∵地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
地毯的长度至少是3+4=7米.
故选D.
6.【答案】D
【解析】解:如图,作过点A的东西方向的直线AD,过点B作BC⊥AD于C,
则AC=6-1=5km,BC=9+3=12km,
在Rt△ABC中,由勾股定理求得AB= = =13(km).
所以登陆点A与宝藏埋藏点B之间的距离是13km.
故答案为:D.
7.【答案】D
【解析】解:A、∵大正方形的面积=c2=4×a(a+b)+(b-a)2,∴a2+b2=c2,正确;
B、大正方形的面积=(a+b)2=4×ab+c2,∴a2+b2=c2,正确;
C、梯形的面积=(a+b)(a+b)=2×ab+c2,∴a2+b2=c2,正确;
D、无法确定大正方形的边长,不能利用a、b、c来构造等式,错误;
故答案为:D.
8.【答案】B
【解析】解:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于P,连接CP.
此时DP+CP=DP+PC′=DC′的值最小.
∵DC=2,BD=6,
∴BC=8,
连接BC′,由对称性可知∠C′BA=∠CBA=45°,
∴∠CBC′=90°,
∴BC′⊥BC,∠BCC′=∠BC′C=45°,
∴BC=BC′=8,
根据勾股定理可得DC′= .故答案为:B.
9.【答案】C
【解析】设直角三角形的三边从小到大是a,b,c.在图1,可得 ,又因a2+b2=c2,所以 ;图2中, ,又因a2+b2=c2,所以 ,即可得 ,
故答案为:C.
10.【答案】D
【解析】根据四边形的总面积为4,可得出△ABF=△ACD=1,
△BCE的面积=
△ABC的面积=4-1-1-=,
在Rt△ADC中,AC=,
设AC 边上的高为x,
根据
可解得x=.
故答案为:D.
11.【答案】3
【解析】解:∵a、b是直角三角形的两条直角边,直角三角形的周长为6,斜边长为2.5,
∴a+b=3.5,a2+b2=2.52=6.25,
(a+b)2=12.25,
∴a2+b2+2ab=12.25,
∴2ab=6,
解得:ab=3.
故答案为:3.
12.【答案】
【解析】解:,
,
,
,
,,
∴△ABC≌△EFC(AAS),
,
在中
,
故答案为:.
13.【答案】14
【解析】解:连接AD,AE,
∵MN是AB的垂直平分线,
∴AE=BE,
∵△ABC是等腰三角形,D是BC的中点,
∴AD⊥BC,
∴△BDE的周长=BD+DE+BE=BD+DE+AE≥BD+AD,
当A、E、D三点共线时,△BDE的周长最小,
∵AB=AC=10,BC=12,即BD=6,
∴AD=8,
∴△BDE的周长最小值为BD+AD=6+8=14,
∴△BDE的周长最小值为14,
故答案为:14.
14.【答案】
【解析】解:如图,将△BCE绕点C逆时针旋转90°得到△ACF,连接DF,
∵∠ACB=90°,AC=BC=4 ,
∴AB=8,∠CAB=∠ABC,
∵AD=2,
∴BD=6=DE+BE,
∵将△BCE绕点C逆时针旋转90°得到△ACF
∴△AFC≌△BEC
∴AF=BE,CF=BC,∠FAC=∠ABC=45°=∠CAB,∠ACF=∠BCE,
∴∠FAD=90°
∵∠DCE=45°,∠ACB=90°,
∴∠ACD+∠BCE=45°,
∴∠ACD+∠FCA=45°=∠DCE,且CF=CE,CD=CD,
∴△FCD≌△ECD(SAS)
∴DE=DF,
在Rt△ADF中,DF2=AD2+AF2,
∴DE2=4+(6﹣DE)2,
∴DE= .
故答案为 .
15.【答案】38
【解析】解:设图2中的“数学风车”四个直角三角形的斜边长为x,AC=y,依题可得,
,
解得:,
∴这个风车的外围周长为:4×6.5+4×3=38.
故答案为:38.
16.【答案】解:在Rt△ABC中:
∵∠CAB=90°,BC=13米,AC=5米,
∴AB= =12(米),
∵此人以0.5米每秒的速度收绳,10秒后船移动到点D的位置,
∴CD=13﹣0.5×10=8(米),
∴AD= = = (米),
∴BD=AB﹣AD=12﹣ (米),
答:船向岸边移动了(12﹣ )米
17.【答案】(1)解:证明:∵△ABC和△ADE是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,∠B=60°,
∴∠BAD=∠CAE,∴△ABD △ACE,
∴∠ACE=∠B=60°.
(2)解:是;∵∠ACE=60°,∠ACB=60°,∴∠BCE=120°,
∴E在以CB为一条边的120°角的另一边上,
当点D与B重合,E与C重合;
当点D与C重合时,CE的长最长=AC;
故点E在一条线段上运动。
(3)解:是。证明:过G作GH⊥CD于H,∵四边形ABCD和四边形DEFG是正方形,
∴∠DCE=90°,∠EDG=90°,DE=DG,
∴∠EDC+∠GDC=90°,∠EDC+∠CED=90°,
∴∠GDC=∠CED,又∵DE=DG,∠DCE=∠GHD=90度,
∴△CDE △HGD,∴GH=CD=2.
又∵GH⊥CD,∴点G是在与CD的距离为2的直线上,过G作直线//CD,即点G在直线l上运动。
(4)解:①延长AD交直线l于P,由(1)可得△CDE △HGD,
∴CE=DH。
∵l//CD,GH⊥CD,∴∠DHG=∠PGH=90°,
又∵∠PDH=90°,∴四边形DHGP是矩形,
∴PG=DH=CE,PD=GH=2,
在Rt△AGP中,AG2-PG2=AP2=42=16,
∴AG2-CE2=AG2-PG2=16是定值。
②过A作关于l的对称点A′,连接A′C,交直线l于G′,则AG+CG≥A′G′+CG′=A′C,
在Rt△A′CD中,CD=2,A′D=6,∴A′C = 。
18.【答案】(1)5
(2)
【解析】(1)AC= ;
(2)如图,连接格点M和N,由图可知:
AB=AM=4,
BC=AN= ,
AC=MN= ,
∴△ABC≌△MAN,
∴∠AMN=∠BAC,
∴∠MAD+∠CAB=∠MAD+∠AMN=90°,
∴MN⊥AC,
易解得△MAN以MN为底时的高为 ,
∵AB2=AD AC,
∴AD=AB2÷AC= ,
综上可知,MN与AC的交点即为所求D点.
19.【答案】(1)解:∵由题意得AC=9,AB=AD=41,AC⊥BD,
∴Rt△ACB中,BC= ,
Rt△ACD中,DC= ,
∴BD=80,
∴80÷4=20(s),
∴受影响时间为20s
(2)解:∵20<25,
∴可以通行
20.【答案】(1) 由题意知,∠DAB+∠EBA=180°,
∠ABC=90°
∵AB=CB=10,
∴AC=
蓑衣AC约等于14.1km
(2)∠FCA-∠DAC=60°-45°=15°
21.【答案】(1)解:如图,延长AD,BC交于点E.
在Rt△ABE中,∠A=60°,∴∠E=30°.
在Rt△CDE中,CD=4,∠E=30°.∴CE=2CD=8.
∴BE=BC+CE=6+8=14.
设AB=x,则AE=2x,根据勾股定理得:x2+142=(2x)2,
解得x= ,则AB= 。
(2)解:在Rt△CDE中,∠CDE=90°,
∴DE= = =4 .
∴S四边形ABCD=S△ABE-S△CDE= ·AB·BE- ·CD·DE= × ×14- ×4×4 = .
22.【答案】(1)解:如图所示;
(2)解:如图,即为所求;
(3)解:作点B关于y轴的对称点B2,连接AB2交y轴于点P,则点P即为所求.
设直线AB2的解析式为y=kx+b(k≠0),
∵A(﹣4,6),B2(2,2),
∴ ,解得 ,
∴直线AB2的解析式为:y=﹣ x+ ,
∴当x=0时,y= ,
∴P(0, ).
23.【答案】(1)解:拼成的正方形的面积等于原来5个小正方形面积之和,即为5,
∵正方形的面积等于边长的平方,∴正方形的边长即为面积的算术平方根,为 ;
(2)解:设点A表示的数为x,则由题意可得:x-(-1)= ,∴x= ,
又∵ ,∴点A表示的数是 ,点A表示的数的相反数是 ;
(3)解:如图,
可以按如下方式把十三个小正方形组成的图形纸剪拼成正方形,其中三角形A可以平移至三角形C,三角形B可以平移至三角形D,由题意可知其边长为13的算术平方根,即 .
24.【答案】(1)解:当t=2时,则AP=2,BQ=2t=4,
∵AB=8cm,
∴BP=AB﹣AP=8﹣2=6(cm),
在Rt△BPQ中,由勾股定理可得PQ= (cm),
即PQ的长为2 cm
(2)解:由题意可知AP=t,BQ=2t,
∵AB=8,
∴BP=AB﹣AP=8﹣t,
当△PQB为等腰三角形时,则有BP=BQ,
即8﹣t=2t,
解得t= ,
∴出发 秒后△PQB能形成等腰三角形
(3)解:①当CQ=BQ时(如下图),则∠C=∠CBQ,
∵∠ABC=90°
∴∠CBQ+∠ABQ=90°
∠A+∠C=90°
∴∠A=∠ABQ
∴BQ=AQ
∴CQ=AQ=5
∴BC+CQ=11
∴t=11÷2=5.5秒
②当CQ=BC时(如图2),则BC+CQ=12
∴t=12÷2=6秒
③当BC=BQ时(如图3),过B点作BE⊥AC于点E,
则BE= ,
∴CE= ,
故CQ=2CE=7.2,
所以BC+CQ=13.2,
∴t=13.2÷2=6.6秒
综上:t的值为6.6秒或6秒或5.5秒时,△BCQ为等腰三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
