17.2 勾股定理的逆定理(知识讲解)同步学案(含解析)
文档属性
| 名称 | 17.2 勾股定理的逆定理(知识讲解)同步学案(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-16 16:47:52 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第十七章 勾股定理
17.2勾股定理的逆定理
【学习目标 】:
1. 掌握勾股定理的逆定理及其应用.理解原命题与其逆命题,原定理与其逆定理的概念及它们之间的关系.
2. 能利用勾股定理的逆定理,由三边之长判断一个三角形是否是直角三角形.
3. 能够理解勾股定理及逆定理的区别与联系,掌握它们的应用范围.
【知识讲解 】:
17.2.1、勾股定理的逆定理
如果三角形的三条边长,满足,那么这个三角形是直角三角形.
【特别说明】勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形,
最长边所对应的角为直角.
要点诠释:
(1)勾股定理的逆定理的作用是判定某一个三角形是否是直角三角形.
(2)勾股定理的逆定理是把“数”转为“形”,是通过计算来判定一个三角形是否为直角三角形.
17.2.2、如何判定一个三角形的形状(是否是直角三角形)
根据勾股定理的逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方,如果符合,则是直角三角形;反之则不是。
已知三角形三边的比例关系判断三角形形状:先设出参数,表示出三条边的长,再用勾股定理的逆定理判断其是否是直角三角形,如果此直角三角形的三边中有两个相同的数,那么该三角形还是等腰三角形;则为等腰直角三角形。
【典例1】判断下面以为边长的三角形是不是直角三角形?如果是,那么哪一个角是直角?
(1) (2)
解:(1),,
即
这个三角形是直角三角形,
且∠C是直角.
【典例2】若△ABC的三边满足 ,试判断△ABC的形状。
解:设
∵,
∴
即
∴△ABC是直角三角形,且∠C是直角.
【练习1】已知△ABC的三边,且,, ,试说明△ABC是直角三角形。
【练习2】若△ABC的三边满足, 试判断△ABC的形状。
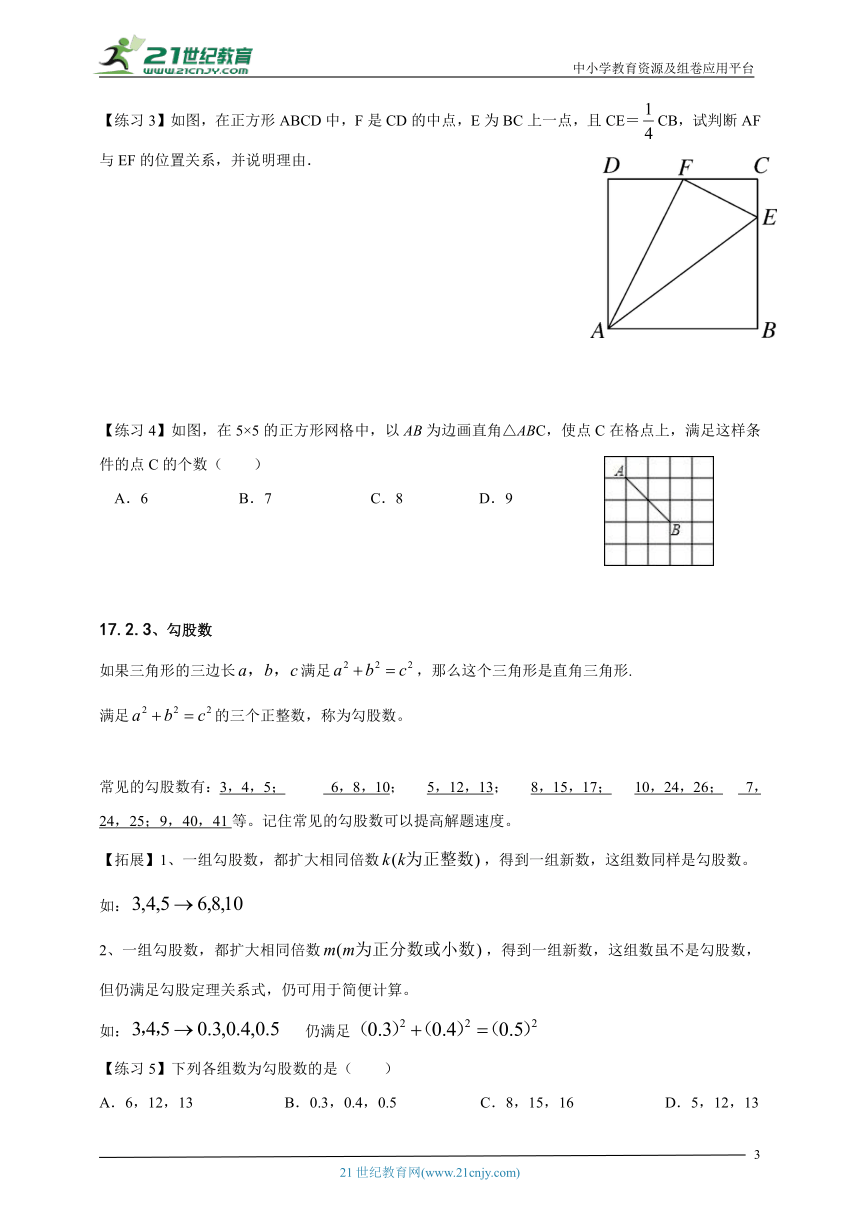
【练习3】如图,在正方形ABCD中,F是CD的中点,E为BC上一点,且CE=CB,试判断AF与EF的位置关系,并说明理由.
【练习4】如图,在5×5的正方形网格中,以AB为边画直角△ABC,使点C在格点上,满足这样条件的点C的个数( )
A.6 B.7 C.8 D.9
17.2.3、勾股数
如果三角形的三边长满足,那么这个三角形是直角三角形.
满足的三个正整数,称为勾股数。
常见的勾股数有:3,4,5; 6,8,10; 5,12,13; 8,15,17; 10,24,26; 7,24,25;9,40,41等。记住常见的勾股数可以提高解题速度。
【拓展】1、一组勾股数,都扩大相同倍数,得到一组新数,这组数同样是勾股数。
如:
2、一组勾股数,都扩大相同倍数,得到一组新数,这组数虽不是勾股数,但仍满足勾股定理关系式,仍可用于简便计算。
如: 仍满足
【练习5】下列各组数为勾股数的是( )
A.6,12,13 B.0.3,0.4,0.5 C.8,15,16 D.5,12,13
【练习6】下列各组数中,是勾股数的是( )
A. ,, B.40,41,9 C. ,1, D.0. 8,1.5,1.7
【练习7】周老师在一次“探究性学习”课中,设计了如下数表:
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:
a=_______;b=______;c=______;
(2)猜想:以a,b,c为边长的三角形是否是直角三角形?证明你的猜想.
(3)显然,满足这样关系的整数a,b,c我们把它叫做 数,请再写一组这样的数 (不同于表格中已出现的数组)
17.2.4、互逆命题和互逆定理
1. 命题:判断一件事情的语句叫命题。
命题1: 如果直角三角形的两条直角边长分别为,,斜边为,那么。
命题2 :如果三角形的三边长满足,那么这个三角形是直角三角形。
题设 结论
命题1 直角三角形
命题2 直角三角形
“命题1”和“命题2”是题设和结论正好相反的两个命题。
2.互逆命题:题设和结论正好相反的两个命题,叫做互逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题。
一般地,原命题成立时,它的逆命题既可能成立,也可能不成立。
3.互逆定理:如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理互为逆定理。
判断一个定理的逆命题与原定理是否为互逆定理,关键是确定它的逆命题的真假.
【练习8】说出下列命题的逆命题,并判断这些逆命题成立吗?
(1)两条直线平行,内错角相等;
(2)如果两个实数相等,那么它们的绝对值相等;
(3)全等三角形的对应角相等;
(4)在角的内部,到角的两边距离相等的点在角的平分线上。
17.2.5、勾股定理的逆定理的应用
【练习9】若一个三角形的三边长分别为6、8、10,则这个三角形最长边上的中线长为( )
A.3.6 B.4 C.4.8 D.5
【练习10】已知是△ABC三边的长,且满足关系式,则△ABC的形状是 .
【练习11】在△ABC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,问△ABC是什么形状的三角形?并说明你的理由.
【练习12】如图,在△ABC中,AB=5,AC=3,D是BC的中点,AD=2,求△ABC的面积.
【练习13】如图,在四边形ABCD中,AB=BC=2,CD=3,DA=1,且AB⊥BC于B.
求(1)∠BAD的度数; (2)四边形ABCD的面积.
【练习14】如图,每个小正方形的边长为1,A、B、C、D均在小正方形的顶点上.
(1)求线段AD的长度;
(2)∠BCD是直角吗?请说明你的理由.
【练习15】直角三角形有一条直角边的长是11,另外两边的长都是自然数,那么它的周长是( )
A.132 B.121 C.120 D.以上答案都不对
【练习16】已知:如图,四边形ABCD中,AB⊥BC,AB=2,BC=4,CD=4,AD=6,求四边形ABCD的面积.
【练习17】如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD 的面积.
【练习18】如图,南北方向PQ以东为我国领海,以西为公海,晚上10时28分,我国边防巡逻某艇在A处发现其正西方向的C处有一艘可疑船只正向我沿海靠近,便立即通知在PQ上B处巡逻的2号艇注意其动向,经检测,AC=10海里,BC=8海里,AB=6海里,若该船只的速度为12.8海里/时,则可疑船只最早何时进入我领海?
【练习19】一个零件的形状如图①所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图②所示,这个零件符合要求吗?
参考答案
【练习1】
【答案】解:
又
∴△ABC是直角三角形.
【练习2】
【答案】解:∵,
∴
即
∴
即.
∴△ABC是直角三角形.
【练习3】
【答案】 解:AF⊥EF.理由如下:
设正方形的边长为4a,
则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,
∴△AEF为直角三角形,且AE为斜边.
∴∠AFE=90°,即AF⊥EF.
【练习4】
【答案】C
【解析】解:根据题意可得以AB为边画直角△ABC,
使点C在格点上,满足这样条件的点C共 8个.故选C.
【练习5】
【答案】D
【解析】A选项:62+122≠132,故此选项错误;
B选项:32+42≠72,故此选项错误;
C选项:因为82+152≠162,故此选项错误;
D选项:52+122=132,故此选项正确.
故选D.
【练习6】【答案】B
【解析】A选项:,故此选项错误;
B选项:,故此选项正确;
C选项:因为勾股数是整数,故此选项错误;
D选项:因为勾股数是整数,故此选项错误.
故选B.
【练习7】
【答案】(1),, (2)是直角三角形
(3)(答案不唯一)
【解析】
(1)观察、分析可得:,,;
(2)猜想:以a,b,c为边长的三角形是直角三角形,
理由如下:∵,,,
∴,,
∴
∴以为边的三角形是直角三角形;
(3)由“勾股数”的定义可知,满足这样关系的整数我们把它叫做勾股数,这样的勾股数有很多,如(答案不唯一).
【练习8】
【答案】(1)内错角相等,两条直线平行;成立
(2)如果两个实数的绝对值相等,那么它们相等. ;不成立
(3)对应角相等的三角形全等 . ;不成立
(4)在角平分线上的点到角两边的距离相等. ;成立
【练习9】
【答案】D
【解析】解:∵
∴三边长分别为6cm、8cm、10cm的三角形是直角三角形,最大边是斜边为10cm.
∴最大边上的中线长为5cm.
【练习10】
【答案】等腰直角三角形
【解析】解:∵,
∴,,
解得:,,
∴△ABC的形状是等腰直角三角形,故答案为:等腰直角三角形.
【练习11】
【答案】△ABC是等腰三角形
【解析】解:△ABC是等腰三角形,理由如下:
∵AD是BC边的中线,BC=16cm,
∴BD=DC=8cm,
∵AD2+BD2=152+82=172=AB2,
∴∠ADB=90°,
∴∠ADC=90°,
在Rt△ADC中,AC==17cm.
∴AC=AB,即△ABC是等腰三角形.
【练习12】
【答案】6
【解析】解:延长AD至E,使ED=AD=2,连接BE,如图所示:则AE=4,
∵D是BC的中点,
∴BD=CD,
在△BED和△ACD中,
∴△BED≌△ACD(SAS),
∴BE=AC=3,
∵AE=4,AB=5,BE=3,
∴AE2+BE2=AB2,
∴△ABE是直角三角形,
∴△ABC的面积=△ABE的面积=×3×4=6.
【练习13】
【答案】(1)∠BAD=135° (2)
【解析】解:
(1)连接AC,
∵∠B=90°,AB=BC=2,
∴AC==,∠BAC=45°,
又∵CD=3,DA=1,
∴AC2+DA2=8+1=9,CD2=9,
∴AC2+DA2=CD2,
∴△ACD是直角三角形,
∴∠CAD=90°,
∴∠BAD=45°+90°=135°.
(2)∴
【练习14】【答案】(1)AD=5 (2)∠BCD是直角
解:(1)AD==5;
(2)∠BCD是直角.理由:连接BD,
∵DC2=12+22=5,BC2=22+42=20,BD2=32+42=25,
∴CD2+BC2=BD2,
∴△BCD是直角三角形,
∴∠BCD是直角.
【练习15】
【答案】A
【解析】解:设另外两边是a、b(a>b)
则根据勾股定理,得:a 2﹣b2=121
∵另外两边的长都是自然数
∴(a +b)(a﹣b)=121=121×1
即另外两边的和是121,
故三角形的周长是121+11=132.故选A.
【练习16】
【答案】
解:连接AC.
∵∠ABC=90°,AB=2,BC=4,
∴AC==,
在△ACD中,AC2+CD2=20+16=36=AD2,
∴△ACD是直角三角形,
∴=AB BC+AC CD=×2×4+××4=.
故四边形ABCD的面积为
【练习17】
【答案】解:连接BD.
在Rt△ABD中,AD=3cm,AB=4cm
由勾股定理得 BD2=AB2+AD2,
∴BD=5m.
又∵ CD=12cm,BC=13cm,
∴ BC2=CD2+BD2,
∴△BDC是直角三角形.
∴(cm2)
【练习18】
【答案】解:∵AC=10,AB=6,BC=8,
∴AC2=AB2+BC2,
即△ABC是直角三角形.
设PQ与AC相交于点D,
根据三角形面积公式有 BC·AB=AC·BD,
即6×8=10BD,解得BD=4.8
在Rt△BCD中,(海里)
又∵该船只的速度为12.8海里/时,
6.4÷12.8=0.5(小时)=30(分钟),
∴需要30分钟进入我领海,即最早晚上10时58分进入我领海.
【练习19】
【答案】解:在△ABD中,
∴△ABD 是直角三角形,∠A是直角.
在△BCD中,
∴△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十七章 勾股定理
17.2勾股定理的逆定理
【学习目标 】:
1. 掌握勾股定理的逆定理及其应用.理解原命题与其逆命题,原定理与其逆定理的概念及它们之间的关系.
2. 能利用勾股定理的逆定理,由三边之长判断一个三角形是否是直角三角形.
3. 能够理解勾股定理及逆定理的区别与联系,掌握它们的应用范围.
【知识讲解 】:
17.2.1、勾股定理的逆定理
如果三角形的三条边长,满足,那么这个三角形是直角三角形.
【特别说明】勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形,
最长边所对应的角为直角.
要点诠释:
(1)勾股定理的逆定理的作用是判定某一个三角形是否是直角三角形.
(2)勾股定理的逆定理是把“数”转为“形”,是通过计算来判定一个三角形是否为直角三角形.
17.2.2、如何判定一个三角形的形状(是否是直角三角形)
根据勾股定理的逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方,如果符合,则是直角三角形;反之则不是。
已知三角形三边的比例关系判断三角形形状:先设出参数,表示出三条边的长,再用勾股定理的逆定理判断其是否是直角三角形,如果此直角三角形的三边中有两个相同的数,那么该三角形还是等腰三角形;则为等腰直角三角形。
【典例1】判断下面以为边长的三角形是不是直角三角形?如果是,那么哪一个角是直角?
(1) (2)
解:(1),,
即
这个三角形是直角三角形,
且∠C是直角.
【典例2】若△ABC的三边满足 ,试判断△ABC的形状。
解:设
∵,
∴
即
∴△ABC是直角三角形,且∠C是直角.
【练习1】已知△ABC的三边,且,, ,试说明△ABC是直角三角形。
【练习2】若△ABC的三边满足, 试判断△ABC的形状。
【练习3】如图,在正方形ABCD中,F是CD的中点,E为BC上一点,且CE=CB,试判断AF与EF的位置关系,并说明理由.
【练习4】如图,在5×5的正方形网格中,以AB为边画直角△ABC,使点C在格点上,满足这样条件的点C的个数( )
A.6 B.7 C.8 D.9
17.2.3、勾股数
如果三角形的三边长满足,那么这个三角形是直角三角形.
满足的三个正整数,称为勾股数。
常见的勾股数有:3,4,5; 6,8,10; 5,12,13; 8,15,17; 10,24,26; 7,24,25;9,40,41等。记住常见的勾股数可以提高解题速度。
【拓展】1、一组勾股数,都扩大相同倍数,得到一组新数,这组数同样是勾股数。
如:
2、一组勾股数,都扩大相同倍数,得到一组新数,这组数虽不是勾股数,但仍满足勾股定理关系式,仍可用于简便计算。
如: 仍满足
【练习5】下列各组数为勾股数的是( )
A.6,12,13 B.0.3,0.4,0.5 C.8,15,16 D.5,12,13
【练习6】下列各组数中,是勾股数的是( )
A. ,, B.40,41,9 C. ,1, D.0. 8,1.5,1.7
【练习7】周老师在一次“探究性学习”课中,设计了如下数表:
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:
a=_______;b=______;c=______;
(2)猜想:以a,b,c为边长的三角形是否是直角三角形?证明你的猜想.
(3)显然,满足这样关系的整数a,b,c我们把它叫做 数,请再写一组这样的数 (不同于表格中已出现的数组)
17.2.4、互逆命题和互逆定理
1. 命题:判断一件事情的语句叫命题。
命题1: 如果直角三角形的两条直角边长分别为,,斜边为,那么。
命题2 :如果三角形的三边长满足,那么这个三角形是直角三角形。
题设 结论
命题1 直角三角形
命题2 直角三角形
“命题1”和“命题2”是题设和结论正好相反的两个命题。
2.互逆命题:题设和结论正好相反的两个命题,叫做互逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题。
一般地,原命题成立时,它的逆命题既可能成立,也可能不成立。
3.互逆定理:如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理互为逆定理。
判断一个定理的逆命题与原定理是否为互逆定理,关键是确定它的逆命题的真假.
【练习8】说出下列命题的逆命题,并判断这些逆命题成立吗?
(1)两条直线平行,内错角相等;
(2)如果两个实数相等,那么它们的绝对值相等;
(3)全等三角形的对应角相等;
(4)在角的内部,到角的两边距离相等的点在角的平分线上。
17.2.5、勾股定理的逆定理的应用
【练习9】若一个三角形的三边长分别为6、8、10,则这个三角形最长边上的中线长为( )
A.3.6 B.4 C.4.8 D.5
【练习10】已知是△ABC三边的长,且满足关系式,则△ABC的形状是 .
【练习11】在△ABC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,问△ABC是什么形状的三角形?并说明你的理由.
【练习12】如图,在△ABC中,AB=5,AC=3,D是BC的中点,AD=2,求△ABC的面积.
【练习13】如图,在四边形ABCD中,AB=BC=2,CD=3,DA=1,且AB⊥BC于B.
求(1)∠BAD的度数; (2)四边形ABCD的面积.
【练习14】如图,每个小正方形的边长为1,A、B、C、D均在小正方形的顶点上.
(1)求线段AD的长度;
(2)∠BCD是直角吗?请说明你的理由.
【练习15】直角三角形有一条直角边的长是11,另外两边的长都是自然数,那么它的周长是( )
A.132 B.121 C.120 D.以上答案都不对
【练习16】已知:如图,四边形ABCD中,AB⊥BC,AB=2,BC=4,CD=4,AD=6,求四边形ABCD的面积.
【练习17】如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD 的面积.
【练习18】如图,南北方向PQ以东为我国领海,以西为公海,晚上10时28分,我国边防巡逻某艇在A处发现其正西方向的C处有一艘可疑船只正向我沿海靠近,便立即通知在PQ上B处巡逻的2号艇注意其动向,经检测,AC=10海里,BC=8海里,AB=6海里,若该船只的速度为12.8海里/时,则可疑船只最早何时进入我领海?
【练习19】一个零件的形状如图①所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图②所示,这个零件符合要求吗?
参考答案
【练习1】
【答案】解:
又
∴△ABC是直角三角形.
【练习2】
【答案】解:∵,
∴
即
∴
即.
∴△ABC是直角三角形.
【练习3】
【答案】 解:AF⊥EF.理由如下:
设正方形的边长为4a,
则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,
∴△AEF为直角三角形,且AE为斜边.
∴∠AFE=90°,即AF⊥EF.
【练习4】
【答案】C
【解析】解:根据题意可得以AB为边画直角△ABC,
使点C在格点上,满足这样条件的点C共 8个.故选C.
【练习5】
【答案】D
【解析】A选项:62+122≠132,故此选项错误;
B选项:32+42≠72,故此选项错误;
C选项:因为82+152≠162,故此选项错误;
D选项:52+122=132,故此选项正确.
故选D.
【练习6】【答案】B
【解析】A选项:,故此选项错误;
B选项:,故此选项正确;
C选项:因为勾股数是整数,故此选项错误;
D选项:因为勾股数是整数,故此选项错误.
故选B.
【练习7】
【答案】(1),, (2)是直角三角形
(3)(答案不唯一)
【解析】
(1)观察、分析可得:,,;
(2)猜想:以a,b,c为边长的三角形是直角三角形,
理由如下:∵,,,
∴,,
∴
∴以为边的三角形是直角三角形;
(3)由“勾股数”的定义可知,满足这样关系的整数我们把它叫做勾股数,这样的勾股数有很多,如(答案不唯一).
【练习8】
【答案】(1)内错角相等,两条直线平行;成立
(2)如果两个实数的绝对值相等,那么它们相等. ;不成立
(3)对应角相等的三角形全等 . ;不成立
(4)在角平分线上的点到角两边的距离相等. ;成立
【练习9】
【答案】D
【解析】解:∵
∴三边长分别为6cm、8cm、10cm的三角形是直角三角形,最大边是斜边为10cm.
∴最大边上的中线长为5cm.
【练习10】
【答案】等腰直角三角形
【解析】解:∵,
∴,,
解得:,,
∴△ABC的形状是等腰直角三角形,故答案为:等腰直角三角形.
【练习11】
【答案】△ABC是等腰三角形
【解析】解:△ABC是等腰三角形,理由如下:
∵AD是BC边的中线,BC=16cm,
∴BD=DC=8cm,
∵AD2+BD2=152+82=172=AB2,
∴∠ADB=90°,
∴∠ADC=90°,
在Rt△ADC中,AC==17cm.
∴AC=AB,即△ABC是等腰三角形.
【练习12】
【答案】6
【解析】解:延长AD至E,使ED=AD=2,连接BE,如图所示:则AE=4,
∵D是BC的中点,
∴BD=CD,
在△BED和△ACD中,
∴△BED≌△ACD(SAS),
∴BE=AC=3,
∵AE=4,AB=5,BE=3,
∴AE2+BE2=AB2,
∴△ABE是直角三角形,
∴△ABC的面积=△ABE的面积=×3×4=6.
【练习13】
【答案】(1)∠BAD=135° (2)
【解析】解:
(1)连接AC,
∵∠B=90°,AB=BC=2,
∴AC==,∠BAC=45°,
又∵CD=3,DA=1,
∴AC2+DA2=8+1=9,CD2=9,
∴AC2+DA2=CD2,
∴△ACD是直角三角形,
∴∠CAD=90°,
∴∠BAD=45°+90°=135°.
(2)∴
【练习14】【答案】(1)AD=5 (2)∠BCD是直角
解:(1)AD==5;
(2)∠BCD是直角.理由:连接BD,
∵DC2=12+22=5,BC2=22+42=20,BD2=32+42=25,
∴CD2+BC2=BD2,
∴△BCD是直角三角形,
∴∠BCD是直角.
【练习15】
【答案】A
【解析】解:设另外两边是a、b(a>b)
则根据勾股定理,得:a 2﹣b2=121
∵另外两边的长都是自然数
∴(a +b)(a﹣b)=121=121×1
即另外两边的和是121,
故三角形的周长是121+11=132.故选A.
【练习16】
【答案】
解:连接AC.
∵∠ABC=90°,AB=2,BC=4,
∴AC==,
在△ACD中,AC2+CD2=20+16=36=AD2,
∴△ACD是直角三角形,
∴=AB BC+AC CD=×2×4+××4=.
故四边形ABCD的面积为
【练习17】
【答案】解:连接BD.
在Rt△ABD中,AD=3cm,AB=4cm
由勾股定理得 BD2=AB2+AD2,
∴BD=5m.
又∵ CD=12cm,BC=13cm,
∴ BC2=CD2+BD2,
∴△BDC是直角三角形.
∴(cm2)
【练习18】
【答案】解:∵AC=10,AB=6,BC=8,
∴AC2=AB2+BC2,
即△ABC是直角三角形.
设PQ与AC相交于点D,
根据三角形面积公式有 BC·AB=AC·BD,
即6×8=10BD,解得BD=4.8
在Rt△BCD中,(海里)
又∵该船只的速度为12.8海里/时,
6.4÷12.8=0.5(小时)=30(分钟),
∴需要30分钟进入我领海,即最早晚上10时58分进入我领海.
【练习19】
【答案】解:在△ABD中,
∴△ABD 是直角三角形,∠A是直角.
在△BCD中,
∴△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
