《探索活动:平行四边形的面积》(课件)-五年级上册数学北师大版(共34张PPT)
文档属性
| 名称 | 《探索活动:平行四边形的面积》(课件)-五年级上册数学北师大版(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 606.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 00:00:00 | ||
图片预览





文档简介
(共34张PPT)
2
0
2
2
第四单元:多边形的面积
探索活动-平行四边形的面积
目录
知识讲解
实战演练
01
知识讲解
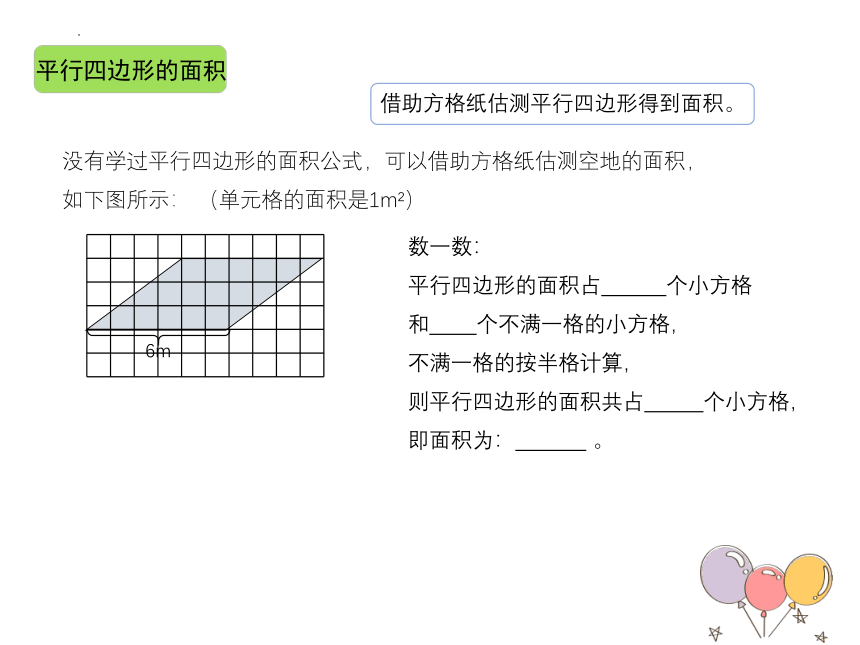
平行四边形的面积
借助方格纸估测平行四边形得到面积。
没有学过平行四边形的面积公式,可以借助方格纸估测空地的面积,
如下图所示: (单元格的面积是1m )
6m
数一数:
平行四边形的面积占 个小方格
和 个不满一格的小方格,
不满一格的按半格计算,
则平行四边形的面积共占 个小方格,
即面积为: 。
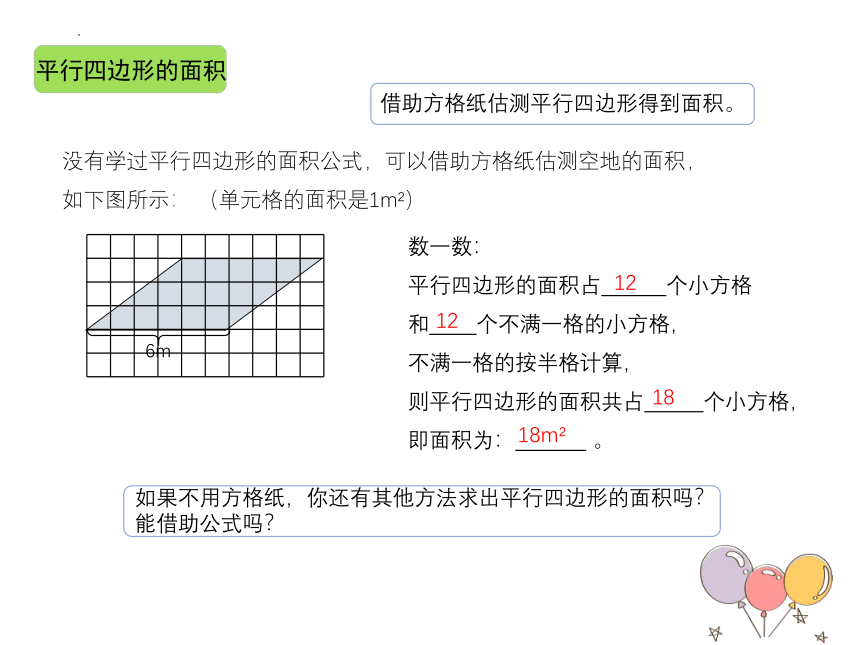
平行四边形的面积
借助方格纸估测平行四边形得到面积。
没有学过平行四边形的面积公式,可以借助方格纸估测空地的面积,
如下图所示: (单元格的面积是1m )
6m
数一数:
平行四边形的面积占 个小方格
和 个不满一格的小方格,
不满一格的按半格计算,
则平行四边形的面积共占 个小方格,
即面积为: 。
12
12
18
18m
如果不用方格纸,你还有其他方法求出平行四边形的面积吗?
能借助公式吗?
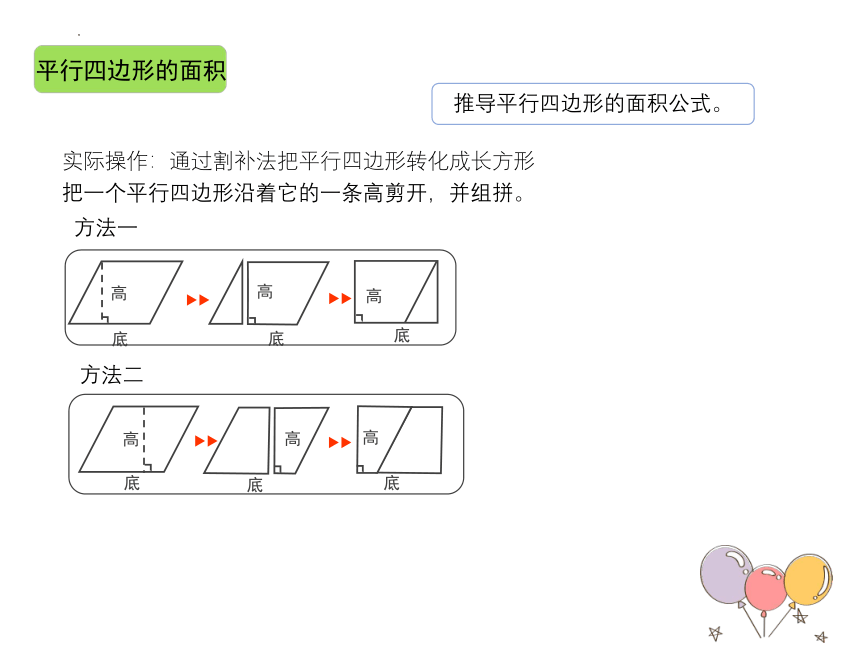
平行四边形的面积
推导平行四边形的面积公式。
实际操作:通过割补法把平行四边形转化成长方形
把一个平行四边形沿着它的一条高剪开,并组拼。
高
底
高
底
高
底
高
底
高
底
高
底
方法一
方法二
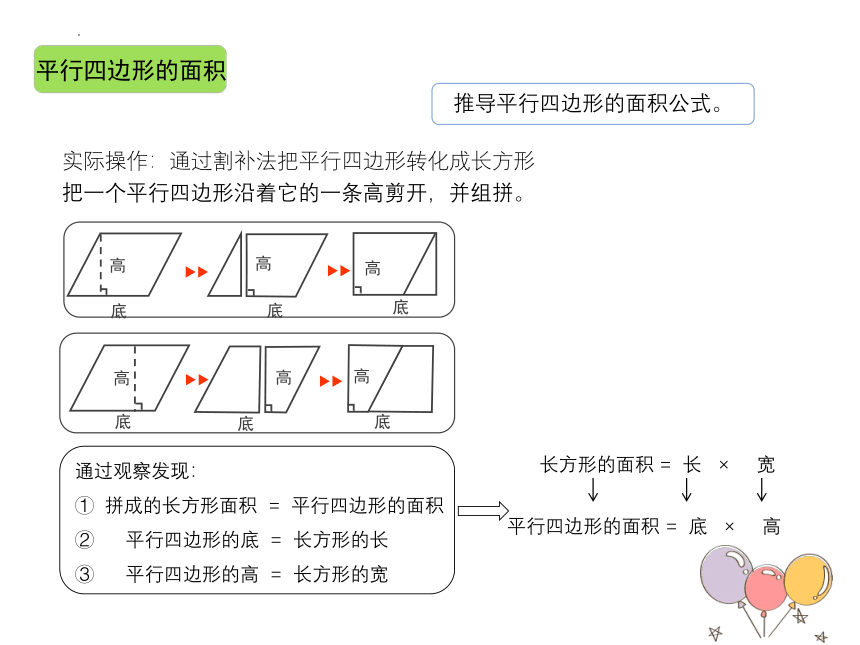
平行四边形的面积
推导平行四边形的面积公式。
实际操作:通过割补法把平行四边形转化成长方形
把一个平行四边形沿着它的一条高剪开,并组拼。
高
底
高
底
高
底
高
底
高
底
高
底
通过观察发现:
① 拼成的长方形面积 = 平行四边形的面积
② 平行四边形的底 = 长方形的长
③ 平行四边形的高 = 长方形的宽
长方形的面积 = 长 × 宽
平行四边形的面积 = 底 × 高
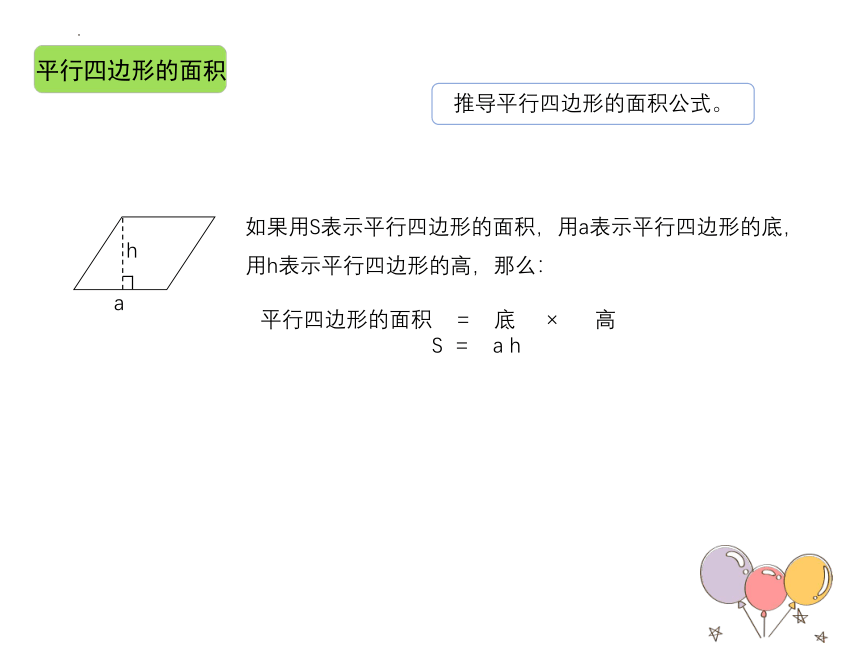
平行四边形的面积
推导平行四边形的面积公式。
如果用S表示平行四边形的面积,用a表示平行四边形的底,
用h表示平行四边形的高,那么:
h
a
平行四边形的面积 = 底 × 高
S = a h
平行四边形的面积
归纳总结。
平行四边形的面积=底×高
字母表示:S=ah
h
a
已知S、a、h其中两个量,可以求第3个量:
a=S÷h、h=S÷a
技 巧 点 拨
平行四边形的面积:S=ah
注意:平行四边形的面积要用一组对应的底和高相乘。
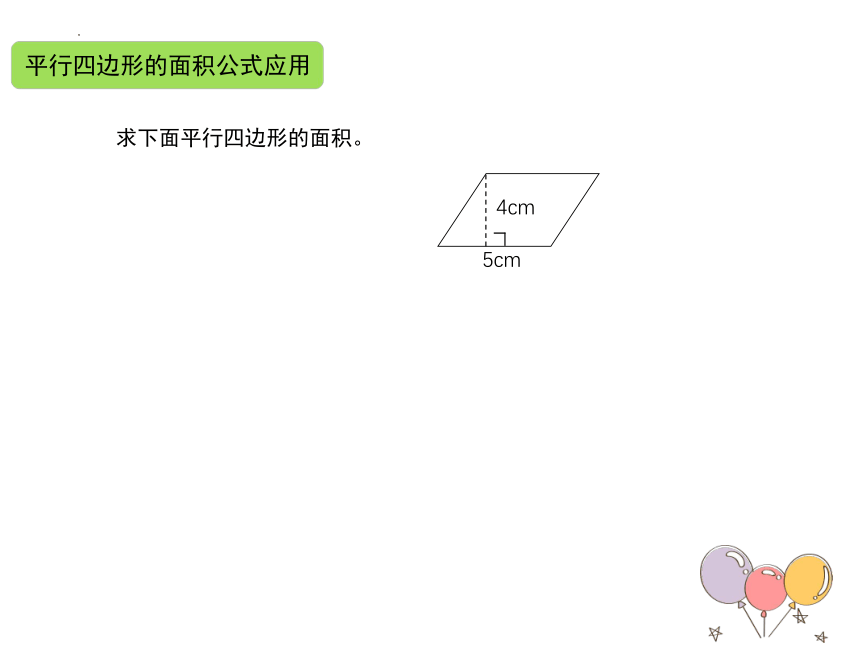
求下面平行四边形的面积。
4cm
5cm
平行四边形的面积公式应用
求下面平行四边形的面积。
4cm
5cm
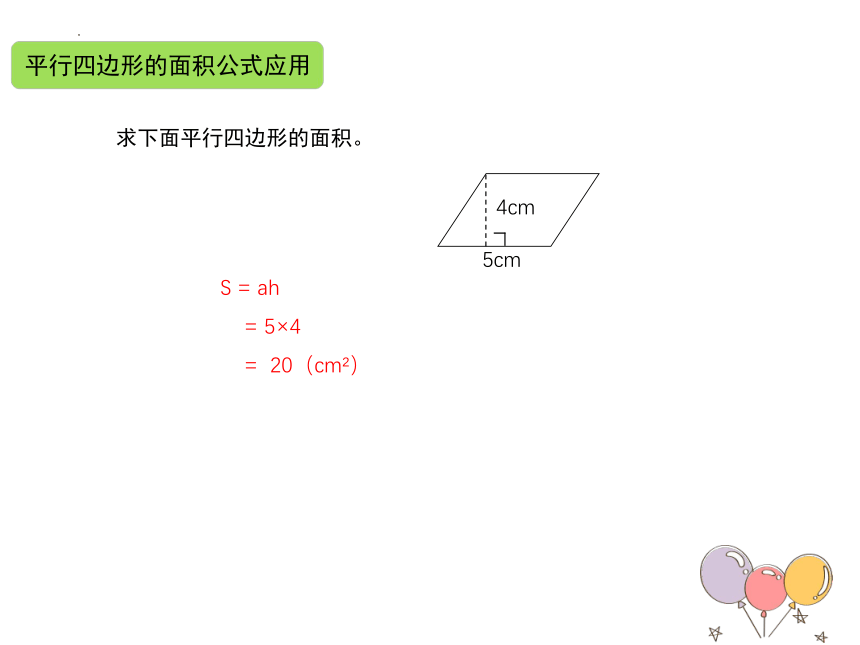
平行四边形的面积公式应用
S = ah
= 5×4
= 20(cm )
一个平行四边形广告牌的面积是12.8m ,高是0.8m,这条高对应的底边长是多少米?
思考:
平行四边形的面积公式应用
一个平行四边形广告牌的面积是12.8m ,高是0.8m,这条高对应的底边长是多少米?
思考:
平行四边形的面积公式应用
方法一:由S=ah可以推出,a=S÷h
12.8÷0.8=16(m)
答:这条高对应的底边长是16m。
一个平行四边形广告牌的面积是12.8m ,高是0.8m,这条高对应的底边长是多少米?
思考:
平行四边形的面积公式应用
方法二:根据平行四边形的面积公式列方程
解:设这条高对应的底边长是xm。
0.8x=12.8
x=12.8÷0.8
x= 16
答:这条高对应的底边长是16m。
平行四边形的面积公式应用
如下图所示,求出BC边上的高DE的长。
3.2cm
3cm
A
B
C
D
E
F
4cm
平行四边形的面积公式应用
如下图所示,求出BC边上的高DE的长。
3.2cm
3cm
A
B
C
D
E
F
4cm
根据平行四边形的面积=底×高,
可得S=AB×DF=BC×DE,由此可以得出:
DE=AB×DF÷BC
平行四边形的面积公式应用
如下图所示,求出BC边上的高DE的长。
3.2cm
3cm
A
B
C
D
E
F
4cm
DE=3×3.2÷4
= 9.6÷4
= 2.4(cm)
答:BC边上的高DE的长是2.4cm。
技 巧 点 拨
在同一个平行四边形中,不同的底与它对应的高的乘积相等,都等于平行四边形的面积。
平行四边形的面积公式应用
等底等高的平行四边形面积间的关系。
分别计算图中每个平行四边形的面积,你发现了什么?
思考:
5cm
③
①
②
2cm
平行四边形的面积公式应用
等底等高的平行四边形面积间的关系。
分别计算图中每个平行四边形的面积,你发现了什么?
思考:
5cm
③
①
②
2cm
图中三个平行四边形的底和高分别相等,
求出三个平行四边形的面积,并找出其中的规律。
平行四边形的面积公式应用
等底等高的平行四边形面积间的关系。
分别计算图中每个平行四边形的面积,你发现了什么?
思考:
5cm
③
①
②
2cm
①的面积:2×5=10(cm )
②的面积:2×5=10(cm )
③的面积:2×5=10(cm )
图①的面积=图②的面积=图③的面积
规律: 。
平行四边形的面积公式应用
等底等高的平行四边形面积间的关系。
分别计算图中每个平行四边形的面积,你发现了什么?
思考:
5cm
③
①
②
2cm
①的面积:2×5=10(cm )
②的面积:2×5=10(cm )
③的面积:2×5=10(cm )
图①的面积=图②的面积=图③的面积
规律: 。
等底等高的平行四边形的面积相等。
技 巧 点 拨
平行四边形的底和高都相等,它们的面积也相等,
简记为:
等底等高的平行四边形的面积相等。
02
实战演练
实战演练
判断题。
(1)周长相等的平行四边形与长方形,它们的面积也相等。
( )
(2)平行四边形的底越长,它的面积就越大。
( )
(3)等底等高的两个平行四边形,面积一定相等。
( )
(4)两个面积相等的平行四边形,底和高一定也分别相等。
( )
实战演练
判断题。
(1)周长相等的平行四边形与长方形,它们的面积也相等。
( )
(2)平行四边形的底越长,它的面积就越大。
( )
(3)等底等高的两个平行四边形,面积一定相等。
( )
(4)两个面积相等的平行四边形,底和高一定也分别相等。
( )
×
×
√
×
实战演练
填空。
(1)把一个平行四边形沿其中一条高剪开,平移后可以拼成一个( ),长方形的长就是平行四边形的( ),长方形的宽就是平行四边形的( )。
(2)一个平行四边形的周长为46cm,一边的长为14cm,另外三边的长分是( )、( )、( )。
(3)平行四边形的高是5cm,底是高的2倍,它的面积是( )cm 。
(4)填表(单位:cm)。
底 高 平行四边形的面积
0.7 50
8 9.6
0.02 6
实战演练
填空。
(1)把一个平行四边形沿其中一条高剪开,平移后可以拼成一个( ),长方形的长就是平行四边形的( ),长方形的宽就是平行四边形的( )。
(2)一个平行四边形的周长为46cm,一边的长为14cm,另外三边的长分是( )、( )、( )。
(3)平行四边形的高是5cm,底是高的2倍,它的面积是( )cm 。
(4)填表(单位:cm)。
底 高 平行四边形的面积
0.7 50 35
8 1.2 9.6
300 0.02 6
长方形
底
高
14cm
9cm
9cm
50
实战演练
有一块平行四边形草地,底长24m,高是底的一半。如果每平方米的草可供3只羊吃一天,这块草地可供多少只羊吃一天?
实战演练
有一块平行四边形草地,底长24m,高是底的一半。如果每平方米的草可供3只羊吃一天,这块草地可供多少只羊吃一天?
面积:S=24×(24÷2)=288(m )
288×3=864(只)
答:这块草地可供864只羊吃一天。
实战演练
用木条制成一个长方形的框架,长是18cm,宽是15cm,它的周长和面积各是多少?如果把它拉成平行四边形,那么周长和面积会发生怎么样的变化?
实战演练
用木条制成一个长方形的框架,长是18cm,宽是15cm,它的周长和面积各是多少?如果把它拉成平行四边形,那么周长和面积会发生怎么样的变化?
长方形的周长: (18+15)×2=66(cm)
长方形的面积:18×15=270(cm )
因为无论怎样变化周长总是四条边的和,所以周长不变。
平行四边形的面积是底乘以高,在变化过程中底是不变的,高是变化的,且高<长方形的宽,所以如果拉成平行四边形,面积会变小 。
2
0
2
2
Thanks for listening.
Welcome to ask questions
2
0
2
2
第四单元:多边形的面积
探索活动-平行四边形的面积
目录
知识讲解
实战演练
01
知识讲解
平行四边形的面积
借助方格纸估测平行四边形得到面积。
没有学过平行四边形的面积公式,可以借助方格纸估测空地的面积,
如下图所示: (单元格的面积是1m )
6m
数一数:
平行四边形的面积占 个小方格
和 个不满一格的小方格,
不满一格的按半格计算,
则平行四边形的面积共占 个小方格,
即面积为: 。
平行四边形的面积
借助方格纸估测平行四边形得到面积。
没有学过平行四边形的面积公式,可以借助方格纸估测空地的面积,
如下图所示: (单元格的面积是1m )
6m
数一数:
平行四边形的面积占 个小方格
和 个不满一格的小方格,
不满一格的按半格计算,
则平行四边形的面积共占 个小方格,
即面积为: 。
12
12
18
18m
如果不用方格纸,你还有其他方法求出平行四边形的面积吗?
能借助公式吗?
平行四边形的面积
推导平行四边形的面积公式。
实际操作:通过割补法把平行四边形转化成长方形
把一个平行四边形沿着它的一条高剪开,并组拼。
高
底
高
底
高
底
高
底
高
底
高
底
方法一
方法二
平行四边形的面积
推导平行四边形的面积公式。
实际操作:通过割补法把平行四边形转化成长方形
把一个平行四边形沿着它的一条高剪开,并组拼。
高
底
高
底
高
底
高
底
高
底
高
底
通过观察发现:
① 拼成的长方形面积 = 平行四边形的面积
② 平行四边形的底 = 长方形的长
③ 平行四边形的高 = 长方形的宽
长方形的面积 = 长 × 宽
平行四边形的面积 = 底 × 高
平行四边形的面积
推导平行四边形的面积公式。
如果用S表示平行四边形的面积,用a表示平行四边形的底,
用h表示平行四边形的高,那么:
h
a
平行四边形的面积 = 底 × 高
S = a h
平行四边形的面积
归纳总结。
平行四边形的面积=底×高
字母表示:S=ah
h
a
已知S、a、h其中两个量,可以求第3个量:
a=S÷h、h=S÷a
技 巧 点 拨
平行四边形的面积:S=ah
注意:平行四边形的面积要用一组对应的底和高相乘。
求下面平行四边形的面积。
4cm
5cm
平行四边形的面积公式应用
求下面平行四边形的面积。
4cm
5cm
平行四边形的面积公式应用
S = ah
= 5×4
= 20(cm )
一个平行四边形广告牌的面积是12.8m ,高是0.8m,这条高对应的底边长是多少米?
思考:
平行四边形的面积公式应用
一个平行四边形广告牌的面积是12.8m ,高是0.8m,这条高对应的底边长是多少米?
思考:
平行四边形的面积公式应用
方法一:由S=ah可以推出,a=S÷h
12.8÷0.8=16(m)
答:这条高对应的底边长是16m。
一个平行四边形广告牌的面积是12.8m ,高是0.8m,这条高对应的底边长是多少米?
思考:
平行四边形的面积公式应用
方法二:根据平行四边形的面积公式列方程
解:设这条高对应的底边长是xm。
0.8x=12.8
x=12.8÷0.8
x= 16
答:这条高对应的底边长是16m。
平行四边形的面积公式应用
如下图所示,求出BC边上的高DE的长。
3.2cm
3cm
A
B
C
D
E
F
4cm
平行四边形的面积公式应用
如下图所示,求出BC边上的高DE的长。
3.2cm
3cm
A
B
C
D
E
F
4cm
根据平行四边形的面积=底×高,
可得S=AB×DF=BC×DE,由此可以得出:
DE=AB×DF÷BC
平行四边形的面积公式应用
如下图所示,求出BC边上的高DE的长。
3.2cm
3cm
A
B
C
D
E
F
4cm
DE=3×3.2÷4
= 9.6÷4
= 2.4(cm)
答:BC边上的高DE的长是2.4cm。
技 巧 点 拨
在同一个平行四边形中,不同的底与它对应的高的乘积相等,都等于平行四边形的面积。
平行四边形的面积公式应用
等底等高的平行四边形面积间的关系。
分别计算图中每个平行四边形的面积,你发现了什么?
思考:
5cm
③
①
②
2cm
平行四边形的面积公式应用
等底等高的平行四边形面积间的关系。
分别计算图中每个平行四边形的面积,你发现了什么?
思考:
5cm
③
①
②
2cm
图中三个平行四边形的底和高分别相等,
求出三个平行四边形的面积,并找出其中的规律。
平行四边形的面积公式应用
等底等高的平行四边形面积间的关系。
分别计算图中每个平行四边形的面积,你发现了什么?
思考:
5cm
③
①
②
2cm
①的面积:2×5=10(cm )
②的面积:2×5=10(cm )
③的面积:2×5=10(cm )
图①的面积=图②的面积=图③的面积
规律: 。
平行四边形的面积公式应用
等底等高的平行四边形面积间的关系。
分别计算图中每个平行四边形的面积,你发现了什么?
思考:
5cm
③
①
②
2cm
①的面积:2×5=10(cm )
②的面积:2×5=10(cm )
③的面积:2×5=10(cm )
图①的面积=图②的面积=图③的面积
规律: 。
等底等高的平行四边形的面积相等。
技 巧 点 拨
平行四边形的底和高都相等,它们的面积也相等,
简记为:
等底等高的平行四边形的面积相等。
02
实战演练
实战演练
判断题。
(1)周长相等的平行四边形与长方形,它们的面积也相等。
( )
(2)平行四边形的底越长,它的面积就越大。
( )
(3)等底等高的两个平行四边形,面积一定相等。
( )
(4)两个面积相等的平行四边形,底和高一定也分别相等。
( )
实战演练
判断题。
(1)周长相等的平行四边形与长方形,它们的面积也相等。
( )
(2)平行四边形的底越长,它的面积就越大。
( )
(3)等底等高的两个平行四边形,面积一定相等。
( )
(4)两个面积相等的平行四边形,底和高一定也分别相等。
( )
×
×
√
×
实战演练
填空。
(1)把一个平行四边形沿其中一条高剪开,平移后可以拼成一个( ),长方形的长就是平行四边形的( ),长方形的宽就是平行四边形的( )。
(2)一个平行四边形的周长为46cm,一边的长为14cm,另外三边的长分是( )、( )、( )。
(3)平行四边形的高是5cm,底是高的2倍,它的面积是( )cm 。
(4)填表(单位:cm)。
底 高 平行四边形的面积
0.7 50
8 9.6
0.02 6
实战演练
填空。
(1)把一个平行四边形沿其中一条高剪开,平移后可以拼成一个( ),长方形的长就是平行四边形的( ),长方形的宽就是平行四边形的( )。
(2)一个平行四边形的周长为46cm,一边的长为14cm,另外三边的长分是( )、( )、( )。
(3)平行四边形的高是5cm,底是高的2倍,它的面积是( )cm 。
(4)填表(单位:cm)。
底 高 平行四边形的面积
0.7 50 35
8 1.2 9.6
300 0.02 6
长方形
底
高
14cm
9cm
9cm
50
实战演练
有一块平行四边形草地,底长24m,高是底的一半。如果每平方米的草可供3只羊吃一天,这块草地可供多少只羊吃一天?
实战演练
有一块平行四边形草地,底长24m,高是底的一半。如果每平方米的草可供3只羊吃一天,这块草地可供多少只羊吃一天?
面积:S=24×(24÷2)=288(m )
288×3=864(只)
答:这块草地可供864只羊吃一天。
实战演练
用木条制成一个长方形的框架,长是18cm,宽是15cm,它的周长和面积各是多少?如果把它拉成平行四边形,那么周长和面积会发生怎么样的变化?
实战演练
用木条制成一个长方形的框架,长是18cm,宽是15cm,它的周长和面积各是多少?如果把它拉成平行四边形,那么周长和面积会发生怎么样的变化?
长方形的周长: (18+15)×2=66(cm)
长方形的面积:18×15=270(cm )
因为无论怎样变化周长总是四条边的和,所以周长不变。
平行四边形的面积是底乘以高,在变化过程中底是不变的,高是变化的,且高<长方形的宽,所以如果拉成平行四边形,面积会变小 。
2
0
2
2
Thanks for listening.
Welcome to ask questions
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
