北师大版九年级数学上册 4.3 相似多边形 教学课件(共18张PPT)
文档属性
| 名称 | 北师大版九年级数学上册 4.3 相似多边形 教学课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 605.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 12:06:09 | ||
图片预览




文档简介
(共18张PPT)
第四章 图形的相似
4.3 相似多边形
经历相似多边形概念的形成过程,了解相似多边形的含义;
进一步发展归纳、类比、反思、交流等方面的能力,提高数学思维水平,体会反例的作用.
学习目标
情境导入
A′
B′
C′
D′
E′
F′
A
B
C
D
E
F
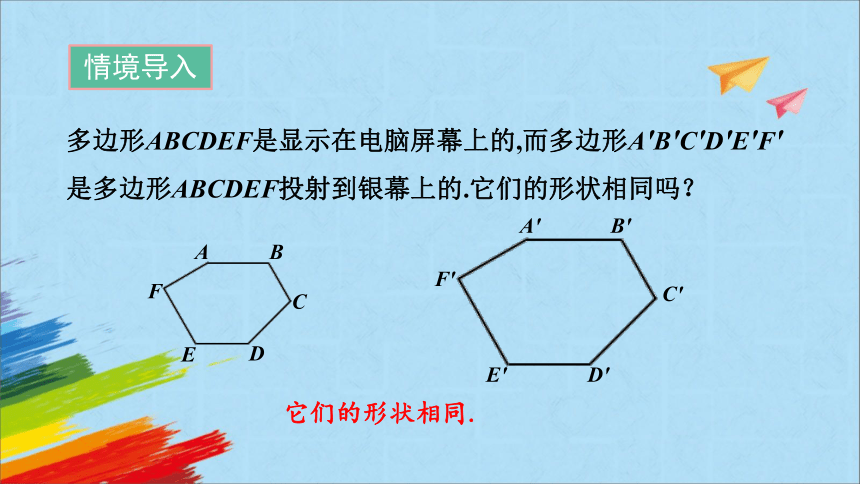
多边形ABCDEF是显示在电脑屏幕上的,而多边形A′B′C′D′E′F′是多边形ABCDEF投射到银幕上的.它们的形状相同吗?
它们的形状相同.
新课探究
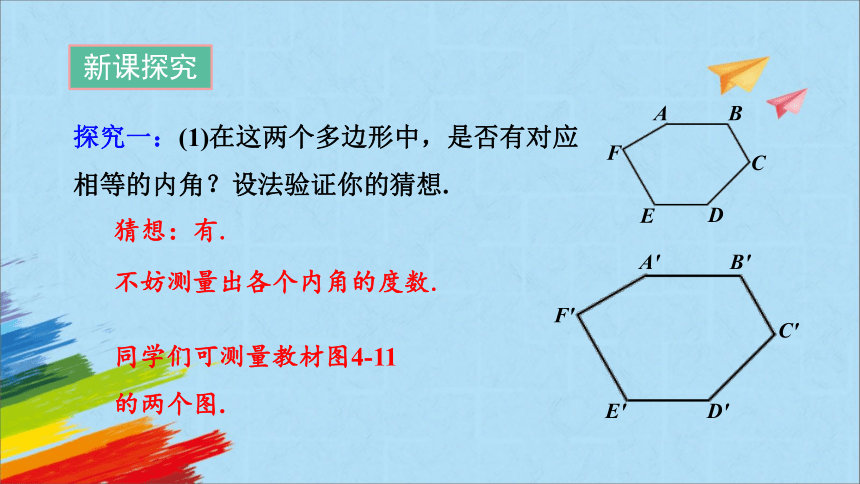
探究一:(1)在这两个多边形中,是否有对应相等的内角?设法验证你的猜想.
A′
B′
C′
D′
E′
F′
A
B
C
D
E
F
猜想:有.
不妨测量出各个内角的度数.
同学们可测量教材图4-11的两个图.
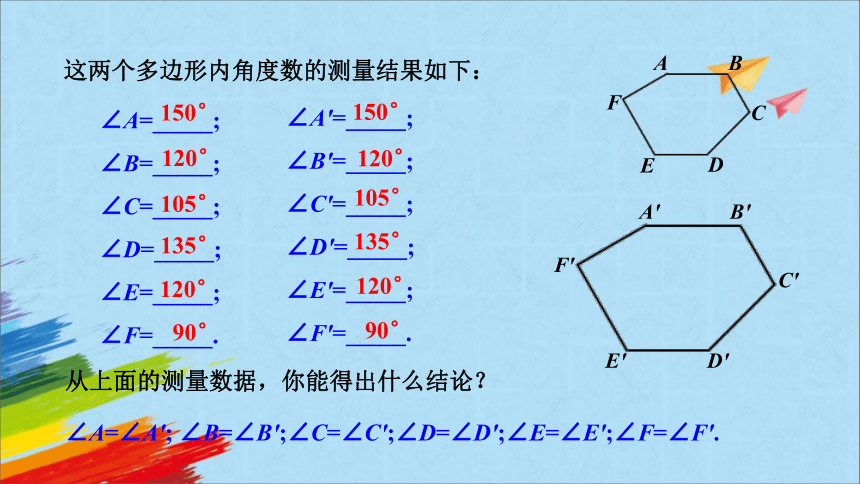
从上面的测量数据,你能得出什么结论?
∠A=∠A′; ∠B=∠B′;∠C=∠C′;∠D=∠D′;∠E=∠E′;∠F=∠F′.
∠A=_____;
∠B=_____;
∠C=_____;
∠D=_____;
∠E=_____;
∠F=_____.
∠A′=_____;
∠B′=_____;
∠C′=_____;
∠D′=_____;
∠E′=_____;
∠F′=_____.
120°
150°
150°
105°
120°
135°
105°
135°
120°
120°
90°
90°
这两个多边形内角度数的测量结果如下:
A′
B′
C′
D′
E′
F′
A
B
C
D
E
F
探究一:(2)在这两个多边形中,夹相等内角的两边否成比例?
仿照(1)中探究方法,通过测量并计算结果,给出结论.
结论:===== .
对应边
∠A=∠A′; ∠B=∠B′;∠C=∠C′;∠D=∠D′;∠E=∠E′;∠F=∠F′.
对应角
各角分别相等、各边成比例的两个多边形叫做相似多边形.
在探究一的图中,六边形ABCDEF与六边形A′B′C′D′E′F′相似,记作:六边形ABCDEF∽六边形A′B′C′D′E′F′.
“∽”读作:“相似于”.
相似多边形的性质
对应角相等
对应边成比例
注意:在记两个多边形相似时,要把表示对应顶点的字母写在对应的位置上.
如果五边形ABCDE∽五边形A′B′C′D′E′,对应边的比===== ,那么,
(1)五边形ABCDE与五边形A′B′C′D′E′的相似比k1=_______.
(2)五边形A′B′C′D′E′与五边形ABCDE的相似比k2=_______.
相似多边形对应边的比叫做相似比
①任意正三角形ABC与正三角形DEF:
B
C
D
E
F
A
探究二:(1)任意两个正三角形相似吗?任意两个正方形呢?任意两个正n边形呢?
由于正三角形每个角都等于60°,所以∠A=∠D= 60°,
∠B=∠E= 60°, ∠C=∠F= 60°;
由于正三角形三边都相等,所以
故任意两个正三角形相似.
②任意正方形ABCD与正方形EFGH:
B
C
D
E
F
A
H
G
由于正方形每个角都是直角,所以∠A=∠E= 90°, ∠B=∠F= 90°, ∠C=∠G= 90°, ∠D=∠H= 90°;
由于正方形四条边相等,所以
.
故任意两个正方形相似.
探究二:(2)任意两个菱形相似吗?
如右图所示的两个菱形,它们的各角不相等,因此不是相似图形.
即任意两个菱形不一定相似.
任意两个正n边形,它们形状相同,各角都相等,对应边成比例,因此它们是相似图形.
③任意两个正n 边形:
典型例题
【例1】如果两个多边形不相似,那么它们的各角可能对应相等吗?它们的各边可能对应成比例吗?
两个不相似的矩形,
各角相等.
两个不相似的菱形,
各边对应成比例.
【例2】一块长3m、宽1.5m的矩形黑板如图所示,镶在其外围的木质边框宽7.5cm,边框的内外边缘所成的矩形相似吗?为什么?
4.3 相似多边形
解:它们不相似,
因为 ≠,
所以对应边不成比例.
即这两个矩形不相似.
如图所示,在四边形ABCD中,AD∥BC,EF∥BC,EF将四边形ABCD分成两个相似四边形AEFD和EBCF. 若AD=3,BC=4,求AE∶EB的值.
解:∵四边形AEFD∽四边形EBCF,
∴ ,AE∶EB=AD∶EF.
∴EF2=AD·BC=3×4=12, ∴EF= .
∴AE∶EB=AD∶EF=3∶ = ∶2 .
延伸应用
课堂练习
1.下列命题中,正确的是( )
A.所有的等腰三角形都相似 B.所有的直角三角形都相似
C.所有的等边三角形都相似 D.所有的矩形都相似
C
2.若△ABC∽△A′B′C′,且AB∶A′B′=1∶2 .
则△ABC与△ A′B′C′相似比是 ,
△ A′B′C′与△ABC的相似比是 .
2
1∶2
3.下图中每组两个矩形相似吗?说说你的理由.
2
3
3
4.5
2
3
2.5
5
相似,
因为各角相等,
对应边成比例.
不相似,
因为对应边不成比例.
B
C
D
A
4.以正方形各边中点为顶点,可以组成一个新正方形,求新正方形与原正方形的相似比.
E
F
E、F分别是正方形ABCD的边AD、AB的中点,设正方形ABCD的边长为2,
则有:AE=AF=1,∠A=90°,那么
EF==. EF∶AB=∶2.
故新正方形与原正方形的相似比为∶2.
解:如图,
课堂小结
各角分别相等、各边成比例的两个多边形叫做相似多边形.
相似多边形的概念
相似多边形的性质
相似多边形的判定方法
相似多边形对应边的比叫做相似比.
第四章 图形的相似
4.3 相似多边形
经历相似多边形概念的形成过程,了解相似多边形的含义;
进一步发展归纳、类比、反思、交流等方面的能力,提高数学思维水平,体会反例的作用.
学习目标
情境导入
A′
B′
C′
D′
E′
F′
A
B
C
D
E
F
多边形ABCDEF是显示在电脑屏幕上的,而多边形A′B′C′D′E′F′是多边形ABCDEF投射到银幕上的.它们的形状相同吗?
它们的形状相同.
新课探究
探究一:(1)在这两个多边形中,是否有对应相等的内角?设法验证你的猜想.
A′
B′
C′
D′
E′
F′
A
B
C
D
E
F
猜想:有.
不妨测量出各个内角的度数.
同学们可测量教材图4-11的两个图.
从上面的测量数据,你能得出什么结论?
∠A=∠A′; ∠B=∠B′;∠C=∠C′;∠D=∠D′;∠E=∠E′;∠F=∠F′.
∠A=_____;
∠B=_____;
∠C=_____;
∠D=_____;
∠E=_____;
∠F=_____.
∠A′=_____;
∠B′=_____;
∠C′=_____;
∠D′=_____;
∠E′=_____;
∠F′=_____.
120°
150°
150°
105°
120°
135°
105°
135°
120°
120°
90°
90°
这两个多边形内角度数的测量结果如下:
A′
B′
C′
D′
E′
F′
A
B
C
D
E
F
探究一:(2)在这两个多边形中,夹相等内角的两边否成比例?
仿照(1)中探究方法,通过测量并计算结果,给出结论.
结论:===== .
对应边
∠A=∠A′; ∠B=∠B′;∠C=∠C′;∠D=∠D′;∠E=∠E′;∠F=∠F′.
对应角
各角分别相等、各边成比例的两个多边形叫做相似多边形.
在探究一的图中,六边形ABCDEF与六边形A′B′C′D′E′F′相似,记作:六边形ABCDEF∽六边形A′B′C′D′E′F′.
“∽”读作:“相似于”.
相似多边形的性质
对应角相等
对应边成比例
注意:在记两个多边形相似时,要把表示对应顶点的字母写在对应的位置上.
如果五边形ABCDE∽五边形A′B′C′D′E′,对应边的比===== ,那么,
(1)五边形ABCDE与五边形A′B′C′D′E′的相似比k1=_______.
(2)五边形A′B′C′D′E′与五边形ABCDE的相似比k2=_______.
相似多边形对应边的比叫做相似比
①任意正三角形ABC与正三角形DEF:
B
C
D
E
F
A
探究二:(1)任意两个正三角形相似吗?任意两个正方形呢?任意两个正n边形呢?
由于正三角形每个角都等于60°,所以∠A=∠D= 60°,
∠B=∠E= 60°, ∠C=∠F= 60°;
由于正三角形三边都相等,所以
故任意两个正三角形相似.
②任意正方形ABCD与正方形EFGH:
B
C
D
E
F
A
H
G
由于正方形每个角都是直角,所以∠A=∠E= 90°, ∠B=∠F= 90°, ∠C=∠G= 90°, ∠D=∠H= 90°;
由于正方形四条边相等,所以
.
故任意两个正方形相似.
探究二:(2)任意两个菱形相似吗?
如右图所示的两个菱形,它们的各角不相等,因此不是相似图形.
即任意两个菱形不一定相似.
任意两个正n边形,它们形状相同,各角都相等,对应边成比例,因此它们是相似图形.
③任意两个正n 边形:
典型例题
【例1】如果两个多边形不相似,那么它们的各角可能对应相等吗?它们的各边可能对应成比例吗?
两个不相似的矩形,
各角相等.
两个不相似的菱形,
各边对应成比例.
【例2】一块长3m、宽1.5m的矩形黑板如图所示,镶在其外围的木质边框宽7.5cm,边框的内外边缘所成的矩形相似吗?为什么?
4.3 相似多边形
解:它们不相似,
因为 ≠,
所以对应边不成比例.
即这两个矩形不相似.
如图所示,在四边形ABCD中,AD∥BC,EF∥BC,EF将四边形ABCD分成两个相似四边形AEFD和EBCF. 若AD=3,BC=4,求AE∶EB的值.
解:∵四边形AEFD∽四边形EBCF,
∴ ,AE∶EB=AD∶EF.
∴EF2=AD·BC=3×4=12, ∴EF= .
∴AE∶EB=AD∶EF=3∶ = ∶2 .
延伸应用
课堂练习
1.下列命题中,正确的是( )
A.所有的等腰三角形都相似 B.所有的直角三角形都相似
C.所有的等边三角形都相似 D.所有的矩形都相似
C
2.若△ABC∽△A′B′C′,且AB∶A′B′=1∶2 .
则△ABC与△ A′B′C′相似比是 ,
△ A′B′C′与△ABC的相似比是 .
2
1∶2
3.下图中每组两个矩形相似吗?说说你的理由.
2
3
3
4.5
2
3
2.5
5
相似,
因为各角相等,
对应边成比例.
不相似,
因为对应边不成比例.
B
C
D
A
4.以正方形各边中点为顶点,可以组成一个新正方形,求新正方形与原正方形的相似比.
E
F
E、F分别是正方形ABCD的边AD、AB的中点,设正方形ABCD的边长为2,
则有:AE=AF=1,∠A=90°,那么
EF==. EF∶AB=∶2.
故新正方形与原正方形的相似比为∶2.
解:如图,
课堂小结
各角分别相等、各边成比例的两个多边形叫做相似多边形.
相似多边形的概念
相似多边形的性质
相似多边形的判定方法
相似多边形对应边的比叫做相似比.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
