北师大版九年级数学上册 4.1 成比例线段 教学课件(共22张PPT)
文档属性
| 名称 | 北师大版九年级数学上册 4.1 成比例线段 教学课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 12:08:19 | ||
图片预览





文档简介
(共22张PPT)
第四章 图形的相似
4.1 成比例线段
结合现实情境感受学习线段的比的必要性,借助几何直观了解线段的比和成比例线段;
掌握比例的性质及其简单应用;
通过现实情境,进一步发展从数学角度发现问题、提出问题、解决问题的能力.
学习目标
新课导入
观察下面两组图片,你发现每组图片分别有什么共同点?
形状相同
形状相同
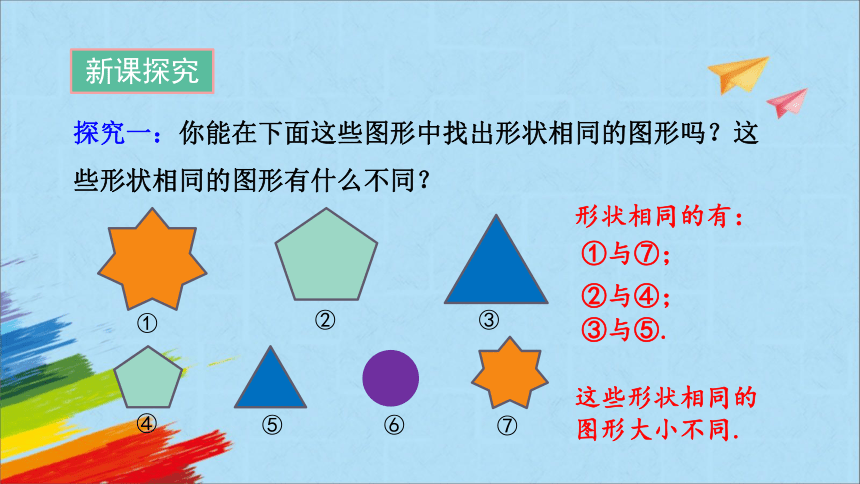
探究一:你能在下面这些图形中找出形状相同的图形吗?这些形状相同的图形有什么不同?
新课探究
①
②
③
④
⑤
⑥
⑦
形状相同的有:
①与⑦;
②与④;
③与⑤.
这些形状相同的图形大小不同.
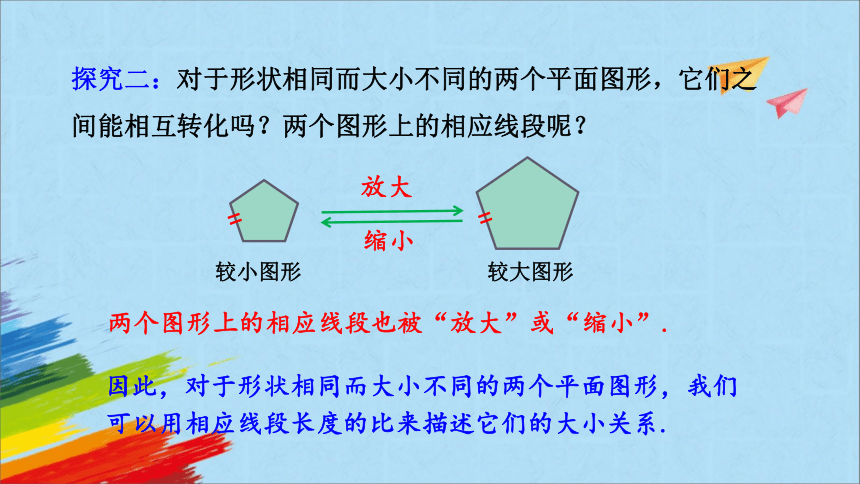
探究二:对于形状相同而大小不同的两个平面图形,它们之间能相互转化吗?两个图形上的相应线段呢?
放大
缩小
较小图形
较大图形
两个图形上的相应线段也被“放大”或“缩小”.
=
=
因此,对于形状相同而大小不同的两个平面图形,我们可以用相应线段长度的比来描述它们的大小关系.
知识点一:两条线段的比
如果选用同一个长度单位量得两条线段AB,CD的长度分别是m,n,那么这两条线段的比就是它们长度的比,
即AB∶ CD=m∶n,或写成= .
其中,线段AB,CD分别叫做这个线段比的前项和后项.
如果把表示成比值k,那么=k,或AB = k·CD.
两条线段的比实际上就是两个数(线段长度)的比.
形
数
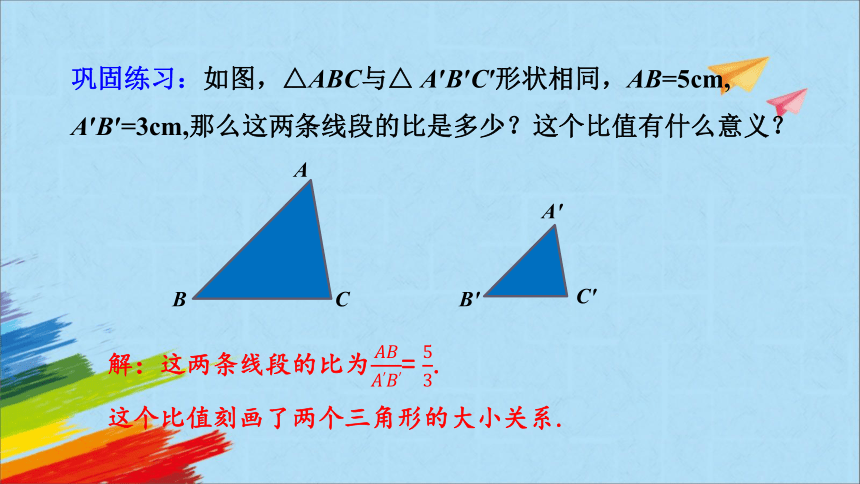
巩固练习:如图,△ABC与△ A′B′C′形状相同,AB=5cm, A′B′=3cm,那么这两条线段的比是多少?这个比值有什么意义?
A
B
C
A′
B′
C′
解:这两条线段的比为= .
这个比值刻画了两个三角形的大小关系.
探究三:如图,设小方格的边长为1,△ABC与△ A′B′C′的顶点都在格点上,(1) AB,BC,A′B′,B′C′的长度分别是多少?
A
B
C
A′
B′
C′
解:(1)由图可知,
AB==4,BC=6,
A′B′==2 B′C′=3.
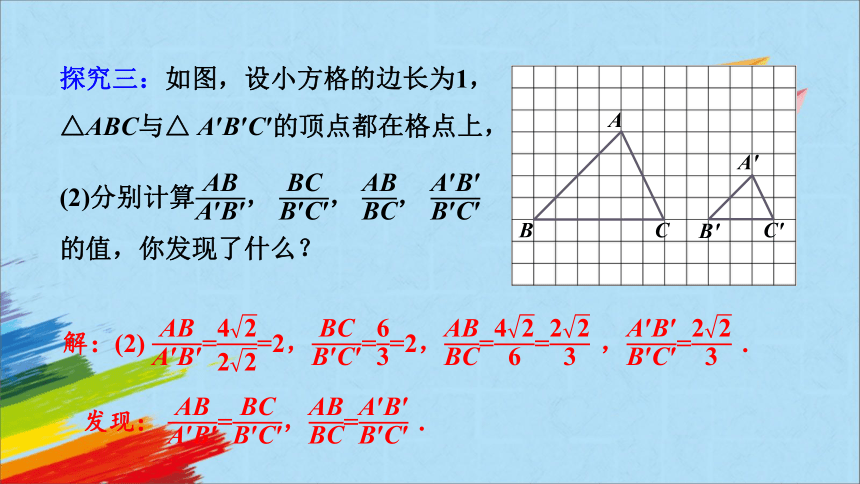
探究三:如图,设小方格的边长为1,△ABC与△ A′B′C′的顶点都在格点上,(2)分别计算, , , 的值,你发现了什么?
A
B
C
A′
B′
C′
解:(2) ==2,==2,==,=.
发现: =,=.
知识点二:成比例线段
四条线段a, b, c, d中, 如果a与b的比等于c与d的比, 即= , 那么这四条线段a, b, c, d叫做成比例线段, 简称比例线段.
探究三中的AB,BC,A′B′,B′C′是成比例线段吗?
AB,A′B′,BC,B′C′是成比例线段吗?
是
是
探究四:如果a, b, c, d四个数成比例,即=,那么ad=bc吗?
反过来,如果ad=bc ,那么a, b, c, d四个数成比例吗?
如果= ,那么ad=bc.
如果ad=bc(a, b, c, d 都不等于0),那么= .
解:在=的两边同时乘bd,可得ad=bc.
在ad=bc的两边同时除以bd,可得=.即a, b, c, d成比例.
比例的基本性质
探究五:(1)下图中,====2,你能求出的值吗?由此,你能得出什么结论?
A
B
C
D
H
E
F
G
分析:根据条件,用HE,EF,FG,HG分别表示AB, BC,
CD,AD,代入所求式子即可得到结果.
解:因为====2,
所以AB=2HE, BC=2EF, CD=2FG, AD=2HG.
所以=
==2.
结论:如果==k(b±d≠0),那么=k.
探究五: (2)已知a, b, c, d, e, f 六个数,如果==(b+d+f≠0),那么=成立吗?为什么?
解:设===k,那么a=kb,c=kd,e=kf.
===k=.
故=成立.
结论:如果==…=(b+d+…+n≠0),那么=.
等比性质
比例的基本性质
等比性质
有限
无限
扩充
典型例题
【例1】如图,一块矩形绸布的长AB=a m,宽AD=1m,按照图中所示的方式将它裁成相同的三面矩形彩旗,且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,即=,那么a的值应当是多少?
A
B
C
D
E
F
解:根据题意可知, AB=a m, AE=a m, AD=1m.
由 =,得 =,
即 a2=1
所以 a2=3.
开平方,得 a=(a=-舍去).
A
B
C
D
E
F
【例2】在△ABC与△DEF中,已知===,且△ABC的周长为18 cm,求△DEF的周长.
解:∵ ===.
∴ ==.
∴ =() ,
又∵ △ABC的周长为18 cm,即= 18 cm.
∴ =×18=24(cm),即△DEF的周长为24cm.
随堂检测
2.已知线段a=2cm,b=4.1cm,c=4cm,d=8.2cm,则有( )
A. d, b, a, c成比例线段 B. a, d, b, c成比例线段
C. a, c, b, d成比例线段 D. a, d, c, b成比例线段
1.下列各组线段的长度成比例的是( )
A.2cm,3cm,4cm,1cm B.1.5cm,2.5cm,6.5cm,4.5cm
C.1.1cm,2.2cm,3.3cm,4.4cm D.1cm,2cm,2cm,4cm
C
D
3.如图,在平行四边形ABCD中,∠B=30°,AD=10.AE为BC边上的高,垂足E为BC中点.求:AE∶BC.
B
A
E
C
D
解:在Rt△ABE中,
∵ ∠B=30°
∴ AB=2AE.
∵ BC=AD=10,E是BC中点,
∴ BE=5,由勾股定理可得
4.已知线段a=10mm , b=6cm, c=2cm , d=3cm .问:这四条线段是否成比例?为什么
解:这四条线段成比例.
∵ a=10mm=1cm,
∴ = , ==.
∴ =.
即线段a、c、d、b成比例.
课堂小结
成比例线段
成比例线段的概念
两条线段的比的概念
比例的基本性质
等比性质
叙述下面的相关概念及性质:
第四章 图形的相似
4.1 成比例线段
结合现实情境感受学习线段的比的必要性,借助几何直观了解线段的比和成比例线段;
掌握比例的性质及其简单应用;
通过现实情境,进一步发展从数学角度发现问题、提出问题、解决问题的能力.
学习目标
新课导入
观察下面两组图片,你发现每组图片分别有什么共同点?
形状相同
形状相同
探究一:你能在下面这些图形中找出形状相同的图形吗?这些形状相同的图形有什么不同?
新课探究
①
②
③
④
⑤
⑥
⑦
形状相同的有:
①与⑦;
②与④;
③与⑤.
这些形状相同的图形大小不同.
探究二:对于形状相同而大小不同的两个平面图形,它们之间能相互转化吗?两个图形上的相应线段呢?
放大
缩小
较小图形
较大图形
两个图形上的相应线段也被“放大”或“缩小”.
=
=
因此,对于形状相同而大小不同的两个平面图形,我们可以用相应线段长度的比来描述它们的大小关系.
知识点一:两条线段的比
如果选用同一个长度单位量得两条线段AB,CD的长度分别是m,n,那么这两条线段的比就是它们长度的比,
即AB∶ CD=m∶n,或写成= .
其中,线段AB,CD分别叫做这个线段比的前项和后项.
如果把表示成比值k,那么=k,或AB = k·CD.
两条线段的比实际上就是两个数(线段长度)的比.
形
数
巩固练习:如图,△ABC与△ A′B′C′形状相同,AB=5cm, A′B′=3cm,那么这两条线段的比是多少?这个比值有什么意义?
A
B
C
A′
B′
C′
解:这两条线段的比为= .
这个比值刻画了两个三角形的大小关系.
探究三:如图,设小方格的边长为1,△ABC与△ A′B′C′的顶点都在格点上,(1) AB,BC,A′B′,B′C′的长度分别是多少?
A
B
C
A′
B′
C′
解:(1)由图可知,
AB==4,BC=6,
A′B′==2 B′C′=3.
探究三:如图,设小方格的边长为1,△ABC与△ A′B′C′的顶点都在格点上,(2)分别计算, , , 的值,你发现了什么?
A
B
C
A′
B′
C′
解:(2) ==2,==2,==,=.
发现: =,=.
知识点二:成比例线段
四条线段a, b, c, d中, 如果a与b的比等于c与d的比, 即= , 那么这四条线段a, b, c, d叫做成比例线段, 简称比例线段.
探究三中的AB,BC,A′B′,B′C′是成比例线段吗?
AB,A′B′,BC,B′C′是成比例线段吗?
是
是
探究四:如果a, b, c, d四个数成比例,即=,那么ad=bc吗?
反过来,如果ad=bc ,那么a, b, c, d四个数成比例吗?
如果= ,那么ad=bc.
如果ad=bc(a, b, c, d 都不等于0),那么= .
解:在=的两边同时乘bd,可得ad=bc.
在ad=bc的两边同时除以bd,可得=.即a, b, c, d成比例.
比例的基本性质
探究五:(1)下图中,====2,你能求出的值吗?由此,你能得出什么结论?
A
B
C
D
H
E
F
G
分析:根据条件,用HE,EF,FG,HG分别表示AB, BC,
CD,AD,代入所求式子即可得到结果.
解:因为====2,
所以AB=2HE, BC=2EF, CD=2FG, AD=2HG.
所以=
==2.
结论:如果==k(b±d≠0),那么=k.
探究五: (2)已知a, b, c, d, e, f 六个数,如果==(b+d+f≠0),那么=成立吗?为什么?
解:设===k,那么a=kb,c=kd,e=kf.
===k=.
故=成立.
结论:如果==…=(b+d+…+n≠0),那么=.
等比性质
比例的基本性质
等比性质
有限
无限
扩充
典型例题
【例1】如图,一块矩形绸布的长AB=a m,宽AD=1m,按照图中所示的方式将它裁成相同的三面矩形彩旗,且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,即=,那么a的值应当是多少?
A
B
C
D
E
F
解:根据题意可知, AB=a m, AE=a m, AD=1m.
由 =,得 =,
即 a2=1
所以 a2=3.
开平方,得 a=(a=-舍去).
A
B
C
D
E
F
【例2】在△ABC与△DEF中,已知===,且△ABC的周长为18 cm,求△DEF的周长.
解:∵ ===.
∴ ==.
∴ =() ,
又∵ △ABC的周长为18 cm,即= 18 cm.
∴ =×18=24(cm),即△DEF的周长为24cm.
随堂检测
2.已知线段a=2cm,b=4.1cm,c=4cm,d=8.2cm,则有( )
A. d, b, a, c成比例线段 B. a, d, b, c成比例线段
C. a, c, b, d成比例线段 D. a, d, c, b成比例线段
1.下列各组线段的长度成比例的是( )
A.2cm,3cm,4cm,1cm B.1.5cm,2.5cm,6.5cm,4.5cm
C.1.1cm,2.2cm,3.3cm,4.4cm D.1cm,2cm,2cm,4cm
C
D
3.如图,在平行四边形ABCD中,∠B=30°,AD=10.AE为BC边上的高,垂足E为BC中点.求:AE∶BC.
B
A
E
C
D
解:在Rt△ABE中,
∵ ∠B=30°
∴ AB=2AE.
∵ BC=AD=10,E是BC中点,
∴ BE=5,由勾股定理可得
4.已知线段a=10mm , b=6cm, c=2cm , d=3cm .问:这四条线段是否成比例?为什么
解:这四条线段成比例.
∵ a=10mm=1cm,
∴ = , ==.
∴ =.
即线段a、c、d、b成比例.
课堂小结
成比例线段
成比例线段的概念
两条线段的比的概念
比例的基本性质
等比性质
叙述下面的相关概念及性质:
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
