北师大版九年级数学上册 4.4.1利用角判定三角形相似 教学课件(共14张PPT)
文档属性
| 名称 | 北师大版九年级数学上册 4.4.1利用角判定三角形相似 教学课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 661.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
4.4 探索三角形相似的条件
第1课时 利用角判定三角形相似
教学目标
掌握相似三角形的定义
经历两三角形相似条件的探索过程,掌握两三角形相似的判定条件:两角分别相等的两个三角形相似
能够运用三角形相似的条件解决简单的问题,进一步发展合情推理能力和初步的逻辑推理意识
回顾思考
相似多边形是如何定义的?
各角分别相等、各边成比例的两个多边形叫做相似多边形.
如果是相似三角形呢?
三角分别相等、三边成比例的两个三角形叫做相似三角形.
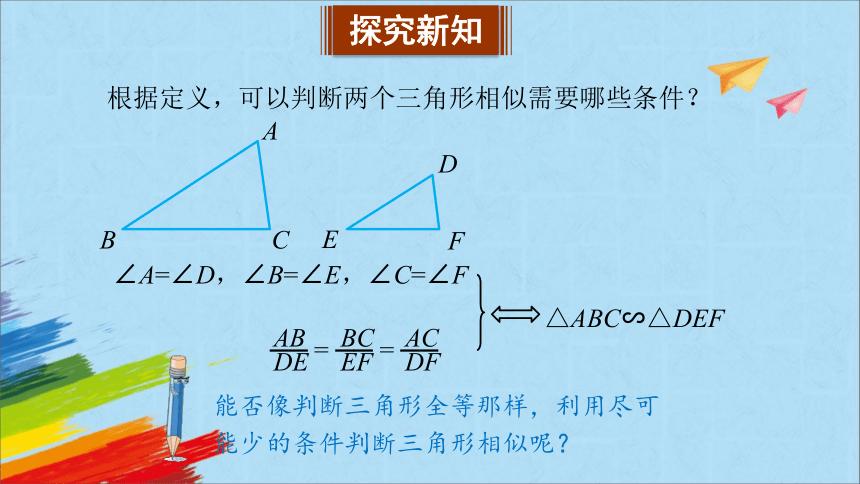
探究新知
∠A=∠D,∠B=∠E,∠C=∠F
── = ── = ──
AB
DE
BC
EF
AC
DF
△ABC∽△DEF
根据定义,可以判断两个三角形相似需要哪些条件?
能否像判断三角形全等那样,利用尽可能少的条件判断三角形相似呢?
A
B
C
D
E
F
两个三角形全等
判定方法
角边角(ASA)
角角边(AAS)
边边边(SSS)
边角边(SAS)
探究新知
对判定三角形相似是否适用呢?
全等三角形是相似三角形吗?
全等三角形是相似三角形,相似比是1.
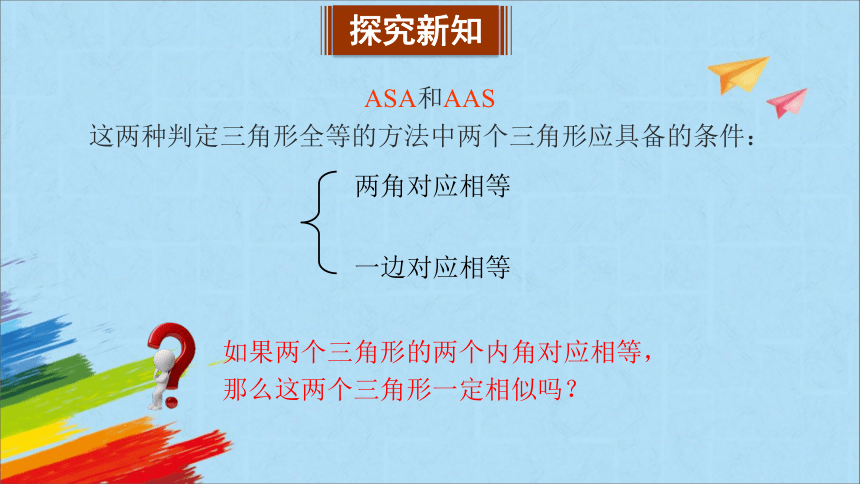
ASA和AAS
这两种判定三角形全等的方法中两个三角形应具备的条件:
两角对应相等
一边对应相等
如果两个三角形的两个内角对应相等,
那么这两个三角形一定相似吗?
探究新知
请依据下列条件画三角形:两人一组,一人画△ABC,另一人画△A1B1C1:
(1)使∠A=∠A1=45°,∠B=∠B1=30°;
(2)使∠A=∠A1=60°,∠B=∠B1=45°.
画完后,请解答下列问题:
① ∠C=∠C1吗?
② 先量出自己所画的三角形三边的长度,再合作求出对应边的比:、、(比值精确到0.1),它们相等吗?
③这两个三角形相似吗?
探究新知
定理 两角分别相等的两个三角形相似.
通过以上动手操作,我们有什么结论?
C
B1
B
C1
A
A1
探究新知
∠A=∠
∠B=∠
△ABC∽△A1B1C1
如果两个三角形有一个内角对应相等,那么这两
个三角形一定相似吗?能举例说明吗?
一角对应相等的两个三角形不一定相似.
探究新知
①
②
③
如图,三角形①与②、①与③、②与③均不相似.
课堂小结
________________________的两个三角形叫做相似三角形.
定理 _____________的两个三角形相似.
三角分别相等、三边成比例
两角分别相等
当堂检测
1.下列所给两个三角形不一定相似的是( )
A.两个等腰直角三角形
B.两个等边三角形
C.两个直角三角形
D.各有一个角是100°的两个等腰三角形
2.如图,点D,E分别在△ABC的边AB,AC上,
且∠1=∠2=∠B,则图中相似三角形有( )
A.1对 B.2对
C.3对 D.4对
C
D
3.如图,D是△ABC的边AB上一点,若∠1= ,则△ADC∽△ACB;若∠2= ,则△ADC∽△ACB.
∠B
∠ACB
当堂检测
4.如图,D是△ABC的边AB上一点,连接CD,若AD=2,BD=4,∠ACD=∠B,则AC的长为 .
2
当堂检测
5.如图,正方形ABCD中,点E,F,G分别在AB,BC,CD上,且∠EFG=90°.
求证:△EBF∽△FCG.
证明:∵四边形ABCD为正方形,
∴∠B=∠C=90°,
∴∠BEF+∠BFE=90°,
∵∠EFG=90°,
∴∠BFE+∠CFG=90°,
∴∠BEF=∠CFG,
∴△EBF∽△FCG.
感谢观看!
4.4 探索三角形相似的条件
第1课时 利用角判定三角形相似
教学目标
掌握相似三角形的定义
经历两三角形相似条件的探索过程,掌握两三角形相似的判定条件:两角分别相等的两个三角形相似
能够运用三角形相似的条件解决简单的问题,进一步发展合情推理能力和初步的逻辑推理意识
回顾思考
相似多边形是如何定义的?
各角分别相等、各边成比例的两个多边形叫做相似多边形.
如果是相似三角形呢?
三角分别相等、三边成比例的两个三角形叫做相似三角形.
探究新知
∠A=∠D,∠B=∠E,∠C=∠F
── = ── = ──
AB
DE
BC
EF
AC
DF
△ABC∽△DEF
根据定义,可以判断两个三角形相似需要哪些条件?
能否像判断三角形全等那样,利用尽可能少的条件判断三角形相似呢?
A
B
C
D
E
F
两个三角形全等
判定方法
角边角(ASA)
角角边(AAS)
边边边(SSS)
边角边(SAS)
探究新知
对判定三角形相似是否适用呢?
全等三角形是相似三角形吗?
全等三角形是相似三角形,相似比是1.
ASA和AAS
这两种判定三角形全等的方法中两个三角形应具备的条件:
两角对应相等
一边对应相等
如果两个三角形的两个内角对应相等,
那么这两个三角形一定相似吗?
探究新知
请依据下列条件画三角形:两人一组,一人画△ABC,另一人画△A1B1C1:
(1)使∠A=∠A1=45°,∠B=∠B1=30°;
(2)使∠A=∠A1=60°,∠B=∠B1=45°.
画完后,请解答下列问题:
① ∠C=∠C1吗?
② 先量出自己所画的三角形三边的长度,再合作求出对应边的比:、、(比值精确到0.1),它们相等吗?
③这两个三角形相似吗?
探究新知
定理 两角分别相等的两个三角形相似.
通过以上动手操作,我们有什么结论?
C
B1
B
C1
A
A1
探究新知
∠A=∠
∠B=∠
△ABC∽△A1B1C1
如果两个三角形有一个内角对应相等,那么这两
个三角形一定相似吗?能举例说明吗?
一角对应相等的两个三角形不一定相似.
探究新知
①
②
③
如图,三角形①与②、①与③、②与③均不相似.
课堂小结
________________________的两个三角形叫做相似三角形.
定理 _____________的两个三角形相似.
三角分别相等、三边成比例
两角分别相等
当堂检测
1.下列所给两个三角形不一定相似的是( )
A.两个等腰直角三角形
B.两个等边三角形
C.两个直角三角形
D.各有一个角是100°的两个等腰三角形
2.如图,点D,E分别在△ABC的边AB,AC上,
且∠1=∠2=∠B,则图中相似三角形有( )
A.1对 B.2对
C.3对 D.4对
C
D
3.如图,D是△ABC的边AB上一点,若∠1= ,则△ADC∽△ACB;若∠2= ,则△ADC∽△ACB.
∠B
∠ACB
当堂检测
4.如图,D是△ABC的边AB上一点,连接CD,若AD=2,BD=4,∠ACD=∠B,则AC的长为 .
2
当堂检测
5.如图,正方形ABCD中,点E,F,G分别在AB,BC,CD上,且∠EFG=90°.
求证:△EBF∽△FCG.
证明:∵四边形ABCD为正方形,
∴∠B=∠C=90°,
∴∠BEF+∠BFE=90°,
∵∠EFG=90°,
∴∠BFE+∠CFG=90°,
∴∠BEF=∠CFG,
∴△EBF∽△FCG.
感谢观看!
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
