北师大版九年级数学上册 6.3 反比例函数的应用 教学课件(共23张PPT)
文档属性
| 名称 | 北师大版九年级数学上册 6.3 反比例函数的应用 教学课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
第六章 反比例函数
6.3 反比例函数的应用
1.经历分析实际问题中两个变量之间的关系、建立反比例函数模型,进而解决问题的过程,进一步体会模型思想,发展应用意识.
2.能用反比例函数解决简单实际问题,进一步体会数形结合的思想,发展几何直观.
学习目标
1.反比例函数的图象与性质: 反比例函数y=的图象,当k>0时,图象位于第_________象限,在每一象限内,y的值随x值的___________;当k<0时,图象位于第_______象限,在每一象限内,y的值随x值的___________.
2.双曲线的两条分支逼近坐标轴但不可能与坐标轴相交.
3.反比例函数的图象是一个以_______为对称中心的中心对称图形.
复习回顾
一、三
增大而减小
二、四
增大而增大
原点
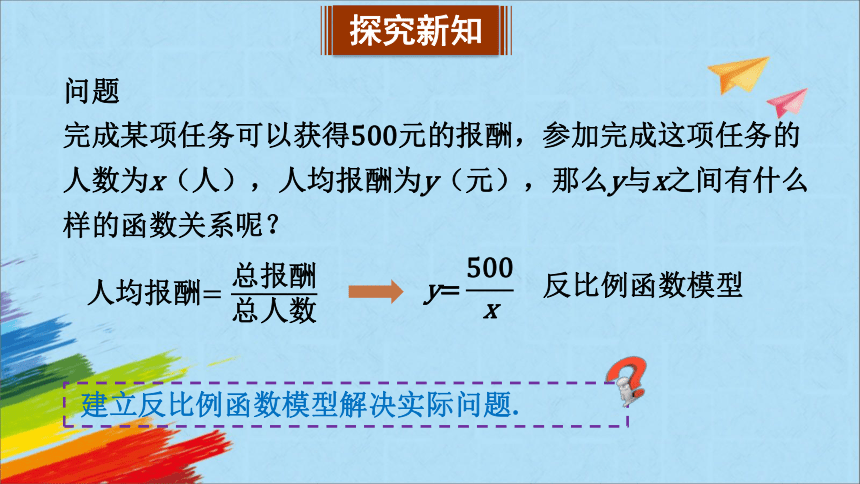
问题
完成某项任务可以获得元的报酬,参加完成这项任务的人数为(人),人均报酬为(元),那么与之间有什么样的函数关系呢?
人均报酬
建立反比例函数模型解决实际问题.
反比例函数模型
探究新知
(1)根据题目中的数量关系建立反比例函数模型,求出反比例函数的表达式;
(2)确定自变量的取值范围;
建立反比例函数模型解决实际问题的步骤:
(3)根据反比例函数的图象和性质解决问题.
【例1】某商场出售一批进价为2元的贺卡,在市场营销中发现,销售单价x元与日销售量y个之间有如下的关系:
(1)求y与x之间的关系式;
(2)设经营此卡的销售利润为w元,求w与x之间的关系式.若规定售价最高不能超过10元/个,求当日的销售单价定为多少时,才能获得最大日销售利润?
典例精讲
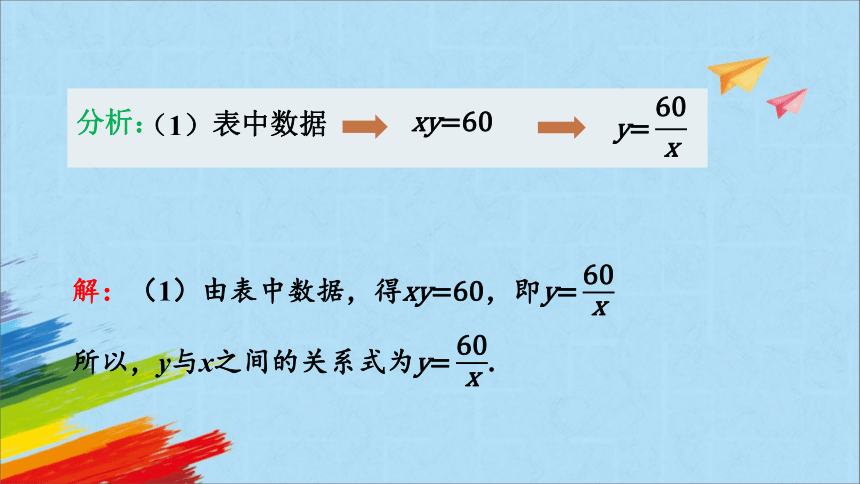
分析:
(1)
表中数据
解:(1)由表中数据,得,即
所以,y与x之间的关系式为.
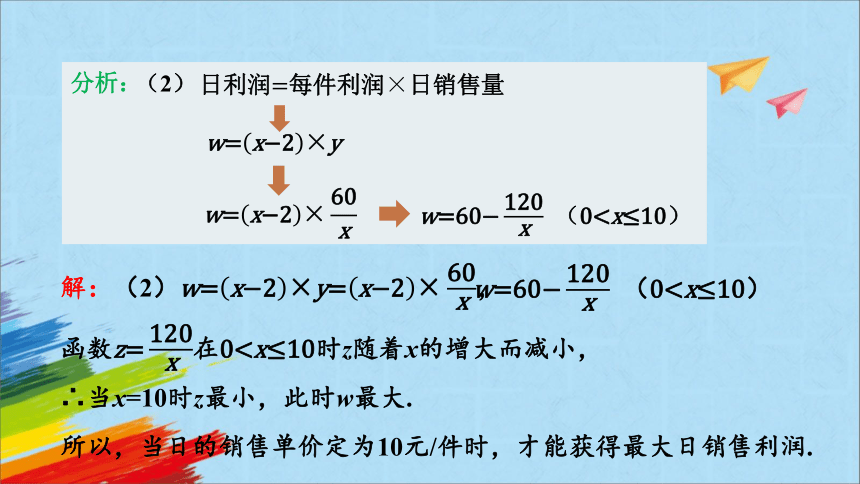
分析:
(2)
日利润每件利润日销售量
()
解:(2),
()
函数在时z随着x的增大而减小,
∴当x=10时z最小,此时w最大.
所以,当日的销售单价定为10元/件时,才能获得最大日销售利润.
【例2】如图是某一蓄水池每小时的排水量(m3/h)与排完蓄水池中的水所用的时间()之间的函数关系图象.
(1)写出此函数的表达式;
(2)如果要排完蓄水池中的水,那么
每小时的排水量应该是多少?
(3)如果每小时的排水量是5000m3,那么蓄水池中的水需要多长时间才能排完?
分析:
(1)
每小时的排水量排完水的时间总蓄水量
解:(1)由图象信息可知,当每小时的排水量为4000m3时,排完蓄水池中的水需要12 h.
所以蓄水池中蓄水量为4000×12=48000(m3)
所以 .
所以函数的解析式为 ().
分析:
(2)
求出当时,的值即可.
解:
(2)
当时,.
所以如果要排完蓄水池中的水,那么每小时的排水量应该是.
分析:
(3)
求出当时,的值即可.
解:
(3)
当时,.
所以如果每小时的排水量是,那么蓄水池中的水需要才能排完.
【例3】如图为某人对地面的压强(单位:N/m2)与这个人和地面接触面积(单位:m2)的函数关系图象.
(1)通过图象确定这个人的体重;
(2)如果此人所穿的每只鞋与地面的接触面积大约是cm2,那么此人双脚站立时对地面的压强是多少?
(3)如果某一沼泽地面能承受的最大
压强为300 N/m2 ,那么此人应站立在
面积至少多大的木板上才不至于下陷
(木板质量不计)?
分析:压强的计算公式是:p=.
当人和木板对湿地的压力一定时,随着面积 S(m )的不断增大,人对地面的压强 p( N/m2 )将不断减小.
解:
(1)
由图象知,,
所以,.
所以,.
所以,这个人的体重约61kg.
(2)
×10-2,
所以,.
所以,此人双脚站立时对地面的压强是
(3)
当时,
所以,此人应站立在至少2平方米的木板上才不至于下陷.
解:
1.某超市出售一批休闲鞋,进价为元双,经过一段时间的销售发现,日销量(双)是售价(元双)的反比例函数,且当售价为元双时,每日可售出双.
(1)求与之间的关系式;
(2)若超市计划日销售利润为元,则售价应定为多少?
随堂练习
把,代入上式,得,
解得.
解:
设().
(1)
所以与之间的关系式为().
解:(2)
由题意,得(),
即().
解得.
所以售价应定为元.
2.某厂从2016年起开始投入技术改进资金,改进后,其产品生产成本不断降低,具体数据如下表:
(1)根据表中的数据,确定你学过的哪种函数能表示其变化规律,说明确定这种函数的理由,并求出表达式;
(2)按照这种规律,若从2020年投入资金万元.
①预计生产成本比2019年降低多少万元?
②若打算在年把每件的成本降低到万元,则还需要投入资金多少万元?
年度 2016 2017 2018 2019
投入资金(万元) 2.5 3 4 4.5
产品成本(万元/件) 7.2 6 4.5 4
解:
(1)
由表中数据知,
反比例函数.
理由为:
所以,.
(2)①当万元时,.
∵(万元).
∴生产成本比2019年降低了(万元).
②当时,.
∴.
(万元).
所以,还需要投入资金0.625万元.
3.气球内充满一定质量的气体,当温度不变时,气球内的气压(千帕)是气球体积(米3)的反比例函数,其图象如图所示.
(1)写出这个函数的表达式;
(2)当气体的体积为m3时,气球内的气压是多少千帕?
(3)当气球内的气压大于千帕时,气球将爆炸,
为了安全起见,气球的体积应不小于多少?
解:
(1)
设,
所以,.
所以,
(2)
当,
所以,当气体的体积为m3时,气球内的气压是120千帕.
(3)
当千帕时,
函数,随着的减小而增大,
所以气球的体积应不小于m3.
(1)根据题目中的数量关系建立反比例函数模型,求出反比例函数的表达式;
(2)确定自变量的取值范围;
建立反比例函数模型解决实际问题的步骤:
(3)根据反比例函数的图象和性质解决问题.
课堂小结
再见
第六章 反比例函数
6.3 反比例函数的应用
1.经历分析实际问题中两个变量之间的关系、建立反比例函数模型,进而解决问题的过程,进一步体会模型思想,发展应用意识.
2.能用反比例函数解决简单实际问题,进一步体会数形结合的思想,发展几何直观.
学习目标
1.反比例函数的图象与性质: 反比例函数y=的图象,当k>0时,图象位于第_________象限,在每一象限内,y的值随x值的___________;当k<0时,图象位于第_______象限,在每一象限内,y的值随x值的___________.
2.双曲线的两条分支逼近坐标轴但不可能与坐标轴相交.
3.反比例函数的图象是一个以_______为对称中心的中心对称图形.
复习回顾
一、三
增大而减小
二、四
增大而增大
原点
问题
完成某项任务可以获得元的报酬,参加完成这项任务的人数为(人),人均报酬为(元),那么与之间有什么样的函数关系呢?
人均报酬
建立反比例函数模型解决实际问题.
反比例函数模型
探究新知
(1)根据题目中的数量关系建立反比例函数模型,求出反比例函数的表达式;
(2)确定自变量的取值范围;
建立反比例函数模型解决实际问题的步骤:
(3)根据反比例函数的图象和性质解决问题.
【例1】某商场出售一批进价为2元的贺卡,在市场营销中发现,销售单价x元与日销售量y个之间有如下的关系:
(1)求y与x之间的关系式;
(2)设经营此卡的销售利润为w元,求w与x之间的关系式.若规定售价最高不能超过10元/个,求当日的销售单价定为多少时,才能获得最大日销售利润?
典例精讲
分析:
(1)
表中数据
解:(1)由表中数据,得,即
所以,y与x之间的关系式为.
分析:
(2)
日利润每件利润日销售量
()
解:(2),
()
函数在时z随着x的增大而减小,
∴当x=10时z最小,此时w最大.
所以,当日的销售单价定为10元/件时,才能获得最大日销售利润.
【例2】如图是某一蓄水池每小时的排水量(m3/h)与排完蓄水池中的水所用的时间()之间的函数关系图象.
(1)写出此函数的表达式;
(2)如果要排完蓄水池中的水,那么
每小时的排水量应该是多少?
(3)如果每小时的排水量是5000m3,那么蓄水池中的水需要多长时间才能排完?
分析:
(1)
每小时的排水量排完水的时间总蓄水量
解:(1)由图象信息可知,当每小时的排水量为4000m3时,排完蓄水池中的水需要12 h.
所以蓄水池中蓄水量为4000×12=48000(m3)
所以 .
所以函数的解析式为 ().
分析:
(2)
求出当时,的值即可.
解:
(2)
当时,.
所以如果要排完蓄水池中的水,那么每小时的排水量应该是.
分析:
(3)
求出当时,的值即可.
解:
(3)
当时,.
所以如果每小时的排水量是,那么蓄水池中的水需要才能排完.
【例3】如图为某人对地面的压强(单位:N/m2)与这个人和地面接触面积(单位:m2)的函数关系图象.
(1)通过图象确定这个人的体重;
(2)如果此人所穿的每只鞋与地面的接触面积大约是cm2,那么此人双脚站立时对地面的压强是多少?
(3)如果某一沼泽地面能承受的最大
压强为300 N/m2 ,那么此人应站立在
面积至少多大的木板上才不至于下陷
(木板质量不计)?
分析:压强的计算公式是:p=.
当人和木板对湿地的压力一定时,随着面积 S(m )的不断增大,人对地面的压强 p( N/m2 )将不断减小.
解:
(1)
由图象知,,
所以,.
所以,.
所以,这个人的体重约61kg.
(2)
×10-2,
所以,.
所以,此人双脚站立时对地面的压强是
(3)
当时,
所以,此人应站立在至少2平方米的木板上才不至于下陷.
解:
1.某超市出售一批休闲鞋,进价为元双,经过一段时间的销售发现,日销量(双)是售价(元双)的反比例函数,且当售价为元双时,每日可售出双.
(1)求与之间的关系式;
(2)若超市计划日销售利润为元,则售价应定为多少?
随堂练习
把,代入上式,得,
解得.
解:
设().
(1)
所以与之间的关系式为().
解:(2)
由题意,得(),
即().
解得.
所以售价应定为元.
2.某厂从2016年起开始投入技术改进资金,改进后,其产品生产成本不断降低,具体数据如下表:
(1)根据表中的数据,确定你学过的哪种函数能表示其变化规律,说明确定这种函数的理由,并求出表达式;
(2)按照这种规律,若从2020年投入资金万元.
①预计生产成本比2019年降低多少万元?
②若打算在年把每件的成本降低到万元,则还需要投入资金多少万元?
年度 2016 2017 2018 2019
投入资金(万元) 2.5 3 4 4.5
产品成本(万元/件) 7.2 6 4.5 4
解:
(1)
由表中数据知,
反比例函数.
理由为:
所以,.
(2)①当万元时,.
∵(万元).
∴生产成本比2019年降低了(万元).
②当时,.
∴.
(万元).
所以,还需要投入资金0.625万元.
3.气球内充满一定质量的气体,当温度不变时,气球内的气压(千帕)是气球体积(米3)的反比例函数,其图象如图所示.
(1)写出这个函数的表达式;
(2)当气体的体积为m3时,气球内的气压是多少千帕?
(3)当气球内的气压大于千帕时,气球将爆炸,
为了安全起见,气球的体积应不小于多少?
解:
(1)
设,
所以,.
所以,
(2)
当,
所以,当气体的体积为m3时,气球内的气压是120千帕.
(3)
当千帕时,
函数,随着的减小而增大,
所以气球的体积应不小于m3.
(1)根据题目中的数量关系建立反比例函数模型,求出反比例函数的表达式;
(2)确定自变量的取值范围;
建立反比例函数模型解决实际问题的步骤:
(3)根据反比例函数的图象和性质解决问题.
课堂小结
再见
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
