总复习知识梳理(课件)苏教版五年级上册数学(共51张PPT)
文档属性
| 名称 | 总复习知识梳理(课件)苏教版五年级上册数学(共51张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 00:00:00 | ||
图片预览











文档简介
(共51张PPT)
知识点:
一、正、负数的含义和读、写方法
二、用正负数表示生活中具有相反意义的量
一、负数的初步认识
知识点一
正、负数的含义和读、写方法
1.认识测量温度的单位,认识温度计,认识测量温度的单位(摄氏度℃、华氏度℉)
2.正、负数的读写方法
①写正数时,“+”正号可以写上,也可以省略。
读的时候带“+”正号的要读出来,不带“+”正号的省略不读。
②写负数时,“-”负号不能省略,读的时候也要读出来。
注:0既不是正数,也不是负数。它是正数和负数的分界点。
知识点二
用正负数表示生活中具有相反意义的量
①表示盈亏情况 盈利——亏损
②表示向相反方向行走的路程 向东——向西 向南——向北
……
③借助直线上的点体会正、负数的大小。
(1)“0”表示学校所在的位置,“2”表示邮局所在的位置,“-2”表示公园所在的位置。
(2) 在0的右边,向右等距离地标有1、2......各点,在0的左边,向左等距离地标有 -1、- 2......各点。
(3) 对应的正、负数到0的距离相等。如 - 2到0是2个等距离长度,2到0也是2个等距离长度。
知识点二
用正负数表示生活中具有相反意义的量
知识点:
一、平行四边形面积的计算
二、三角形面积的计算
三、梯形面积的计算
四、公顷和平方千米
五、组合图形和不规则图形的面积
二、多边形的面积
知识点一
平行四边形面积的计算
求平行四边形的面积时,底和高要对应。
平行四边形的面积=底×高 S=ah
平行四边形的底=面积÷高 a=S÷h
平行四边形的高=面积÷底 h=S÷a
知识点二
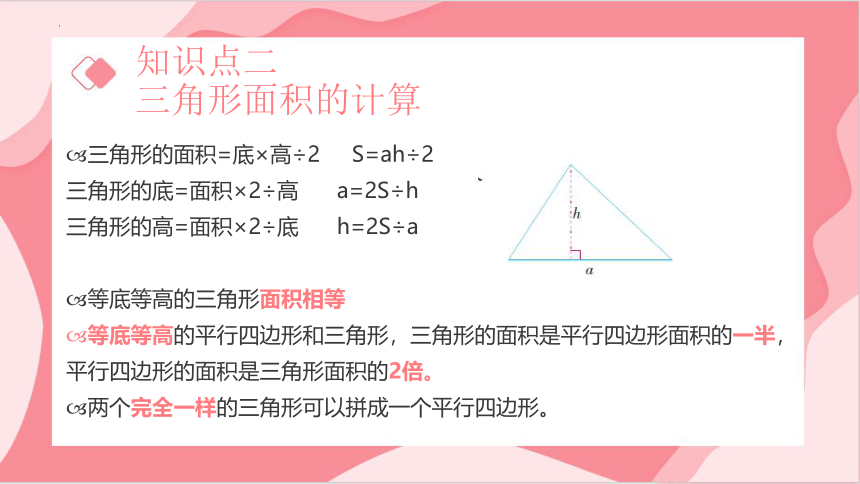
三角形面积的计算
三角形的面积=底×高÷2 S=ah÷2
三角形的底=面积×2÷高 a=2S÷h
三角形的高=面积×2÷底 h=2S÷a
等底等高的三角形面积相等
等底等高的平行四边形和三角形,三角形的面积是平行四边形面积的一半,平行四边形的面积是三角形面积的2倍。
两个完全一样的三角形可以拼成一个平行四边形。
知识点三
梯形面积的计算
梯形的面积=(上底+下底)×高÷2
S=(+b)×h÷2
两个完全相同的梯形可以拼成一个平行四边形
等高等面积的三角形和梯形,三角形的底等于梯形的上、下底之和。
1、边长是100米的正方形面积是1公顷。即1公顷=10000平方米
2、边长是1000米的正方形面积是1平方千米。平方千米有时也称平方公里。
即1平方千米=100公顷=1000000平方千米
知识点四
公顷和平方千米
知识点五
组合图形和不规则图形的面积
组合图形是由几个简单的图形组合而成的,其面积及可以看作几个简单图形的面积和,也可以看作几个简单图形的面积差。
计算组合图形的方法:
分割求和 添补求差
注:在对组合图形进行分割时,一定要考虑到分别求面积时所需要的数据条件是否充分。
计算不规则图形
1.数方格法 整格数+半格数÷2
知识点:
一、小数的意义和读、写方法
二、小数的性质和大小比较
三、大数目的改写
四、小数的近似数
三、小数的意义和性质
知识点一
小数的意义和读、写方法
1.小数的意义
分母是10.100.1000……的分数都可以用小数表示。
一位小数表示十分之几,;两位小数表示百分之几,三位小数表示千分之几...
2.小数的写法
写小数时,小数点写在个位的右下角,小数部分顺次写出每个数位上的数字。
eg: 0.01 0.04
3.小数的读法: 整数部分按整数的读法来读,小数点读作“点”,小数部分顺次读出每个数位上的数字。
eg: 0.01读作零点零一 0.04读作零点零四
知识点一
小数的意义和读、写方法
计数单位
小数点右边第一位是十分位,计数单位是 (0.1)
小数点右边第二位是百分位,计数单位是(0.01)
小数点右边第三位是千分位,计数单位是 (0.001)
小数中每相邻两个计数单位的进率都是10。
知识点二
小数的性质和大小比较
小数的性质
在小数的末尾添上“0”或去掉“0”,小数的大小不变。
根据小数的性质,通常可以去掉小数末尾的0,把小数化简。(
小数中间的0不能去)
小数的大小比较
知识点三
大数目的改写
把较大的数改写成用万做单位的小数分两步:一点二添
1点:先在这个数万位右下角点上小数点
2添:再在数的末尾填写万字
注:先分级
如果小数的未尾有0,那么不要忘了化简。
eg: 把384400改写成用万做单位的数
解析: 38.44万
如果已知数不够一万,那么整数部分要用0来占位。
如: 3350=0.335万
知识点三
大数目的改写
把较大的数改写成用万或亿做单位的小数分两步:一点二添
1点:先在这个数万位或者亿位右下角点上小数点
2添:再在数的末尾填写万字或亿字
注:先分级,四位数一级,再点小数点。
如果小数的未尾有0,那么不要忘了化简。
eg: 把384400改写成用万做单位的数 解析: 38.44万
如果已知数不够一万,那么整数部分要用0来占位。 如: 3350=0.335万
eg:把149600000改写成用亿做单位的数 解析: 1.496亿。
如果末尾有0 ,要记得化简。
知识点四
小数的近似数
求一个数的近似数的方法与求整数的近似数的方法相似,
根据要求用“四舍五入”法保留一定的小数位数。
eg: 地球和太阳之间的平均距离大约是1.496亿千米,
你知道:(1)精确到十分位大约是多少亿千米
(2) 精确到百分位大约是多少亿千米
解析:精确到十分位: 1.496亿千米≈1.5亿千米
精确到百分位: 1.496亿千米≈1.50亿千米
注:
把一个数精确到某一位,就是求这个数保留一定小数后的近似数。
知识点:
一、笔算小数加法和减法
二、用计算器计算小数加法和减法
四、小数的加法和减法
知识点一
笔算小数加法和减法
计算方法:
先把各数的小数点对齐
再按照整数加、减法的计算方法进行计算
得数里的小数点要与横线上的小数点对齐
计算结果能化简的要化简
知识点一
用计算器计算小数加法和减法
1)要按照从左到右的顺序依次按出每一个数字和运算符号:
2)如果一个小数整数部分是“0”,那么这个0可以省略不按,直接按小数点键,再依次按出小数部分的每一个数字的数字键;
(3如果一个小数的小数部分未尾有0,这个0也可以省略不按。
知识点:
一、小数乘整数
二、除数是整数的小数除法
三、小数乘小数、积的近似值
四、一个数除以小数
五、商的近似值
六、小数四则混合运算
五、小数的乘法和除法
知识点一
小数乘整数
1.小数乘整数的计算方法
①按照整数乘法计算
②因数中一共有几位小数,就从积的右边起数出几位,点上小数点
③如果积的小数位数不够,要在前面用0补位,再点上小数点;
④积的小数部分末尾的0要去掉
用竖式计算时,如果积的末尾有0
一定要先点积中的小数点
再去掉小数部分末尾的0。
知识点一
小数乘整数 小数点向右移动的变化规律
5.04×10=50.4
5.04×100=504
5.04×1000=5040
一个小数乘10、100、1000……只要把这个数的小数点向右移动一位、两位、三位……
积的变化规律
两个数相乘,
一个因数扩大(或缩小)m倍,另一个因数不变,那么它们的积也扩大 (或缩小) m倍(m≠0)。
一个因数扩大m倍,一个因数扩大n倍,积就扩大m×n倍。
两个数相乘,一个因数扩大了n倍,另一个因数缩小到原来的,那么它们的积不变。
知识点二
除数是整数的小数除法
1.小数除以整数的计算方法:
①按照整数除法的计算方法计算,商的小数点要和被除数的小数点对齐。
②如果除到被除数的未位仍有余数,要在余数后面添0继续除。
③如果小数的整数部分不够除,在商的个位上商0占位,对齐被除数的小数点,点上商的小数点,再继续除。
注:除到哪一位不够除时,
要在商的那一位上商0占位,
然后继续除。
知识点二
除数是整数的小数除法
小数点向左移动的变化规律
21.5÷10=2.15
21.5÷100=0.215
21.5÷1000=0.0215
小数点向左移动引起小数大小的变化规律:
一个数除以10、100、1000……只要把这个小数点向左移动一位、两位、三位······
差倍问题
已知两个数的差及它们的倍数关系,求这两个数的问题就是差倍问题
在差倍问题中,
小数=差÷ (倍数一1)
大数=差+小数或大数=小数X倍数
例:一个小数,如果把小数点向右移动一位,所得的数比原来增加63.72,这个小数是多少
解析:
把一个小数的小数点向右移动一位,所得的数就扩大到原来的10倍,即所得的数比原来增加了10-1 = 9倍,已知所得的数比原来增加了63.72,说明原数的(10-1) 倍正好是63.72,求原数是多少,用除法计算。
10-1=9 63.72÷9=7.08
商的变化规律
商的变化规律:
被除数不变,除数扩大(或缩小)多少倍,商就缩小或(扩大)多少倍
除数不变,被除数扩大(或缩小)多少倍,商就扩大(或缩小)多少倍
被除数和除数同时乘或除以一个相同的数(0除外),商不变
知识点三
小数乘小数
①按照整数乘法的计算方法算出积
②看因数中一共有几位小数,就从积的右边起数出几位,点上小数点
③积的小数位数如果不够,要先在前面用 0 补位,再点上小数点
④积的小数部分未尾有0,要根据小数的性质去掉。
知识点三
小数乘小数 积的大小与因数的关系
①一个数(0除外) 乘大于1的数,积大于原来的数;
②一个数(0除外) 乘小于1的数,积小于原来的数;
③一个数 (0除外) 乘1,积等于原来的数。
知识点三
小数乘小数 积的近似值
求积的近似值,要先算出积,再看需要保留位数的后一位上的数字,最后按照“四舍五入”法求出结果,并用“≈”连接。
知识点四
一个数除以小数
一个数除以小数的计算方法:
①先移动除数的小数点,使它变成整数
②除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数的未尾用0补足)
③然后按除数是整数的小数除法进行计算
注:除数是小数的除法,商的小数点应与被除数移动后的小数点对齐,与移动前的小数点无关。
知识点四
一个数除以小数 商与被除数的大小关系
①一个数(0除外) 除以大于1的数,商小于原来的数;
②一个数(0除外) 除以小于1的数,商大于原来的数;
③一个数 (0除外) 除以1,商等于原来的数。
知识点五
商的近似值 四舍五入法
用四舍五入法求商的近似值
求商的近似值,一般先算出比需要保留的小数位数多一位的商,
再按照“四舍五人”法写出结果。
5.713÷3≈1.90(保留两位小数)
注求商的近似数时,有时保留指定小数位数后,近似数的末尾有0,此时0不能去掉。
知识点五 循环小数
注:循环小数一定是无限小数,无限小数不一定是循环小数
知识点五
商的近似值 用“进一法”或“去尾法”解决问题
在解决实际问题时,取商的近似值可以根据具体的情况采用进一法或去尾法。
注:现实生活中,求最多能做多少套衣服、最多能买多少本书等问题,应采用去尾法。
注现实生活中,求至少需要几辆车才能运完,至少需要几个箱子才能装下等问题,应采用进一法。
知识点六 小数四则混合运算
1.小数的四则混合运算:
(1)小数四则混合运算和整数四则混合运算的运算顺序相同:
在没有括号的算式里,如果只有加减法或乘除法,要从左到右依次计算;
如果既有加减法,又有乘除法,要先算乘除法,后算加减法。
有括号,要先算括号里面的,再算括号外面的。
知识点六 小数四则混合运算
整数运算定律在小数中的应用
①整数加法的运算定律、减法的运算性质对小数加减法同样适用
②整数乘法的交换律、结合律和分配律、除法的运算性质对小数乘除法同样适用
(3)应用运算定律可以使一些计算简便。
知识点:
一、复式统计表
二、复式条形统计图(二)
六、统计表和条形统计图(二)
知识点一 复式统计表
1、复式统计表能把两个 (或多个) 统计内容 (单式统计表)的数据合并在一张表上。
2、特点: 第一栏左上角一般为表头意横栏中各个数据的和用合计表示 ,竖栏中各个数据的和用总计表示。
注:
复式统计表的优点: 不仅能反映每个类别的数据情况,更能从整体上反映所有类别的数据情况。
知识点一 复式统计表
填写复式统计表的方法与填写单式统计表的方法基本相同.
需要计算出合计数和总计数
①填写表头:确定横栏与竖栏表示的内容
②填入每组别对应的数据,并计算“合计数”“总计”;
③填写标题和制表日期。
知识点二 复式条形统计图(二)
1、定义:在同一幅条形统计图中,用两种 (或多种) 不同的直条描述两组 (或多组)不同的数据,这样的统计图叫做复式条形统计图。
2、特点: 不但可以清楚地表示出各种数量的多少,而且能直观、形象地比较两种或多种数量之间的关系。
①写出标题和制图日期
②确定横轴和纵轴:注明所代表的事物
③横轴:直条的宽度和间隔纵轴:确定单位长度
④根据数据画出相应的直条
⑤标明图例,涂上不同的颜色 (或底纹)
注:在绘制复式条形统计图时,一定要画出图例,条形的宽度要一致,间隔要相等,单位长度要统一。
知识点:
用列举的策略解决问题
七、解决问题的策略
用列举的策略解决问题
用列举的策略解决问题时:
要先按一定的顺序将所有的情况列举出来
再从中找出符合要求的答案
eg: 4个朋友见面,每两人握手,一共要握___6___次手。
注:列举时不能杂乱无章地罗列,要按一定的顺序,这样才能做到不重复.不遗漏。
知识点:
一、用含有字母的式子表示简单的数量关系。
二、用含有字母的式子表示稍复杂的数量关系和公式。
三、化简含有字母的式子。
八、用字母表示数
知识点一
用含有字母的式子表示简单的数量关系。
1.用字母可以表示数,用含有字母的式子可以表示数量关系。
2.当字母的值确定时,含有字母的式子的值也随之确定。
注:
①在含有字母的式子里,字母的值要符合实际情况
②当数与字母相乘时,中间的乘号可以省略不写,省略乘号时,一般把数写在字母的前面(只有×可以省略)
例:x×8a=8x
③如果字母与1相乘,可以省略1与乘号。
例:1×n=n
知识点二
用含有字母的式子表示稍复杂的数量关系。
根据题意,找出题目中的数量关系,再用含有字母的式子表示出来。
例:
比x的5倍多20的数。 5x+20
电器商场五一期间搞手机促销活动,上午卖出75部,下午卖出100部,已知每部手机a元,这一天一共卖出( 175a )元,上午比下午少卖出( 25a )元。
知识点二
用含有字母的式子表示稍复杂的数量关系。
计算公式中的字母一般是固定的,不能用其它字母替换,如:C表示周长、S表示面积。
公式 用字母表示
正方形的周长=边长×4 C=4a
正方形的面积=边长×边长 S=a
长方形的周长=(长+宽)×2 C=2(a+b)
长方形的面积=长×宽 S=ab
平行四边形的面积=底×高 S=ah
三角形的面积=底×高÷2 S=ah÷2
梯形的面积=(上底+下底)×高÷2 S=(a+b)h÷2
a 与2a的区别
a =a×a 表示两个a相乘
2a=2×a 表示两个a相加
当a=2或a=0时, a =2a
其余情况不相等
代入公式法:
1.周长和面积公式是固定的公式,可直接代入。
2.代入数值计算结果后,不带单位。
3.写上答语。
知识点二
用含有字母的式子表示稍复杂的数量关系。
代入法格式:
1、写当x=250时
2、代入到前面化简得式子里,必须时最简式子。
【重点:不带单位】
3.写答语。
知识点二
用含有字母的式子表示稍复杂的数量关系。
知识点三
化简含有字母的式子。
几个含有相同字母的乘法式子相加、减,可以用乘法分配律进行化简。
例:ax±bx=(a±b)x
一个运算定律中相同的量要用同一个字母表示,两个含相同字母的数进行加减,将字母前的数值进行加减,再乘字母。
例:3a+4a=7a
知识点:
一、正、负数的含义和读、写方法
二、用正负数表示生活中具有相反意义的量
一、负数的初步认识
知识点一
正、负数的含义和读、写方法
1.认识测量温度的单位,认识温度计,认识测量温度的单位(摄氏度℃、华氏度℉)
2.正、负数的读写方法
①写正数时,“+”正号可以写上,也可以省略。
读的时候带“+”正号的要读出来,不带“+”正号的省略不读。
②写负数时,“-”负号不能省略,读的时候也要读出来。
注:0既不是正数,也不是负数。它是正数和负数的分界点。
知识点二
用正负数表示生活中具有相反意义的量
①表示盈亏情况 盈利——亏损
②表示向相反方向行走的路程 向东——向西 向南——向北
……
③借助直线上的点体会正、负数的大小。
(1)“0”表示学校所在的位置,“2”表示邮局所在的位置,“-2”表示公园所在的位置。
(2) 在0的右边,向右等距离地标有1、2......各点,在0的左边,向左等距离地标有 -1、- 2......各点。
(3) 对应的正、负数到0的距离相等。如 - 2到0是2个等距离长度,2到0也是2个等距离长度。
知识点二
用正负数表示生活中具有相反意义的量
知识点:
一、平行四边形面积的计算
二、三角形面积的计算
三、梯形面积的计算
四、公顷和平方千米
五、组合图形和不规则图形的面积
二、多边形的面积
知识点一
平行四边形面积的计算
求平行四边形的面积时,底和高要对应。
平行四边形的面积=底×高 S=ah
平行四边形的底=面积÷高 a=S÷h
平行四边形的高=面积÷底 h=S÷a
知识点二
三角形面积的计算
三角形的面积=底×高÷2 S=ah÷2
三角形的底=面积×2÷高 a=2S÷h
三角形的高=面积×2÷底 h=2S÷a
等底等高的三角形面积相等
等底等高的平行四边形和三角形,三角形的面积是平行四边形面积的一半,平行四边形的面积是三角形面积的2倍。
两个完全一样的三角形可以拼成一个平行四边形。
知识点三
梯形面积的计算
梯形的面积=(上底+下底)×高÷2
S=(+b)×h÷2
两个完全相同的梯形可以拼成一个平行四边形
等高等面积的三角形和梯形,三角形的底等于梯形的上、下底之和。
1、边长是100米的正方形面积是1公顷。即1公顷=10000平方米
2、边长是1000米的正方形面积是1平方千米。平方千米有时也称平方公里。
即1平方千米=100公顷=1000000平方千米
知识点四
公顷和平方千米
知识点五
组合图形和不规则图形的面积
组合图形是由几个简单的图形组合而成的,其面积及可以看作几个简单图形的面积和,也可以看作几个简单图形的面积差。
计算组合图形的方法:
分割求和 添补求差
注:在对组合图形进行分割时,一定要考虑到分别求面积时所需要的数据条件是否充分。
计算不规则图形
1.数方格法 整格数+半格数÷2
知识点:
一、小数的意义和读、写方法
二、小数的性质和大小比较
三、大数目的改写
四、小数的近似数
三、小数的意义和性质
知识点一
小数的意义和读、写方法
1.小数的意义
分母是10.100.1000……的分数都可以用小数表示。
一位小数表示十分之几,;两位小数表示百分之几,三位小数表示千分之几...
2.小数的写法
写小数时,小数点写在个位的右下角,小数部分顺次写出每个数位上的数字。
eg: 0.01 0.04
3.小数的读法: 整数部分按整数的读法来读,小数点读作“点”,小数部分顺次读出每个数位上的数字。
eg: 0.01读作零点零一 0.04读作零点零四
知识点一
小数的意义和读、写方法
计数单位
小数点右边第一位是十分位,计数单位是 (0.1)
小数点右边第二位是百分位,计数单位是(0.01)
小数点右边第三位是千分位,计数单位是 (0.001)
小数中每相邻两个计数单位的进率都是10。
知识点二
小数的性质和大小比较
小数的性质
在小数的末尾添上“0”或去掉“0”,小数的大小不变。
根据小数的性质,通常可以去掉小数末尾的0,把小数化简。(
小数中间的0不能去)
小数的大小比较
知识点三
大数目的改写
把较大的数改写成用万做单位的小数分两步:一点二添
1点:先在这个数万位右下角点上小数点
2添:再在数的末尾填写万字
注:先分级
如果小数的未尾有0,那么不要忘了化简。
eg: 把384400改写成用万做单位的数
解析: 38.44万
如果已知数不够一万,那么整数部分要用0来占位。
如: 3350=0.335万
知识点三
大数目的改写
把较大的数改写成用万或亿做单位的小数分两步:一点二添
1点:先在这个数万位或者亿位右下角点上小数点
2添:再在数的末尾填写万字或亿字
注:先分级,四位数一级,再点小数点。
如果小数的未尾有0,那么不要忘了化简。
eg: 把384400改写成用万做单位的数 解析: 38.44万
如果已知数不够一万,那么整数部分要用0来占位。 如: 3350=0.335万
eg:把149600000改写成用亿做单位的数 解析: 1.496亿。
如果末尾有0 ,要记得化简。
知识点四
小数的近似数
求一个数的近似数的方法与求整数的近似数的方法相似,
根据要求用“四舍五入”法保留一定的小数位数。
eg: 地球和太阳之间的平均距离大约是1.496亿千米,
你知道:(1)精确到十分位大约是多少亿千米
(2) 精确到百分位大约是多少亿千米
解析:精确到十分位: 1.496亿千米≈1.5亿千米
精确到百分位: 1.496亿千米≈1.50亿千米
注:
把一个数精确到某一位,就是求这个数保留一定小数后的近似数。
知识点:
一、笔算小数加法和减法
二、用计算器计算小数加法和减法
四、小数的加法和减法
知识点一
笔算小数加法和减法
计算方法:
先把各数的小数点对齐
再按照整数加、减法的计算方法进行计算
得数里的小数点要与横线上的小数点对齐
计算结果能化简的要化简
知识点一
用计算器计算小数加法和减法
1)要按照从左到右的顺序依次按出每一个数字和运算符号:
2)如果一个小数整数部分是“0”,那么这个0可以省略不按,直接按小数点键,再依次按出小数部分的每一个数字的数字键;
(3如果一个小数的小数部分未尾有0,这个0也可以省略不按。
知识点:
一、小数乘整数
二、除数是整数的小数除法
三、小数乘小数、积的近似值
四、一个数除以小数
五、商的近似值
六、小数四则混合运算
五、小数的乘法和除法
知识点一
小数乘整数
1.小数乘整数的计算方法
①按照整数乘法计算
②因数中一共有几位小数,就从积的右边起数出几位,点上小数点
③如果积的小数位数不够,要在前面用0补位,再点上小数点;
④积的小数部分末尾的0要去掉
用竖式计算时,如果积的末尾有0
一定要先点积中的小数点
再去掉小数部分末尾的0。
知识点一
小数乘整数 小数点向右移动的变化规律
5.04×10=50.4
5.04×100=504
5.04×1000=5040
一个小数乘10、100、1000……只要把这个数的小数点向右移动一位、两位、三位……
积的变化规律
两个数相乘,
一个因数扩大(或缩小)m倍,另一个因数不变,那么它们的积也扩大 (或缩小) m倍(m≠0)。
一个因数扩大m倍,一个因数扩大n倍,积就扩大m×n倍。
两个数相乘,一个因数扩大了n倍,另一个因数缩小到原来的,那么它们的积不变。
知识点二
除数是整数的小数除法
1.小数除以整数的计算方法:
①按照整数除法的计算方法计算,商的小数点要和被除数的小数点对齐。
②如果除到被除数的未位仍有余数,要在余数后面添0继续除。
③如果小数的整数部分不够除,在商的个位上商0占位,对齐被除数的小数点,点上商的小数点,再继续除。
注:除到哪一位不够除时,
要在商的那一位上商0占位,
然后继续除。
知识点二
除数是整数的小数除法
小数点向左移动的变化规律
21.5÷10=2.15
21.5÷100=0.215
21.5÷1000=0.0215
小数点向左移动引起小数大小的变化规律:
一个数除以10、100、1000……只要把这个小数点向左移动一位、两位、三位······
差倍问题
已知两个数的差及它们的倍数关系,求这两个数的问题就是差倍问题
在差倍问题中,
小数=差÷ (倍数一1)
大数=差+小数或大数=小数X倍数
例:一个小数,如果把小数点向右移动一位,所得的数比原来增加63.72,这个小数是多少
解析:
把一个小数的小数点向右移动一位,所得的数就扩大到原来的10倍,即所得的数比原来增加了10-1 = 9倍,已知所得的数比原来增加了63.72,说明原数的(10-1) 倍正好是63.72,求原数是多少,用除法计算。
10-1=9 63.72÷9=7.08
商的变化规律
商的变化规律:
被除数不变,除数扩大(或缩小)多少倍,商就缩小或(扩大)多少倍
除数不变,被除数扩大(或缩小)多少倍,商就扩大(或缩小)多少倍
被除数和除数同时乘或除以一个相同的数(0除外),商不变
知识点三
小数乘小数
①按照整数乘法的计算方法算出积
②看因数中一共有几位小数,就从积的右边起数出几位,点上小数点
③积的小数位数如果不够,要先在前面用 0 补位,再点上小数点
④积的小数部分未尾有0,要根据小数的性质去掉。
知识点三
小数乘小数 积的大小与因数的关系
①一个数(0除外) 乘大于1的数,积大于原来的数;
②一个数(0除外) 乘小于1的数,积小于原来的数;
③一个数 (0除外) 乘1,积等于原来的数。
知识点三
小数乘小数 积的近似值
求积的近似值,要先算出积,再看需要保留位数的后一位上的数字,最后按照“四舍五入”法求出结果,并用“≈”连接。
知识点四
一个数除以小数
一个数除以小数的计算方法:
①先移动除数的小数点,使它变成整数
②除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数的未尾用0补足)
③然后按除数是整数的小数除法进行计算
注:除数是小数的除法,商的小数点应与被除数移动后的小数点对齐,与移动前的小数点无关。
知识点四
一个数除以小数 商与被除数的大小关系
①一个数(0除外) 除以大于1的数,商小于原来的数;
②一个数(0除外) 除以小于1的数,商大于原来的数;
③一个数 (0除外) 除以1,商等于原来的数。
知识点五
商的近似值 四舍五入法
用四舍五入法求商的近似值
求商的近似值,一般先算出比需要保留的小数位数多一位的商,
再按照“四舍五人”法写出结果。
5.713÷3≈1.90(保留两位小数)
注求商的近似数时,有时保留指定小数位数后,近似数的末尾有0,此时0不能去掉。
知识点五 循环小数
注:循环小数一定是无限小数,无限小数不一定是循环小数
知识点五
商的近似值 用“进一法”或“去尾法”解决问题
在解决实际问题时,取商的近似值可以根据具体的情况采用进一法或去尾法。
注:现实生活中,求最多能做多少套衣服、最多能买多少本书等问题,应采用去尾法。
注现实生活中,求至少需要几辆车才能运完,至少需要几个箱子才能装下等问题,应采用进一法。
知识点六 小数四则混合运算
1.小数的四则混合运算:
(1)小数四则混合运算和整数四则混合运算的运算顺序相同:
在没有括号的算式里,如果只有加减法或乘除法,要从左到右依次计算;
如果既有加减法,又有乘除法,要先算乘除法,后算加减法。
有括号,要先算括号里面的,再算括号外面的。
知识点六 小数四则混合运算
整数运算定律在小数中的应用
①整数加法的运算定律、减法的运算性质对小数加减法同样适用
②整数乘法的交换律、结合律和分配律、除法的运算性质对小数乘除法同样适用
(3)应用运算定律可以使一些计算简便。
知识点:
一、复式统计表
二、复式条形统计图(二)
六、统计表和条形统计图(二)
知识点一 复式统计表
1、复式统计表能把两个 (或多个) 统计内容 (单式统计表)的数据合并在一张表上。
2、特点: 第一栏左上角一般为表头意横栏中各个数据的和用合计表示 ,竖栏中各个数据的和用总计表示。
注:
复式统计表的优点: 不仅能反映每个类别的数据情况,更能从整体上反映所有类别的数据情况。
知识点一 复式统计表
填写复式统计表的方法与填写单式统计表的方法基本相同.
需要计算出合计数和总计数
①填写表头:确定横栏与竖栏表示的内容
②填入每组别对应的数据,并计算“合计数”“总计”;
③填写标题和制表日期。
知识点二 复式条形统计图(二)
1、定义:在同一幅条形统计图中,用两种 (或多种) 不同的直条描述两组 (或多组)不同的数据,这样的统计图叫做复式条形统计图。
2、特点: 不但可以清楚地表示出各种数量的多少,而且能直观、形象地比较两种或多种数量之间的关系。
①写出标题和制图日期
②确定横轴和纵轴:注明所代表的事物
③横轴:直条的宽度和间隔纵轴:确定单位长度
④根据数据画出相应的直条
⑤标明图例,涂上不同的颜色 (或底纹)
注:在绘制复式条形统计图时,一定要画出图例,条形的宽度要一致,间隔要相等,单位长度要统一。
知识点:
用列举的策略解决问题
七、解决问题的策略
用列举的策略解决问题
用列举的策略解决问题时:
要先按一定的顺序将所有的情况列举出来
再从中找出符合要求的答案
eg: 4个朋友见面,每两人握手,一共要握___6___次手。
注:列举时不能杂乱无章地罗列,要按一定的顺序,这样才能做到不重复.不遗漏。
知识点:
一、用含有字母的式子表示简单的数量关系。
二、用含有字母的式子表示稍复杂的数量关系和公式。
三、化简含有字母的式子。
八、用字母表示数
知识点一
用含有字母的式子表示简单的数量关系。
1.用字母可以表示数,用含有字母的式子可以表示数量关系。
2.当字母的值确定时,含有字母的式子的值也随之确定。
注:
①在含有字母的式子里,字母的值要符合实际情况
②当数与字母相乘时,中间的乘号可以省略不写,省略乘号时,一般把数写在字母的前面(只有×可以省略)
例:x×8a=8x
③如果字母与1相乘,可以省略1与乘号。
例:1×n=n
知识点二
用含有字母的式子表示稍复杂的数量关系。
根据题意,找出题目中的数量关系,再用含有字母的式子表示出来。
例:
比x的5倍多20的数。 5x+20
电器商场五一期间搞手机促销活动,上午卖出75部,下午卖出100部,已知每部手机a元,这一天一共卖出( 175a )元,上午比下午少卖出( 25a )元。
知识点二
用含有字母的式子表示稍复杂的数量关系。
计算公式中的字母一般是固定的,不能用其它字母替换,如:C表示周长、S表示面积。
公式 用字母表示
正方形的周长=边长×4 C=4a
正方形的面积=边长×边长 S=a
长方形的周长=(长+宽)×2 C=2(a+b)
长方形的面积=长×宽 S=ab
平行四边形的面积=底×高 S=ah
三角形的面积=底×高÷2 S=ah÷2
梯形的面积=(上底+下底)×高÷2 S=(a+b)h÷2
a 与2a的区别
a =a×a 表示两个a相乘
2a=2×a 表示两个a相加
当a=2或a=0时, a =2a
其余情况不相等
代入公式法:
1.周长和面积公式是固定的公式,可直接代入。
2.代入数值计算结果后,不带单位。
3.写上答语。
知识点二
用含有字母的式子表示稍复杂的数量关系。
代入法格式:
1、写当x=250时
2、代入到前面化简得式子里,必须时最简式子。
【重点:不带单位】
3.写答语。
知识点二
用含有字母的式子表示稍复杂的数量关系。
知识点三
化简含有字母的式子。
几个含有相同字母的乘法式子相加、减,可以用乘法分配律进行化简。
例:ax±bx=(a±b)x
一个运算定律中相同的量要用同一个字母表示,两个含相同字母的数进行加减,将字母前的数值进行加减,再乘字母。
例:3a+4a=7a
