【精选备课】2022-2023学年华师大版数学七年级上册 3.4.2 合并同类项 学案(无答案)
文档属性
| 名称 | 【精选备课】2022-2023学年华师大版数学七年级上册 3.4.2 合并同类项 学案(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 36.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 13:19:27 | ||
图片预览


文档简介
合并同类项
【学习目标】
1.同类项的概念及合并同类项的方法。
2.准确理解同类项概念的含义。
【学习重难点】
1.重点:同类项的概念 及合并同类项的方法。
2.难点:准确理解同类项概念的含义。
【学习过程】
一、自主探究。
1.思考问题:什么是同类项?
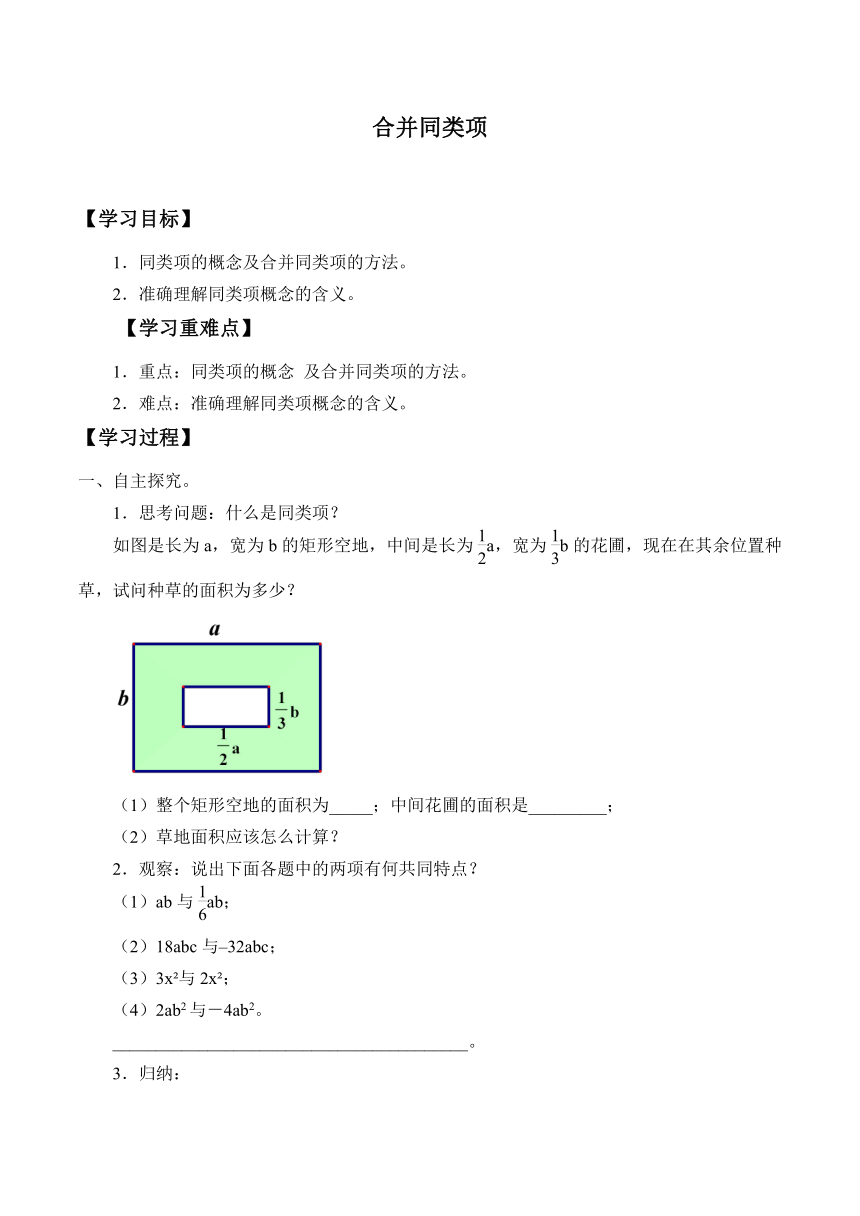
如图是长为a,宽为b的矩形空地,中间是长为a,宽为b的花圃,现在在其余位置种草,试问种草的面积为多少?
(1)整个矩形空地的面积为_____;中间花圃的面积是_________;
(2)草地面积应该怎么计算?
2.观察:说出下面各题中的两项有何共同特点?
(1)ab与ab;
(2)18abc与–32abc;
(3)3x 与2x ;
(4)2ab2与-4ab2。
_________________________________________。
3.归纳:
(1)我们把所含字母____,并且_________也相同的项叫做同类项。(注意:几个常数项也是同类项)
(2)同类项的两个相同:
①所含字母相同;
②相同字母的次数相同。
(3)同类项的两个无关:
①与系数大小无关;
②与字母顺序无关。
二、跟踪训练一。
1.请你来判断:下列各题中的两式是同类项的打√,不是的打×。
(1)a2 与3a2( );
(2)a2b与 a2c ( );
(3)m n与3mn2( );
(4)5x y与-yx ( );
(5)与–2 ( );
(6)2(a+b)与-3(b+a)( )。
2.找出下面多项式中的同类项(可用不同的符号标出)。
(1)4x +2x+7+3x-8x -2
(2)4a2+3b2+2ab-4a2-4b2
反思交流:判断同类项的两个条件是什么?
三、深入探究。
1.思考问题:怎样合并同类项?
(1)运用有理数的运算律计算:
89×3+11×3=( )×3
89×(-3)+11×(-3)=( )×(-3)
你能类比上面数的运算完成下面的填空吗?试一试。
89a+11a=( )a;
3x +2x =( )x ;
2ab2-4ab2=( )ab2。
上面三个式子的结果你是怎样得到的?你能说说怎样合并同类项吗?
归纳:合并同类项时,只须将同类项的系数___,字母及其指数____。
注意:合并同类项的实质是对其_______相加减,各个字母______,各字母的指数______。
2.知识运用:
例题1:对于下列多项式,合并同类项。
(1)2x4-3x +7x–5x -4x+9+8x –3x;
(2)x y+6xy +3x y-4xy +10xy。
方法:
①先确定同类项(用相同的标记标出,对于不同的同类项,用不同的标记);
②运用加法的交换律和结合律把同类项括在一起(连同前面的符号);
③将同类项系数相加、减,字母与其指数不变。
例题2:当k取何值时,单项式3xky与-x y是同类项?
四、跟踪训练二。
1.直接写出下列各式的结果:
(1)7a2b+2a2b=____;
(2)3xy -5xy =____;
(3)-2xy+2xy=_____;
(4)2x+3x-x=____。
2.下列运算正确的是( )
A.5a2-3a2=2 B.2x +3x=5x
C.x+x+x=x D.6ab-7ab=-ab
【达标检测】
一、合并下列各式中的同类项:
1.-3x y+2x y+3xy -2xy ;
2.4a2+3b2+2ab-4a2-4b2;
3.4x +2x+7+3x-8x -5x;
4.-2x +7x –5x+4–5x +10x;
5.3x4y+2xy –x4y+5xy –y4。
二、填空:
1.任意写出-3a2b的一个同类项________。
2.如果2xnym与-3x y n是同类项,则n=____,m=___。
三、选择:
1.下列各式正确的个数有( )
①8x+5y=13xy ② 2a2+a2=3a4
③5x-3x=2 ④7x y-2x y-x y=4x y
A.1个 B.2个 C.3个 D.4个
【学习目标】
1.同类项的概念及合并同类项的方法。
2.准确理解同类项概念的含义。
【学习重难点】
1.重点:同类项的概念 及合并同类项的方法。
2.难点:准确理解同类项概念的含义。
【学习过程】
一、自主探究。
1.思考问题:什么是同类项?
如图是长为a,宽为b的矩形空地,中间是长为a,宽为b的花圃,现在在其余位置种草,试问种草的面积为多少?
(1)整个矩形空地的面积为_____;中间花圃的面积是_________;
(2)草地面积应该怎么计算?
2.观察:说出下面各题中的两项有何共同特点?
(1)ab与ab;
(2)18abc与–32abc;
(3)3x 与2x ;
(4)2ab2与-4ab2。
_________________________________________。
3.归纳:
(1)我们把所含字母____,并且_________也相同的项叫做同类项。(注意:几个常数项也是同类项)
(2)同类项的两个相同:
①所含字母相同;
②相同字母的次数相同。
(3)同类项的两个无关:
①与系数大小无关;
②与字母顺序无关。
二、跟踪训练一。
1.请你来判断:下列各题中的两式是同类项的打√,不是的打×。
(1)a2 与3a2( );
(2)a2b与 a2c ( );
(3)m n与3mn2( );
(4)5x y与-yx ( );
(5)与–2 ( );
(6)2(a+b)与-3(b+a)( )。
2.找出下面多项式中的同类项(可用不同的符号标出)。
(1)4x +2x+7+3x-8x -2
(2)4a2+3b2+2ab-4a2-4b2
反思交流:判断同类项的两个条件是什么?
三、深入探究。
1.思考问题:怎样合并同类项?
(1)运用有理数的运算律计算:
89×3+11×3=( )×3
89×(-3)+11×(-3)=( )×(-3)
你能类比上面数的运算完成下面的填空吗?试一试。
89a+11a=( )a;
3x +2x =( )x ;
2ab2-4ab2=( )ab2。
上面三个式子的结果你是怎样得到的?你能说说怎样合并同类项吗?
归纳:合并同类项时,只须将同类项的系数___,字母及其指数____。
注意:合并同类项的实质是对其_______相加减,各个字母______,各字母的指数______。
2.知识运用:
例题1:对于下列多项式,合并同类项。
(1)2x4-3x +7x–5x -4x+9+8x –3x;
(2)x y+6xy +3x y-4xy +10xy。
方法:
①先确定同类项(用相同的标记标出,对于不同的同类项,用不同的标记);
②运用加法的交换律和结合律把同类项括在一起(连同前面的符号);
③将同类项系数相加、减,字母与其指数不变。
例题2:当k取何值时,单项式3xky与-x y是同类项?
四、跟踪训练二。
1.直接写出下列各式的结果:
(1)7a2b+2a2b=____;
(2)3xy -5xy =____;
(3)-2xy+2xy=_____;
(4)2x+3x-x=____。
2.下列运算正确的是( )
A.5a2-3a2=2 B.2x +3x=5x
C.x+x+x=x D.6ab-7ab=-ab
【达标检测】
一、合并下列各式中的同类项:
1.-3x y+2x y+3xy -2xy ;
2.4a2+3b2+2ab-4a2-4b2;
3.4x +2x+7+3x-8x -5x;
4.-2x +7x –5x+4–5x +10x;
5.3x4y+2xy –x4y+5xy –y4。
二、填空:
1.任意写出-3a2b的一个同类项________。
2.如果2xnym与-3x y n是同类项,则n=____,m=___。
三、选择:
1.下列各式正确的个数有( )
①8x+5y=13xy ② 2a2+a2=3a4
③5x-3x=2 ④7x y-2x y-x y=4x y
A.1个 B.2个 C.3个 D.4个
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
