2022-2023学年七年级数学上册(苏科版)专题6.3 余角、补角、对顶角(知识解读)(含解析)
文档属性
| 名称 | 2022-2023学年七年级数学上册(苏科版)专题6.3 余角、补角、对顶角(知识解读)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 492.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 00:00:00 | ||
图片预览




文档简介
专题6.3 余角、补角、对顶角(知识解读)
【学习目标】
1.理解并掌握对顶角的概念及性质,会用对顶角的性质解决一些实际问题;
2.理解并掌握补角和余角的概念及性质,会运用其解决一些实际问题.
3.理解并掌握对顶角和邻补角定义,性质,会运用其性质进行有关的运算。
【知识点梳理】
考点1 余角
(1)定义:一般地,如果两个角的和等于90°(直角),我们就说这两个角互为余角,称其中的一个角是另一个角的余角.
(2)余角的性质:同角(等角)的余角相等.
(3)数学语言表示:若∠1+∠2=90°,则∠1与∠2互余,若∠1与∠2互余,则∠1+∠2=90°.
考点2 补角
(1)定义:一般地,如果两个角的和等于180°(平角),我们就说这两个角互为补角,称其中一个角是另一个角的补角.
(2)补角的性质:同角(等角)的补角相等.
(3)数学语言表示:若∠1+∠2=180°,则∠1与∠2互补,若∠1与∠2互补,则∠1+∠2=180°.
考点3:相交线
(1)相交线概念:两条不同的直线,如有公共点则称这两条直线相交,这个公共点称为两条直线的交点。
(1)相交线的性质:两直线相交只有一个交点。
注意:(1)两条直线相交可以形成四个角。
(2)其中不超过的角称为两直线的夹角。
(3)两直线有一个交点,则两直线相交。
两线四角:两条直线相交,会出现四个角。
考点4 对顶角
(1)概念:∠1与∠3 有公共顶点O,而没有公共边,其中∠1的两边OA、OD是∠3的两边OB、OC的反向延长线,具有这种关系的两个角叫做互为对顶角。
互为对顶角:∠1=∠3, ∠2=∠4.
(2)对顶角的性质:对顶角相等
考点5 邻补角的
(1)概念:如图:∠1与∠2有一条公共边OD,它们的另外一条边为OA、OB互为反向延长线,具有这种关系的两个角叫做互为邻补角。
互为邻补角:∠1与∠2,∠2与∠3, ∠3与∠4,∠1与∠4。
(2)性质:邻补角相加180°
【典例分析】
【考点1 余角和补角及有关运算】
【典例1-1】(2022秋 思明区校级月考)已知∠α=25°30',则它的补角为( )
A.25°30′ B.64° 30' C.164° 30' D.154°30′
【典例1-2】(2022秋 泰山区校级月考)如图,已知∠BAC=90°,AD⊥BC,垂足是D,则图中与∠B互余的角有( )
A.1个 B.2个 C.3个 D.4个
【变式1-1】(2022春 舞钢市期中)若∠A=50°,则∠A的余角的度数是( )
A.40° B.130° C.90° D.180°
【变式1-1】(2021秋 重庆期末)已知∠α=35°40′,则∠α的补角的度数为( )
A.55°60′ B.55°20′ C.144°60′ D.144°20′
【变式1-3】(2022 新华区校级一模)在下列各图中,∠1与∠2一定是互补关系的是( )
A. B.
C. D.
【典例2】(2021秋 秀屿区校级期末)已知一个角的余角比它的补角的还少5°,求这个角.
【变式2-1】(2021秋 梁平区期末)若一个角的补角加上20°后等于这个角余角的3倍,则这个角的度数为( )
A.25° B.35° C.45° D.55°
【变式2-2】(2021秋 启东市期末)若一个角的余角是它的补角的,则这个角的度数是( )
A.30° B.60° C.120° D.150°
【变式2-3】(2022春 聊城期末)一个角的补角加上30°后,等于这个角的余角的4倍,则这个角的度数为( )
A.60° B.50° C.45° D.40°
【典例3】(2021秋 栾城区期末)如图,点A、O、B在同一条直线上.
(1)∠AOC比∠BOC大100°,求∠AOC与∠BOC的度数;
(2)在(1)的条件下,若∠BOC与∠BOD互余,求∠BOD的度数;
(3)在(1)(2)的条件下,若OE平分∠AOC,求∠DOE的度数.
【变式3】(2021秋 西宁期末)如图,点A,O,B在一条直线上,∠AOC=3∠COD,OE平分∠BOD.
(1)若∠COD=10°,求∠AOC的余角的度数;
(2)若∠AOC=45°,求∠COE的度数.
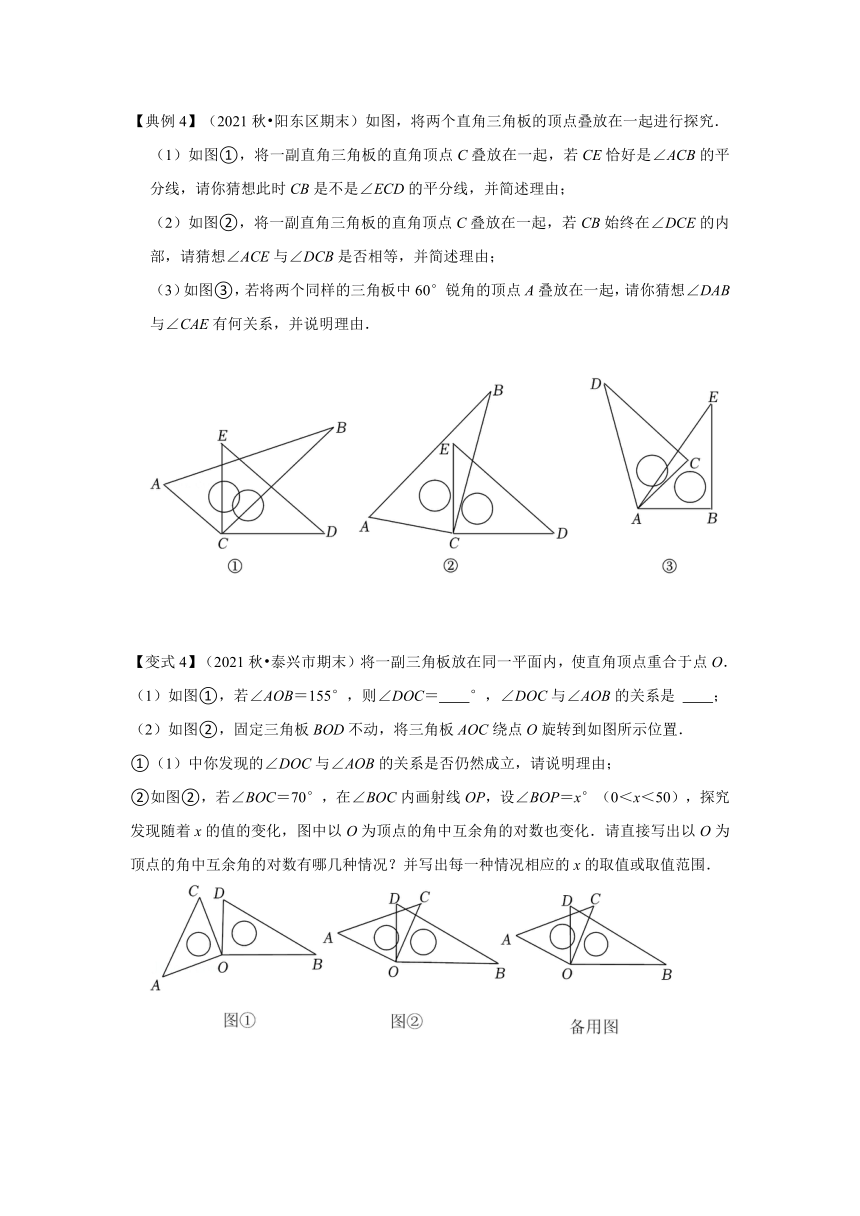
【典例4】(2021秋 阳东区期末)如图,将两个直角三角板的顶点叠放在一起进行探究.
(1)如图①,将一副直角三角板的直角顶点C叠放在一起,若CE恰好是∠ACB的平分线,请你猜想此时CB是不是∠ECD的平分线,并简述理由;
(2)如图②,将一副直角三角板的直角顶点C叠放在一起,若CB始终在∠DCE的内部,请猜想∠ACE与∠DCB是否相等,并简述理由;
(3)如图③,若将两个同样的三角板中60°锐角的顶点A叠放在一起,请你猜想∠DAB与∠CAE有何关系,并说明理由.
【变式4】(2021秋 泰兴市期末)将一副三角板放在同一平面内,使直角顶点重合于点O.
(1)如图①,若∠AOB=155°,则∠DOC= °,∠DOC与∠AOB的关系是 ;
(2)如图②,固定三角板BOD不动,将三角板AOC绕点O旋转到如图所示位置.
①(1)中你发现的∠DOC与∠AOB的关系是否仍然成立,请说明理由;
②如图②,若∠BOC=70°,在∠BOC内画射线OP,设∠BOP=x°(0<x<50),探究发现随着x的值的变化,图中以O为顶点的角中互余角的对数也变化.请直接写出以O为顶点的角中互余角的对数有哪几种情况?并写出每一种情况相应的x的取值或取值范围.
【考点2 相交线】
【典例5】(2022春 龙岗区校级期中)观察如图图形,并阅读相关文字:那么5条直线相交,最多交点的个数是( )
A.10 B.14 C.21 D.15
【变式5-1】(2021秋 让胡路区校级期末)如果同一平面内有三条直线,那么它们交点个数是( )个.
A.3个 B.1或3个
C.1或2或3个 D.0或1或2或3个
【变式5-2】(2022春 昭阳区校级月考)已知2条直线最多有=1个交点,3条直线最多有=3个交点,4条直线最多有=6个交点,…由此猜想,8条直线最多有个交点( )
A.16 B.28 C.32 D.40
【考点3 对顶角和邻补角及有关运算】
【典例6】(2022秋 南岗区校级月考)如图中,∠1和∠2是对顶角的是( )
A. B.
C. D.
【变式6】(2022春 江津区校级期中)下列各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
【典例7】(2022春 重庆月考)下面四个图形中,∠1与∠2是邻补角的是( )
A. B.
C. D.
【变式7】(2022春 横县期中)下列各图中,∠1与∠2是邻补角的是( )
A. B.
C. D.
【典例8】(2022春 仓山区校级期末)如图,直线AC,BD相交于点O,∠AOB=48°,则∠COD的度数是( )
A.42° B.48° C.96° D.132°
【变式8-1】(2022春 来凤县期末)如图,已知直线AB与CD相交于点O,OA平分∠COE,若∠DOE=70°,则∠BOD度数是( )
A.75° B.65° C.55° D.105°
【变式8-2】(2022春 东莞市期中)若∠A=54°,则∠A的邻补角是( )
A.36° B.126° C.46° D.136°
【典例9】(2022春 和平区校级月考)如图,直线EF,CD相交于点O,OC平分∠AOF,∠AOE=2∠BOD.
(1)若∠AOE=40°,求∠DOE的度数;
(2)猜想OA与OB之间的位置关系,并证明.
【变式9-1】(2022春 碑林区校级月考)如图,直线AB与CD相交于点O,∠COE=80°,∠COF:∠AOC=2:3,射线OE平分∠BOF,求∠BOD的度数.
【变式9-2】(2022春 鼓楼区期中)如图,直线AB和直线CD相交于点O,OB平分∠EOD.
(1)写出图中∠BOD的对顶角 ,和两个邻补角 ;
(2)若∠BOD=40°,求∠EOC的度数.
【变式9-3】(2022春 东莞市期中)如图,直线AB,CD相交于O,OE是∠COB的角平分线.
(1)∠AOC的对顶角是 ;
(2)若∠BOC=130°,求∠BOD、∠DOE的度数.
专题6.3 余角、补角、对顶角(知识解读)
【学习目标】
1.理解并掌握对顶角的概念及性质,会用对顶角的性质解决一些实际问题;
2.理解并掌握补角和余角的概念及性质,会运用其解决一些实际问题.
3.理解并掌握对顶角和邻补角定义,性质,会运用其性质进行有关的运算。
【知识点梳理】
考点1 余角
(1)定义:一般地,如果两个角的和等于90°(直角),我们就说这两个角互为余角,称其中的一个角是另一个角的余角.
(2)余角的性质:同角(等角)的余角相等.
(3)数学语言表示:若∠1+∠2=90°,则∠1与∠2互余,若∠1与∠2互余,则∠1+∠2=90°.
考点2 补角
(1)定义:一般地,如果两个角的和等于180°(平角),我们就说这两个角互为补角,称其中一个角是另一个角的补角.
(2)补角的性质:同角(等角)的补角相等.
(3)数学语言表示:若∠1+∠2=180°,则∠1与∠2互补,若∠1与∠2互补,则∠1+∠2=180°.
考点3:相交线
(1)相交线概念:两条不同的直线,如有公共点则称这两条直线相交,这个公共点称为两条直线的交点。
(1)相交线的性质:两直线相交只有一个交点。
注意:(1)两条直线相交可以形成四个角。
(2)其中不超过的角称为两直线的夹角。
(3)两直线有一个交点,则两直线相交。
两线四角:两条直线相交,会出现四个角。
考点4 对顶角
(1)概念:∠1与∠3 有公共顶点O,而没有公共边,其中∠1的两边OA、OD是∠3的两边OB、OC的反向延长线,具有这种关系的两个角叫做互为对顶角。
互为对顶角:∠1=∠3, ∠2=∠4.
(2)对顶角的性质:对顶角相等
考点5 邻补角的
(1)概念:如图:∠1与∠2有一条公共边OD,它们的另外一条边为OA、OB互为反向延长线,具有这种关系的两个角叫做互为邻补角。
互为邻补角:∠1与∠2,∠2与∠3, ∠3与∠4,∠1与∠4。
(2)性质:邻补角相加180°
【典例分析】
【考点1 余角和补角及有关运算】
【典例1-1】(2022秋 思明区校级月考)已知∠α=25°30',则它的补角为( )
A.25°30′ B.64° 30' C.164° 30' D.154°30′
【答案】D
【解答】解:180°﹣25°30′=154°30′.
故选:D.
【典例1-2】(2022秋 泰山区校级月考)如图,已知∠BAC=90°,AD⊥BC,垂足是D,则图中与∠B互余的角有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【解答】解:∵∠BAC=90°,
∴∠ABD+∠C=90°;
又∵AD⊥BC,
∴∠BDA=90°,
∴∠B+∠BAD=90°,
故图中与∠B互余的角有2个.
故选:B.
【变式1-1】(2022春 舞钢市期中)若∠A=50°,则∠A的余角的度数是( )
A.40° B.130° C.90° D.180°
【答案】A
【解答】解:∠A的余角=90°﹣50°=40°.
故答案为:A.
【变式1-1】(2021秋 重庆期末)已知∠α=35°40′,则∠α的补角的度数为( )
A.55°60′ B.55°20′ C.144°60′ D.144°20′
【答案】D
【解答】解:∵∠α=35°40′,
∴∠α的补角的度数为180°﹣35°40′=144°20′.
故选:D.
【变式1-3】(2022 新华区校级一模)在下列各图中,∠1与∠2一定是互补关系的是( )
A. B.
C. D.
【答案】B
【解答】解:对于A选项,∠1与∠2为对顶角,
∴∠1=∠2,不一定是互补关系,
故A选项错误;
对于B选项,由平角的定义可得∠1+∠2=180°,
∴∠1与∠2是互补关系,
故B选项正确;
对于C选项,根据三角形内角和定理可知,
∠1+∠2=90°,
∴∠1与∠2是互余关系,
故C选项错误;
对于D选项,∠1与∠2为同旁内角,
当两直线平行时,∠1与∠2互补,否则不一定互补,
故D选项错误.
故选:B.
【典例2】(2021秋 秀屿区校级期末)已知一个角的余角比它的补角的还少5°,求这个角.
【解答】解:设这个角的度数是x°,
则90﹣x=(180﹣x)﹣5,
解得:x=27,
即这个角的度数是27°,
答:这个角的度数是27°.
【变式2-1】(2021秋 梁平区期末)若一个角的补角加上20°后等于这个角余角的3倍,则这个角的度数为( )
A.25° B.35° C.45° D.55°
【答案】B
【解答】解:设这个角为x,则它的余角为90°﹣x,补角180°﹣x,
根据题意得,180°﹣x+20°=3(90°﹣x),
解得x=35°.
故选:B.
【变式2-2】(2021秋 启东市期末)若一个角的余角是它的补角的,则这个角的度数是( )
A.30° B.60° C.120° D.150°
【答案】A
【解答】解:设这个角为α,则它的余角为90°﹣α,它的补角为180°﹣α.
由题意得,90°﹣α=(180°﹣α),
解得:α=30°.
故这个角的度数为30°.
故选:A.
【变式2-3】(2022春 聊城期末)一个角的补角加上30°后,等于这个角的余角的4倍,则这个角的度数为( )
A.60° B.50° C.45° D.40°
【答案】B
【解答】解:设这个角的度数为x.
由题意得,180°﹣x+30°=4(90°﹣x).
∴x=50°.
故选:B
【典例3】(2021秋 栾城区期末)如图,点A、O、B在同一条直线上.
(1)∠AOC比∠BOC大100°,求∠AOC与∠BOC的度数;
(2)在(1)的条件下,若∠BOC与∠BOD互余,求∠BOD的度数;
(3)在(1)(2)的条件下,若OE平分∠AOC,求∠DOE的度数.
【解答】解:(1)∵∠AOC比∠BOC大100°,
∴∠AOC=∠BOC+100°,
又点A、O、B在同一条直线上.
∴∠AOC+∠BOC=180°,
∴∠BOC+100°+∠BOC=180°,
∴∠BOC=40°,
∠AOC=140°;
(2)∵∠BOC与∠BOD互余,
∴∠BOD+∠BOC=90°,
∴∠BOD=90°﹣∠BOC=90°﹣40°=50°;
(3)∵OE平分∠AOC,
∴得∠COE=∠AOC=70°,
∵∠BOD+∠BOC=90°,
∴∠DOE=∠COE+∠COD=∠COE+∠BOD+∠BOC
=70°+90°
=160°.
【变式3】(2021秋 西宁期末)如图,点A,O,B在一条直线上,∠AOC=3∠COD,OE平分∠BOD.
(1)若∠COD=10°,求∠AOC的余角的度数;
(2)若∠AOC=45°,求∠COE的度数.
【解答】解:(1)∵∠AOC=3∠COD,∠COD=10°,
∴∠AOC=30°,
∴∠AOC的余角=90°﹣30°=60°,
∴∠AOC的余角的度数是60°;
(2)∵∠AOC=3∠COD,∠AOC=45°,
∴,
∵点A,O,B在一条直线上,
∴∠AOB=180°,
∴∠BOD=180°﹣∠AOC﹣∠COD=180°﹣45°﹣15°=120°,
∵OE平分∠BOD,
∴,
∴∠COE=∠COD+∠DOE=15°+60°=75°,
∴∠COE的度数为75°.
【典例4】(2021秋 阳东区期末)如图,将两个直角三角板的顶点叠放在一起进行探究.
(1)如图①,将一副直角三角板的直角顶点C叠放在一起,若CE恰好是∠ACB的平分线,请你猜想此时CB是不是∠ECD的平分线,并简述理由;
(2)如图②,将一副直角三角板的直角顶点C叠放在一起,若CB始终在∠DCE的内部,请猜想∠ACE与∠DCB是否相等,并简述理由;
(3)如图③,若将两个同样的三角板中60°锐角的顶点A叠放在一起,请你猜想∠DAB与∠CAE有何关系,并说明理由.
【解答】解:(1)CB是∠ECD的平分线,
理由:∵∠ACB=90°,CE是∠ACB的平分线,
∴∠ECB=∠ACB=45°,
∴∠DCB=∠ECD﹣∠ECB=90°﹣45°=45°,
∴∠ECB=∠DCB,
∴CB是∠ECD的平分线;
(2)∠ACE=∠DCB,
理由:∵∠ACB=∠DCE=90°,
∴∠ACE+∠ECB=90°,∠DCB+∠ECB=90°,
∴∠ACE=∠DCB;
(3)∠DAB+∠EAC=120°,
理由:∵∠DAC=∠EAB=60°,
∴∠DAE+∠EAC=60°,∠EAC+∠CAB=60°,
∴∠DAE+∠EAC+∠EAC+∠CAB=120°,
∵∠DAE+∠EAC+∠CAB=∠DAB,
∴∠DAB+∠CAE=120°.
【变式4】(2021秋 泰兴市期末)将一副三角板放在同一平面内,使直角顶点重合于点O.
(1)如图①,若∠AOB=155°,则∠DOC= °,∠DOC与∠AOB的关系是 ;
(2)如图②,固定三角板BOD不动,将三角板AOC绕点O旋转到如图所示位置.
①(1)中你发现的∠DOC与∠AOB的关系是否仍然成立,请说明理由;
②如图②,若∠BOC=70°,在∠BOC内画射线OP,设∠BOP=x°(0<x<50),探究发现随着x的值的变化,图中以O为顶点的角中互余角的对数也变化.请直接写出以O为顶点的角中互余角的对数有哪几种情况?并写出每一种情况相应的x的取值或取值范围.
【解答】解:(1)由题意可知,∠AOC=∠BOD=90°,
∵∠AOB=155°,
∴∠COD=360°﹣∠AOC﹣∠BOD﹣∠AOB=25°,
∴∠AOB+∠COD=155°+25°=180°;
故答案为:25;互补;
(2)①成立;
理由:∠DOC+∠AOB
=∠AOC﹣∠AOD+∠DOB+∠AOD
=∠AOC+∠DOB
=90°+90°
=180°;
②∵∠BOC=70°,
∴∠COD=20°,
∴∠AOD=70°;此时有两对角互余,∠AOD和∠COD,∠BOC和∠COD;
当共有3种情况:
当x=35时,∠BOP=∠COP=35°,则∠BOP+∠DOP=∠COP+∠DOP=90°,
此时互余的角有4对:∠AOD和∠COD,∠BOC和∠COD,∠BOP和∠DOP,∠COP和∠DOP;
当x=20时,∠BOC=∠AOD=∠DOP=70°,∠COD=∠COP=20°,
此时,互余的角有6对:∠AOD和∠COD,∠BOC和∠COD,∠DOP和∠COD,∠AOD和∠BOP,∠BOC和∠BOP,∠DOP和∠BOP;
当0<x<50且x≠35和20时,
此时互余的角有3对:∠AOD和∠COD,∠BOC和∠COD,∠BOP和∠DOP.
【考点2 相交线】
【典例5】(2022春 龙岗区校级期中)观察如图图形,并阅读相关文字:那么5条直线相交,最多交点的个数是( )
A.10 B.14 C.21 D.15
【答案】A
【解答】解:两条直线相交,最多交点数为1个;
三条直线相交,最多交点数为1+2=3(个);
四条直线相交,最多交点数为1+2+3=6(个);
五条直线相交,最多交点数为1+2+3+4=10(个).
故选:A.
【变式5-1】(2021秋 让胡路区校级期末)如果同一平面内有三条直线,那么它们交点个数是( )个.
A.3个 B.1或3个
C.1或2或3个 D.0或1或2或3个
【答案】D
【解答】解:当三条直线平行时,交点个数为0;
当三条直线相交于1点时,交点个数为1;
当三条直线中,有两条平行,另一条分别与他们相交时,交点个数为2;
当三条直线互相不平行时,交点个数为3;
所以,它们的交点个数有4种情形.
故选:D.
【变式5-2】(2022春 昭阳区校级月考)已知2条直线最多有=1个交点,3条直线最多有=3个交点,4条直线最多有=6个交点,…由此猜想,8条直线最多有个交点( )
A.16 B.28 C.32 D.40
【答案】B
【解答】解:∵2条直线最多有=1个交点,
3条直线最多有=3个交点,
4条直线最多有=6个交点,
……
n条直线最多有个交点,
∴n=8时,==28.
故选:B
【考点3 对顶角和邻补角及有关运算】
【典例6】(2022秋 南岗区校级月考)如图中,∠1和∠2是对顶角的是( )
A. B.
C. D.
【答案】B
【解答】解:由对顶角的定义可知,
图中的∠1与∠2是对顶角,
故选:B.
【变式6】(2022春 江津区校级期中)下列各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
【答案】C
【解答】解:根据对顶角的定义可知:只有C选项中的是对顶角,其它都不是.
故选:C.
【典例7】(2022春 重庆月考)下面四个图形中,∠1与∠2是邻补角的是( )
A. B.
C. D.
【答案】C
【解答】解:根据邻补角的定义可知,
图中的∠1与∠2是邻补角,
故选:C.
【变式7】(2022春 横县期中)下列各图中,∠1与∠2是邻补角的是( )
A. B.
C. D.
【答案】C
【解答】解:A.根据邻补角的定义,A中∠1与∠2不是邻补角,那么A不符合题意.
B.根据邻补角的定义,B中∠1与∠2是对顶角,那么B不符合题意.
C.根据邻补角的定义,C中∠1与∠2是邻补角,那么C符合题意.
D.根据邻补角的定义,D中∠1与∠2不是邻补角,那么D不符合题意.
故选:C.
【典例8】(2022春 仓山区校级期末)如图,直线AC,BD相交于点O,∠AOB=48°,则∠COD的度数是( )
A.42° B.48° C.96° D.132°
【答案】B
【解答】解:∵∠AOB和∠COD是对顶角,
∴∠AOB=∠COD,
∵∠AOB=48°,
∴∠COD=48°.
故选:B.
【变式8-1】(2022春 来凤县期末)如图,已知直线AB与CD相交于点O,OA平分∠COE,若∠DOE=70°,则∠BOD度数是( )
A.75° B.65° C.55° D.105°
【答案】C
【解答】解:由邻补角的定义得,
∠COE=180﹣∠DOE=110°,
∵∠COE=110°且OA平分∠COE,
∴∠COA=∠AOE=55°,
∵∠COA与∠BOD是对顶角,
∴∠BOD=∠COA=55°.
故选:C.
【变式8-2】(2022春 东莞市期中)若∠A=54°,则∠A的邻补角是( )
A.36° B.126° C.46° D.136°
【答案】B
【解答】解:∠A=54°,则∠A的邻补角为180°﹣54°=126°,
故选:B.
【典例9】(2022春 和平区校级月考)如图,直线EF,CD相交于点O,OC平分∠AOF,∠AOE=2∠BOD.
(1)若∠AOE=40°,求∠DOE的度数;
(2)猜想OA与OB之间的位置关系,并证明.
【解答】解:(1)∵∠AOE=40°,
∴∠AOF=180°﹣40°=140°,
∵OC平分∠AOF,
∴∠AOC=∠COF=∠AOF,
∴∠COF=×140°=70°=∠DOE,
即∠DOE=70°;
(2)OA⊥OB,
证明:设∠BOD=α,则∠AOE=2∠BOD=2α,
∵∠AOE+∠AOF=180°,
∴∠AOF=180°﹣2α,
又∵OC平分∠AOF,
∴∠AOC=∠COF==90°﹣α,
又∵∠DOE=∠COF=90°﹣α,
∴∠BOE=∠DOE﹣∠BOD=90°﹣2α,
∴∠AOB=∠AOE+∠BOE
=2α+(90°﹣2α)
=90°,
即OA⊥OB.
【变式9-1】(2022春 碑林区校级月考)如图,直线AB与CD相交于点O,∠COE=80°,∠COF:∠AOC=2:3,射线OE平分∠BOF,求∠BOD的度数.
【解答】解:∵射线OE平分∠BOF,
∴∠BOE=∠FOE=∠BOF,
由于∠COF:∠AOC=2:3,可设∠COF=2α,则∠AOC=3α,
又∵∠COE=80°,
∴∠BOE=∠FOE=∠BOF=80°﹣2α,
∵∠AOF+∠BOF=180°,
∴5α+2(80°﹣2α)=180°,
解得α=20°,
∴∠BOD=∠AOC=3α=60°,
答:∠BOD的度数为60°
【变式9-2】(2022春 鼓楼区期中)如图,直线AB和直线CD相交于点O,OB平分∠EOD.
(1)写出图中∠BOD的对顶角 ,和两个邻补角 ;
(2)若∠BOD=40°,求∠EOC的度数.
【解答】解;(1)∠BOD的对顶角是∠AOC,两个邻补角是∠AOD,∠BOC,
故答案为:∠AOC;∠AOD,∠BOC;
(2)∵OB平分∠EOD,
∴∠DOE=2∠BOD=80°,
∵∠EOC+∠DOE=180°,
∴∠EOC=180°﹣∠DOE=100°.
【变式9-3】(2022春 东莞市期中)如图,直线AB,CD相交于O,OE是∠COB的角平分线.
(1)∠AOC的对顶角是 ;
(2)若∠BOC=130°,求∠BOD、∠DOE的度数.
【解答】解:(1)由对顶角的定义可知,∠AOC的对顶角是∠BOD,
故答案为:∠BOD;
(2)∵∠BOC=130°,∠BOC+∠BOD=180°,
∴∠BOD=180°﹣130°=50°,
又∵OE是∠COB的角平分线.
∴∠BOE=∠COE=∠BOC=65°,
∴∠DOE=∠BOD+∠BOE
=50°+65°
=115°,
答:∠DOE的度数为115°.
【学习目标】
1.理解并掌握对顶角的概念及性质,会用对顶角的性质解决一些实际问题;
2.理解并掌握补角和余角的概念及性质,会运用其解决一些实际问题.
3.理解并掌握对顶角和邻补角定义,性质,会运用其性质进行有关的运算。
【知识点梳理】
考点1 余角
(1)定义:一般地,如果两个角的和等于90°(直角),我们就说这两个角互为余角,称其中的一个角是另一个角的余角.
(2)余角的性质:同角(等角)的余角相等.
(3)数学语言表示:若∠1+∠2=90°,则∠1与∠2互余,若∠1与∠2互余,则∠1+∠2=90°.
考点2 补角
(1)定义:一般地,如果两个角的和等于180°(平角),我们就说这两个角互为补角,称其中一个角是另一个角的补角.
(2)补角的性质:同角(等角)的补角相等.
(3)数学语言表示:若∠1+∠2=180°,则∠1与∠2互补,若∠1与∠2互补,则∠1+∠2=180°.
考点3:相交线
(1)相交线概念:两条不同的直线,如有公共点则称这两条直线相交,这个公共点称为两条直线的交点。
(1)相交线的性质:两直线相交只有一个交点。
注意:(1)两条直线相交可以形成四个角。
(2)其中不超过的角称为两直线的夹角。
(3)两直线有一个交点,则两直线相交。
两线四角:两条直线相交,会出现四个角。
考点4 对顶角
(1)概念:∠1与∠3 有公共顶点O,而没有公共边,其中∠1的两边OA、OD是∠3的两边OB、OC的反向延长线,具有这种关系的两个角叫做互为对顶角。
互为对顶角:∠1=∠3, ∠2=∠4.
(2)对顶角的性质:对顶角相等
考点5 邻补角的
(1)概念:如图:∠1与∠2有一条公共边OD,它们的另外一条边为OA、OB互为反向延长线,具有这种关系的两个角叫做互为邻补角。
互为邻补角:∠1与∠2,∠2与∠3, ∠3与∠4,∠1与∠4。
(2)性质:邻补角相加180°
【典例分析】
【考点1 余角和补角及有关运算】
【典例1-1】(2022秋 思明区校级月考)已知∠α=25°30',则它的补角为( )
A.25°30′ B.64° 30' C.164° 30' D.154°30′
【典例1-2】(2022秋 泰山区校级月考)如图,已知∠BAC=90°,AD⊥BC,垂足是D,则图中与∠B互余的角有( )
A.1个 B.2个 C.3个 D.4个
【变式1-1】(2022春 舞钢市期中)若∠A=50°,则∠A的余角的度数是( )
A.40° B.130° C.90° D.180°
【变式1-1】(2021秋 重庆期末)已知∠α=35°40′,则∠α的补角的度数为( )
A.55°60′ B.55°20′ C.144°60′ D.144°20′
【变式1-3】(2022 新华区校级一模)在下列各图中,∠1与∠2一定是互补关系的是( )
A. B.
C. D.
【典例2】(2021秋 秀屿区校级期末)已知一个角的余角比它的补角的还少5°,求这个角.
【变式2-1】(2021秋 梁平区期末)若一个角的补角加上20°后等于这个角余角的3倍,则这个角的度数为( )
A.25° B.35° C.45° D.55°
【变式2-2】(2021秋 启东市期末)若一个角的余角是它的补角的,则这个角的度数是( )
A.30° B.60° C.120° D.150°
【变式2-3】(2022春 聊城期末)一个角的补角加上30°后,等于这个角的余角的4倍,则这个角的度数为( )
A.60° B.50° C.45° D.40°
【典例3】(2021秋 栾城区期末)如图,点A、O、B在同一条直线上.
(1)∠AOC比∠BOC大100°,求∠AOC与∠BOC的度数;
(2)在(1)的条件下,若∠BOC与∠BOD互余,求∠BOD的度数;
(3)在(1)(2)的条件下,若OE平分∠AOC,求∠DOE的度数.
【变式3】(2021秋 西宁期末)如图,点A,O,B在一条直线上,∠AOC=3∠COD,OE平分∠BOD.
(1)若∠COD=10°,求∠AOC的余角的度数;
(2)若∠AOC=45°,求∠COE的度数.
【典例4】(2021秋 阳东区期末)如图,将两个直角三角板的顶点叠放在一起进行探究.
(1)如图①,将一副直角三角板的直角顶点C叠放在一起,若CE恰好是∠ACB的平分线,请你猜想此时CB是不是∠ECD的平分线,并简述理由;
(2)如图②,将一副直角三角板的直角顶点C叠放在一起,若CB始终在∠DCE的内部,请猜想∠ACE与∠DCB是否相等,并简述理由;
(3)如图③,若将两个同样的三角板中60°锐角的顶点A叠放在一起,请你猜想∠DAB与∠CAE有何关系,并说明理由.
【变式4】(2021秋 泰兴市期末)将一副三角板放在同一平面内,使直角顶点重合于点O.
(1)如图①,若∠AOB=155°,则∠DOC= °,∠DOC与∠AOB的关系是 ;
(2)如图②,固定三角板BOD不动,将三角板AOC绕点O旋转到如图所示位置.
①(1)中你发现的∠DOC与∠AOB的关系是否仍然成立,请说明理由;
②如图②,若∠BOC=70°,在∠BOC内画射线OP,设∠BOP=x°(0<x<50),探究发现随着x的值的变化,图中以O为顶点的角中互余角的对数也变化.请直接写出以O为顶点的角中互余角的对数有哪几种情况?并写出每一种情况相应的x的取值或取值范围.
【考点2 相交线】
【典例5】(2022春 龙岗区校级期中)观察如图图形,并阅读相关文字:那么5条直线相交,最多交点的个数是( )
A.10 B.14 C.21 D.15
【变式5-1】(2021秋 让胡路区校级期末)如果同一平面内有三条直线,那么它们交点个数是( )个.
A.3个 B.1或3个
C.1或2或3个 D.0或1或2或3个
【变式5-2】(2022春 昭阳区校级月考)已知2条直线最多有=1个交点,3条直线最多有=3个交点,4条直线最多有=6个交点,…由此猜想,8条直线最多有个交点( )
A.16 B.28 C.32 D.40
【考点3 对顶角和邻补角及有关运算】
【典例6】(2022秋 南岗区校级月考)如图中,∠1和∠2是对顶角的是( )
A. B.
C. D.
【变式6】(2022春 江津区校级期中)下列各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
【典例7】(2022春 重庆月考)下面四个图形中,∠1与∠2是邻补角的是( )
A. B.
C. D.
【变式7】(2022春 横县期中)下列各图中,∠1与∠2是邻补角的是( )
A. B.
C. D.
【典例8】(2022春 仓山区校级期末)如图,直线AC,BD相交于点O,∠AOB=48°,则∠COD的度数是( )
A.42° B.48° C.96° D.132°
【变式8-1】(2022春 来凤县期末)如图,已知直线AB与CD相交于点O,OA平分∠COE,若∠DOE=70°,则∠BOD度数是( )
A.75° B.65° C.55° D.105°
【变式8-2】(2022春 东莞市期中)若∠A=54°,则∠A的邻补角是( )
A.36° B.126° C.46° D.136°
【典例9】(2022春 和平区校级月考)如图,直线EF,CD相交于点O,OC平分∠AOF,∠AOE=2∠BOD.
(1)若∠AOE=40°,求∠DOE的度数;
(2)猜想OA与OB之间的位置关系,并证明.
【变式9-1】(2022春 碑林区校级月考)如图,直线AB与CD相交于点O,∠COE=80°,∠COF:∠AOC=2:3,射线OE平分∠BOF,求∠BOD的度数.
【变式9-2】(2022春 鼓楼区期中)如图,直线AB和直线CD相交于点O,OB平分∠EOD.
(1)写出图中∠BOD的对顶角 ,和两个邻补角 ;
(2)若∠BOD=40°,求∠EOC的度数.
【变式9-3】(2022春 东莞市期中)如图,直线AB,CD相交于O,OE是∠COB的角平分线.
(1)∠AOC的对顶角是 ;
(2)若∠BOC=130°,求∠BOD、∠DOE的度数.
专题6.3 余角、补角、对顶角(知识解读)
【学习目标】
1.理解并掌握对顶角的概念及性质,会用对顶角的性质解决一些实际问题;
2.理解并掌握补角和余角的概念及性质,会运用其解决一些实际问题.
3.理解并掌握对顶角和邻补角定义,性质,会运用其性质进行有关的运算。
【知识点梳理】
考点1 余角
(1)定义:一般地,如果两个角的和等于90°(直角),我们就说这两个角互为余角,称其中的一个角是另一个角的余角.
(2)余角的性质:同角(等角)的余角相等.
(3)数学语言表示:若∠1+∠2=90°,则∠1与∠2互余,若∠1与∠2互余,则∠1+∠2=90°.
考点2 补角
(1)定义:一般地,如果两个角的和等于180°(平角),我们就说这两个角互为补角,称其中一个角是另一个角的补角.
(2)补角的性质:同角(等角)的补角相等.
(3)数学语言表示:若∠1+∠2=180°,则∠1与∠2互补,若∠1与∠2互补,则∠1+∠2=180°.
考点3:相交线
(1)相交线概念:两条不同的直线,如有公共点则称这两条直线相交,这个公共点称为两条直线的交点。
(1)相交线的性质:两直线相交只有一个交点。
注意:(1)两条直线相交可以形成四个角。
(2)其中不超过的角称为两直线的夹角。
(3)两直线有一个交点,则两直线相交。
两线四角:两条直线相交,会出现四个角。
考点4 对顶角
(1)概念:∠1与∠3 有公共顶点O,而没有公共边,其中∠1的两边OA、OD是∠3的两边OB、OC的反向延长线,具有这种关系的两个角叫做互为对顶角。
互为对顶角:∠1=∠3, ∠2=∠4.
(2)对顶角的性质:对顶角相等
考点5 邻补角的
(1)概念:如图:∠1与∠2有一条公共边OD,它们的另外一条边为OA、OB互为反向延长线,具有这种关系的两个角叫做互为邻补角。
互为邻补角:∠1与∠2,∠2与∠3, ∠3与∠4,∠1与∠4。
(2)性质:邻补角相加180°
【典例分析】
【考点1 余角和补角及有关运算】
【典例1-1】(2022秋 思明区校级月考)已知∠α=25°30',则它的补角为( )
A.25°30′ B.64° 30' C.164° 30' D.154°30′
【答案】D
【解答】解:180°﹣25°30′=154°30′.
故选:D.
【典例1-2】(2022秋 泰山区校级月考)如图,已知∠BAC=90°,AD⊥BC,垂足是D,则图中与∠B互余的角有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【解答】解:∵∠BAC=90°,
∴∠ABD+∠C=90°;
又∵AD⊥BC,
∴∠BDA=90°,
∴∠B+∠BAD=90°,
故图中与∠B互余的角有2个.
故选:B.
【变式1-1】(2022春 舞钢市期中)若∠A=50°,则∠A的余角的度数是( )
A.40° B.130° C.90° D.180°
【答案】A
【解答】解:∠A的余角=90°﹣50°=40°.
故答案为:A.
【变式1-1】(2021秋 重庆期末)已知∠α=35°40′,则∠α的补角的度数为( )
A.55°60′ B.55°20′ C.144°60′ D.144°20′
【答案】D
【解答】解:∵∠α=35°40′,
∴∠α的补角的度数为180°﹣35°40′=144°20′.
故选:D.
【变式1-3】(2022 新华区校级一模)在下列各图中,∠1与∠2一定是互补关系的是( )
A. B.
C. D.
【答案】B
【解答】解:对于A选项,∠1与∠2为对顶角,
∴∠1=∠2,不一定是互补关系,
故A选项错误;
对于B选项,由平角的定义可得∠1+∠2=180°,
∴∠1与∠2是互补关系,
故B选项正确;
对于C选项,根据三角形内角和定理可知,
∠1+∠2=90°,
∴∠1与∠2是互余关系,
故C选项错误;
对于D选项,∠1与∠2为同旁内角,
当两直线平行时,∠1与∠2互补,否则不一定互补,
故D选项错误.
故选:B.
【典例2】(2021秋 秀屿区校级期末)已知一个角的余角比它的补角的还少5°,求这个角.
【解答】解:设这个角的度数是x°,
则90﹣x=(180﹣x)﹣5,
解得:x=27,
即这个角的度数是27°,
答:这个角的度数是27°.
【变式2-1】(2021秋 梁平区期末)若一个角的补角加上20°后等于这个角余角的3倍,则这个角的度数为( )
A.25° B.35° C.45° D.55°
【答案】B
【解答】解:设这个角为x,则它的余角为90°﹣x,补角180°﹣x,
根据题意得,180°﹣x+20°=3(90°﹣x),
解得x=35°.
故选:B.
【变式2-2】(2021秋 启东市期末)若一个角的余角是它的补角的,则这个角的度数是( )
A.30° B.60° C.120° D.150°
【答案】A
【解答】解:设这个角为α,则它的余角为90°﹣α,它的补角为180°﹣α.
由题意得,90°﹣α=(180°﹣α),
解得:α=30°.
故这个角的度数为30°.
故选:A.
【变式2-3】(2022春 聊城期末)一个角的补角加上30°后,等于这个角的余角的4倍,则这个角的度数为( )
A.60° B.50° C.45° D.40°
【答案】B
【解答】解:设这个角的度数为x.
由题意得,180°﹣x+30°=4(90°﹣x).
∴x=50°.
故选:B
【典例3】(2021秋 栾城区期末)如图,点A、O、B在同一条直线上.
(1)∠AOC比∠BOC大100°,求∠AOC与∠BOC的度数;
(2)在(1)的条件下,若∠BOC与∠BOD互余,求∠BOD的度数;
(3)在(1)(2)的条件下,若OE平分∠AOC,求∠DOE的度数.
【解答】解:(1)∵∠AOC比∠BOC大100°,
∴∠AOC=∠BOC+100°,
又点A、O、B在同一条直线上.
∴∠AOC+∠BOC=180°,
∴∠BOC+100°+∠BOC=180°,
∴∠BOC=40°,
∠AOC=140°;
(2)∵∠BOC与∠BOD互余,
∴∠BOD+∠BOC=90°,
∴∠BOD=90°﹣∠BOC=90°﹣40°=50°;
(3)∵OE平分∠AOC,
∴得∠COE=∠AOC=70°,
∵∠BOD+∠BOC=90°,
∴∠DOE=∠COE+∠COD=∠COE+∠BOD+∠BOC
=70°+90°
=160°.
【变式3】(2021秋 西宁期末)如图,点A,O,B在一条直线上,∠AOC=3∠COD,OE平分∠BOD.
(1)若∠COD=10°,求∠AOC的余角的度数;
(2)若∠AOC=45°,求∠COE的度数.
【解答】解:(1)∵∠AOC=3∠COD,∠COD=10°,
∴∠AOC=30°,
∴∠AOC的余角=90°﹣30°=60°,
∴∠AOC的余角的度数是60°;
(2)∵∠AOC=3∠COD,∠AOC=45°,
∴,
∵点A,O,B在一条直线上,
∴∠AOB=180°,
∴∠BOD=180°﹣∠AOC﹣∠COD=180°﹣45°﹣15°=120°,
∵OE平分∠BOD,
∴,
∴∠COE=∠COD+∠DOE=15°+60°=75°,
∴∠COE的度数为75°.
【典例4】(2021秋 阳东区期末)如图,将两个直角三角板的顶点叠放在一起进行探究.
(1)如图①,将一副直角三角板的直角顶点C叠放在一起,若CE恰好是∠ACB的平分线,请你猜想此时CB是不是∠ECD的平分线,并简述理由;
(2)如图②,将一副直角三角板的直角顶点C叠放在一起,若CB始终在∠DCE的内部,请猜想∠ACE与∠DCB是否相等,并简述理由;
(3)如图③,若将两个同样的三角板中60°锐角的顶点A叠放在一起,请你猜想∠DAB与∠CAE有何关系,并说明理由.
【解答】解:(1)CB是∠ECD的平分线,
理由:∵∠ACB=90°,CE是∠ACB的平分线,
∴∠ECB=∠ACB=45°,
∴∠DCB=∠ECD﹣∠ECB=90°﹣45°=45°,
∴∠ECB=∠DCB,
∴CB是∠ECD的平分线;
(2)∠ACE=∠DCB,
理由:∵∠ACB=∠DCE=90°,
∴∠ACE+∠ECB=90°,∠DCB+∠ECB=90°,
∴∠ACE=∠DCB;
(3)∠DAB+∠EAC=120°,
理由:∵∠DAC=∠EAB=60°,
∴∠DAE+∠EAC=60°,∠EAC+∠CAB=60°,
∴∠DAE+∠EAC+∠EAC+∠CAB=120°,
∵∠DAE+∠EAC+∠CAB=∠DAB,
∴∠DAB+∠CAE=120°.
【变式4】(2021秋 泰兴市期末)将一副三角板放在同一平面内,使直角顶点重合于点O.
(1)如图①,若∠AOB=155°,则∠DOC= °,∠DOC与∠AOB的关系是 ;
(2)如图②,固定三角板BOD不动,将三角板AOC绕点O旋转到如图所示位置.
①(1)中你发现的∠DOC与∠AOB的关系是否仍然成立,请说明理由;
②如图②,若∠BOC=70°,在∠BOC内画射线OP,设∠BOP=x°(0<x<50),探究发现随着x的值的变化,图中以O为顶点的角中互余角的对数也变化.请直接写出以O为顶点的角中互余角的对数有哪几种情况?并写出每一种情况相应的x的取值或取值范围.
【解答】解:(1)由题意可知,∠AOC=∠BOD=90°,
∵∠AOB=155°,
∴∠COD=360°﹣∠AOC﹣∠BOD﹣∠AOB=25°,
∴∠AOB+∠COD=155°+25°=180°;
故答案为:25;互补;
(2)①成立;
理由:∠DOC+∠AOB
=∠AOC﹣∠AOD+∠DOB+∠AOD
=∠AOC+∠DOB
=90°+90°
=180°;
②∵∠BOC=70°,
∴∠COD=20°,
∴∠AOD=70°;此时有两对角互余,∠AOD和∠COD,∠BOC和∠COD;
当共有3种情况:
当x=35时,∠BOP=∠COP=35°,则∠BOP+∠DOP=∠COP+∠DOP=90°,
此时互余的角有4对:∠AOD和∠COD,∠BOC和∠COD,∠BOP和∠DOP,∠COP和∠DOP;
当x=20时,∠BOC=∠AOD=∠DOP=70°,∠COD=∠COP=20°,
此时,互余的角有6对:∠AOD和∠COD,∠BOC和∠COD,∠DOP和∠COD,∠AOD和∠BOP,∠BOC和∠BOP,∠DOP和∠BOP;
当0<x<50且x≠35和20时,
此时互余的角有3对:∠AOD和∠COD,∠BOC和∠COD,∠BOP和∠DOP.
【考点2 相交线】
【典例5】(2022春 龙岗区校级期中)观察如图图形,并阅读相关文字:那么5条直线相交,最多交点的个数是( )
A.10 B.14 C.21 D.15
【答案】A
【解答】解:两条直线相交,最多交点数为1个;
三条直线相交,最多交点数为1+2=3(个);
四条直线相交,最多交点数为1+2+3=6(个);
五条直线相交,最多交点数为1+2+3+4=10(个).
故选:A.
【变式5-1】(2021秋 让胡路区校级期末)如果同一平面内有三条直线,那么它们交点个数是( )个.
A.3个 B.1或3个
C.1或2或3个 D.0或1或2或3个
【答案】D
【解答】解:当三条直线平行时,交点个数为0;
当三条直线相交于1点时,交点个数为1;
当三条直线中,有两条平行,另一条分别与他们相交时,交点个数为2;
当三条直线互相不平行时,交点个数为3;
所以,它们的交点个数有4种情形.
故选:D.
【变式5-2】(2022春 昭阳区校级月考)已知2条直线最多有=1个交点,3条直线最多有=3个交点,4条直线最多有=6个交点,…由此猜想,8条直线最多有个交点( )
A.16 B.28 C.32 D.40
【答案】B
【解答】解:∵2条直线最多有=1个交点,
3条直线最多有=3个交点,
4条直线最多有=6个交点,
……
n条直线最多有个交点,
∴n=8时,==28.
故选:B
【考点3 对顶角和邻补角及有关运算】
【典例6】(2022秋 南岗区校级月考)如图中,∠1和∠2是对顶角的是( )
A. B.
C. D.
【答案】B
【解答】解:由对顶角的定义可知,
图中的∠1与∠2是对顶角,
故选:B.
【变式6】(2022春 江津区校级期中)下列各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
【答案】C
【解答】解:根据对顶角的定义可知:只有C选项中的是对顶角,其它都不是.
故选:C.
【典例7】(2022春 重庆月考)下面四个图形中,∠1与∠2是邻补角的是( )
A. B.
C. D.
【答案】C
【解答】解:根据邻补角的定义可知,
图中的∠1与∠2是邻补角,
故选:C.
【变式7】(2022春 横县期中)下列各图中,∠1与∠2是邻补角的是( )
A. B.
C. D.
【答案】C
【解答】解:A.根据邻补角的定义,A中∠1与∠2不是邻补角,那么A不符合题意.
B.根据邻补角的定义,B中∠1与∠2是对顶角,那么B不符合题意.
C.根据邻补角的定义,C中∠1与∠2是邻补角,那么C符合题意.
D.根据邻补角的定义,D中∠1与∠2不是邻补角,那么D不符合题意.
故选:C.
【典例8】(2022春 仓山区校级期末)如图,直线AC,BD相交于点O,∠AOB=48°,则∠COD的度数是( )
A.42° B.48° C.96° D.132°
【答案】B
【解答】解:∵∠AOB和∠COD是对顶角,
∴∠AOB=∠COD,
∵∠AOB=48°,
∴∠COD=48°.
故选:B.
【变式8-1】(2022春 来凤县期末)如图,已知直线AB与CD相交于点O,OA平分∠COE,若∠DOE=70°,则∠BOD度数是( )
A.75° B.65° C.55° D.105°
【答案】C
【解答】解:由邻补角的定义得,
∠COE=180﹣∠DOE=110°,
∵∠COE=110°且OA平分∠COE,
∴∠COA=∠AOE=55°,
∵∠COA与∠BOD是对顶角,
∴∠BOD=∠COA=55°.
故选:C.
【变式8-2】(2022春 东莞市期中)若∠A=54°,则∠A的邻补角是( )
A.36° B.126° C.46° D.136°
【答案】B
【解答】解:∠A=54°,则∠A的邻补角为180°﹣54°=126°,
故选:B.
【典例9】(2022春 和平区校级月考)如图,直线EF,CD相交于点O,OC平分∠AOF,∠AOE=2∠BOD.
(1)若∠AOE=40°,求∠DOE的度数;
(2)猜想OA与OB之间的位置关系,并证明.
【解答】解:(1)∵∠AOE=40°,
∴∠AOF=180°﹣40°=140°,
∵OC平分∠AOF,
∴∠AOC=∠COF=∠AOF,
∴∠COF=×140°=70°=∠DOE,
即∠DOE=70°;
(2)OA⊥OB,
证明:设∠BOD=α,则∠AOE=2∠BOD=2α,
∵∠AOE+∠AOF=180°,
∴∠AOF=180°﹣2α,
又∵OC平分∠AOF,
∴∠AOC=∠COF==90°﹣α,
又∵∠DOE=∠COF=90°﹣α,
∴∠BOE=∠DOE﹣∠BOD=90°﹣2α,
∴∠AOB=∠AOE+∠BOE
=2α+(90°﹣2α)
=90°,
即OA⊥OB.
【变式9-1】(2022春 碑林区校级月考)如图,直线AB与CD相交于点O,∠COE=80°,∠COF:∠AOC=2:3,射线OE平分∠BOF,求∠BOD的度数.
【解答】解:∵射线OE平分∠BOF,
∴∠BOE=∠FOE=∠BOF,
由于∠COF:∠AOC=2:3,可设∠COF=2α,则∠AOC=3α,
又∵∠COE=80°,
∴∠BOE=∠FOE=∠BOF=80°﹣2α,
∵∠AOF+∠BOF=180°,
∴5α+2(80°﹣2α)=180°,
解得α=20°,
∴∠BOD=∠AOC=3α=60°,
答:∠BOD的度数为60°
【变式9-2】(2022春 鼓楼区期中)如图,直线AB和直线CD相交于点O,OB平分∠EOD.
(1)写出图中∠BOD的对顶角 ,和两个邻补角 ;
(2)若∠BOD=40°,求∠EOC的度数.
【解答】解;(1)∠BOD的对顶角是∠AOC,两个邻补角是∠AOD,∠BOC,
故答案为:∠AOC;∠AOD,∠BOC;
(2)∵OB平分∠EOD,
∴∠DOE=2∠BOD=80°,
∵∠EOC+∠DOE=180°,
∴∠EOC=180°﹣∠DOE=100°.
【变式9-3】(2022春 东莞市期中)如图,直线AB,CD相交于O,OE是∠COB的角平分线.
(1)∠AOC的对顶角是 ;
(2)若∠BOC=130°,求∠BOD、∠DOE的度数.
【解答】解:(1)由对顶角的定义可知,∠AOC的对顶角是∠BOD,
故答案为:∠BOD;
(2)∵∠BOC=130°,∠BOC+∠BOD=180°,
∴∠BOD=180°﹣130°=50°,
又∵OE是∠COB的角平分线.
∴∠BOE=∠COE=∠BOC=65°,
∴∠DOE=∠BOD+∠BOE
=50°+65°
=115°,
答:∠DOE的度数为115°.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
