第二十六章 反比例函数章末复习课件 (共29张PPT)
文档属性
| 名称 | 第二十六章 反比例函数章末复习课件 (共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 19:52:55 | ||
图片预览








文档简介
(共29张PPT)
第二十六章 反比例函数
章末复习
反比例函数是学习了一次函数后我们接触的又一最基本的函数.考试试卷中与反比例函数有关的试题一般属于中档题,少量出现在压轴题中,题型多样,时时出新,有一定的综合性,所以我们要给予足够的重视.
1. 反比例函数的概念
形如________ (k为常数,k≠0) 的函数称为反比例函数,其中x是自变量,y是x的函数,k是比例系数.
三种表达式方法:
特别注意:(1)k≠0;(2)自变量x≠0;(3)函数y≠0.
或 xy=kx 或y=kx-1 (k≠0).
反比例函数的两条对称轴为直线 和 ;
对称中心是:
(1) 反比例函数的图象:反比例函数 (k≠0)的图象是 ,它既是轴对称图形又是中心对称图形.
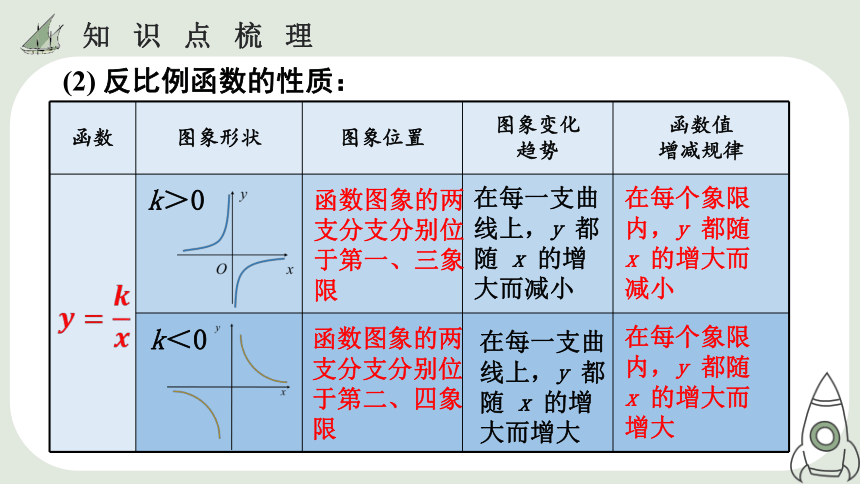
2. 反比例函数的图象和性质
双曲线
原点
y = x
y=-x
函数 图象形状 图象位置 图象变化
趋势 函数值
增减规律
在每个象限内,y 都随 x 的增大而减小
在每个象限内,y 都随 x 的增大而增大
函数图象的两支分支分别位于第一、三象限
函数图象的两支分支分别位于第二、四象限
k>0
k<0
在每一支曲线上,y 都随 x 的增大而减小
在每一支曲线上,y 都随 x 的增大而增大
(2) 反比例函数的性质:
(3) 反比例函数比例系数 k 的几何意义
k 的几何意义:反比例函数图象上的点 (x,y) 具有两坐标之积 (xy=k) 为常数这一特点,即过双曲线上任意一点,向两坐标轴作垂线,两条垂线与坐标轴所围成的矩形的面积为常数 |k|.
规律:过双曲线上任意一点,向两坐标轴作垂线,一条垂线与坐标轴、原点所围成的三角形的面积为常数 .
3. 反比例函数的应用
(1)待定系数法:
①设(设出含有待定系数的反比例函数解析式);
②代(将已知条件(自变量与函数的对应值)代入解析式,得到关于待定系数的方程);
③解(解方程,求出待定系数);
④写(写出反比例函数解析式).
过程:
分析实际情境→建立函数模型→明确数学问题
特别注意:自变量和因变量的取值范围(往往都
取非负数).
(2) 反比例函数解决实际问题:
练习1. 下列函数中哪些是正比例函数?哪些是反比例函数
① y = 3x-1
② y = 2x2
⑤ y = 3x
③
④
⑥
⑦
⑧
练习2. 已知点 P(1,-3) 在反比例函数 的图象上,
则 k 的值是 ( )
A. 3 B. -3
C. D.
B
练习3. 若 是反比例函数,则 a 的值为 ( )
A. 1 B. -1 C. ±1 D. 任意实数
A
练习4 已知点 A(1,y1),B(2,y2),C(-3,y3) 都在反比
例函数 的图象上,则y1,y2,y3的大小关系是
( )
A. y3<y1<y2 B. y1<y2<y3
C. y2<y1<y3 D. y3<y2<y1
分析:方法①:分别把各点代入反比例函数求出y1,y2,y3的值,再比较出其大小即可.
方法②:根据反比例函数的图象和性质比较.
D
y1 >0>y2
练习5 已知点 A (x1,y1),B (x2,y2) (x1<0<x2)都在反比例函数 (k<0) 的图象上,则 y1 与 y2 的大小关系 (从大到小) 为 .
练习6 如图,两个反比例函数 和 的图象分别是 l1 和 l2.设点 P 在 l1 上,PC⊥x 轴,垂足为 C,交 l2 于点 A;PD⊥y 轴,垂足为 D,交l2 于点 B,则△PAB 的面积为( ).
A.3 B.4 C. D.5
x
y
P
A
O
B
C
D
l2
l1
C
练习7 如图,两个反比例函数 和 在第一象
限内的图象分别是 C1 和 C2,设点 P 在 C1 上,PA ⊥
x 轴于点A,交C2于点B,则△POB的面积为 .
1
练习7 如图,在平面直角坐标系中,点 M 为 x 轴正半轴 上 一点,过点 M 的直线 l∥ y 轴,且直线 l 分别与反比 例函数 (x>0)和 (x>0) 的图象交于P,Q 两点,若 S△POQ=14,则 k 的值为 .
20
4
10
练习8 如图,已知点 A,B 在双曲线 上,AC⊥x 轴于点C,BD⊥y 轴于点 D,AC 与 BD 交于点 P,P 是 AC 的中点,若△ABP 的面积为6,则 k = .
24
E
F
解析:S△ABP= S四边形BFCP
= (S四边形BDOF-S四边形OCPD)
= (S四边形BDOF- S四边形AEOC)
= (k- k)= k = 6
∴ k =24.
练习9 如图,已知 A (-4, ),B (-1,2) 是一次函数y =kx+b 与反比例函数 (m<0)图象的两个交点,AC⊥x 轴于点 C,BD⊥y 轴于点 D.
(1) 根据图象直接回答:在第二象限内,当 x 取何值
时,一次函数的值大于反比例函数的值;
O
B
A
x
y
C
D
解:当-4< x <-1时,一
次函数的值大于反比例
函数的值.
(2) 求一次函数解析式及 m 的值;
解:把A(-4, ),B(-1,2)代入 y = kx + b中,得
-4k + b = ,
-k + b =2,
解得
k = ,
b = ,
所以一次函数的解析式为 y = x + .
把 B (-1,2)代入 中,得 m =-1×2=-2.
(3) P 是线段 AB 上的一点,连接 PC,PD,若△PCA和 △PDB 面积相等,求点 P 坐标.
O
B
A
x
y
C
D
P
解:设点 P 的坐标为 ( t, t + ),
P点到直线 AC 的距离为 t-(-4),
P 点到直线 BD 的距离为2- ( t+ ).
∵ △PCA面积和△PDB面积相等,
∴ AC·[t-(-4)]= BD·[2-[ 2-( t+ )],
解得:t = .
∴ 点 P 的坐标为 ( , ).
练习10 病人按规定的剂量服用某种药物,测得服药后 2 小时,每毫升血液中的含药量达到最大值为 4 毫克. 已知服药后,2 小时前每毫升血液中的含药量 y (单位:毫克)与时间 x (单位:小时) 成正比例;2 小时后 y 与 x 成反比例 (如图). 根据以上信息解答下列问题:
(1) 求当 0 ≤ x ≤2 时,y 与 x 的函数解析式;
解:当 0 ≤ x ≤2 时,y 与 x 成正比
例函数关系.
设 y =kx,由于点 (2,4) 在
线段上,
所以 4=2k,k=2,即 y=2x.
O
y/毫克
x/小时
2
4
(2) 求当 x > 2 时,y 与 x 的函数解析式;
解:当 x > 2时,y 与 x 成反比例函数关系,
设
解得 k =8.
由于点 (2,4) 在反比例函数的图象上,
所以
即
O
y/毫克
x/小时
2
4
(3) 若每毫升血液中的含药量不低于 2 毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?
解:当 0≤x≤2 时,含药量不低于 2 毫克,即 2x≥2,
解得x≥1,∴1≤x≤2;
当 x>2 时,含药量不低于 2 毫克,
即 ≥ 2,解得 x ≤ 4. ∴2< x ≤4.
所以服药一次,治疗疾病的有
效时间是1+2=3 (小时).
O
y/毫克
x/小时
2
4
练习11 如图,一块砖的 A,B,C 三个面的面积比是4∶2∶1.如果B 面向下放在地上,地面所受压强为a Pa,那么 A 面和 C 面分别向下放在地上时,地面所受压强各是多少?
解:设A、B、C三个面的面积分别为4S,2S,S,砖的重力为G.
据题意:,则G = 2aS.
∴ 把A面向下放在地上,地面所受压强为
把C面向下放在地上,地面所受压强为
练习12 已知某品牌显示器的寿命大约为2×104 h.
(1)这种显示器可工作的天数 d 与平均每日工作的小时数 t 之间具有怎样的函数关系?
(2)如果平均每天工作10 h,那么这种显示器大约可使用多长时间?
因此这种显示器大约可使用2×103天.
解
练习13.市政府计划建设一项水利工程,工程需要运送的土石方总量为106m3,某运输公司承办了该项工程运送土石方的任务.
(1)运输公司平均每天的工作量v(m3/天)与完成运送任务所需的时间t(天)之间有怎样的函数关系?
(2)这个运输公司共有100辆卡车,每天一共可运送土石方104m3,则公司完成全部运输任务需要多长时间?
(3)当公司以问题(2)中的速度工作了40天后,由于工程进度的需要,剩下的所有运输任务必须在50天内完成,公司至少需要再增加多少辆卡车才能按时完成任务?
解
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第二十六章 反比例函数
章末复习
反比例函数是学习了一次函数后我们接触的又一最基本的函数.考试试卷中与反比例函数有关的试题一般属于中档题,少量出现在压轴题中,题型多样,时时出新,有一定的综合性,所以我们要给予足够的重视.
1. 反比例函数的概念
形如________ (k为常数,k≠0) 的函数称为反比例函数,其中x是自变量,y是x的函数,k是比例系数.
三种表达式方法:
特别注意:(1)k≠0;(2)自变量x≠0;(3)函数y≠0.
或 xy=kx 或y=kx-1 (k≠0).
反比例函数的两条对称轴为直线 和 ;
对称中心是:
(1) 反比例函数的图象:反比例函数 (k≠0)的图象是 ,它既是轴对称图形又是中心对称图形.
2. 反比例函数的图象和性质
双曲线
原点
y = x
y=-x
函数 图象形状 图象位置 图象变化
趋势 函数值
增减规律
在每个象限内,y 都随 x 的增大而减小
在每个象限内,y 都随 x 的增大而增大
函数图象的两支分支分别位于第一、三象限
函数图象的两支分支分别位于第二、四象限
k>0
k<0
在每一支曲线上,y 都随 x 的增大而减小
在每一支曲线上,y 都随 x 的增大而增大
(2) 反比例函数的性质:
(3) 反比例函数比例系数 k 的几何意义
k 的几何意义:反比例函数图象上的点 (x,y) 具有两坐标之积 (xy=k) 为常数这一特点,即过双曲线上任意一点,向两坐标轴作垂线,两条垂线与坐标轴所围成的矩形的面积为常数 |k|.
规律:过双曲线上任意一点,向两坐标轴作垂线,一条垂线与坐标轴、原点所围成的三角形的面积为常数 .
3. 反比例函数的应用
(1)待定系数法:
①设(设出含有待定系数的反比例函数解析式);
②代(将已知条件(自变量与函数的对应值)代入解析式,得到关于待定系数的方程);
③解(解方程,求出待定系数);
④写(写出反比例函数解析式).
过程:
分析实际情境→建立函数模型→明确数学问题
特别注意:自变量和因变量的取值范围(往往都
取非负数).
(2) 反比例函数解决实际问题:
练习1. 下列函数中哪些是正比例函数?哪些是反比例函数
① y = 3x-1
② y = 2x2
⑤ y = 3x
③
④
⑥
⑦
⑧
练习2. 已知点 P(1,-3) 在反比例函数 的图象上,
则 k 的值是 ( )
A. 3 B. -3
C. D.
B
练习3. 若 是反比例函数,则 a 的值为 ( )
A. 1 B. -1 C. ±1 D. 任意实数
A
练习4 已知点 A(1,y1),B(2,y2),C(-3,y3) 都在反比
例函数 的图象上,则y1,y2,y3的大小关系是
( )
A. y3<y1<y2 B. y1<y2<y3
C. y2<y1<y3 D. y3<y2<y1
分析:方法①:分别把各点代入反比例函数求出y1,y2,y3的值,再比较出其大小即可.
方法②:根据反比例函数的图象和性质比较.
D
y1 >0>y2
练习5 已知点 A (x1,y1),B (x2,y2) (x1<0<x2)都在反比例函数 (k<0) 的图象上,则 y1 与 y2 的大小关系 (从大到小) 为 .
练习6 如图,两个反比例函数 和 的图象分别是 l1 和 l2.设点 P 在 l1 上,PC⊥x 轴,垂足为 C,交 l2 于点 A;PD⊥y 轴,垂足为 D,交l2 于点 B,则△PAB 的面积为( ).
A.3 B.4 C. D.5
x
y
P
A
O
B
C
D
l2
l1
C
练习7 如图,两个反比例函数 和 在第一象
限内的图象分别是 C1 和 C2,设点 P 在 C1 上,PA ⊥
x 轴于点A,交C2于点B,则△POB的面积为 .
1
练习7 如图,在平面直角坐标系中,点 M 为 x 轴正半轴 上 一点,过点 M 的直线 l∥ y 轴,且直线 l 分别与反比 例函数 (x>0)和 (x>0) 的图象交于P,Q 两点,若 S△POQ=14,则 k 的值为 .
20
4
10
练习8 如图,已知点 A,B 在双曲线 上,AC⊥x 轴于点C,BD⊥y 轴于点 D,AC 与 BD 交于点 P,P 是 AC 的中点,若△ABP 的面积为6,则 k = .
24
E
F
解析:S△ABP= S四边形BFCP
= (S四边形BDOF-S四边形OCPD)
= (S四边形BDOF- S四边形AEOC)
= (k- k)= k = 6
∴ k =24.
练习9 如图,已知 A (-4, ),B (-1,2) 是一次函数y =kx+b 与反比例函数 (m<0)图象的两个交点,AC⊥x 轴于点 C,BD⊥y 轴于点 D.
(1) 根据图象直接回答:在第二象限内,当 x 取何值
时,一次函数的值大于反比例函数的值;
O
B
A
x
y
C
D
解:当-4< x <-1时,一
次函数的值大于反比例
函数的值.
(2) 求一次函数解析式及 m 的值;
解:把A(-4, ),B(-1,2)代入 y = kx + b中,得
-4k + b = ,
-k + b =2,
解得
k = ,
b = ,
所以一次函数的解析式为 y = x + .
把 B (-1,2)代入 中,得 m =-1×2=-2.
(3) P 是线段 AB 上的一点,连接 PC,PD,若△PCA和 △PDB 面积相等,求点 P 坐标.
O
B
A
x
y
C
D
P
解:设点 P 的坐标为 ( t, t + ),
P点到直线 AC 的距离为 t-(-4),
P 点到直线 BD 的距离为2- ( t+ ).
∵ △PCA面积和△PDB面积相等,
∴ AC·[t-(-4)]= BD·[2-[ 2-( t+ )],
解得:t = .
∴ 点 P 的坐标为 ( , ).
练习10 病人按规定的剂量服用某种药物,测得服药后 2 小时,每毫升血液中的含药量达到最大值为 4 毫克. 已知服药后,2 小时前每毫升血液中的含药量 y (单位:毫克)与时间 x (单位:小时) 成正比例;2 小时后 y 与 x 成反比例 (如图). 根据以上信息解答下列问题:
(1) 求当 0 ≤ x ≤2 时,y 与 x 的函数解析式;
解:当 0 ≤ x ≤2 时,y 与 x 成正比
例函数关系.
设 y =kx,由于点 (2,4) 在
线段上,
所以 4=2k,k=2,即 y=2x.
O
y/毫克
x/小时
2
4
(2) 求当 x > 2 时,y 与 x 的函数解析式;
解:当 x > 2时,y 与 x 成反比例函数关系,
设
解得 k =8.
由于点 (2,4) 在反比例函数的图象上,
所以
即
O
y/毫克
x/小时
2
4
(3) 若每毫升血液中的含药量不低于 2 毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?
解:当 0≤x≤2 时,含药量不低于 2 毫克,即 2x≥2,
解得x≥1,∴1≤x≤2;
当 x>2 时,含药量不低于 2 毫克,
即 ≥ 2,解得 x ≤ 4. ∴2< x ≤4.
所以服药一次,治疗疾病的有
效时间是1+2=3 (小时).
O
y/毫克
x/小时
2
4
练习11 如图,一块砖的 A,B,C 三个面的面积比是4∶2∶1.如果B 面向下放在地上,地面所受压强为a Pa,那么 A 面和 C 面分别向下放在地上时,地面所受压强各是多少?
解:设A、B、C三个面的面积分别为4S,2S,S,砖的重力为G.
据题意:,则G = 2aS.
∴ 把A面向下放在地上,地面所受压强为
把C面向下放在地上,地面所受压强为
练习12 已知某品牌显示器的寿命大约为2×104 h.
(1)这种显示器可工作的天数 d 与平均每日工作的小时数 t 之间具有怎样的函数关系?
(2)如果平均每天工作10 h,那么这种显示器大约可使用多长时间?
因此这种显示器大约可使用2×103天.
解
练习13.市政府计划建设一项水利工程,工程需要运送的土石方总量为106m3,某运输公司承办了该项工程运送土石方的任务.
(1)运输公司平均每天的工作量v(m3/天)与完成运送任务所需的时间t(天)之间有怎样的函数关系?
(2)这个运输公司共有100辆卡车,每天一共可运送土石方104m3,则公司完成全部运输任务需要多长时间?
(3)当公司以问题(2)中的速度工作了40天后,由于工程进度的需要,剩下的所有运输任务必须在50天内完成,公司至少需要再增加多少辆卡车才能按时完成任务?
解
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
