数学人教A版(2019)选择性必修第一册3.2.2双曲线的简单几何性质(共27张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册3.2.2双曲线的简单几何性质(共27张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 32.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
第三章
圆锥曲线
3.2.2双曲线的简单几何性质
一
二
三
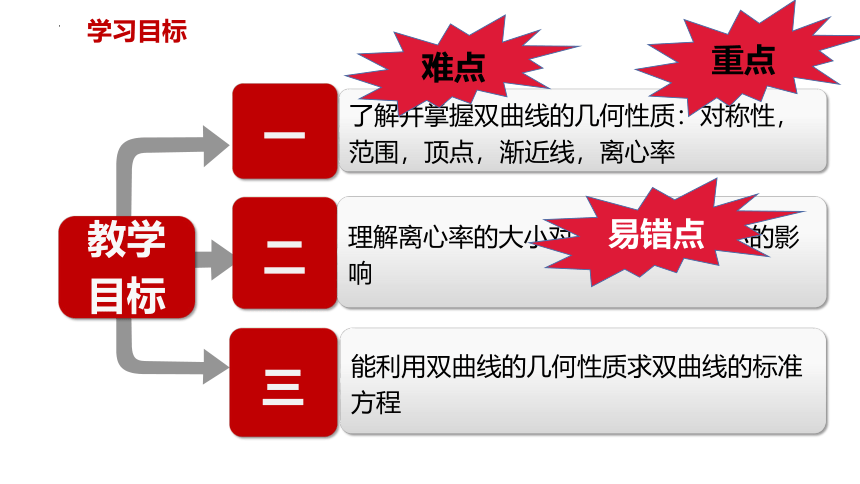
教学目标
了解并掌握双曲线的几何性质:对称性,范围,顶点,渐近线,离心率
理解离心率的大小对双曲线开口大小的影响
能利用双曲线的几何性质求双曲线的标准方程
学习目标
难点
重点
易错点
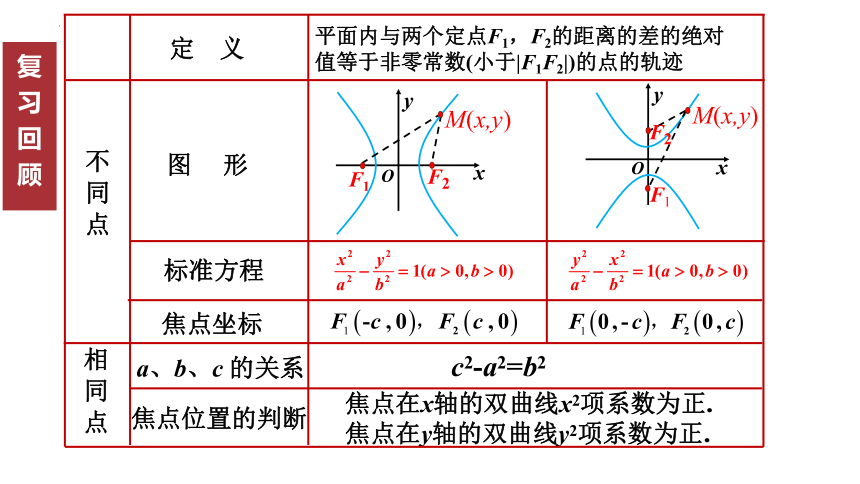
复习回顾
焦点在x轴的双曲线x2项系数为正.
焦点在y轴的双曲线y2项系数为正.
标准方程
相 同 点
焦点位置的判断
不 同 点
图 形
焦点坐标
定 义
a、b、c 的关系
c2-a2=b2
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹
x
F1
F2
y
O
M(x,y)
x
y
O
M(x,y)
F1
F2
新课导入
问题1类比对椭圆几何性质的研究,你认为应该研究双曲线
的哪些几何性质?如何研究这些性质?
范围、对称性、顶点、离心率
渐近线
下面,我们利用双曲线的标准方程
研究双曲线的几何性质.
新知探究
探究一:观察的形状,提炼出它的几何性质
观察双曲线 的形状, 你能从图上看出它的范围吗 它具有什么样的对称性 双曲线上哪些点比较特殊
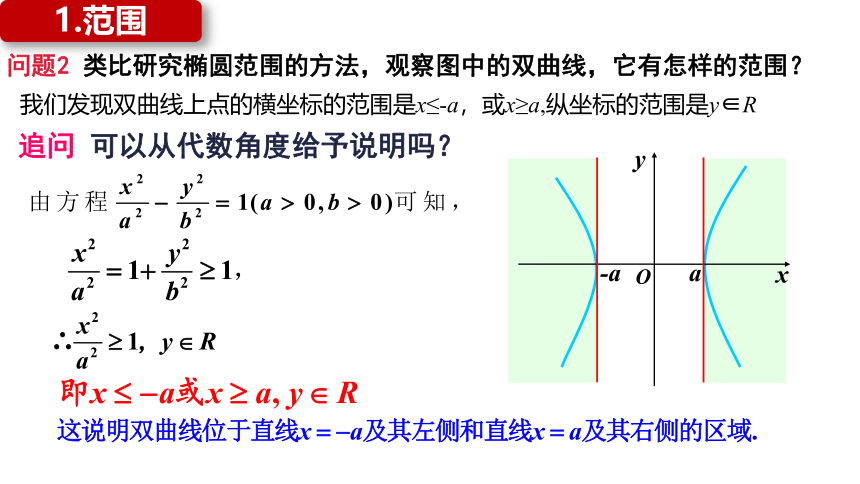
1.范围
我们发现双曲线上点的横坐标的范围是x≤-a,或x≥a,纵坐标的范围是y∈R
x
y
-a
a
O
问题2 类比研究椭圆范围的方法,观察图中的双曲线,它有怎样的范围?
追问 可以从代数角度给予说明吗?
x
y
-a
a
O
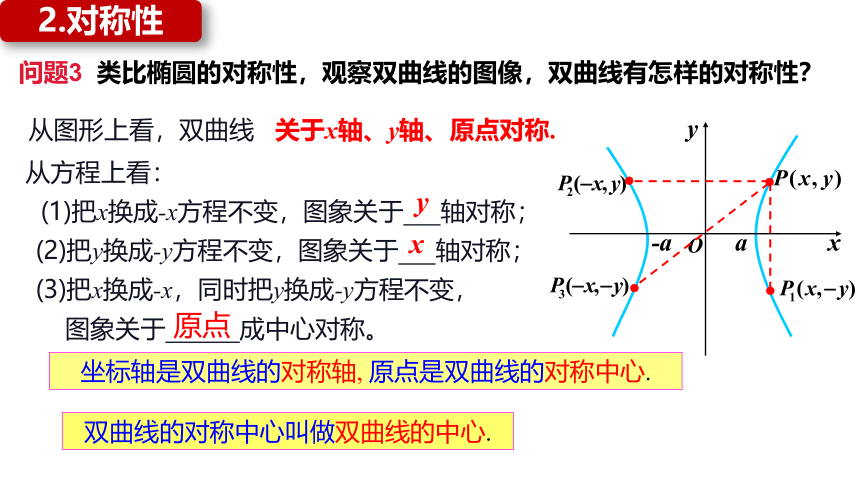
从图形上看,双曲线
从方程上看:
(1)把x换成-x方程不变,图象关于 轴对称;
(2)把y换成-y方程不变,图象关于 轴对称;
(3)把x换成-x,同时把y换成-y方程不变,
图象关于 成中心对称。
y
x
原点
坐标轴是双曲线的对称轴, 原点是双曲线的对称中心.
双曲线的对称中心叫做双曲线的中心.
2.对称性
关于x轴、y轴、原点对称.
问题3 类比椭圆的对称性,观察双曲线的图像,双曲线有怎样的对称性?
但我们也把 这两点画在y轴上(图3.2-8).
3.顶点
F1
F2
O
x
y
A1
说明它与x轴有两个交点, 坐标分别为
B1(0,-b),
B2(0,b)
A1(-a,0),
A2(a,0).
说明它与y轴没有交点,
线段A1A2, B1B2分别叫做双曲线的实轴和虚轴,它们的长分别等于2a,2b. a和b分别叫做椭圆的实半轴长和虚半轴长.
A2
B1
B2
图3.2-8
2a
2b
问题4 类比椭圆求顶点的方法,双曲线有多少个顶点
它们叫做双曲线的顶点.
4.离心率
与椭圆类似,双曲线的焦距与实轴长的比 称为双曲线的离心率.
∵c>a>0
∴e >1
问题5 双曲线的离心率与椭圆的离心率的范围有什么不同?
e的范围
4.离心率
追问1 椭圆的离心率刻画了椭圆的扁平程度,双曲线的离心率刻画双曲线的什么几何特征
发现:
e越大双曲线的开口就越“开阔”;
e越小,双曲线的开口就越“扁狭”
追问2:双曲线的离心率刻画了双曲线“张口”大小。可是这是为什么呢?这个悬念我们先暂时留一下,待到后面再讲。
5.渐近线
利用信息技术画出双曲线和两条直线.
问题5:观察图像并回答: 这两条直线有何特征?
x
y
B
1
B
2
O
F
2
F
1
A
2
A
1
5.渐近线
追问1 在双曲线的右支上取一点,测量点的横坐标以及它到直线的距离.沿曲线拖动点,观察与的大小关系,你发现了什么?
追问2:大家想不想知道其中的原因?
课后阅读课本128页的探究和发现
概念生成
一般地,双曲线()的两支向外延伸时,与两条直线逐渐接近,我们把这两条直线叫做双曲线的渐近线.实际上,双曲线与它的渐近线无限接近,但永远不相交.
追问1 如何记忆双曲线的渐近线方程?
在双曲线标准方程中,把“1”换成0即可!
追问2 渐近线对双曲线的开口有什么影响
渐近线与实轴的夹角越大,双曲线的开口也就越大
x
y
o
a
b
追问3 渐近线对画出双曲线简图有什么指导意义?
x
y
B
1
B
2
O
F
2
F
1
A
2
A
1
5.渐近线
这个矩形的对角线,也就是渐近线,可以比较快捷、较为准确地画出双曲线的图形。
画双曲线时,我们可以先画矩形框,然后画出双曲线的渐近线,最后再画双曲线。
当a=b时,这个矩形框是正方形,此时双曲线叫做等轴双曲线。
y
B2
A1
A2
B1
x
O
F2
F1
y
B2
A1
A2
B1
x
O
F2
F1
等轴双曲线
等轴双曲线的离心率e=
渐近线与离心率
问题7:离心率对双曲线图形形状的影响
x
y
B
1
B
2
O
F
2
F
1
A
2
A
1
新知探究二:—-焦点在轴时双曲线的性质
图象 范围 对称性 顶点 渐近线
离心率
或
或
关于坐标轴和原点都对称
性质
双曲线
关于坐标轴和原点都对称
例3 求双曲线9y2 – 16x2 =144的实半轴与虚半轴长,焦点坐标,离心率及渐近线方程, 并画出双曲线草图.
解:
3
-3
4
-4
x
y
O
F1(0,-5)
F2(0,5)
课堂例题
1. 求下列双曲线的实轴与虚轴的长, 顶点和焦点的坐标, 离心率, 渐近线方程.
解:
1. 求下列双曲线的实轴与虚轴的长, 顶点和焦点的坐标, 离心率, 渐近线方程.
解:
1. 求下列双曲线的实轴与虚轴的长, 顶点和焦点的坐标, 离心率, 渐近线方程.
解:
1. 求下列双曲线的实轴与虚轴的长, 顶点和焦点的坐标, 离心率, 渐近线方程.
解:
解:
解:
解:
解:
图象 范围 对称性 顶点 渐近线
离心率
或
或
关于坐标轴和原点都对称
总结双曲线的几何性质
性质
双曲线
关于坐标轴和原点都对称
课堂小结
第三章
圆锥曲线
3.2.2双曲线的简单几何性质
一
二
三
教学目标
了解并掌握双曲线的几何性质:对称性,范围,顶点,渐近线,离心率
理解离心率的大小对双曲线开口大小的影响
能利用双曲线的几何性质求双曲线的标准方程
学习目标
难点
重点
易错点
复习回顾
焦点在x轴的双曲线x2项系数为正.
焦点在y轴的双曲线y2项系数为正.
标准方程
相 同 点
焦点位置的判断
不 同 点
图 形
焦点坐标
定 义
a、b、c 的关系
c2-a2=b2
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹
x
F1
F2
y
O
M(x,y)
x
y
O
M(x,y)
F1
F2
新课导入
问题1类比对椭圆几何性质的研究,你认为应该研究双曲线
的哪些几何性质?如何研究这些性质?
范围、对称性、顶点、离心率
渐近线
下面,我们利用双曲线的标准方程
研究双曲线的几何性质.
新知探究
探究一:观察的形状,提炼出它的几何性质
观察双曲线 的形状, 你能从图上看出它的范围吗 它具有什么样的对称性 双曲线上哪些点比较特殊
1.范围
我们发现双曲线上点的横坐标的范围是x≤-a,或x≥a,纵坐标的范围是y∈R
x
y
-a
a
O
问题2 类比研究椭圆范围的方法,观察图中的双曲线,它有怎样的范围?
追问 可以从代数角度给予说明吗?
x
y
-a
a
O
从图形上看,双曲线
从方程上看:
(1)把x换成-x方程不变,图象关于 轴对称;
(2)把y换成-y方程不变,图象关于 轴对称;
(3)把x换成-x,同时把y换成-y方程不变,
图象关于 成中心对称。
y
x
原点
坐标轴是双曲线的对称轴, 原点是双曲线的对称中心.
双曲线的对称中心叫做双曲线的中心.
2.对称性
关于x轴、y轴、原点对称.
问题3 类比椭圆的对称性,观察双曲线的图像,双曲线有怎样的对称性?
但我们也把 这两点画在y轴上(图3.2-8).
3.顶点
F1
F2
O
x
y
A1
说明它与x轴有两个交点, 坐标分别为
B1(0,-b),
B2(0,b)
A1(-a,0),
A2(a,0).
说明它与y轴没有交点,
线段A1A2, B1B2分别叫做双曲线的实轴和虚轴,它们的长分别等于2a,2b. a和b分别叫做椭圆的实半轴长和虚半轴长.
A2
B1
B2
图3.2-8
2a
2b
问题4 类比椭圆求顶点的方法,双曲线有多少个顶点
它们叫做双曲线的顶点.
4.离心率
与椭圆类似,双曲线的焦距与实轴长的比 称为双曲线的离心率.
∵c>a>0
∴e >1
问题5 双曲线的离心率与椭圆的离心率的范围有什么不同?
e的范围
4.离心率
追问1 椭圆的离心率刻画了椭圆的扁平程度,双曲线的离心率刻画双曲线的什么几何特征
发现:
e越大双曲线的开口就越“开阔”;
e越小,双曲线的开口就越“扁狭”
追问2:双曲线的离心率刻画了双曲线“张口”大小。可是这是为什么呢?这个悬念我们先暂时留一下,待到后面再讲。
5.渐近线
利用信息技术画出双曲线和两条直线.
问题5:观察图像并回答: 这两条直线有何特征?
x
y
B
1
B
2
O
F
2
F
1
A
2
A
1
5.渐近线
追问1 在双曲线的右支上取一点,测量点的横坐标以及它到直线的距离.沿曲线拖动点,观察与的大小关系,你发现了什么?
追问2:大家想不想知道其中的原因?
课后阅读课本128页的探究和发现
概念生成
一般地,双曲线()的两支向外延伸时,与两条直线逐渐接近,我们把这两条直线叫做双曲线的渐近线.实际上,双曲线与它的渐近线无限接近,但永远不相交.
追问1 如何记忆双曲线的渐近线方程?
在双曲线标准方程中,把“1”换成0即可!
追问2 渐近线对双曲线的开口有什么影响
渐近线与实轴的夹角越大,双曲线的开口也就越大
x
y
o
a
b
追问3 渐近线对画出双曲线简图有什么指导意义?
x
y
B
1
B
2
O
F
2
F
1
A
2
A
1
5.渐近线
这个矩形的对角线,也就是渐近线,可以比较快捷、较为准确地画出双曲线的图形。
画双曲线时,我们可以先画矩形框,然后画出双曲线的渐近线,最后再画双曲线。
当a=b时,这个矩形框是正方形,此时双曲线叫做等轴双曲线。
y
B2
A1
A2
B1
x
O
F2
F1
y
B2
A1
A2
B1
x
O
F2
F1
等轴双曲线
等轴双曲线的离心率e=
渐近线与离心率
问题7:离心率对双曲线图形形状的影响
x
y
B
1
B
2
O
F
2
F
1
A
2
A
1
新知探究二:—-焦点在轴时双曲线的性质
图象 范围 对称性 顶点 渐近线
离心率
或
或
关于坐标轴和原点都对称
性质
双曲线
关于坐标轴和原点都对称
例3 求双曲线9y2 – 16x2 =144的实半轴与虚半轴长,焦点坐标,离心率及渐近线方程, 并画出双曲线草图.
解:
3
-3
4
-4
x
y
O
F1(0,-5)
F2(0,5)
课堂例题
1. 求下列双曲线的实轴与虚轴的长, 顶点和焦点的坐标, 离心率, 渐近线方程.
解:
1. 求下列双曲线的实轴与虚轴的长, 顶点和焦点的坐标, 离心率, 渐近线方程.
解:
1. 求下列双曲线的实轴与虚轴的长, 顶点和焦点的坐标, 离心率, 渐近线方程.
解:
1. 求下列双曲线的实轴与虚轴的长, 顶点和焦点的坐标, 离心率, 渐近线方程.
解:
解:
解:
解:
解:
图象 范围 对称性 顶点 渐近线
离心率
或
或
关于坐标轴和原点都对称
总结双曲线的几何性质
性质
双曲线
关于坐标轴和原点都对称
课堂小结
