青岛版六年级数学上册总复习《数与代数》教学课件(共34张PPT)
文档属性
| 名称 | 青岛版六年级数学上册总复习《数与代数》教学课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 00:00:00 | ||
图片预览






文档简介
(共34张PPT)
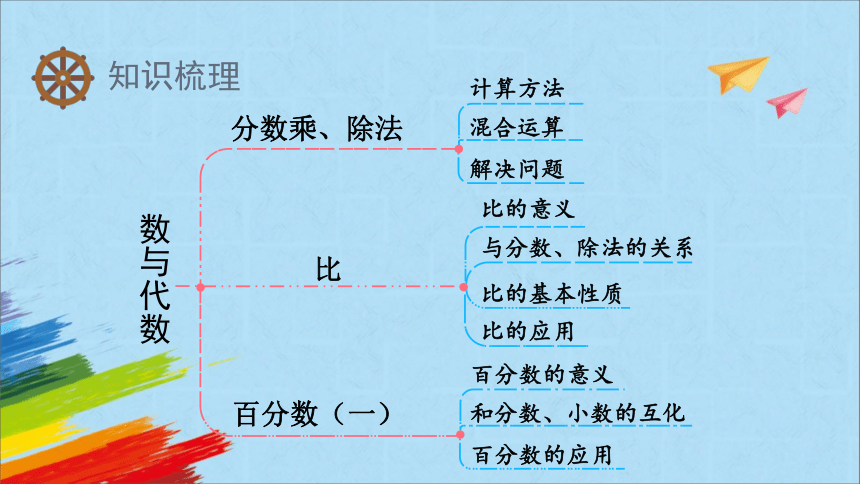
数与代数
数与代数
分数乘、除法
计算方法
混合运算
解决问题
比
比的意义
比的基本性质
比的应用
与分数、除法的关系
百分数(一)
百分数的意义
和分数、小数的互化
百分数的应用
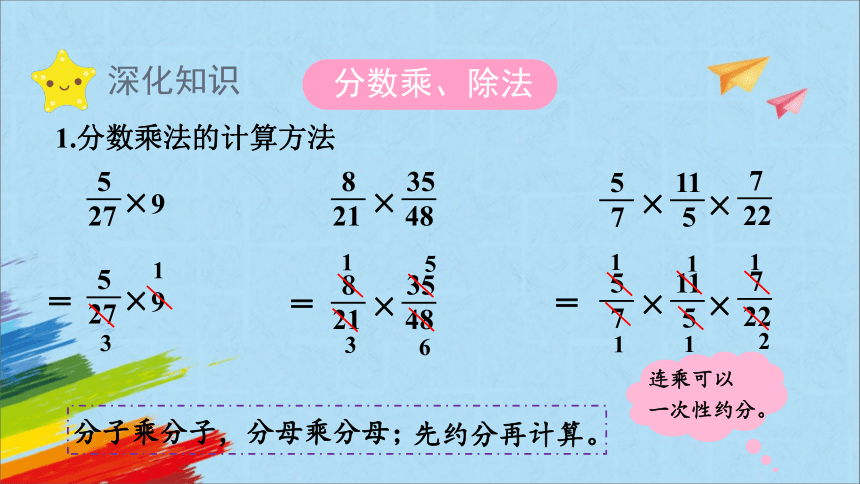
1.分数乘法的计算方法
27
5
×9
21
8
48
35
×
1
3
1
6
5
3
7
5
5
11
22
7
×
×
1
1
1
1
2
1
分子乘分子,分母乘分母;
连乘可以
一次性约分。
分数乘、除法
先约分再计算。
7
5
5
11
22
7
×
×
21
8
48
35
×
27
5
×9
=
=
=
2.分数除法的计算方法
5
12
÷4
8
3
÷
9
54
7
48
7
÷
5
12
4
1
×
=
3
1
9
3
8
×
=
1
3
54
7
7
48
×
=
1
1
9
8
除数变为倒数,转化为乘法计算。
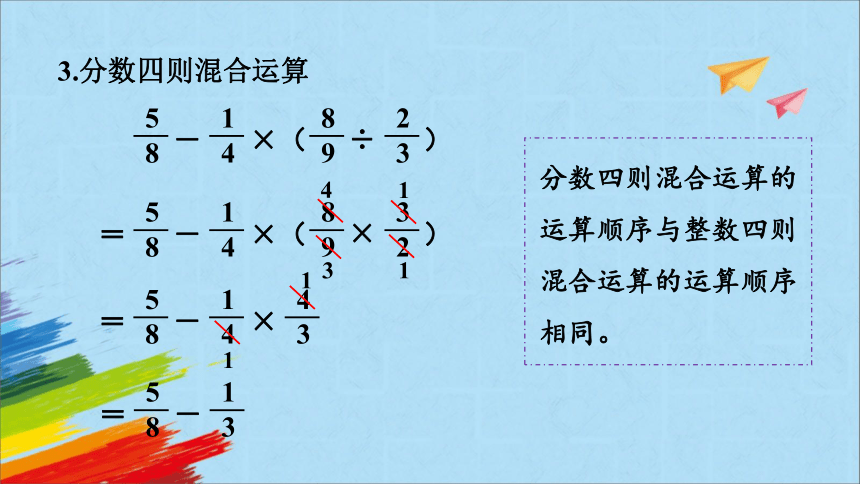
3.分数四则混合运算
8
5
-
4
1
×(
9
8
÷
3
2
)
8
5
-
4
1
×(
9
8
×
2
3
)
=
4
1
3
1
8
5
-
4
1
×
3
4
=
1
1
8
5
-
3
1
=
分数四则混合运算的运算顺序与整数四则混合运算的运算顺序相同。
16
9
17
×
16
9
=(16+1)
×
+
16
9
16
9
= 16×
1×
3.分数四则混合运算
×
4
7
8
1
×16
4
7
8
1
×(
×16)
=
2
1
4
7
×
2
=
1
2
1
1
整数的乘法交换律、乘法结合律、乘法分配律、除法的性质等对于分数同样适用。
9
5
4
5
5
4
÷
÷
( )
9
5
4
5
5
4
÷
×
=
1
1
1
1
9
5
1
÷
=
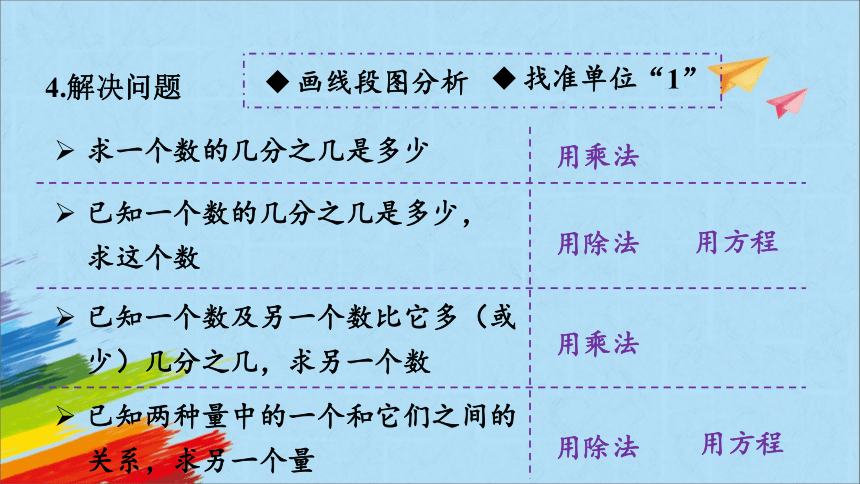
4.解决问题
求一个数的几分之几是多少
用乘法
已知一个数的几分之几是多少,求这个数
用除法
用方程
已知一个数及另一个数比它多(或少)几分之几,求另一个数
用乘法
已知两种量中的一个和它们之间的关系,求另一个量
用除法
用方程
画线段图分析
找准单位“1”
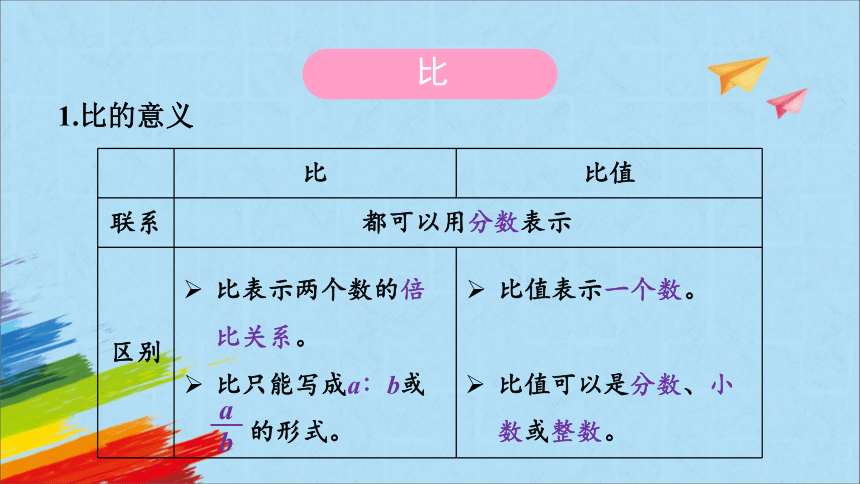
1.比的意义
比 比值
联系 区别
比值可以是分数、小数或整数。
都可以用分数表示
比表示两个数的倍比关系。
比值表示一个数。
比只能写成a∶b或
的形式。
a
b
比
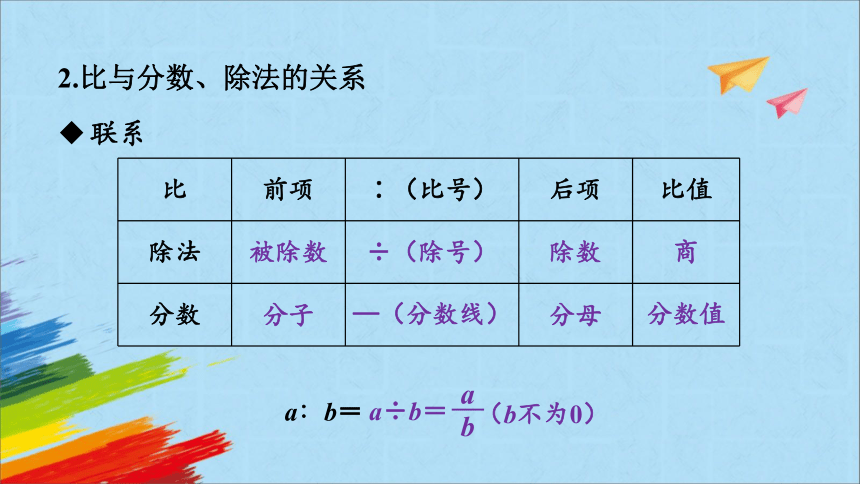
2.比与分数、除法的关系
联系
比 前项 ∶(比号) 后项 比值
除法
分数
被除数
÷(除号)
除数
商
分子
—(分数线)
分母
分数值
a∶b=
a÷b=
(b不为0)
a
b
2.比与分数、除法的关系
区别
比 除法 分数
意义
两个量(或数)的一种关系
一种运算
一种数
3.比的基本性质
8∶12 0.25∶0.35
=(8÷4) ∶(12÷4)
=(0.25×100)∶(0.35×100)
比的前项和后项同时乘或除以
相同的数(0除外),比值不变。
3.比的基本性质
8∶12 0.25∶0.35
=(8÷4) ∶(12÷4)
= 2∶ 3
=(0.25×100)∶(0.35×100)
= 5∶ 7
= 25∶ 35
化简比的依据是什么?
比的基本性质
4. 比的应用
周长:60cm
长和宽的比:3∶2
求长和宽各是多少?
方法一:
60÷2=30(cm)
长:30÷5×3=18(cm)
宽:30÷5×2=12(cm)
把各部分数看作份数关系
——按比分配
4. 比的应用
周长:60cm
长和宽的比:3∶2
求长和宽各是多少?
方法二:
60÷2=30(cm)
把各部分数看作总数的几分之几
——按比分配
1.百分数的意义
百分数 分数
联系 区别
表示两个数的比的关系,不能带单位名称。
都可以表示两个量之间的倍比关系
只表示两个数的比的关系,不能带单位名称。
表示一个具体的数,可以带单位名称。
百分数(一)
2.百分数和分数、小数的互化
百分数 20%
小数 0.85
分数
0.2
85%
75%
0.75
5
1
20
17
2.百分数和分数、小数的互化
小数
分数
先化成分母是10、100、1000……的分数,再约分
百分数
小数点向右移动两位,后面添上“%”
去掉“%” ,小数点向左移动两位
改写成分母是100的分数,再约分
化成小数
或分母是100的分数
分子除以分母
3.百分数的应用
求一个数是另一个数的百分之几
用除法
求百分率
学生的出勤率
结果一定是百分数。
如:
产品的合格率
合格人数
总数量
=
×100%
出勤人数
总人数
=
×100%
1.
2
×
=
6
÷
=
2.写出下面各数的倒数。
5
1
3
1
3.把下面各比化成最简单的整数比。
8∶42
0.25∶0.45
∶
=4∶21
=5∶9
=2∶1
4.判断对错,对的画“√”,错的画“×”。
(1)一个真分数的倒数一定比这个真分数大。
(2)一个数乘分数的积一定比原来的数小。
(3)一个数除以分数的商一定比原来的数大。
(4)大牛和小牛的头数比是4∶5,表示大牛比小牛少 。
( )
( )
( )
( )
√
×
×
√
5.下面各题怎样简便就怎样算。
5.下面各题怎样简便就怎样算。
5.下面各题怎样简便就怎样算。
6.地球上海洋面积是36000万平方千米,占地球总面积的
。地球总面积是多少万平方千米?
36000÷
=51000(万平方千米)
答:地球总面积是51000万平方千米。
7.三个同学跳绳。 小明跳了120个,小强跳的是小明跳的
,小亮跳的是小强跳的 。小亮跳了多少个?
答:小亮跳了50个。
120× ×
=50(个)
8.(1)五年级同学收集了165个易拉罐,六年级同学比五年级多收集了 。六年级收集了多少个易拉罐?
答:六年级收集了195个易拉罐。
165×(1+ )
=195(个)
8.(2)四年级比六年级少收集了 ,四年级收集了多少个易拉罐?
答:四年级收集了130个易拉罐。
195×(1- )
=130(个)
9.一列火车的速度是180千米/时。一辆小汽车的速度是这列火车的 ,是一架喷气式飞机的 。这架喷气式飞机的速度是多少?
答:这架喷气式飞机的速度是900千米/时。
180× ÷
=900(千米/时)
10.取小麦500g,烘干后,还有428g。计算出这种小麦的烘干率和含水率。
烘干率=
含水率=
11.在北纬70°以上的地方,一年连续约有2个月的时间没有夜晚,没有夜晚的时间占全年的_____ %。由于纬度比较高,瑞典首都斯德哥尔摩七月份的每天平均日照时间大约是一天的75%,有_____小时。
16.7
18
12.用84 cm长的铁丝围成一个三角形,这个三角形三条边长度的比是3∶4∶5。三条边分别是多少厘米?
答:三条边分别是21厘米、28 厘米、35 厘米。
千里之行,始于足下
数与代数
数与代数
分数乘、除法
计算方法
混合运算
解决问题
比
比的意义
比的基本性质
比的应用
与分数、除法的关系
百分数(一)
百分数的意义
和分数、小数的互化
百分数的应用
1.分数乘法的计算方法
27
5
×9
21
8
48
35
×
1
3
1
6
5
3
7
5
5
11
22
7
×
×
1
1
1
1
2
1
分子乘分子,分母乘分母;
连乘可以
一次性约分。
分数乘、除法
先约分再计算。
7
5
5
11
22
7
×
×
21
8
48
35
×
27
5
×9
=
=
=
2.分数除法的计算方法
5
12
÷4
8
3
÷
9
54
7
48
7
÷
5
12
4
1
×
=
3
1
9
3
8
×
=
1
3
54
7
7
48
×
=
1
1
9
8
除数变为倒数,转化为乘法计算。
3.分数四则混合运算
8
5
-
4
1
×(
9
8
÷
3
2
)
8
5
-
4
1
×(
9
8
×
2
3
)
=
4
1
3
1
8
5
-
4
1
×
3
4
=
1
1
8
5
-
3
1
=
分数四则混合运算的运算顺序与整数四则混合运算的运算顺序相同。
16
9
17
×
16
9
=(16+1)
×
+
16
9
16
9
= 16×
1×
3.分数四则混合运算
×
4
7
8
1
×16
4
7
8
1
×(
×16)
=
2
1
4
7
×
2
=
1
2
1
1
整数的乘法交换律、乘法结合律、乘法分配律、除法的性质等对于分数同样适用。
9
5
4
5
5
4
÷
÷
( )
9
5
4
5
5
4
÷
×
=
1
1
1
1
9
5
1
÷
=
4.解决问题
求一个数的几分之几是多少
用乘法
已知一个数的几分之几是多少,求这个数
用除法
用方程
已知一个数及另一个数比它多(或少)几分之几,求另一个数
用乘法
已知两种量中的一个和它们之间的关系,求另一个量
用除法
用方程
画线段图分析
找准单位“1”
1.比的意义
比 比值
联系 区别
比值可以是分数、小数或整数。
都可以用分数表示
比表示两个数的倍比关系。
比值表示一个数。
比只能写成a∶b或
的形式。
a
b
比
2.比与分数、除法的关系
联系
比 前项 ∶(比号) 后项 比值
除法
分数
被除数
÷(除号)
除数
商
分子
—(分数线)
分母
分数值
a∶b=
a÷b=
(b不为0)
a
b
2.比与分数、除法的关系
区别
比 除法 分数
意义
两个量(或数)的一种关系
一种运算
一种数
3.比的基本性质
8∶12 0.25∶0.35
=(8÷4) ∶(12÷4)
=(0.25×100)∶(0.35×100)
比的前项和后项同时乘或除以
相同的数(0除外),比值不变。
3.比的基本性质
8∶12 0.25∶0.35
=(8÷4) ∶(12÷4)
= 2∶ 3
=(0.25×100)∶(0.35×100)
= 5∶ 7
= 25∶ 35
化简比的依据是什么?
比的基本性质
4. 比的应用
周长:60cm
长和宽的比:3∶2
求长和宽各是多少?
方法一:
60÷2=30(cm)
长:30÷5×3=18(cm)
宽:30÷5×2=12(cm)
把各部分数看作份数关系
——按比分配
4. 比的应用
周长:60cm
长和宽的比:3∶2
求长和宽各是多少?
方法二:
60÷2=30(cm)
把各部分数看作总数的几分之几
——按比分配
1.百分数的意义
百分数 分数
联系 区别
表示两个数的比的关系,不能带单位名称。
都可以表示两个量之间的倍比关系
只表示两个数的比的关系,不能带单位名称。
表示一个具体的数,可以带单位名称。
百分数(一)
2.百分数和分数、小数的互化
百分数 20%
小数 0.85
分数
0.2
85%
75%
0.75
5
1
20
17
2.百分数和分数、小数的互化
小数
分数
先化成分母是10、100、1000……的分数,再约分
百分数
小数点向右移动两位,后面添上“%”
去掉“%” ,小数点向左移动两位
改写成分母是100的分数,再约分
化成小数
或分母是100的分数
分子除以分母
3.百分数的应用
求一个数是另一个数的百分之几
用除法
求百分率
学生的出勤率
结果一定是百分数。
如:
产品的合格率
合格人数
总数量
=
×100%
出勤人数
总人数
=
×100%
1.
2
×
=
6
÷
=
2.写出下面各数的倒数。
5
1
3
1
3.把下面各比化成最简单的整数比。
8∶42
0.25∶0.45
∶
=4∶21
=5∶9
=2∶1
4.判断对错,对的画“√”,错的画“×”。
(1)一个真分数的倒数一定比这个真分数大。
(2)一个数乘分数的积一定比原来的数小。
(3)一个数除以分数的商一定比原来的数大。
(4)大牛和小牛的头数比是4∶5,表示大牛比小牛少 。
( )
( )
( )
( )
√
×
×
√
5.下面各题怎样简便就怎样算。
5.下面各题怎样简便就怎样算。
5.下面各题怎样简便就怎样算。
6.地球上海洋面积是36000万平方千米,占地球总面积的
。地球总面积是多少万平方千米?
36000÷
=51000(万平方千米)
答:地球总面积是51000万平方千米。
7.三个同学跳绳。 小明跳了120个,小强跳的是小明跳的
,小亮跳的是小强跳的 。小亮跳了多少个?
答:小亮跳了50个。
120× ×
=50(个)
8.(1)五年级同学收集了165个易拉罐,六年级同学比五年级多收集了 。六年级收集了多少个易拉罐?
答:六年级收集了195个易拉罐。
165×(1+ )
=195(个)
8.(2)四年级比六年级少收集了 ,四年级收集了多少个易拉罐?
答:四年级收集了130个易拉罐。
195×(1- )
=130(个)
9.一列火车的速度是180千米/时。一辆小汽车的速度是这列火车的 ,是一架喷气式飞机的 。这架喷气式飞机的速度是多少?
答:这架喷气式飞机的速度是900千米/时。
180× ÷
=900(千米/时)
10.取小麦500g,烘干后,还有428g。计算出这种小麦的烘干率和含水率。
烘干率=
含水率=
11.在北纬70°以上的地方,一年连续约有2个月的时间没有夜晚,没有夜晚的时间占全年的_____ %。由于纬度比较高,瑞典首都斯德哥尔摩七月份的每天平均日照时间大约是一天的75%,有_____小时。
16.7
18
12.用84 cm长的铁丝围成一个三角形,这个三角形三条边长度的比是3∶4∶5。三条边分别是多少厘米?
答:三条边分别是21厘米、28 厘米、35 厘米。
千里之行,始于足下
