安徽省合肥市第三十八中学2022-2023学年九年级上学期期中考试数学试卷(含答案)
文档属性
| 名称 | 安徽省合肥市第三十八中学2022-2023学年九年级上学期期中考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 584.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 16:55:01 | ||
图片预览

文档简介
2022-2023学年度九年级第一学期期中考试数学试卷(38中)
温馨提示:
亲爱的同学,你拿到的试卷共八大题,满分150分,时间120分钟,希望你仔细审题,认答到困难时请不要轻易放弃,相信你一定会取得好成绩。
一、选择题(本大题共10小题,每小题4分,满分40分)
1.抛物线的顶点坐标是( )
A. B. C. D.
2.抛物线先向右平移3个单位长度,再向下平移2个单位长度得到的新抛物线解析式为( )
A. B. C. D.
3.下列长度的各组线段中,能组成比例线段的是( )
A.2,5,6,8 B.3,6,9,18 C.1,2,3,4 D.3,6,7,9
4.若二次函数的部分图象如图所示,则方程的解是( )
A. B.或-3 C., D.,
5.如果,,且b是a和c的比例中项,那么c等于( )
A. B. C. D.
6.点A、B是反比例函数的图象上关于原点O对称的任意两点,过点A作轴于点C,连接BC,则的面积为( )
A.1 B.2 C.3 D.4
7、对于反比例函数,下列结论:①图象分别在第二、四象限;②当时,y随x的增大而增大;③图象经过点;④若点,都在图象上,且,则,其中正确的是( )
A.①②③ B.②③④ C.①③④ D.①②④
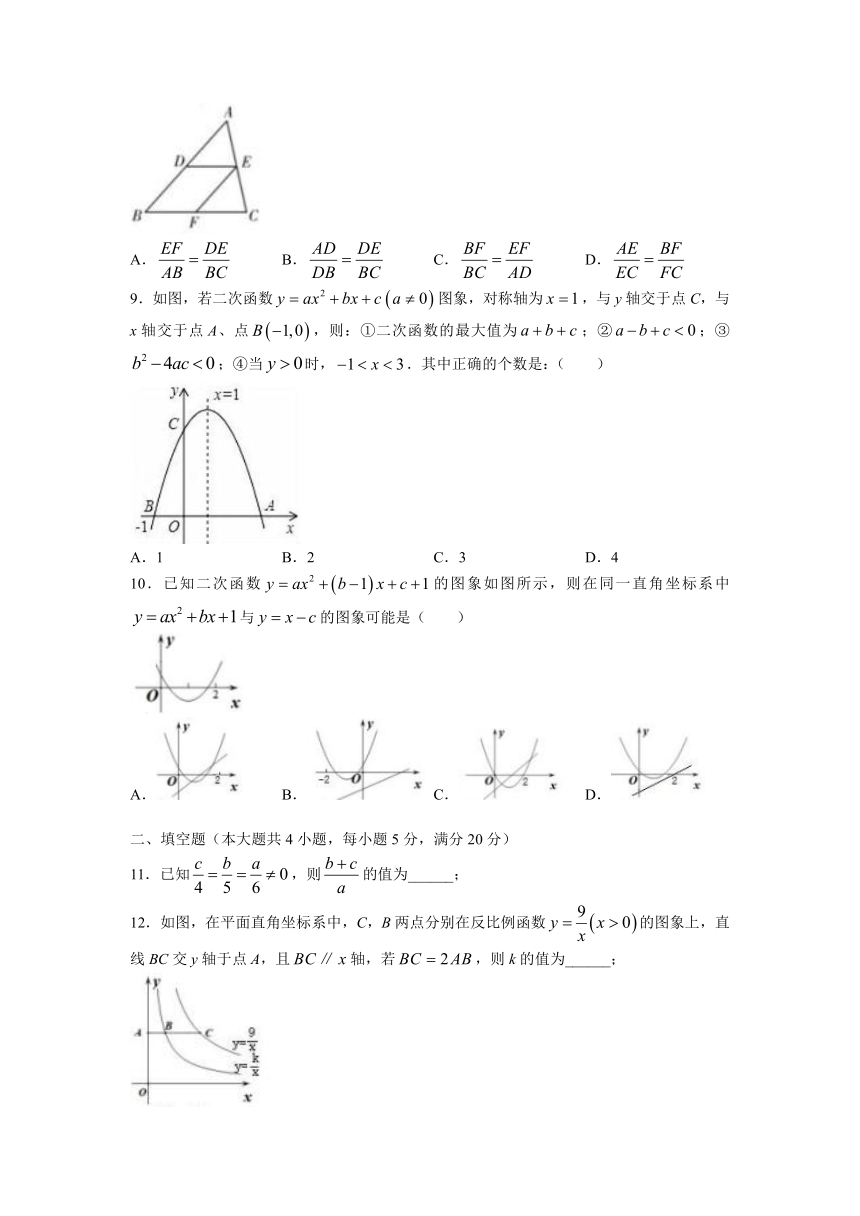
8.如图,中、若,,则下列比例式正确的是( )
A. B. C. D.
9.如图,若二次函数图象,对称轴为,与y轴交于点C,与x轴交于点A、点,则:①二次函数的最大值为;②;③;④当时,.其中正确的个数是:( )
A.1 B.2 C.3 D.4
10.已知二次函数的图象如图所示,则在同一直角坐标系中与的图象可能是( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知,则的值为______;
12.如图,在平面直角坐标系中,C,B两点分别在反比例函数的图象上,直线BC交y轴于点A,且轴,若,则k的值为______;
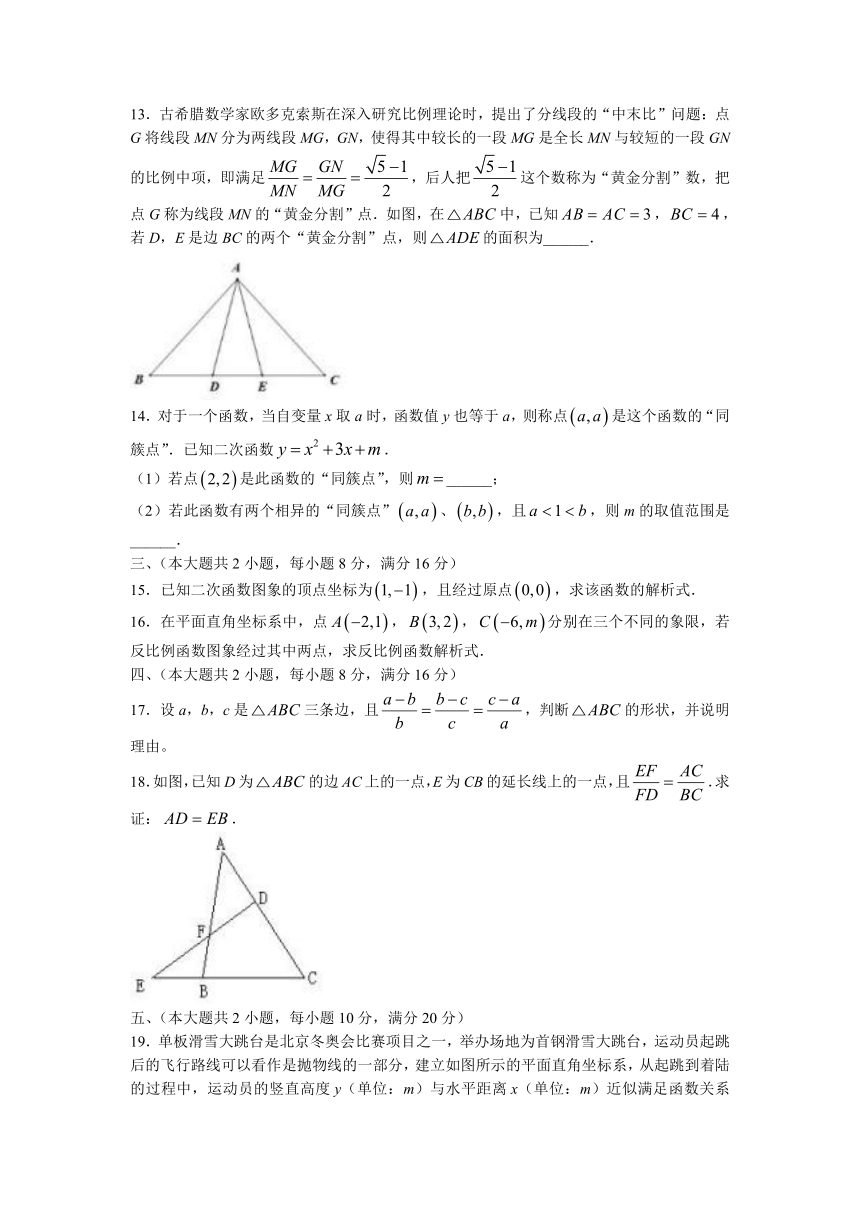
13.古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将线段MN分为两线段MG,GN,使得其中较长的一段MG是全长MN与较短的一段GN的比例中项,即满足,后人把这个数称为“黄金分割”数,把点G称为线段MN的“黄金分割”点.如图,在中,已知,,若D,E是边BC的两个“黄金分割”点,则的面积为______.
14.对于一个函数,当自变量x取a时,函数值y也等于a,则称点是这个函数的“同簇点”.已知二次函数.
(1)若点是此函数的“同簇点”,则______;
(2)若此函数有两个相异的“同簇点”、,且,则m的取值范围是______.
三、(本大题共2小题,每小题8分,满分16分)
15.已知二次函数图象的顶点坐标为,且经过原点,求该函数的解析式.
16.在平面直角坐标系中,点,,分别在三个不同的象限,若反比例函数图象经过其中两点,求反比例函数解析式.
四、(本大题共2小题,每小题8分,满分16分)
17.设a,b,c是三条边,且,判断的形状,并说明理由。
18.如图,已知D为的边AC上的一点,E为CB的延长线上的一点,且.求证:.
五、(本大题共2小题,每小题10分,满分20分)
19.单板滑雪大跳台是北京冬奥会比赛项目之一,举办场地为首钢滑雪大跳台,运动员起跳后的飞行路线可以看作是抛物线的一部分,建立如图所示的平面直角坐标系,从起跳到着陆的过程中,运动员的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系.
某运动员进行了两次训练.
(1)第一次训练时,该运动员的水平距离x与竖直高度y的几组数据如下:
水平距离x/m 0 2 5 8 11 14
竖直高度y/m 20.00 21.40 22.75 23.20 22.75 21.40
根据上述数据,直接写出满足的函数关系;
(2)第二训练时该运动员竖直高度y与水平距离x近似满足函数关系,记该运动员第一次训练的着陆点的水平距离为,第二次训练的着陆点的水平距离为,试比较与的大小,并说明理由.
20.如图直线与双曲线相交于A、B两点,与y轴交于点C,轴,垂足为D,已知.
(1)求此双曲线的函数表达式;
(2)求点A,B的坐标;
(3)直接写出不等式的解集.
六、(本题满分12分)
21.如图,抛物线与x轴交于A,B两点,与y轴交于点C,已知点B的坐标为,点C的坐标为.
(1)求抛物线的表达式:
(2)点P为直线BC上方抛物线上的一个动点,当的面积最大时,求点P的坐标.
七、(本题满分12分)
22.大学生小张利用暑假50天在一超市勤工俭学,被安排销售一款成本为40元/件的新型商品,此类新型商品在第x天的销售量p件与销售的天数x的关系如下表:
x(天) 1 2 3 … 50
p(件) 118 116 114 … 20
销售单价q(元/件)与x满足:当时;当时.
(1)请分析表格中销售量p与x的关系,直接写出销售量p与x的函数关系;
(2)求该超市销售该新商品第x天获得的利润y元关于x的函数关系式;
(3)这50天中,该超市第几天获得利润最大 最大利润为多少?
八、(本题满分14分)
23.图(1)是房屋窗户上方的墙上安装的抛物线形遮阳棚,其大致轮廓可以看作如图(2)所示的抛物线AB.且抛物线AB的解析式为,已知米,米.
(1)求出抛物线AB的解析式(不需要写出x的取值范围)。
(2)为了加强遮阳棚的稳固性,现在遮阳棚两侧加装支架,如图(2),,,,,都平行于y轴,平行于x轴,且,设一侧支架的总长,点的坐标为.
①试求出l与m之间的函数关系式;
②现有3米长的材料,按以上设计要求,能否完成一侧支架的安装?
答案:1~10BCBCCBADBA
11. 12.3 13.
14.(1)-8(2)(提示:,在图象上,联立,得,,即,令,则其图象与x轴有两个交点,,
∵,∴当时,,∴,∴).
15.
16.时经过B、C两,;时,不存在.
17.是等边三角形.理由如下:设,则,,,∵a、b、c是的边,∴,∴,∴,∴是等边三角形.
18.过点D作交BC于M,∴,,又,∴,∴.
19.(1),
(2)当时,由得,解得(舍去),,∴;由得,解得(舍去),,∴,,∴.
20.(1),(2)设直线BC的解析式为,代入B、C坐标得,解得,,∴,过点P作轴于点H,交BC于点Q,设,则,∴,
∴,
∵,∴时,最大,为.此时.
22.(1);(2),(3)当时,,∵-,∴当时,y有最大值3200(元);当时,,∵,∴随x增大而减小,∴当时,有最大值3150(元).∵,∴这50天中该超市第20天时获得的利润最大,最大利润为3200元.
23.(1);
(2),,
,,
,∴;
(3),∴当时,l取得最大值2.775,
∵,∴3米长的材料按以上设计可以完成支架的安装.
温馨提示:
亲爱的同学,你拿到的试卷共八大题,满分150分,时间120分钟,希望你仔细审题,认答到困难时请不要轻易放弃,相信你一定会取得好成绩。
一、选择题(本大题共10小题,每小题4分,满分40分)
1.抛物线的顶点坐标是( )
A. B. C. D.
2.抛物线先向右平移3个单位长度,再向下平移2个单位长度得到的新抛物线解析式为( )
A. B. C. D.
3.下列长度的各组线段中,能组成比例线段的是( )
A.2,5,6,8 B.3,6,9,18 C.1,2,3,4 D.3,6,7,9
4.若二次函数的部分图象如图所示,则方程的解是( )
A. B.或-3 C., D.,
5.如果,,且b是a和c的比例中项,那么c等于( )
A. B. C. D.
6.点A、B是反比例函数的图象上关于原点O对称的任意两点,过点A作轴于点C,连接BC,则的面积为( )
A.1 B.2 C.3 D.4
7、对于反比例函数,下列结论:①图象分别在第二、四象限;②当时,y随x的增大而增大;③图象经过点;④若点,都在图象上,且,则,其中正确的是( )
A.①②③ B.②③④ C.①③④ D.①②④
8.如图,中、若,,则下列比例式正确的是( )
A. B. C. D.
9.如图,若二次函数图象,对称轴为,与y轴交于点C,与x轴交于点A、点,则:①二次函数的最大值为;②;③;④当时,.其中正确的个数是:( )
A.1 B.2 C.3 D.4
10.已知二次函数的图象如图所示,则在同一直角坐标系中与的图象可能是( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知,则的值为______;
12.如图,在平面直角坐标系中,C,B两点分别在反比例函数的图象上,直线BC交y轴于点A,且轴,若,则k的值为______;
13.古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将线段MN分为两线段MG,GN,使得其中较长的一段MG是全长MN与较短的一段GN的比例中项,即满足,后人把这个数称为“黄金分割”数,把点G称为线段MN的“黄金分割”点.如图,在中,已知,,若D,E是边BC的两个“黄金分割”点,则的面积为______.
14.对于一个函数,当自变量x取a时,函数值y也等于a,则称点是这个函数的“同簇点”.已知二次函数.
(1)若点是此函数的“同簇点”,则______;
(2)若此函数有两个相异的“同簇点”、,且,则m的取值范围是______.
三、(本大题共2小题,每小题8分,满分16分)
15.已知二次函数图象的顶点坐标为,且经过原点,求该函数的解析式.
16.在平面直角坐标系中,点,,分别在三个不同的象限,若反比例函数图象经过其中两点,求反比例函数解析式.
四、(本大题共2小题,每小题8分,满分16分)
17.设a,b,c是三条边,且,判断的形状,并说明理由。
18.如图,已知D为的边AC上的一点,E为CB的延长线上的一点,且.求证:.
五、(本大题共2小题,每小题10分,满分20分)
19.单板滑雪大跳台是北京冬奥会比赛项目之一,举办场地为首钢滑雪大跳台,运动员起跳后的飞行路线可以看作是抛物线的一部分,建立如图所示的平面直角坐标系,从起跳到着陆的过程中,运动员的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系.
某运动员进行了两次训练.
(1)第一次训练时,该运动员的水平距离x与竖直高度y的几组数据如下:
水平距离x/m 0 2 5 8 11 14
竖直高度y/m 20.00 21.40 22.75 23.20 22.75 21.40
根据上述数据,直接写出满足的函数关系;
(2)第二训练时该运动员竖直高度y与水平距离x近似满足函数关系,记该运动员第一次训练的着陆点的水平距离为,第二次训练的着陆点的水平距离为,试比较与的大小,并说明理由.
20.如图直线与双曲线相交于A、B两点,与y轴交于点C,轴,垂足为D,已知.
(1)求此双曲线的函数表达式;
(2)求点A,B的坐标;
(3)直接写出不等式的解集.
六、(本题满分12分)
21.如图,抛物线与x轴交于A,B两点,与y轴交于点C,已知点B的坐标为,点C的坐标为.
(1)求抛物线的表达式:
(2)点P为直线BC上方抛物线上的一个动点,当的面积最大时,求点P的坐标.
七、(本题满分12分)
22.大学生小张利用暑假50天在一超市勤工俭学,被安排销售一款成本为40元/件的新型商品,此类新型商品在第x天的销售量p件与销售的天数x的关系如下表:
x(天) 1 2 3 … 50
p(件) 118 116 114 … 20
销售单价q(元/件)与x满足:当时;当时.
(1)请分析表格中销售量p与x的关系,直接写出销售量p与x的函数关系;
(2)求该超市销售该新商品第x天获得的利润y元关于x的函数关系式;
(3)这50天中,该超市第几天获得利润最大 最大利润为多少?
八、(本题满分14分)
23.图(1)是房屋窗户上方的墙上安装的抛物线形遮阳棚,其大致轮廓可以看作如图(2)所示的抛物线AB.且抛物线AB的解析式为,已知米,米.
(1)求出抛物线AB的解析式(不需要写出x的取值范围)。
(2)为了加强遮阳棚的稳固性,现在遮阳棚两侧加装支架,如图(2),,,,,都平行于y轴,平行于x轴,且,设一侧支架的总长,点的坐标为.
①试求出l与m之间的函数关系式;
②现有3米长的材料,按以上设计要求,能否完成一侧支架的安装?
答案:1~10BCBCCBADBA
11. 12.3 13.
14.(1)-8(2)(提示:,在图象上,联立,得,,即,令,则其图象与x轴有两个交点,,
∵,∴当时,,∴,∴).
15.
16.时经过B、C两,;时,不存在.
17.是等边三角形.理由如下:设,则,,,∵a、b、c是的边,∴,∴,∴,∴是等边三角形.
18.过点D作交BC于M,∴,,又,∴,∴.
19.(1),
(2)当时,由得,解得(舍去),,∴;由得,解得(舍去),,∴,,∴.
20.(1),(2)设直线BC的解析式为,代入B、C坐标得,解得,,∴,过点P作轴于点H,交BC于点Q,设,则,∴,
∴,
∵,∴时,最大,为.此时.
22.(1);(2),(3)当时,,∵-,∴当时,y有最大值3200(元);当时,,∵,∴随x增大而减小,∴当时,有最大值3150(元).∵,∴这50天中该超市第20天时获得的利润最大,最大利润为3200元.
23.(1);
(2),,
,,
,∴;
(3),∴当时,l取得最大值2.775,
∵,∴3米长的材料按以上设计可以完成支架的安装.
同课章节目录
