人教A版(2019)数学必修第一册5_5_1_2两角和与差的正切公式课件(共28张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第一册5_5_1_2两角和与差的正切公式课件(共28张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
5.5.1.2 两角和与差的正切公式
高一
必修一
本节目标
1.能利用两角和与差的正弦、余弦公式推导出两角和与差的正切公式.
2.能利用两角和与差的正切公式进行化简、求值、证明.
任务一:知识预习
课前预习
1. tan α,sin α,cos α的关系怎样?利用该关系式及两角和的正、余弦公式,能把tan(α+β)用tan α,tan β表示吗?
2. 怎样用tan α,tan β表示tan(α-β)吗?
预习课本P217~220,思考并完成以下问题
任务二:简单题型通关
课前预习
B
任务二:简单题型通关
课前预习
A
任务二:简单题型通关
课前预习
3.A,B,C是△ABC的三个内角,且tan A,tan B是方程3x2-5x+1=0的两个实数根,则△ABC是( )
A.钝角三角形 B.锐角三角形
C.直角三角形 D.无法确定
A
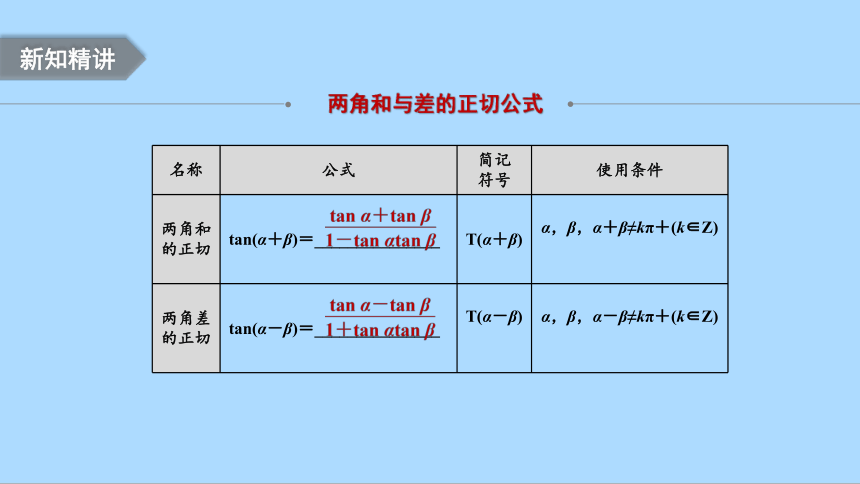
名称 公式 简记 符号 使用条件
两角和 的正切 tan(α+β)=_______________ T(α+β) α,β,α+β≠kπ+(k∈Z)
两角差 的正切 tan(α-β)=_______________ T(α-β) α,β,α-β≠kπ+(k∈Z)
新知精讲
两角和与差的正切公式
新知精讲
化简疑难
新知精讲
化简疑难
题型探究
题型一
化简求值问题
题型探究
题型一
化简求值问题
归纳总结
利用公式T(α±β)化简求值的两点说明
(1)分析式子结构,正确选用公式形式:
T(α±β)是三角函数公式中应用灵活程度较高的公式之一,因此在应用时先从所化简(求值)式子的结构出发,确定是正用、逆用还是变形用,并注意整体代换.
(2)化简求值中要注意“特殊值”的代换和应用:
当所要化简(求值)的式子中出现特殊的数值“1”、“”时,要考虑用这些特殊值所对应的特殊角的正切值去代换,如“1=tan”、“=tan”,这样可以构造出利用公式的条件,从而可以进行化简和求值.
活学活用
法一
活学活用
法一
法二
活学活用
题型探究
题型二
条件求值问题
归纳总结
(1)式子的变换:分析已知式子的结构特点,结合两角和与差的三角函数公式,通过变形,建立与待求式间的联系实现求值.
(2)角的变换:首先从已知角间的关系入手,分析已知角和待求角间的关系,如用α=β-(β-α)、2α=(α+β)+(α-β)等关系,把待求的三角函数与已知角的三角函数巧妙地建立等量关系,从而求值.
给值求值问题的两种变换
解题策略
活学活用
题型探究
题型三
给值求角问题
法一
题型探究
题型三
给值求角问题
法二
归纳总结
解决给值求角问题的步骤
解决给值求角问题,以下两个步骤缺一不可:
(1)根据题设条件求角的某一三角函数值;
(2)讨论角的范围,必要时还需根据已知三角函数值缩小角的范围,从而确定角的大小.
方法总结
活学活用
D
达标检测
达标检测
达标检测
3.已知tan α+tan β=2,tan(α+β)=4,则tan α·tan β=________.
达标检测
达标检测
本课小结
5.5.1.2 两角和与差的正切公式
高一
必修一
本节目标
1.能利用两角和与差的正弦、余弦公式推导出两角和与差的正切公式.
2.能利用两角和与差的正切公式进行化简、求值、证明.
任务一:知识预习
课前预习
1. tan α,sin α,cos α的关系怎样?利用该关系式及两角和的正、余弦公式,能把tan(α+β)用tan α,tan β表示吗?
2. 怎样用tan α,tan β表示tan(α-β)吗?
预习课本P217~220,思考并完成以下问题
任务二:简单题型通关
课前预习
B
任务二:简单题型通关
课前预习
A
任务二:简单题型通关
课前预习
3.A,B,C是△ABC的三个内角,且tan A,tan B是方程3x2-5x+1=0的两个实数根,则△ABC是( )
A.钝角三角形 B.锐角三角形
C.直角三角形 D.无法确定
A
名称 公式 简记 符号 使用条件
两角和 的正切 tan(α+β)=_______________ T(α+β) α,β,α+β≠kπ+(k∈Z)
两角差 的正切 tan(α-β)=_______________ T(α-β) α,β,α-β≠kπ+(k∈Z)
新知精讲
两角和与差的正切公式
新知精讲
化简疑难
新知精讲
化简疑难
题型探究
题型一
化简求值问题
题型探究
题型一
化简求值问题
归纳总结
利用公式T(α±β)化简求值的两点说明
(1)分析式子结构,正确选用公式形式:
T(α±β)是三角函数公式中应用灵活程度较高的公式之一,因此在应用时先从所化简(求值)式子的结构出发,确定是正用、逆用还是变形用,并注意整体代换.
(2)化简求值中要注意“特殊值”的代换和应用:
当所要化简(求值)的式子中出现特殊的数值“1”、“”时,要考虑用这些特殊值所对应的特殊角的正切值去代换,如“1=tan”、“=tan”,这样可以构造出利用公式的条件,从而可以进行化简和求值.
活学活用
法一
活学活用
法一
法二
活学活用
题型探究
题型二
条件求值问题
归纳总结
(1)式子的变换:分析已知式子的结构特点,结合两角和与差的三角函数公式,通过变形,建立与待求式间的联系实现求值.
(2)角的变换:首先从已知角间的关系入手,分析已知角和待求角间的关系,如用α=β-(β-α)、2α=(α+β)+(α-β)等关系,把待求的三角函数与已知角的三角函数巧妙地建立等量关系,从而求值.
给值求值问题的两种变换
解题策略
活学活用
题型探究
题型三
给值求角问题
法一
题型探究
题型三
给值求角问题
法二
归纳总结
解决给值求角问题的步骤
解决给值求角问题,以下两个步骤缺一不可:
(1)根据题设条件求角的某一三角函数值;
(2)讨论角的范围,必要时还需根据已知三角函数值缩小角的范围,从而确定角的大小.
方法总结
活学活用
D
达标检测
达标检测
达标检测
3.已知tan α+tan β=2,tan(α+β)=4,则tan α·tan β=________.
达标检测
达标检测
本课小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
