人教A版(2019)数学必修第一册5_5_1_3二倍角的正弦、余弦、正切公式课件(共23张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第一册5_5_1_3二倍角的正弦、余弦、正切公式课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 20:35:12 | ||
图片预览




文档简介
(共23张PPT)
5.5.1.3 二倍角的正弦、余弦、正切公式
高一
必修一
本节目标
1.理解二倍角的正弦、余弦、正切公式及其推导过程.
2.能够灵活运用二倍角的正弦、余弦、正切公式进行化简、求值、证明.
任务一:知识预习
课前预习
预习课本P220~223,思考并完成以下问题
(1)二倍角的正弦、余弦、正切公式是什么?公式如何推导?
(2)S2α,C2α,T2α中角α的取值范围分别是什么?
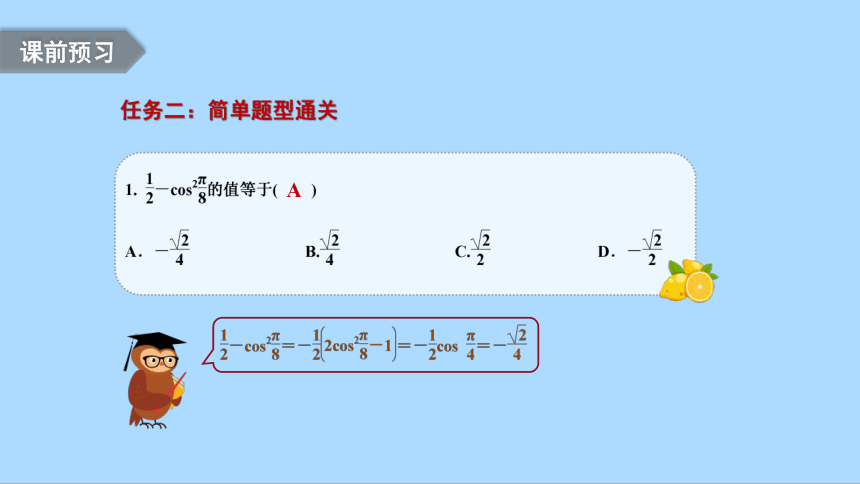
任务二:简单题型通关
课前预习
A
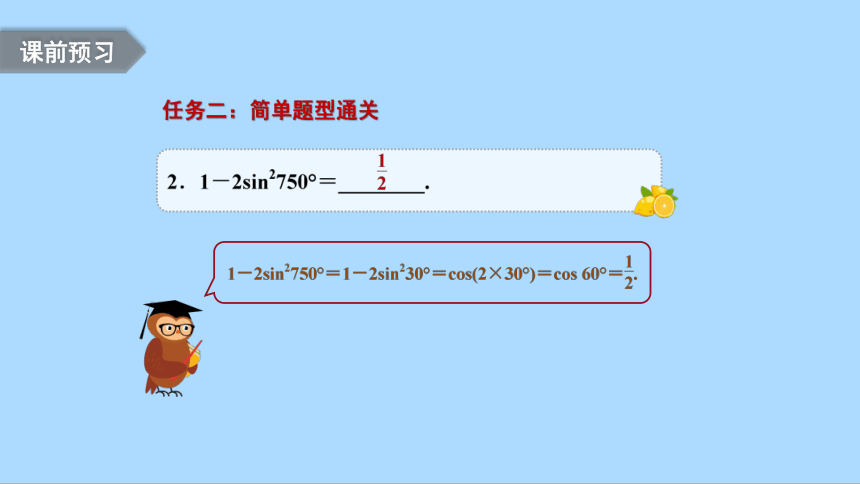
任务二:简单题型通关
课前预习
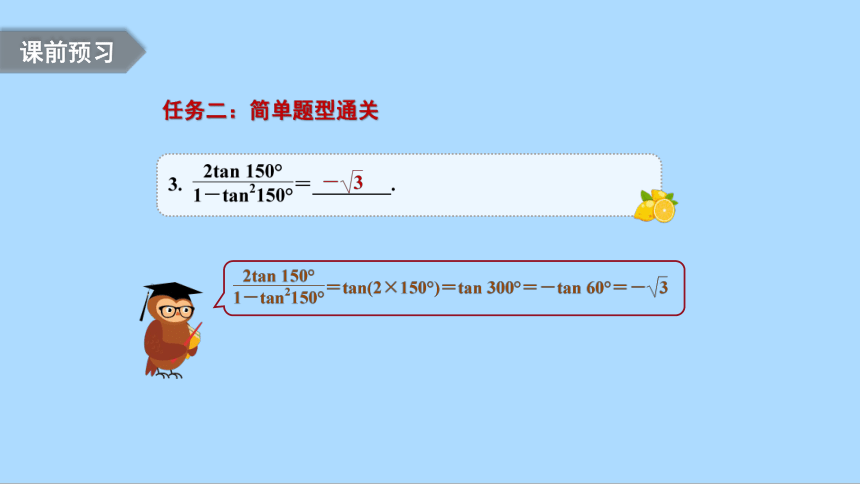
任务二:简单题型通关
课前预习
新知精讲
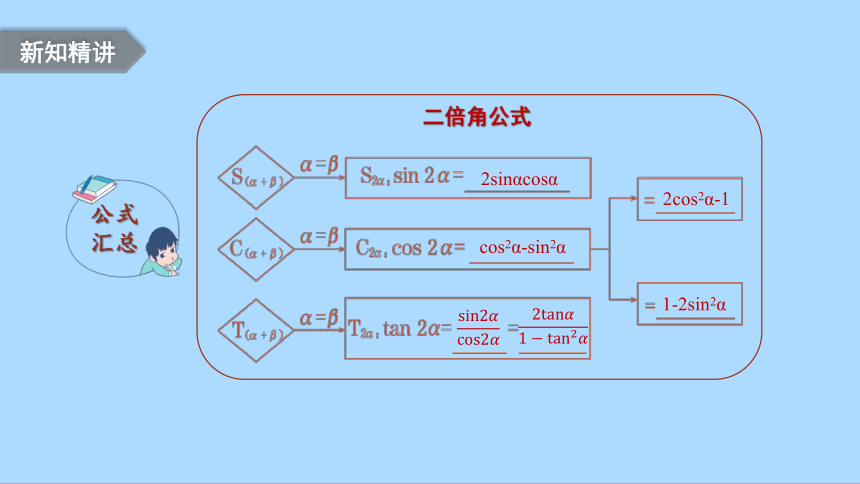
二倍角公式
2sinαcosα
cos2α-sin2α
2cos2α-1
1-2sin2α
公式汇总
新知精讲
拓展延伸
题型探究
题型一
给角求值问题
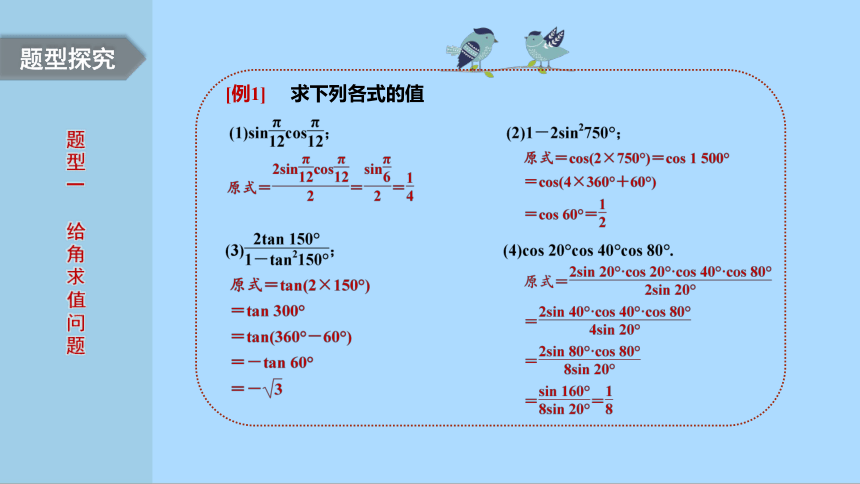
[例1] 求下列各式的值
归纳总结
此类题型(1)(2)(3)小题直接利用公式或逆用公式较为简单.而(4)小题通过观察角度的关系,发现其特征(二倍角形式),逆用正弦二倍角公式,使得问题中可连用正弦二倍角公式,所以在解题过程中要注意观察式子的结构特点及角之间是否存在特殊的倍数关系,灵活运用公式及其变形,从而使问题迎刃而解.
方法总结
活学活用
1.求下列各式的值.
题型探究
题型二 化简问题
归纳总结
化简三角函数式的常用方法:
①切化弦;
②异名化同名;
③异角化同角;
④高次降低次.
解题方法
归纳总结
化简三角函数式的常用技巧
①特殊角的三角函数与特殊值的互化;
②对于分式形式,应分别对分子、分母进行变形处理,有公因式的提取公因式后进行约分;
③对于二次根式,注意倍角公式的逆用;
④利用角与角之间的隐含关系,如互余、互补等;
⑤利用“1”的恒等变形,如tan 45°=1,sin2α+cos2α=1等.
解题技巧
活学活用
题型探究
题型三 给值求值问题
题型探究
一题多变
题型探究
一题多变
归纳总结
解决给值求值问题的方法
给值求值问题,注意寻找已知式与未知式之间的联系,有两个观察方向:
(1)有方向地将已知式或未知式化简,使关系明朗化;
(2)寻找角之间的关系,看是否适合相关公式的使用,注意常见角的变换和角之间的二倍关系.
达标检测
D
达标检测
B
达标检测
本课小结
1.二倍角的正弦、余弦、正切公式是什么?
2. S2α,C2α,T2α中角α的取值范围分别是什么?
3. 化简三角函数式的常用方法有哪些?
5.5.1.3 二倍角的正弦、余弦、正切公式
高一
必修一
本节目标
1.理解二倍角的正弦、余弦、正切公式及其推导过程.
2.能够灵活运用二倍角的正弦、余弦、正切公式进行化简、求值、证明.
任务一:知识预习
课前预习
预习课本P220~223,思考并完成以下问题
(1)二倍角的正弦、余弦、正切公式是什么?公式如何推导?
(2)S2α,C2α,T2α中角α的取值范围分别是什么?
任务二:简单题型通关
课前预习
A
任务二:简单题型通关
课前预习
任务二:简单题型通关
课前预习
新知精讲
二倍角公式
2sinαcosα
cos2α-sin2α
2cos2α-1
1-2sin2α
公式汇总
新知精讲
拓展延伸
题型探究
题型一
给角求值问题
[例1] 求下列各式的值
归纳总结
此类题型(1)(2)(3)小题直接利用公式或逆用公式较为简单.而(4)小题通过观察角度的关系,发现其特征(二倍角形式),逆用正弦二倍角公式,使得问题中可连用正弦二倍角公式,所以在解题过程中要注意观察式子的结构特点及角之间是否存在特殊的倍数关系,灵活运用公式及其变形,从而使问题迎刃而解.
方法总结
活学活用
1.求下列各式的值.
题型探究
题型二 化简问题
归纳总结
化简三角函数式的常用方法:
①切化弦;
②异名化同名;
③异角化同角;
④高次降低次.
解题方法
归纳总结
化简三角函数式的常用技巧
①特殊角的三角函数与特殊值的互化;
②对于分式形式,应分别对分子、分母进行变形处理,有公因式的提取公因式后进行约分;
③对于二次根式,注意倍角公式的逆用;
④利用角与角之间的隐含关系,如互余、互补等;
⑤利用“1”的恒等变形,如tan 45°=1,sin2α+cos2α=1等.
解题技巧
活学活用
题型探究
题型三 给值求值问题
题型探究
一题多变
题型探究
一题多变
归纳总结
解决给值求值问题的方法
给值求值问题,注意寻找已知式与未知式之间的联系,有两个观察方向:
(1)有方向地将已知式或未知式化简,使关系明朗化;
(2)寻找角之间的关系,看是否适合相关公式的使用,注意常见角的变换和角之间的二倍关系.
达标检测
D
达标检测
B
达标检测
本课小结
1.二倍角的正弦、余弦、正切公式是什么?
2. S2α,C2α,T2α中角α的取值范围分别是什么?
3. 化简三角函数式的常用方法有哪些?
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
