27.2.1 相似三角形的判定
文档属性
| 名称 | 27.2.1 相似三角形的判定 |  | |
| 格式 | zip | ||
| 文件大小 | 781.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-23 15:52:12 | ||
图片预览


文档简介
课件25张PPT。27.2.1相似三角形的判定(2)三条平行线截两条直线,所得的对应线段的比相等.平行线分线段成比例定理:∵ DE∥BC
∵ DE∥BC
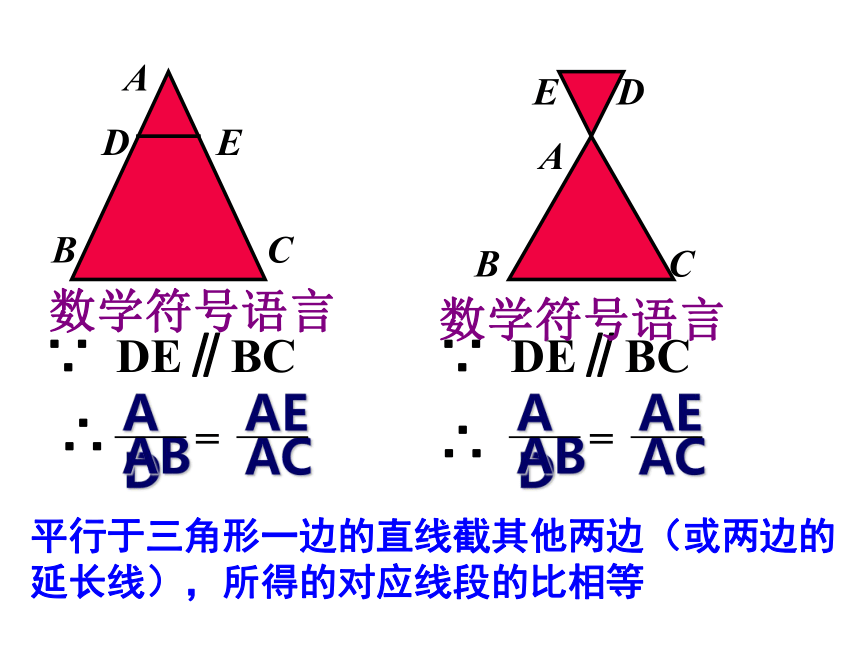
数学符号语言数学符号语言平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等 平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.在△ADE与△ABC中,
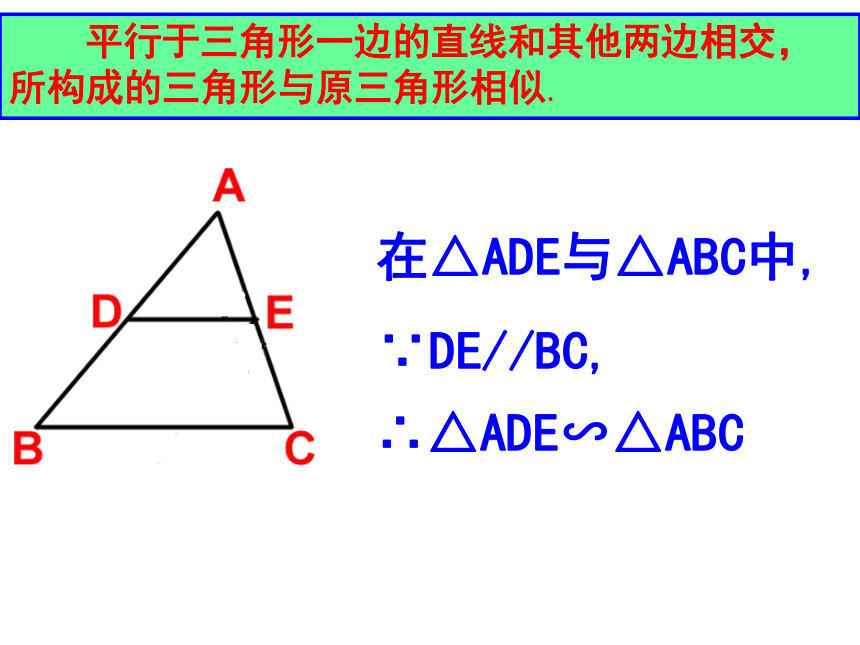
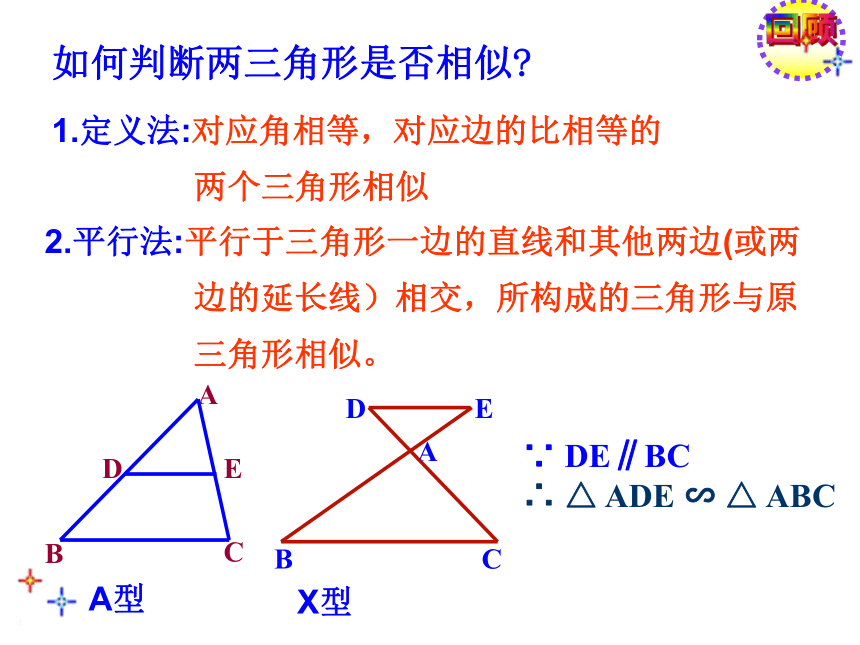
∵DE//BC,∴△ADE∽△ABC1.定义法:对应角相等,对应边的比相等的
两个三角形相似回顾如何判断两三角形是否相似? ∵ DE∥BC
∴ △ ADE ∽ △ ABC 2.平行法:平行于三角形一边的直线和其他两边(或两
边的延长线)相交,所构成的三角形与原
三角形相似。A型X型猜想? 有没有其他简单的办法判断两个三角形相似呢? 三角形全等有哪几种简单的判
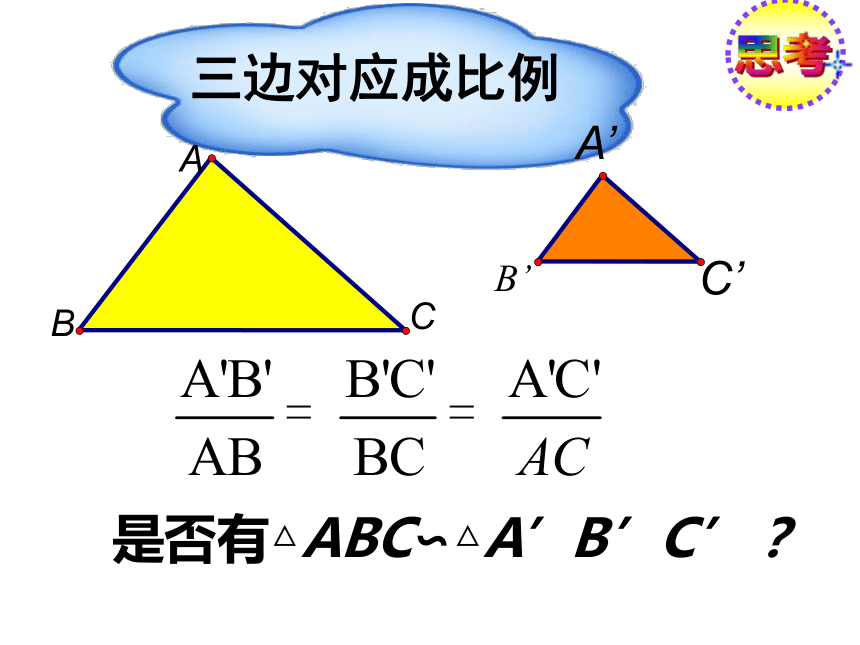
定方法呢?SSS、SAS 、ASA、AAS、HL三边对应成比例思考 是否有△ABC∽△A’B’C’?ABC已知:如图△ABC和△A`B`C`中A`B`:AB=A`C`:AC=B`C`:BC.
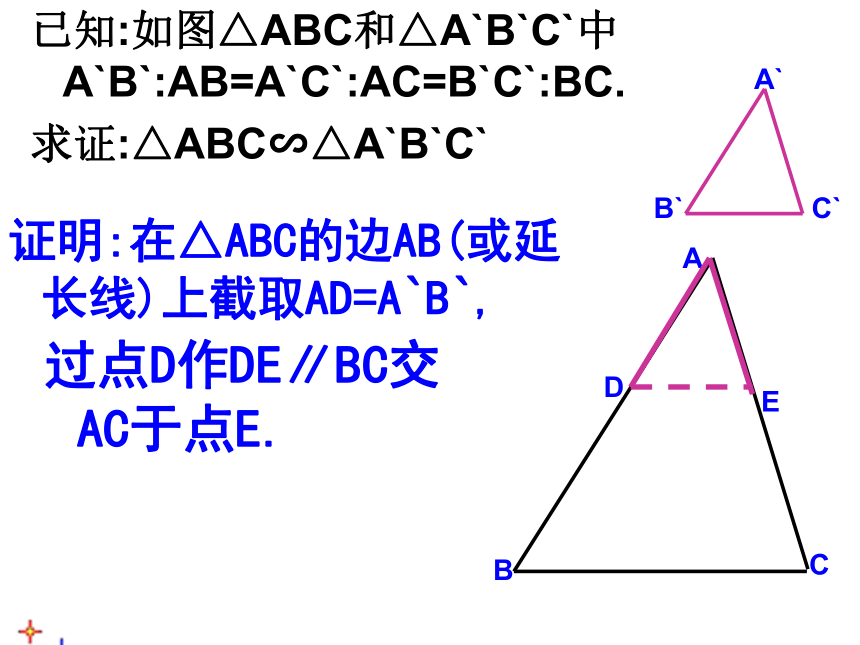
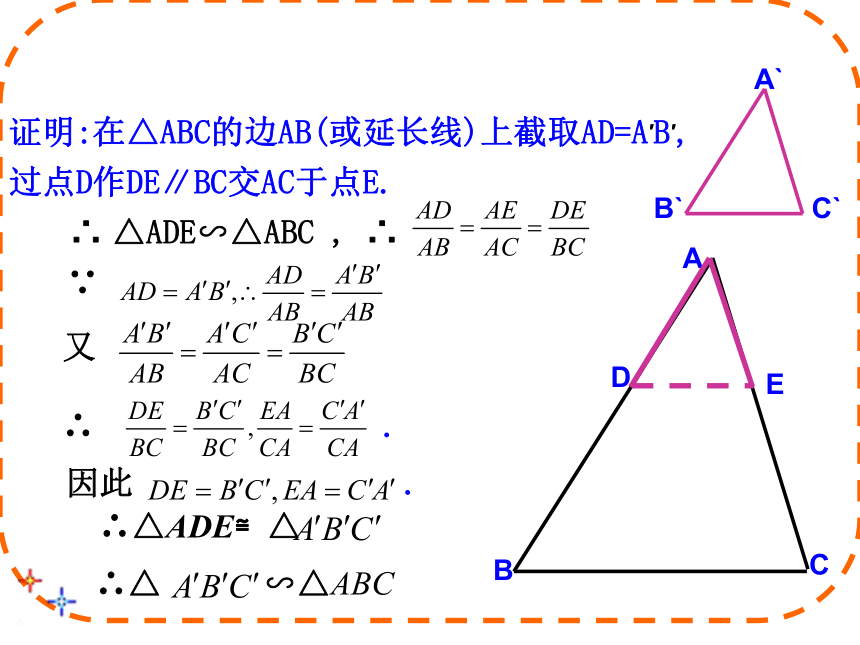
求证:△ABC∽△A`B`C`证明:在△ABC的边AB(或延长线)上截取AD=A`B`, DE过点D作DE∥BC交AC于点E.证明:在△ABC的边AB(或延长线)上截取AD=A′B′, DE过点D作DE∥BC交AC于点E. 又 ∴ △ADE∽△ABC , ∴∵ ∴ .因此 .∴△ ∽△ABC ∴△ADE≌△△ABC∽△A’B’C’ 三边对应成比例,两三角形相似.如果一个三角形的三组对应边的比相等,那么这两个三角形相似.例1:理解练习:图中两个三角形是否相似?2693414不相似类似判定三角形全等的方法,我们能通过两边和夹角来判断两个三角形相似吗?△ABC∽△A’B’C’ 两边对应成比例,并且夹角相等,两三角形相似.如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角相似.思考? 对于△ABC和△A’B’C’, 如果,
∠B=∠B’,这两个三角形一定相似吗?
试着画画看.3.23.221.650°)例1:根据下列条件,判断△ABC与△A’B’C’是否相似,并说明理由.
(1)∠A=1200,AB=7cm,AC=14cm.
∠A’=1200,A’B’=3cm,A’C’=6cm.
(2)AB=4 cm,BC=6cm,AC=8cm,
A’B’=12cm,B’C’=18cm,A’C’=21cm.△ABC与△A’B’C‘的三组对应边的比不等,它们不相似.∽要使两三角形相似,不改变的AC长,A’C’的长应改为多少?运用3相似,相似比是2:1如图在正方形网格上有△A1B1C1和△A2B2C2,它们相似吗?如果相似,求出相似比;如果不相似,请说明理由。∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC━∠DAC=∠DAE━∠DAC
即∠BAD=∠CAE 如图已知, 试说明
∠BAD=∠CAE.ADCEB2如图,AB?AE=AD?AC,且∠1=∠2,
求证:△ABC∽△AED.3.已知:如图,P为△ABC中线AD上
的一点,且
求证:△ADC∽△CDP.理解4:2=5:x=6:y
4:x=5:2=6:y
4:x=5:y=6:2要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似?4562
? 平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似;? 两边对应成比例且夹角相等,两三角形相似.相似三角形的判定方法小结? 三边对应成比例,两三角形相似.
∵ DE∥BC
数学符号语言数学符号语言平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等 平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.在△ADE与△ABC中,
∵DE//BC,∴△ADE∽△ABC1.定义法:对应角相等,对应边的比相等的
两个三角形相似回顾如何判断两三角形是否相似? ∵ DE∥BC
∴ △ ADE ∽ △ ABC 2.平行法:平行于三角形一边的直线和其他两边(或两
边的延长线)相交,所构成的三角形与原
三角形相似。A型X型猜想? 有没有其他简单的办法判断两个三角形相似呢? 三角形全等有哪几种简单的判
定方法呢?SSS、SAS 、ASA、AAS、HL三边对应成比例思考 是否有△ABC∽△A’B’C’?ABC已知:如图△ABC和△A`B`C`中A`B`:AB=A`C`:AC=B`C`:BC.
求证:△ABC∽△A`B`C`证明:在△ABC的边AB(或延长线)上截取AD=A`B`, DE过点D作DE∥BC交AC于点E.证明:在△ABC的边AB(或延长线)上截取AD=A′B′, DE过点D作DE∥BC交AC于点E. 又 ∴ △ADE∽△ABC , ∴∵ ∴ .因此 .∴△ ∽△ABC ∴△ADE≌△△ABC∽△A’B’C’ 三边对应成比例,两三角形相似.如果一个三角形的三组对应边的比相等,那么这两个三角形相似.例1:理解练习:图中两个三角形是否相似?2693414不相似类似判定三角形全等的方法,我们能通过两边和夹角来判断两个三角形相似吗?△ABC∽△A’B’C’ 两边对应成比例,并且夹角相等,两三角形相似.如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角相似.思考? 对于△ABC和△A’B’C’, 如果,
∠B=∠B’,这两个三角形一定相似吗?
试着画画看.3.23.221.650°)例1:根据下列条件,判断△ABC与△A’B’C’是否相似,并说明理由.
(1)∠A=1200,AB=7cm,AC=14cm.
∠A’=1200,A’B’=3cm,A’C’=6cm.
(2)AB=4 cm,BC=6cm,AC=8cm,
A’B’=12cm,B’C’=18cm,A’C’=21cm.△ABC与△A’B’C‘的三组对应边的比不等,它们不相似.∽要使两三角形相似,不改变的AC长,A’C’的长应改为多少?运用3相似,相似比是2:1如图在正方形网格上有△A1B1C1和△A2B2C2,它们相似吗?如果相似,求出相似比;如果不相似,请说明理由。∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC━∠DAC=∠DAE━∠DAC
即∠BAD=∠CAE 如图已知, 试说明
∠BAD=∠CAE.ADCEB2如图,AB?AE=AD?AC,且∠1=∠2,
求证:△ABC∽△AED.3.已知:如图,P为△ABC中线AD上
的一点,且
求证:△ADC∽△CDP.理解4:2=5:x=6:y
4:x=5:2=6:y
4:x=5:y=6:2要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似?4562
? 平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似;? 两边对应成比例且夹角相等,两三角形相似.相似三角形的判定方法小结? 三边对应成比例,两三角形相似.
