人教版八年级上册15.3 分式方程(第一课时)课件(共15张PPT)
文档属性
| 名称 | 人教版八年级上册15.3 分式方程(第一课时)课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 557.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 18:24:44 | ||
图片预览






文档简介
(共15张PPT)
15.3 分式方程 (第1课时)
人教版 八年级 上册
学习目标:
1.了解分式方程的概念.
2.会用去分母的方法解可化为一元一次方程的简单
的分式方程,体会化归思想和程序化思想.
3.了解解分式方程根需要进行检验的原因.
学习重点:
利用去分母的方法解分式方程.
问题1 为了解决引言中的问题,我们得到了方程
.仔细观察这个方程,未知数的位置有什
么特点?
分式方程的概念:
分母中含有未知数
的方程叫做分式方程.
练习 下列式子中,属于分式方程的是 ,
属于整式方程的是 (填序号).
(2)
(1)
(3)
要求:
1.有方法了的同学草稿本上解此方程,
没有方法的同学看书自学课本149页,
2.根据解题过程,思考:
(1)如何把它转化为整式方程的?
(2)怎样去分母?
(3)在方程的两边乘什么样的式子才能把每个分母都约去?
(4)这样做的依据是什么?
问题2 你能试着解分式方程 吗?
解分式方程
V=6
解: 方程的两边同乘以 (30+v)(30-v),得
(30+v)(30-v)
(30+v)(30-v)
.
.
解: 方程的两边同时取倒数,得
180
180
.
.
2(30+v)=3(30-v)
v = 6
90(30-v) = 60(30+v)
分式方程
整式方程
这几种化整式方程方法都适合于其它的分式方程?
分式方程
整式方程
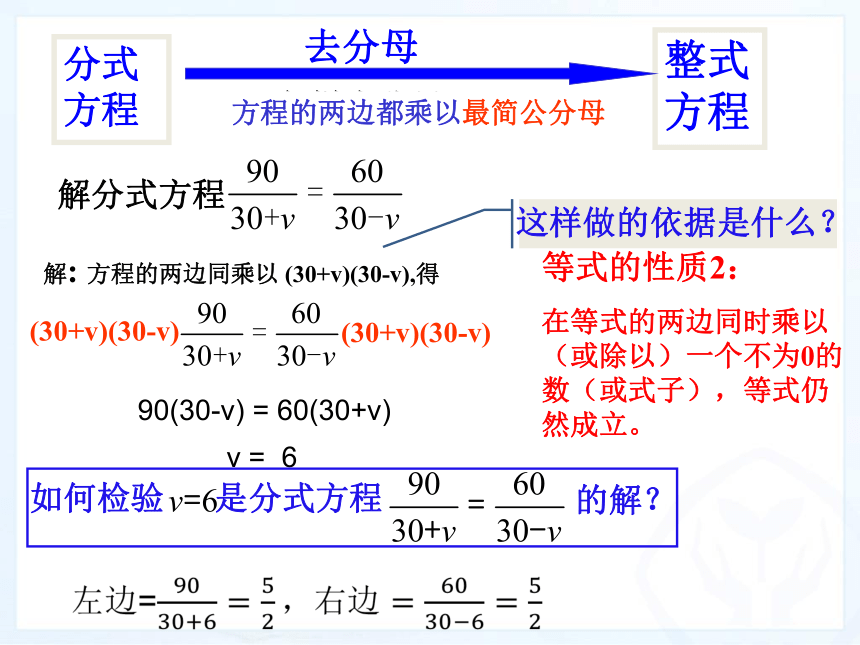
去分母
怎样去分母?
方程的两边都乘以最简公分母
解分式方程
解: 方程的两边同乘以 (30+v)(30-v),得
(30+v)(30-v)
(30+v)(30-v)
90(30-v) = 60(30+v)
这样做的依据是什么?
等式的性质2:
在等式的两边同时乘以(或除以)一个不为0的数(或式子),等式仍然成立。
v = 6
如何检验 是分式方程
的解?
问题3 解分式方程:
是原分式方程变形后的整式方程的解,但不是
原分式方程的解.
是分式方程 的解吗?
该如何验证呢?
当v=6时,(30+v)(30-v)≠0
为什么整式方程 的解 是分式方程
的解,而整式方程
的解 却不
却不是分式方程
的解?
问题4
两边同乘(x+5)(x-5)
当x=5时, (x+5)(x-5)=0
两边同乘(30+v)(30-v)
检验的方法主要有两种:
(1)将整式方程的解代入原分式方程,看左右两边是
否相等;
(2)将整式方程的解代入最简公分母,看是否为0.
解: 方程的两边同乘以 (30+v)(30-v),得
90(30-v) = 60(30+v)
解得 v = 6
检验: 当v = 6时, (30+v)(30-v)≠0
∴原分式方程的解为v = 6.
问题5 回顾解分式方程 与方程
路和一般步骤吗?
的过程,你能概括出解分式方程的基本思
基本思路:将分式方程化为整式方程
一般步骤:
(1)去分母化为整式方程;
(2)解整式方程;
(3)检验.
解: 方程的两边同乘以 (30+v)(30-v),得
90(30-v) = 60(30+v)
解得 v = 6
检验: 当v=6时, (30+v)(30-v)≠0
∴原分式方程的解为v = 6.
问题6:解分式方程应该注意什么?
例.解下列分式方程:
1.去分母时一定要找准最简公分母。
2.不要漏乘,不含分母的项也要乘。
3. 去分母后分子是一个多项式时,要把分子作为一个整体
要用括号括起来。
对比黑板上的答案:
如果答案一样则看看过程是否还需优化;
如果不一样则看看哪一步不同,是谁错了,错在哪里,为什么?
练习 解方程:
【小结】
解分式方程的一般步骤:
分式方程
整式方程
a是分式
方程的解
X=a
a不是分式
方程的解
去分母
解整式方程
检验
目标
最简公分
母不为0
最简公分
母为0
(1)本节课学习了哪些主要内容?
(2)解分式方程的基本思路和一般步骤是什么?
解分式方程应该注意什么?
布置作业
课本154页 习题15.3
1题(3)-(8)
15.3 分式方程 (第1课时)
人教版 八年级 上册
学习目标:
1.了解分式方程的概念.
2.会用去分母的方法解可化为一元一次方程的简单
的分式方程,体会化归思想和程序化思想.
3.了解解分式方程根需要进行检验的原因.
学习重点:
利用去分母的方法解分式方程.
问题1 为了解决引言中的问题,我们得到了方程
.仔细观察这个方程,未知数的位置有什
么特点?
分式方程的概念:
分母中含有未知数
的方程叫做分式方程.
练习 下列式子中,属于分式方程的是 ,
属于整式方程的是 (填序号).
(2)
(1)
(3)
要求:
1.有方法了的同学草稿本上解此方程,
没有方法的同学看书自学课本149页,
2.根据解题过程,思考:
(1)如何把它转化为整式方程的?
(2)怎样去分母?
(3)在方程的两边乘什么样的式子才能把每个分母都约去?
(4)这样做的依据是什么?
问题2 你能试着解分式方程 吗?
解分式方程
V=6
解: 方程的两边同乘以 (30+v)(30-v),得
(30+v)(30-v)
(30+v)(30-v)
.
.
解: 方程的两边同时取倒数,得
180
180
.
.
2(30+v)=3(30-v)
v = 6
90(30-v) = 60(30+v)
分式方程
整式方程
这几种化整式方程方法都适合于其它的分式方程?
分式方程
整式方程
去分母
怎样去分母?
方程的两边都乘以最简公分母
解分式方程
解: 方程的两边同乘以 (30+v)(30-v),得
(30+v)(30-v)
(30+v)(30-v)
90(30-v) = 60(30+v)
这样做的依据是什么?
等式的性质2:
在等式的两边同时乘以(或除以)一个不为0的数(或式子),等式仍然成立。
v = 6
如何检验 是分式方程
的解?
问题3 解分式方程:
是原分式方程变形后的整式方程的解,但不是
原分式方程的解.
是分式方程 的解吗?
该如何验证呢?
当v=6时,(30+v)(30-v)≠0
为什么整式方程 的解 是分式方程
的解,而整式方程
的解 却不
却不是分式方程
的解?
问题4
两边同乘(x+5)(x-5)
当x=5时, (x+5)(x-5)=0
两边同乘(30+v)(30-v)
检验的方法主要有两种:
(1)将整式方程的解代入原分式方程,看左右两边是
否相等;
(2)将整式方程的解代入最简公分母,看是否为0.
解: 方程的两边同乘以 (30+v)(30-v),得
90(30-v) = 60(30+v)
解得 v = 6
检验: 当v = 6时, (30+v)(30-v)≠0
∴原分式方程的解为v = 6.
问题5 回顾解分式方程 与方程
路和一般步骤吗?
的过程,你能概括出解分式方程的基本思
基本思路:将分式方程化为整式方程
一般步骤:
(1)去分母化为整式方程;
(2)解整式方程;
(3)检验.
解: 方程的两边同乘以 (30+v)(30-v),得
90(30-v) = 60(30+v)
解得 v = 6
检验: 当v=6时, (30+v)(30-v)≠0
∴原分式方程的解为v = 6.
问题6:解分式方程应该注意什么?
例.解下列分式方程:
1.去分母时一定要找准最简公分母。
2.不要漏乘,不含分母的项也要乘。
3. 去分母后分子是一个多项式时,要把分子作为一个整体
要用括号括起来。
对比黑板上的答案:
如果答案一样则看看过程是否还需优化;
如果不一样则看看哪一步不同,是谁错了,错在哪里,为什么?
练习 解方程:
【小结】
解分式方程的一般步骤:
分式方程
整式方程
a是分式
方程的解
X=a
a不是分式
方程的解
去分母
解整式方程
检验
目标
最简公分
母不为0
最简公分
母为0
(1)本节课学习了哪些主要内容?
(2)解分式方程的基本思路和一般步骤是什么?
解分式方程应该注意什么?
布置作业
课本154页 习题15.3
1题(3)-(8)
