沪科版八年级上册 12.2.2正比例函数图像及其性质 课件(共20张PPT)
文档属性
| 名称 | 沪科版八年级上册 12.2.2正比例函数图像及其性质 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
12.2 一次函数
第1课时 正比例函数的图象和性质
情境创设:电信公司推出市话服务,收费标准为月租费15元,本地网通话费为每分钟0.1元。
(1)完成下表:
(2)你能写出y与x的函数关系式吗
y=15+0.1x
X(分钟)
1
2 3 4 ….
通话费用(元)
…
应缴费用Y(元) …
0.1
0.2
0.3
0.4
15.1
15.2
15.3
15.4
观察下列函数关系式有什么共同的特点
(1) h=30t+1800
(3) y=15+0.1x
(2) Q=-25t+300
1、函数解析式都是整式表达式
2、自变量的次数都是一次
(4)S=80t
(5)y=2x
(6)y=-2x
y=kx+b(k≠0)
当b=0时,一次函数y=kx+b就成为y=kx
(k为常数,且k≠0)
一般地,形如y=kx+b(k、b为常数,k≠0)的函数,叫做一次函数。
正比例函数是一次函数,它是一次函数的特殊情形
因此,形如y=kx(k为常数,且k≠0)的函数叫做正比例函数
每人写一个一次函数,请同桌指出其中k、b的值。
示例:y=-3x+2
(k=____ b =____ )
小试牛刀:下列函数关系式中,哪些是一次函数,哪些是正比例函数?
(1)y=-x-4
(2)y=5x2+6
(3)y=2πx
(5)y=-8x
(4)
(6)y=2(t-5)
(1), (3), (5), (6)是一次函数
(3), (5), 是正比例函数
-6
-5
-4
-3
-2
-1
0
5
4
3
2
1
-1
-2
-3
-4
-5
1
2
3
4
5
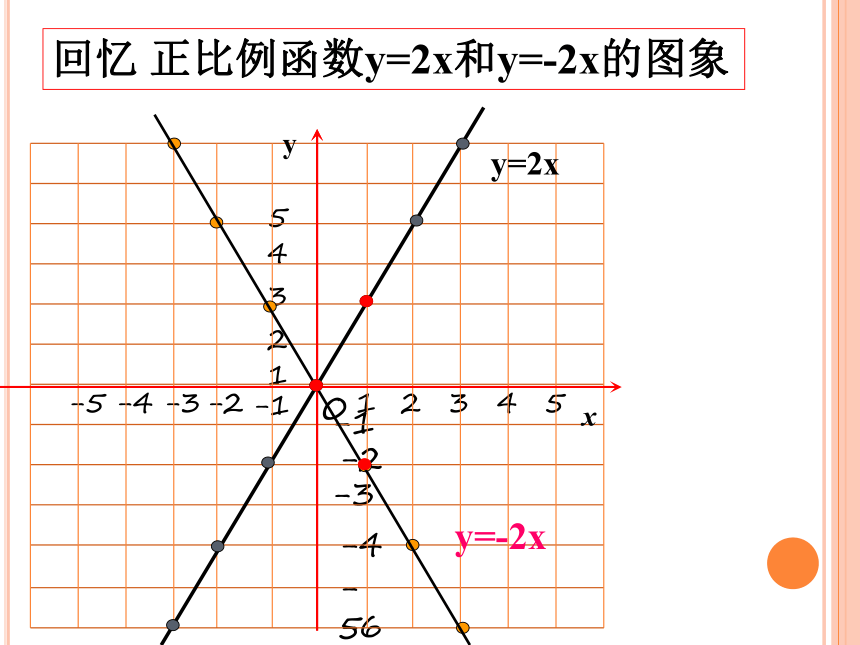
回忆 正比例函数y=2x和y=-2x的图象
x
y
y=2x
y=-2x
(1)正比例函数y=kx (k≠0)的图象有什么特点?
正比例函数y=kx(k≠0)的图象是经过原点(0,0)的一条直线
(2)现在作正比例函数y=kx的图象时只需描几个点?
作y=kx(k≠0)的图象时,除原点外还需找一点。
因此,正比例函数的图像是一条经过(0,0)以及(1,k)的直线
最好选择点(1,K)
通常我们把y=kx(k为常数,且不等于0)的图象叫做直线y=kx
例1 在同一平面直角坐标系中画出下列函数的图象
解:列表:
x … 0 1 …
… 0 …
y=x … 0 1 …
y=3x … 0 3 …
过两点(0、0),(1、1/2)画直线 的图象;
过两点(0、0),(1、1)画直线,得y=x的图象。
过两点(0、0),(1、3)画直线,得y=3x的图象
1
y
x
o
图像从左到右呈上升趋势,y随x 的增大而增大,经过一、三象限
3
3
1
看一看:下面图像的自左向右的变化趋势
以及所经过的象限
1
y
x
o
在同一坐标系内画下列正比例函数的图像:
图像从左到右呈下降趋势,y随x 的增大而减小,经过二、四象限
看一看:下面图像的自左向右的变化趋势:
K的符号 经过点 经过象限 图象 图象变化趋势 y随x的变化情况
k>0
(0,0)
一、三象限 y
0
x
从左向右呈上升趋势
y随着x的增大而增大
k<0
(0,0)
二、四象限
0 x
从左向右呈下降趋势
y随着x的增大而减小
y
正比例函数的图象及性质
抢答:看谁反应快
1.由函数解析式,请你说出下列函数的y随x的变化情况
y随x的增大而增大
y随x的增大而增大
y随x的增大而减小
2.下列图像哪个可能是函数y=-8x的图像( )
A B C D
B
y
y
y
y
x
x
x
x
3. 如图是正比例函数y=(m-2)x的图像,试求m的取值范围( )
A、m>0 B、m<2 C、m>2 D、m<0
B
x
y
O
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
x
y
O
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
x
y
看一看,下列函数图像那些离y轴更近,与k的值有何关系?
当k>0时,
k越大函数越靠近y轴
当k<0时,
k越小函数越靠近y轴
当 | k | 越大时,
图像越靠近y轴
如图,三个正比例函数的图像分别对应的解析式是 ①y=ax② y=bx ③ y=cx,则a、b、c的大小关系是( )
A.a>b>c B.c>b>a
C.b>a>c D.b>c>a
练习
x
y
①
②
③
C
提示训练
3.函数y=-7x的图象在第_________象限内,经过点_______
与点 ,y随x的增大而__________.
二、四
(0,0)
(1,-7)
减小
4.正比例函数y=(k+1)x的图象中y随x的增大而增大,则k的取值范围是____________.
k>-1
1.正比例函数y=(m-1)x的图象经过第一、三象限,则m的
取值范围是( )
A.m=1 B.m>1 C.m<1 D.m≥1
B
2.若y=5x3m-2 是正比例函数,则m= .
1
经历今天的学习活动,你有何收获和体会?
12.2 一次函数
第1课时 正比例函数的图象和性质
情境创设:电信公司推出市话服务,收费标准为月租费15元,本地网通话费为每分钟0.1元。
(1)完成下表:
(2)你能写出y与x的函数关系式吗
y=15+0.1x
X(分钟)
1
2 3 4 ….
通话费用(元)
…
应缴费用Y(元) …
0.1
0.2
0.3
0.4
15.1
15.2
15.3
15.4
观察下列函数关系式有什么共同的特点
(1) h=30t+1800
(3) y=15+0.1x
(2) Q=-25t+300
1、函数解析式都是整式表达式
2、自变量的次数都是一次
(4)S=80t
(5)y=2x
(6)y=-2x
y=kx+b(k≠0)
当b=0时,一次函数y=kx+b就成为y=kx
(k为常数,且k≠0)
一般地,形如y=kx+b(k、b为常数,k≠0)的函数,叫做一次函数。
正比例函数是一次函数,它是一次函数的特殊情形
因此,形如y=kx(k为常数,且k≠0)的函数叫做正比例函数
每人写一个一次函数,请同桌指出其中k、b的值。
示例:y=-3x+2
(k=____ b =____ )
小试牛刀:下列函数关系式中,哪些是一次函数,哪些是正比例函数?
(1)y=-x-4
(2)y=5x2+6
(3)y=2πx
(5)y=-8x
(4)
(6)y=2(t-5)
(1), (3), (5), (6)是一次函数
(3), (5), 是正比例函数
-6
-5
-4
-3
-2
-1
0
5
4
3
2
1
-1
-2
-3
-4
-5
1
2
3
4
5
回忆 正比例函数y=2x和y=-2x的图象
x
y
y=2x
y=-2x
(1)正比例函数y=kx (k≠0)的图象有什么特点?
正比例函数y=kx(k≠0)的图象是经过原点(0,0)的一条直线
(2)现在作正比例函数y=kx的图象时只需描几个点?
作y=kx(k≠0)的图象时,除原点外还需找一点。
因此,正比例函数的图像是一条经过(0,0)以及(1,k)的直线
最好选择点(1,K)
通常我们把y=kx(k为常数,且不等于0)的图象叫做直线y=kx
例1 在同一平面直角坐标系中画出下列函数的图象
解:列表:
x … 0 1 …
… 0 …
y=x … 0 1 …
y=3x … 0 3 …
过两点(0、0),(1、1/2)画直线 的图象;
过两点(0、0),(1、1)画直线,得y=x的图象。
过两点(0、0),(1、3)画直线,得y=3x的图象
1
y
x
o
图像从左到右呈上升趋势,y随x 的增大而增大,经过一、三象限
3
3
1
看一看:下面图像的自左向右的变化趋势
以及所经过的象限
1
y
x
o
在同一坐标系内画下列正比例函数的图像:
图像从左到右呈下降趋势,y随x 的增大而减小,经过二、四象限
看一看:下面图像的自左向右的变化趋势:
K的符号 经过点 经过象限 图象 图象变化趋势 y随x的变化情况
k>0
(0,0)
一、三象限 y
0
x
从左向右呈上升趋势
y随着x的增大而增大
k<0
(0,0)
二、四象限
0 x
从左向右呈下降趋势
y随着x的增大而减小
y
正比例函数的图象及性质
抢答:看谁反应快
1.由函数解析式,请你说出下列函数的y随x的变化情况
y随x的增大而增大
y随x的增大而增大
y随x的增大而减小
2.下列图像哪个可能是函数y=-8x的图像( )
A B C D
B
y
y
y
y
x
x
x
x
3. 如图是正比例函数y=(m-2)x的图像,试求m的取值范围( )
A、m>0 B、m<2 C、m>2 D、m<0
B
x
y
O
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
x
y
O
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
x
y
看一看,下列函数图像那些离y轴更近,与k的值有何关系?
当k>0时,
k越大函数越靠近y轴
当k<0时,
k越小函数越靠近y轴
当 | k | 越大时,
图像越靠近y轴
如图,三个正比例函数的图像分别对应的解析式是 ①y=ax② y=bx ③ y=cx,则a、b、c的大小关系是( )
A.a>b>c B.c>b>a
C.b>a>c D.b>c>a
练习
x
y
①
②
③
C
提示训练
3.函数y=-7x的图象在第_________象限内,经过点_______
与点 ,y随x的增大而__________.
二、四
(0,0)
(1,-7)
减小
4.正比例函数y=(k+1)x的图象中y随x的增大而增大,则k的取值范围是____________.
k>-1
1.正比例函数y=(m-1)x的图象经过第一、三象限,则m的
取值范围是( )
A.m=1 B.m>1 C.m<1 D.m≥1
B
2.若y=5x3m-2 是正比例函数,则m= .
1
经历今天的学习活动,你有何收获和体会?
