沪科版八年级上册12.2.3一次函数的图象与性质 课件(共17张PPT)
文档属性
| 名称 | 沪科版八年级上册12.2.3一次函数的图象与性质 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 18:40:37 | ||
图片预览




文档简介
(共17张PPT)
复习引入
函数是刻画某一变化过程中两个变量之间的一种特定关系。
12.2(第3课时)
一次函数的性质
1
y=2x-3
0
x
y=3x+1
y=0.5x+4
-3
-2
-1
2
3
4
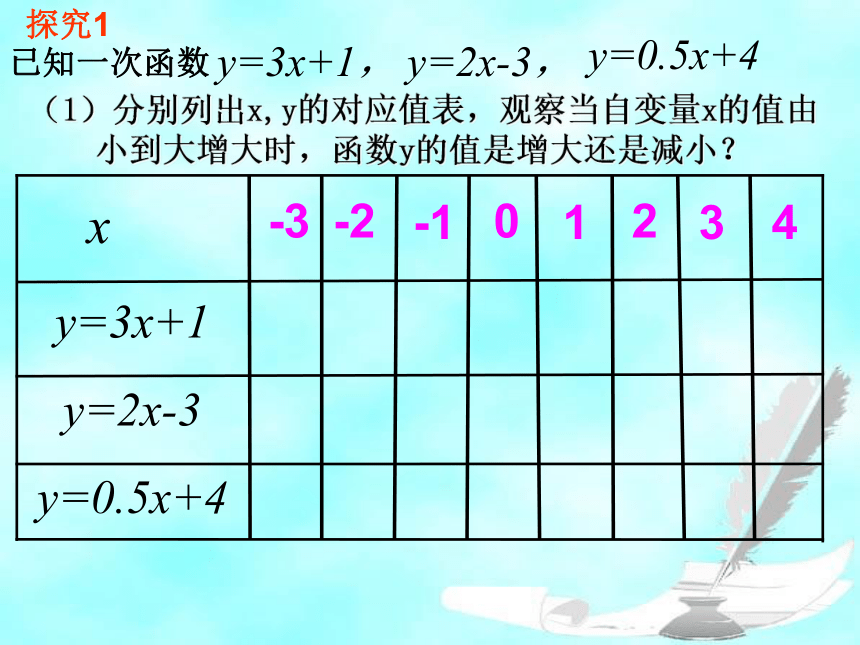
探究1
已知一次函数
y=3x+1,
y=2x-3,
y=0.5x+4
(1)分别列出x,y的对应值表,观察当自变量x的值由小到大增大时,函数y的值是增大还是减小?
1
y=2x-3
0
x
y=3x+1
y=0.5x+4
-3
-2
-1
2
3
4
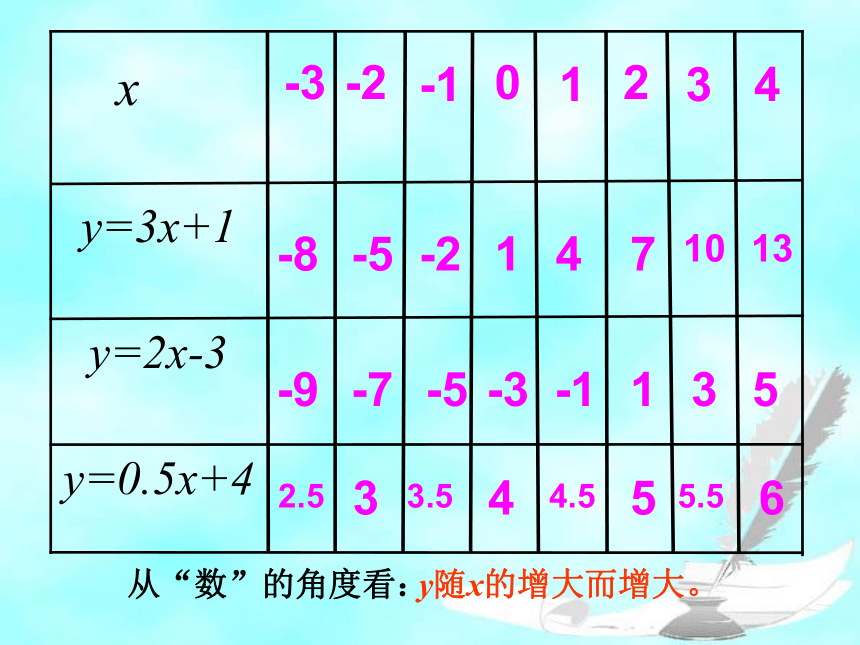
-8
-5
-2
1
4
7
10
13
-9
-7
-5
-3
-1
1
3
5
2.5
3
3.5
4
4.5
5
5.5
6
从“数”的角度看:
y随x的增大而增大。
1
y=2x-3
0
x
y=3x+1
y=0.5x+4
-3
-2
-1
2
3
4
-8
-5
-2
1
4
7
10
13
-9
-7
-5
-3
-1
1
3
5
2.5
3
3.5
4
4.5
5
5.5
6
想象:
“数”的变化规律会不会在“形”上有所反映呢
(2)分别画出y=3x+1,y=2x-3,y=0.5x+4
的图象,上述变化从图象上看,直线从左到右是上升还是下降?(点击)
(3)K>0时,任意一个一次函数y=kx+b,从图象上看:从左到右会不会都呈上升趋势呢?(点击)
K>0时,函数y=kx+b的图象从左到右上升;
1
y=-2x+3
0
x
y=-3x-1
y=-0.5x-4
-3
-2
-1
2
3
4
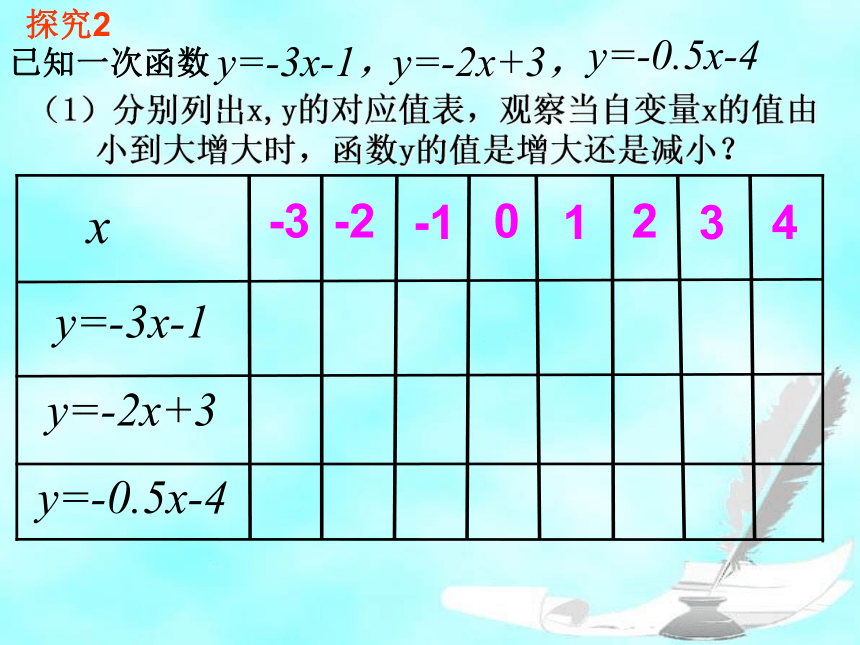
探究2
已知一次函数
y=-3x-1,
y=-2x+3,
y=-0.5x-4
(1)分别列出x,y的对应值表,观察当自变量x的值由小到大增大时,函数y的值是增大还是减小?
1
y=-2x+3
0
x
y=-3x-1
y=-0.5x-4
-3
-2
-1
2
3
4
8
5
2
-1
-4
-7
-10
-13
9
7
5
3
1
-1
-3
-5
-2.5
-3
-3.5
-4
-4.5
-5
-5.5
-6
从“数”的角度看:
y随x的增大而减小。
1
y=-2x+3
0
x
y=-3x-1
y=-0.5x-4
-3
-2
-1
2
3
4
8
5
2
-1
-4
-7
-10
-13
9
7
5
3
1
-1
-3
-5
-2.5
-3
-3.5
-4
-4.5
-5
-5.5
-6
想象:
“数”的变化规律会不会在“形”上有所反映呢
(2)分别画出y=-3x-1,y=-2x+3,y=-0.5x-4
的图象,观察直线从左到右是上升还是下降?(点击)
(3)K<0时,任意一个一次函数y=kx+b,从图象上看:从左到右会不会都呈下降趋势呢?(点击)
K<0时,函数y=kx+b的图象从左到右下降;
概括
一次函数y=kx+b有下列性质:
(1) 当k>0时,y随x的增大而_____ ,这时函数的图象从左到右_____ ;
(2) 当k <0时, y随x的增大而_____,这时函数的图象从左到右_____.
减小
下降
增大
上升
K,b对一次函数y=kx+b的图象影响(点击)
深化
课堂剧场
从前,有个叫一次函数y=kx+b的家庭中,有四个家庭成员:因变量y,自变量x,系数小K,截距小b。
X:(盛气凌人)y,我变大,你也变大,我变小,你也跟着变小,太没个性了吧?
y:(脸微微一红)谁让你是我的偶象呢?我的神,我与你的变化趋势超级一致,能随着你的变化节奏起舞,我无尚荣幸啊!
X:(歉意又得意)谁知道俺也有粉丝呢?呵呵、、、
一天,k>0时
y与时俱进,很潮。
X:(不满)y,我变大,你却变小,我变小,你却变大,你咋老跟我呛呢?
y:(不以为然)谁叫我正在青春期呢?粉丝难当,哼,叛逆、反抗才是我。
X:(无可耐何)唉,真拿你没办法。
又一天,k〈0时
y叛逆,具有反抗精神,活得有个性。
1.填空:
(1) 对于函数 y = 7x, y 随 x 的 而增大;
增大
(2) 对于函数 y = –2x + 3 , y 随 x 的增大而
减小
课堂练习
已知一次函数 y = ( 2m - 4) x -5,(1)若 y 随 x 的增大而增大,求 m 的取值范围;(2)若直线y = ( 2m - 4) x -5从左向右下降,求 m 的取值范围.
例1
例2 某商场计划购进男、女式两款冬季流行装共100件,男式装进价300元,售价700元;女式装进价200元,售价800元。若女式装的进货量不超过男式装的4倍,男装应进多少件才能使商场售完这批服装时获利最多?最大利润为多少?
复习引入
函数是刻画某一变化过程中两个变量之间的一种特定关系。
12.2(第3课时)
一次函数的性质
1
y=2x-3
0
x
y=3x+1
y=0.5x+4
-3
-2
-1
2
3
4
探究1
已知一次函数
y=3x+1,
y=2x-3,
y=0.5x+4
(1)分别列出x,y的对应值表,观察当自变量x的值由小到大增大时,函数y的值是增大还是减小?
1
y=2x-3
0
x
y=3x+1
y=0.5x+4
-3
-2
-1
2
3
4
-8
-5
-2
1
4
7
10
13
-9
-7
-5
-3
-1
1
3
5
2.5
3
3.5
4
4.5
5
5.5
6
从“数”的角度看:
y随x的增大而增大。
1
y=2x-3
0
x
y=3x+1
y=0.5x+4
-3
-2
-1
2
3
4
-8
-5
-2
1
4
7
10
13
-9
-7
-5
-3
-1
1
3
5
2.5
3
3.5
4
4.5
5
5.5
6
想象:
“数”的变化规律会不会在“形”上有所反映呢
(2)分别画出y=3x+1,y=2x-3,y=0.5x+4
的图象,上述变化从图象上看,直线从左到右是上升还是下降?(点击)
(3)K>0时,任意一个一次函数y=kx+b,从图象上看:从左到右会不会都呈上升趋势呢?(点击)
K>0时,函数y=kx+b的图象从左到右上升;
1
y=-2x+3
0
x
y=-3x-1
y=-0.5x-4
-3
-2
-1
2
3
4
探究2
已知一次函数
y=-3x-1,
y=-2x+3,
y=-0.5x-4
(1)分别列出x,y的对应值表,观察当自变量x的值由小到大增大时,函数y的值是增大还是减小?
1
y=-2x+3
0
x
y=-3x-1
y=-0.5x-4
-3
-2
-1
2
3
4
8
5
2
-1
-4
-7
-10
-13
9
7
5
3
1
-1
-3
-5
-2.5
-3
-3.5
-4
-4.5
-5
-5.5
-6
从“数”的角度看:
y随x的增大而减小。
1
y=-2x+3
0
x
y=-3x-1
y=-0.5x-4
-3
-2
-1
2
3
4
8
5
2
-1
-4
-7
-10
-13
9
7
5
3
1
-1
-3
-5
-2.5
-3
-3.5
-4
-4.5
-5
-5.5
-6
想象:
“数”的变化规律会不会在“形”上有所反映呢
(2)分别画出y=-3x-1,y=-2x+3,y=-0.5x-4
的图象,观察直线从左到右是上升还是下降?(点击)
(3)K<0时,任意一个一次函数y=kx+b,从图象上看:从左到右会不会都呈下降趋势呢?(点击)
K<0时,函数y=kx+b的图象从左到右下降;
概括
一次函数y=kx+b有下列性质:
(1) 当k>0时,y随x的增大而_____ ,这时函数的图象从左到右_____ ;
(2) 当k <0时, y随x的增大而_____,这时函数的图象从左到右_____.
减小
下降
增大
上升
K,b对一次函数y=kx+b的图象影响(点击)
深化
课堂剧场
从前,有个叫一次函数y=kx+b的家庭中,有四个家庭成员:因变量y,自变量x,系数小K,截距小b。
X:(盛气凌人)y,我变大,你也变大,我变小,你也跟着变小,太没个性了吧?
y:(脸微微一红)谁让你是我的偶象呢?我的神,我与你的变化趋势超级一致,能随着你的变化节奏起舞,我无尚荣幸啊!
X:(歉意又得意)谁知道俺也有粉丝呢?呵呵、、、
一天,k>0时
y与时俱进,很潮。
X:(不满)y,我变大,你却变小,我变小,你却变大,你咋老跟我呛呢?
y:(不以为然)谁叫我正在青春期呢?粉丝难当,哼,叛逆、反抗才是我。
X:(无可耐何)唉,真拿你没办法。
又一天,k〈0时
y叛逆,具有反抗精神,活得有个性。
1.填空:
(1) 对于函数 y = 7x, y 随 x 的 而增大;
增大
(2) 对于函数 y = –2x + 3 , y 随 x 的增大而
减小
课堂练习
已知一次函数 y = ( 2m - 4) x -5,(1)若 y 随 x 的增大而增大,求 m 的取值范围;(2)若直线y = ( 2m - 4) x -5从左向右下降,求 m 的取值范围.
例1
例2 某商场计划购进男、女式两款冬季流行装共100件,男式装进价300元,售价700元;女式装进价200元,售价800元。若女式装的进货量不超过男式装的4倍,男装应进多少件才能使商场售完这批服装时获利最多?最大利润为多少?
